단방향 압축함수

암호학에서 단방향 압축함수는 두 개의 고정 길이 입력을 고정 길이 출력으로 변환하는 함수다.^[1]변환은 "일방향"으로, 즉 특정 출력으로 압축되는 입력을 계산하는 것이 어렵다는 것을 의미한다.단방향 압축 함수는 기존의 데이터 압축 알고리즘과는 관련이 없으며, 대신 원본 데이터에 대해 정확하게 반전(무손실 압축)하거나 대략적으로(손실 압축)할 수 있다.

단방향 압축 함수

단방향 압축함수는 예를 들어 암호해시함수 내부의 Merkle-Damgård 구성에 사용된다.

단방향 압축 기능은 블록 암호로 구축되는 경우가 많다.일반적인 블록 암호를 단방향 압축 함수로 변환하는 몇 가지 방법은 Davies이다.–마이어, 마타야스–Meyer-Oseas, 미야구치-프레넬(단일 블록 길이 압축 함수) 및 MDC-2/Meyer-Schilling, MDC-4, Hirose(이중 블록 길이 압축 함수)이 방법들은 더 아래에 자세히 설명되어 있다. (MDC-2는 IBM이 특허를 받은 해시함수의 명칭이기도 하다.)

압축

압축 함수는 두 개의 고정 길이 입력을 혼합하고 입력 중 하나와 동일한 크기의 고정 길이 출력을 단일 생성한다.이는 압축함수가 하나의 큰 고정 길이 입력을 보다 짧은 고정 길이 출력으로 변환하는 것으로도 볼 수 있다.

예를 들어, 입력 A는 128비트, 입력 B 128비트가 될 수 있으며 128비트의 단일 출력으로 압축된다.이는 단일 256비트 입력을 128비트의 단일 출력으로 압축한 것과 맞먹는다.

일부 압축 함수는 절반으로 압축하지 않고 다른 일부 인자에 의해 압축된다.예를 들어 입력 A는 256비트, 입력 B 128비트는 128비트의 단일 출력으로 압축될 수 있다.즉, 총 384개의 입력 비트가 128개의 출력 비트로 압축된다.

혼합은 완전한 눈사태 효과를 얻을 수 있는 방식으로 이루어진다.즉, 모든 출력 비트는 모든 입력 비트에 따라 달라진다.

일방통행

단방향 함수는 계산은 쉽지만 뒤집기는 어려운 함수다.단방향 압축함수(해시함수라고도 함)는 다음과 같은 속성을 가져야 한다.

계산하기 쉬운:일부 입력이 있으면 출력을 계산하기 쉽다.
사전 이미지 저항:공격자가 출력만 알면 입력을 계산할 수 없다.즉, 출력 $h$ ${\displaystyle$ $h$ $}$ 을 $h$ 를) 지정하면 $\operatorname {hash} (m)=h$ $\operatorname {hash} (m)=h$ $\operatorname {hash} (m)=h$ = $\operatorname {hash} (m)=h$ $\operatorname {hash}(m)=h$ 과 $m$ 같은 입력 $m$ ${\displaystym$ m}을 $($ 를) 계산하는 것이 불가능해야 한다 $\operatorname {hash} (m)=h$
Second preimage-resistance: Given an input $m_{1}$ whose output is $h$ , it should be infeasible to find another input $m_{2}$ that has the same output $h$ , i.e. $\operatorname {hash$ $(m_{1}}\neq \computname {filename}(m_{2})}$ .
충돌 저항:It should be hard to find any two different inputs that compress to the same output i.e. an attacker should not be able to find a pair of messages $m_{1}\neq m_{2}$ such that $\operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})$ . Due to the생일 역설(생일 공격 참조)은 약 $2^{n/2}$ / 2 ${\$ 2 $^{n/2}}$ 시에 충돌이 발견될 확률이 50%이며, 여기서 $2^{n/2}$ $n$ $n$ 은 $n$ 해시함수의 출력에 있는 비트 수입니다.따라서 해시함수에 대한 공격은 약 $2^{n/2}$ / $2^{n/2}$ ${\$ 개 $2^{n/2}$ 이하의 작업과 충돌을 발견할 수 없어야 한다.

이상적으로는 프리이미지 저항성 및 두 번째 프리이미지 저항성의 "무효성"이 $2^{n}$ 2n ${\$ 의 $2^{n}$ 을 의미하기를 원하며, 여기서 $2^{n}$ $n$ $n$ 은 $n$ 해시함수의 출력에 있는 비트 수입니다.그러나 특히 두 번째 사전 이미지 저항의 경우 이것은 어려운 문제다.^{[citation needed]}

머클-담그드 건설

Merkle-Damghrd 해시 건설.[f]라고 표시된 상자는 단방향 압축함수다.

단방향 압축함수의 공통적인 용도는 암호해시함수 내부의 Merkle-Damgrdrd 구조에 있다.MD5, SHA-1(사용불가^[2]) 및 SHA-2를 포함하여 가장 널리 사용되는 해시함수는 이 구성을 사용한다.

해시함수는 임의 길이 메시지를 고정 길이 출력으로 처리할 수 있어야 한다.이는 입력을 일련의 동일한 크기의 블록으로 세분화하여 단방향 압축 함수를 사용하여 순차적으로 작동함으로써 달성할 수 있다.압축함수는 해싱을 위해 특별히 설계하거나 블록 암호로 제작할 수 있다.

마지막으로 처리된 블록은 길이 패딩도 해야 하며, 이는 이 공사의 보안에 매우 중요하다.이 공사는 메르클-담그드 건설이라고 불린다.SHA-1과 MD5를 포함하여 가장 널리 사용되는 해시함수는 이 형식을 취한다.

길이 패딩(MD 강화라고도 함)^[3]^[4]을 적용할 때 사용된 함수 $f$ $f$ 이(가) 충돌에 내성이 있으면 $f$ 생일 역설( $2^{n/2}$ / 2 ${\$ 2 $^{n/2$ $n$ ${\displaystyn}$ 이(비트 단위 블록 크기임 $n$ )보다 공격이 더 빠른 충돌을 찾을 수 없다.따라서 Merkle-Damgård 해시구축은 적절한 해시함수를 찾는 문제를 적절한 압축함수를 찾는 문제로 줄인다.

두번째 preimage 공격(메시지를 m1{\displaystyle m_{1}}를 주어진 공격자를 찾는다 다른 메세지를 m2{\displaystyle m_{2}}각각 충족 해시 ⁡(m1))hash ⁡(m2){\displaystyle \operatorname{해시}(m_{1})=\operatorname{해시}(m_{2})}이 될 수 있는 일에 따르면 켈시와 Schneier[5]에 대한 2k. ${\displaystyle 2^{k}}-$ block $2^{k}$ $k\times 2^{n/2+1}+2^{n-k+1}$ in $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ / $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 + $k\times 2^{n/2+1}+2^{n-k+1}$ - $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 ${\$ 2^{ $n/2+1}+2^{n-k+$ 1}:{n-k+1}:{n-k $+$ 1}:{n2 $k\times 2^{n/2+1}+2^{n-k+1}$ $k=2^{n/4}$ 공격의 복잡성은 $k=2^{n/4}$ = $k=2^{n/4}$ $k=2^{n/4}$ $2^{3n/4+2}$ + 2 ${\$ 긴 메시지에 대해 $2^{3n/4+2}$ 최소 $2^{3n/4+2}$ $2^{3n/4+2}$ / 4 ${\$ 메시지가 $k=2^{n/4}$ 짧을 $2^{n}$ 때 $2^{n}$ ${\$ 에 근접한다는 점에 유의하십시오.

블록 암호로부터의 구조

전형적인 현대 블록 암호

단방향 압축 기능은 블록 암호로 구축되는 경우가 많다.

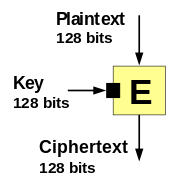
블록 암호는 (일방향 압축함수와 마찬가지로) 두 개의 고정 크기 입력(키와 일반 텍스트)을 취하여 입력 일반 텍스트와 동일한 크기의 단일 출력(암호 텍스트)을 반환한다.

그러나 현대의 블록 암호는 부분적으로 단방향일 뿐이다.즉, 일반 텍스트와 암호 텍스트에 따라 암호 텍스트에 대한 일반 텍스트를 암호화하는 키를 찾는 것은 불가능하다.그러나 암호문 및 키에 따라 일치하는 일반 텍스트는 블록 암호의 암호 해독 기능을 사용하여 간단히 찾을 수 있다.그러므로 블록 암호를 단방향 압축 함수로 바꾸려면 일부 추가 연산을 추가해야 한다.

일반적인 블록 암호를 단방향 압축 함수로 변환하는 몇 가지 방법은 Davies이다.–마이어, 마타야스–Meyer-Oseas, 미야구치-프레넬(단일 블록 길이 압축 함수) 및 MDC-2, MDC-4, Hirose(이중 블록 길이 압축 함수)

단일 블록 길이 압축 함수는 기본 블록 암호에 의해 처리된 것과 동일한 수의 비트를 출력한다.따라서 이중 블록 길이 압축 함수는 비트 수의 두 배를 출력한다.

블록 암호의 블록 크기가 say 128비트 단일 블록 길이 방법인 경우 블록 크기가 128비트인 해시 함수를 생성하고 128비트의 해시를 생성한다.더블 블록 길이 방법은 사용하는 블록 암호의 블록 크기에 비해 해시 크기가 두 배나 되는 해시를 만든다.그래서 128비트 블록 암호는 256비트 해시함수로 바꿀 수 있다.

이후 Merkle-Damghrd 구조 내부에 이러한 방법을 사용하여 실제 해시함수를 구축한다.이 방법들은 좀 더 아래에 자세히 설명되어 있다.

해시함수에 대한 단방향 압축함수를 구축하기 위해 블록 암호를 사용하는 것은 해시함수에 특별히 설계된 단방향 압축함수를 사용하는 것보다 보통 다소 느리다.이는 알려진 모든 보안 구성 요소가 메시지의 각 블록에 대해 키 스케줄링을 수행하기 때문이다.블랙, 코크란, 슈림프턴은 고정된 키로 블록 암호에 한 통화만 하는 단방향 압축함수를 구성하는 것이 불가능하다는 것을 보여주었다.^[6]실제로 선택된 블록 암호의 키 스케줄링이 너무 무거운 작업이 아니라면 합리적인 속도가 달성된다.

그러나 어떤 경우에는 블록 암호의 단일 구현이 블록 암호와 해시함수 모두에 사용될 수 있기 때문에 더 쉽다.그것은 또한 스마트 카드나 자동차나 다른 기계들의 노드나 같은 아주 작은 임베디드 시스템의 코드 공간을 절약할 수 있다.

따라서 해시 레이트나 레이트는 특정 압축함수에 근거한 해시함수의 효율을 엿볼 수 있다.반복 해시함수의 비율은 블록 암호 연산 수와 출력 사이의 비율을 개략적으로 나타낸다.보다 정확히 말하면, 이 비율은 $입력$ m $m$ 의 처리된 비트 수 $m$ 블록 암호의 $n$ 출력 비트 $길이$ n $n$ 및 이러한 $n$ $n$ 출력 $n$ 비트를 생성하는 데 필요한 $s$ 블록 암호 연산 $s$ ${\\displaystyle s}$ 사이의 비율을 나타낸다.일반적으로 블록 암호연산을 적게 사용하면 전체 해시함수의 전반적인 성능이 좋아지지만, 해시-값도 작아져 바람직하지 않을 수 있다.이 비율은 다음과 같은 공식으로 표현된다.

$R_{h}={\frac {\좌측 m_{i}\우측 }{s\cdot n}}$

해시함수는 적어도 다음 조건이 충족되는 경우에만 안전하다고 간주할 수 있다.

블록 암호는 동일하거나 관련된 암호화(고정 지점 또는 키 절연)를 유도하는 약한 키나 키와 같이 이상적인 암호와 구별되는 특별한 속성을 가지고 있지 않다.
결과 해시 크기는 충분히 크다.생일 공격에 따르면 보안 수준 2⁸⁰(일반적으로 현재 계산에 적합하지 않다고 가정함)^{[citation needed]}가 바람직하므로 해시 크기는 최소 160비트 이상이어야 한다.
마지막 블록은 해싱 전에 적절한 길이로 패딩되어 있다. (Merkle-Damgrdrd 시공 참조)길이 패딩은 일반적으로 SHA-1 등과 같은 전문 해시함수에서 내부적으로 구현되고 처리된다.

아래에 제시된 구조: 데이비스–마이어, 마타야스–마이어-오세아스, 미야구치-프레넬, 히로세 등은 블랙박스 분석 결과 안전한 것으로 나타났다.^[7]^[8]그 목표는 발견될 수 있는 어떤 공격도 특정한 가정 하에서 생일 공격만큼 효율적이라는 것을 보여주는 것이다.블랙박스 모델은 모든 적절한 블록 암호를 포함하는 세트에서 무작위로 선택하는 블록 암호가 사용된다고 가정한다.이 모델에서 공격자는 어떤 블록도 자유롭게 암호화하고 해독할 수 있지만, 블록 암호의 구현에 대한 접근은 할 수 없다.암호화 및 암호 해독 기능은 일반 텍스트와 키 또는 암호 텍스트와 키 쌍을 수신하는 오라클로 표현된다.그런 다음 임의로 선택한 일반 텍스트 또는 암호 텍스트로 응답한다. 만약 쌍이 처음으로 요청된 경우.두 사람 모두 쿼리와 해당 응답의 쌍인 이 세쌍둥이를 위한 테이블을 공유하고, 두 번째 쿼리가 수신되면 레코드를 반환한다.증거를 위해, 임의로 선택한 조회를 굴곡에 만드는 충돌 소견 알고리즘이 있다.알고리즘은 두 응답으로 인해 이 블록 암호 (기타 0)를 적용하는 압축함수로부터 구축된 해시함수와 관련된 충돌이 발생하는 경우 1을 반환한다.알고리즘이 1을 반환할 확률은 보안 수준을 결정하는 쿼리 수에 따라 달라진다.

데이비스-마이어

더 데이비스–Meyer 단방향 압축 함수

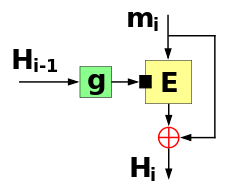
더 데이비스–Meyer 단일 블록 길이 압축 함수는 블록 암호의 키로 메시지의 각 블록( $m_{i}$ i ${\$ 을 공급한다.암호화할 일반 텍스트로 이전 해시 값( $H_{i-1}$ - $H_{i-1}$ ${\$ 을 공급한다.그런 다음 출력 암호문도 이전 해시 $H_{i-1}$ - $H_{i-1}$ 1 {\ $displaystyle H_{$ i-1 $H_{i-1}$ 을 사용하여 XORED(수치)를 하여 다음 해시 값( $H_{i}$ ${\$ 을 생성한다. $H_{i}$ 이전 해시 값이 없는 첫 번째 라운드에서는 사전 지정된 일정한 초기 값( $H_{0}$ 0 ${\$ 을 사용한다. $H_{0}$

수학 표기법 Davies–마이어는 다음과 같이 설명할 수 있다.

H_{i}=E_{m_{i}{{i-1}{(H_{i-1})}\oplus {H_{i-1}

구성표에는 다음 비율이 있다(k는 키 크기).

R_{DM}={\frac {k}{1\cdot n}={\frac {k}{n}}}}

블록 암호가 인스턴스 256비트 키를 사용하는 경우 각 메시지 블록 $m_{i}$ $m_{i}$ ${\$ 은 메시지의 256비트 청크다.동일한 블록 암호가 128비트의 블록 크기를 사용하는 경우 각 라운드의 입력 및 출력 해시 값은 128비트가 된다.

이 방법의 변형은 XOR를 32비트 부호화되지 않은 정수의 추가와 같은 다른 그룹 작업으로 대체한다.

데이비스 가문의 주목할 만한 재산–Meyer 구축은 기본 블록 암호는 완전히 안전하더라도 구성을 위한 고정점을 계산할 수 있다는 것이다. $모든$ m $m$ 에 대해 $m$ $h=E_{m}^{-1}(0)$ $E_{m}(h)\oplus h=h$ ( $E_{m}(h)\oplus h=h$ ) $E_{m}(h)\oplus h=h$ h $E_{m}(h)\oplus h=h$ = $E_{m}(h)\oplus h=h$ ${\displaystyle E_{m}\oplus h=h$ : H $h=E_{m}^{-1}(0)$ = $h=E_{m}^{-1}(0)$ m $h=E_{m}^{-1}(0)$ - $h=E_{m}^{-1}(0)$ 을 설정하기만 하면 된다 $h$ . $h=E_{m}^{-1}(0)$ $h=E_{m}^{-1}(0)$ ) $h=E_{m}^{-1}(0)$ ^[9].이것은 랜덤함수가 확실히 가지고 있지 않은 속성이다.지금까지 이 재산에 근거한 실질적인 공격은 없었으나, 이런 '특징'을 의식해야 한다.그 fixed-points 두번째 preimage 공격에(메시지를 m1{\displaystyle m_{1}} 주어진, 공격을 다른 메세지를 m2{\displaystyle m_{2}}각각 충족 해시 ⁡(m1))켈시와 슈나이어[5]의 a에 hash ⁡(m2){\displaystyle \operatorname{해시}(m_{1})=\operatorname{해시}(m_{2})}사용할 수 있 $2^{k}$ $3\times 2^{n/2+1}+2^{n-k+1}$ ${\$ $3\times 2^{n/2+1}+2^{n-k+1}$ $k$ $3\times 2^{n/2+1}+2^{n-k+1}$ -1 $2^{k}$ $3\times 2^{n/2+1}+2^{n-k+1}$ + $3\times 2^{n/2+1}+2^{n-k+1}$ + $3\times 2^{n/2+1}+2^{n-k+1}$ + 1 $3\times 2^{n/2+1}+2^{n-k+1}$ + $3\times 2^{n/2+1}+2^{n-k+1}$ + $3\times 2^{n/2+1}+2^{n-k+1}$ + 1 + 1 $3\times 2^{n/2+1}+2^{n-k+1}$ {\ $displaystyle$ 3 $^{n/2+1}+$ 2^{n-k+1}:{ $n-k$ +1}:{n-k+1}:{n-k+1}:{n1}:{n-1}:{n+ $1$ 시공으로 인해 (마타야스와 같은) 고정점을 쉽게 작성할 수 없는 경우–Meyer–Oseas 또는 Miyaguchi–Preenel) 그러면 이 공격은 $k\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ / $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 + $k\times 2^{n/2+1}+2^{n-k+1}$ + ${\$ 2 $^{n/2+1}+2^{n-k+$ 1}:{n-k+1}:{n-k+1 $}:{$ n:1}}회 $k\times 2^{n/2+1}+2^{n-k+1}$ 단위로 할 수 있다.두 경우 모두 복잡도가 $2^{n/2}$ ${\$ 스타일 $2^{n/2}}$ 보다 높지만 $2^{n/2}$ 메시지가 긴 경우 $2^{n}$ $2^{n}$ ${\$ 2 $^{n}$ 보다 낮으며, 메시지가 짧아지면 공격의 복잡성이 $2^{n}$ ${\$ 2 $^{n}}$ 에 근접한다는 점에 유의하십시오 $2^{n}$

데이비스의 보안–이상적 암호 모델에서의 마이어 구축은 R에 의해 처음 입증되었다.윈터니츠.^[10]

마타야스-마이어-오세아스

마타야스–Meyer-Oseas 단방향 압축 함수

마타야스–Meyer-Oseas 단일 블록 길이 단방향 압축 기능은 Davies의 이중(반대)으로 간주할 수 있다.-마이어.

암호화할 일반 텍스트로 메시지의 각 블록( $m_{i}$ $m_{i}$ ${\$ 을 공급한다.출력 암호문도 같은 메시지 블록( $m_{i}$ $m_{i}$ ${\$ 으로 XORED(수치)를 하여 다음 해시 값( $H_{i}$ ${\$ 을 생성한다. $H_{i}$ 이전 해시 값( $H_{i-1}$ - 1 ${\$ 을 블록 암호의 키로 공급한다.이전 해시 값이 없는 첫 번째 라운드에서는 사전 지정된 일정한 초기 값( $H_{0}$ 0 ${\$ 을 사용한다. $H_{0}$

블록 암호의 블록과 키 크기가 다른 경우, 해시 값( $H_{i-1}$ - $H_{i-1}$ ${\$ 은 키로 사용하기 위한 크기가 잘못된다.암호는 키에 대한 다른 특별한 요구사항도 가지고 있을 수 있다.그런 다음 해시 값은 먼저 함수 $g$ $g$ 를 통해 공급되어 $g$ 암호의 키로 적합하도록 변환/패딩된다.

수학 표기법에서 마트야스–Meyer-Oseas는 다음과 같이 설명할 수 있다.

H_{i}=E_{g(H_{i-1})}(m_{i})\oplus m_{i}}

이 계획에는 다음과 같은 비율이 있다.

R_{MMO}={\frac {n}{1\cdot n}=1

두번째 preimage 공격(메시지를 m1{\displaystyle m_{1}}를 주어진 공격자를 찾는다 다른 메세지를 m2{\displaystyle m_{2}}각각 충족 해시 ⁡(m1))hash ⁡(m2){\displaystyle \operatorname{해시}(m_{1})=\operatorname{해시}(m_{2})})이 될 수 있는 일에 따르면 켈시와 Schneier[5]에 대한 2k. ${\displaystyle 2^{k}}-$ block $2^{k}$ $k\times 2^{n/2+1}+2^{n-k+1}$ in $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ / $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 + $k\times 2^{n/2+1}+2^{n-k+1}$ - $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 ${\$ 2^{ $n/2+1}+2^{n-k+$ 1}:{n-k+1}:{n-k $+$ 1}:{n2 $k\times 2^{n/2+1}+2^{n-k+1}$ 복잡도는 $2^{n/2}$ / $2^{n/2}$ ${\$ 보다 높지만 $2^{n/2}$ 메시지가 긴 경우 $2^{n}$ $2^{n}$ ${\$ 2 $^{n}}$ 보다 낮으며, 메시지가 짧아지면 공격의 복잡성이 $2^{n}$ ${\$ 에 근접한다는 점에 유의하십시오 $2^{n}$

미야구치프레넬

미야구치-프레넬 단방향 압축 기능

미야구치-프레넬 단일 블록 길이 단방향 압축함수는 마타야스의 확장 변형이다.–마이어-오세아스.미야구치 쇼지와 바트 프레넬이 독자적으로 제안한 것이다.

암호화할 일반 텍스트로 메시지의 각 블록( $m_{i}$ $m_{i}$ ${\$ 을 공급한다.그런 다음 출력 암호문을 동일한 메시지 블록( $m_{i}$ i ${\$ 으로 XORED(수직)한 다음, 이전 해시 값( $H_{i-1}$ - $H_{i-1}$ {\ $displaystyle H_{i-1$ 으로 XORED하여 다음 해시 값( $H_{i}$ {\ $displaystystyle H_{i}}})$ 을 생성한다.이전 해시 값( $H_{i-1}$ - 1 ${\$ 을 블록 암호의 키로 공급한다.이전 해시 값이 없는 첫 번째 라운드에서는 사전 지정된 일정한 초기 값( $H_{0}$ 0 ${\$ 을 사용한다. $H_{0}$

블록 암호의 블록과 키 크기가 다른 경우, 해시 값( $H_{i-1}$ - $H_{i-1}$ ${\$ 은 키로 사용하기 위한 크기가 잘못된다.암호는 키에 대한 다른 특별한 요구사항도 가지고 있을 수 있다.그런 다음 해시 값은 먼저 함수 $g$ $g$ 를 통해 공급되어 $g$ 암호의 키로 적합하도록 변환/패딩된다.

수학적 표기법에서 미야구치-프레넬은 다음과 같이 설명할 수 있다.

H_{i}=E_{g(H_{i-1})}(m_{i})\oplus H_{i-1}\oplus m_{i}}

이 계획에는 다음과 같은 비율이 있다.

R_{MP}={\frac {n}{1\cdot n}=1

$H_{i-1}$ $m_{i}$ ${\$ 과 $m_{i}$ (와) $H_{i-1}$ - $H_{i-1}$ ${\$ 의 역할을 전환할 수 있으므로 $H_{i-1}$ , $H_{i-1}$ - 1 $H_{i-1}$ {\ $displaystyle H_{i-1}$ 키 $m_{i}$ $m_{i}$ ${\$ 에 암호화되어 이 방법은 $H_{i-1}$ 데이비스의 확장이다.-대신 마이어.

두번째 preimage 공격(메시지를 m1{\displaystyle m_{1}}를 주어진 공격자를 찾는다 다른 메세지를 m2{\displaystyle m_{2}}각각 충족 해시 ⁡(m1))hash ⁡(m2){\displaystyle \operatorname{해시}(m_{1})=\operatorname{해시}(m_{2})})이 될 수 있는 일에 따르면 켈시와 Schneier[5]에 대한 2k. ${\displaystyle 2^{k}}-$ block $2^{k}$ $k\times 2^{n/2+1}+2^{n-k+1}$ in $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ / $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 + $k\times 2^{n/2+1}+2^{n-k+1}$ - $k\times 2^{n/2+1}+2^{n-k+1}$ k $k\times 2^{n/2+1}+2^{n-k+1}$ + 1 ${\$ 2^{ $n/2+1}+2^{n-k+$ 1}:{n-k+1}:{n-k $+$ 1}:{n2 $k\times 2^{n/2+1}+2^{n-k+1}$ 복잡도는 $2^{n/2}$ / $2^{n/2}$ ${\$ 보다 높지만 $2^{n/2}$ 메시지가 긴 경우 $2^{n}$ $2^{n}$ ${\$ 2 $^{n}}$ 보다 낮으며, 메시지가 짧아지면 공격의 복잡성이 $2^{n}$ ${\$ 에 근접한다는 점에 유의하십시오 $2^{n}$

히로세

Hirose 이중 블록 길이 압축 기능

히로세^[8] 더블 블록 길이 단방향 압축 함수는 블록 암호에 순열 $[\displaystyle p}$ 를 더한 것으로 $p$ 2006년 히로세 쇼이치로부터 제안받았으며, Mridul Nandi의 작품을^[11] 원작으로 하고 있다.

키 길이 $k$ $k$ 이 $k$ (가) 블록 $길이$ n ${\displaystyle n$ 보다 큰 블록 암호를 사용하며, 크기 $2n$ $2n$ 의 해시를 생성한다 $2n$ 예를 들어 192비트 또는 256비트 키(및 128비트 블록)를 가진 AES 후보 중 누구라도 해당된다.

각 라운드는 k - $m_{i}$ ${\$ k-n $}$ 비트 길이의 $k-n$ $k-n$ $m_{i}$ i {\ $displaystyle m_$ ${i}$ 일부를 수신하고 이를 사용하여 두 $n$ 의 n $n$ -bit $n$ 상태 값 $G$ $G$ 및 $H$ ${\\displaystystyle H}$ 을 업데이트한다 $H$

먼저 $m_{i}$ $m_{i}$ $m_{i}$ ${\$ 을 $H_{i-1}$ - 1 ${\$ 와 $H_{i-1}$ 연결하여 키 $K_{i}$ ${\$ 를 생성한다 $K_{i}$ 그런 다음 두 피드백 값은 다음에 따라 업데이트된다.

$G_{i}=E_{K_{i}}(G_{i-1})\oplus G_{i-1$
$H_{i}=E_{K_{i-}(p_{i-1})\oplus p(G_{i-1})$

$p(G_{i-1})$ ( $p(G_{i-1})$ - 1 $p(G_{i-1})$ ) ${\displaystyle p(G_{i-1})$ 는 $n$ $n$ -bit $n$ 값에 대한 임의 고정점 없는 순열이며 $p(G_{i-1})$ , 임의의 0이 아닌 $상수$ c ${\\displaystyle c}$ 에 대해 $p(x)=x\oplus c$ $p(x)=x\oplus c$ 으로 p $p(x)=x\oplus c$ ( $x$ = $x$ c ${\displaysty$ c $}$ 로 정의된다. $c$

각 암호화는 표준 Davies와 유사함–마이어 구조.제안된 다른 이중 블록 길이 체계보다 이 체계의 장점은 두 암호화 모두 동일한 키를 사용하므로 키 스케줄링 노력이 공유될 수 있다는 것이다.

최종 출력은 $H_{t}||G_{t}$ $H_{t}||G_{t}$ $H_{t}||G_{t}$ $H_{t}||G_{t}$ ${\$ 입니다 $H_{t}||G_{t}$ 체계에는 암호로 메시지를 암호화하는 것과 관련된 ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ = k ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ - ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$ ${\$ { $k-n}{2n}}}$ 의 비율이 있다.

히로세는 또한 이상 암호 모델에서 증거를 제공한다.

스펀지 시공

스펀지 구조는 단방향 압축 기능을 구축하는 데 사용될 수 있다.

참고 항목

월풀 — 미야구치-프레넬 구조를 사용하여 구축된 암호 해시 함수로서, 스퀘어 및 AES와 유사한 블록 암호다.
CBC-MAC, OMAC 및 PMAC — 블록 암호를 MAC(메시지 인증 코드)로 변환하는 방법.

참조

인용구

^ Alfred J. Menez, Paul C. van Ourschot, Scott A의 응용 암호 안내서.밴스톤.5번째 인쇄(2001년 8월) 페이지 328.
^ "Announcing the first SHA1 collision". Google Online Security Blog. Retrieved 2020-01-12.
^ 이반 담그드해시 함수에 대한 설계 원리.길레스 브라사드, CRYPLO 편집자, LNCS 435권, 416-427페이지.1989년 스프링거
^ 랄프 머클단방향 해시함수와 DES.길레스 브라사드, CRYPLO 편집자, LNCS 435권, 428-446페이지.1989년 스프링거
^ ^a ^b ^c ^d 존 켈시와 브루스 슈나이어.n비트 해시함수에 대한 두 번째 사전 설정 작업 2개ⁿ 미만.로널드 크레이머, EUROCYPT 편집자, LNCS 3494쪽 474-490쪽2005년 스프링거
^ 존 블랙, 마틴 코크란, 토마스 슈림튼.고효율 블록시퍼 기반 해시함수의 불가능성에 대하여.암호학의 발전 – EUROCHYPT '05, 덴마크 아르후스, 2005.저자들은 해시함수를 정의한다. "해시함수의 압축함수가 키가 고정된 블록 암호에 정확히 한 번의 호출을 사용하는 경우, 매우 효율적"
^ 존 블랙, 필립 로가웨이, 톰 슈림튼.PGV에서 블록-시퍼 기반 해시함수 구조물의 블랙박스 해석암호학의 진보 – CRIPTO '02, 컴퓨터 과학의 강의 노트, vol. 2442, 페이지 320–335, Springer, 2002.3페이지의 Davies 표 참조–마이어, 마타야스–마이어-오세아스와 미야구치-프레넬은 첫 번째 열에 해시함수 5, 1, 3으로 번호가 매겨진다.
^ ^a ^b S. 히로세, 이중 블록-길이 해시함수의 일부 그럴듯한 구성.인: Robshaw, M. J. B. (ed.) FSE 2006, LNCS, 4047, 페이지 210–225, 스프링거, 하이델베르크 2006.
^ Alfred J. Menez, Paul C. van Ourschot, Scott A의 응용 암호 안내서.밴스톤.5번째 인쇄(2001년 8월) 페이지 375.
^ 윈터니츠 R. 윈터니츠DES에서 작성된 보안 단방향 해시 함수.IEEE 정보보안 및 프라이버시에 관한 심포지엄의 절차서, 페이지 88-90.IEEE 프레스, 1984.
^ M. 난디, 최적의 이중 길이 해시함수를 지향하여 In: In: India에서 제6차 국제 암호학 회의(INDOCRYPT 2005), 컴퓨터 과학의 강의 노트 3797, 77–89, 2005.

원천

Menezes; van Oorschot; Vanstone (2001). "Hash Functions and Data Integrity" (PDF). Handbook of Applied Cryptography.

[1] Alfred J. Menez, Paul C. van Ourschot, Scott A의 응용 암호 안내서.밴스톤.5번째 인쇄(2001년 8월) 페이지 328.

[2] "Announcing the first SHA1 collision". Google Online Security Blog. Retrieved 2020-01-12.

[damgard89-3] 이반 담그드해시 함수에 대한 설계 원리.길레스 브라사드, CRYPLO 편집자, LNCS 435권, 416-427페이지.1989년 스프링거

[merkle89-4] 랄프 머클단방향 해시함수와 DES.길레스 브라사드, CRYPLO 편집자, LNCS 435권, 428-446페이지.1989년 스프링거

[ks05-5] 존 켈시와 브루스 슈나이어.n비트 해시함수에 대한 두 번째 사전 설정 작업 2개ⁿ 미만.로널드 크레이머, EUROCYPT 편집자, LNCS 3494쪽 474-490쪽2005년 스프링거

[6] 존 블랙, 마틴 코크란, 토마스 슈림튼.고효율 블록시퍼 기반 해시함수의 불가능성에 대하여.암호학의 발전 – EUROCHYPT '05, 덴마크 아르후스, 2005.저자들은 해시함수를 정의한다. "해시함수의 압축함수가 키가 고정된 블록 암호에 정확히 한 번의 호출을 사용하는 경우, 매우 효율적"

[7] 존 블랙, 필립 로가웨이, 톰 슈림튼.PGV에서 블록-시퍼 기반 해시함수 구조물의 블랙박스 해석암호학의 진보 – CRIPTO '02, 컴퓨터 과학의 강의 노트, vol. 2442, 페이지 320–335, Springer, 2002.3페이지의 Davies 표 참조–마이어, 마타야스–마이어-오세아스와 미야구치-프레넬은 첫 번째 열에 해시함수 5, 1, 3으로 번호가 매겨진다.

[Hirose06-8] S. 히로세, 이중 블록-길이 해시함수의 일부 그럴듯한 구성.인: Robshaw, M. J. B. (ed.) FSE 2006, LNCS, 4047, 페이지 210–225, 스프링거, 하이델베르크 2006.

[9] Alfred J. Menez, Paul C. van Ourschot, Scott A의 응용 암호 안내서.밴스톤.5번째 인쇄(2001년 8월) 페이지 375.

[10] 윈터니츠 R. 윈터니츠DES에서 작성된 보안 단방향 해시 함수.IEEE 정보보안 및 프라이버시에 관한 심포지엄의 절차서, 페이지 88-90.IEEE 프레스, 1984.

[11] M. 난디, 최적의 이중 길이 해시함수를 지향하여 In: In: India에서 제6차 국제 암호학 회의(INDOCRYPT 2005), 컴퓨터 과학의 강의 노트 3797, 77–89, 2005.

[1]

[2]

[3]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

Search