폴링의 법칙

폴링의 법칙은 1929년 라이너스 폴링이 이온 화합물의 결정 구조를 예측하고 합리화하기 위해 발표한 5가지 규칙입니다.^[1]^[2]

첫 번째 규칙: 반지름 비율 규칙

전형적인 이온 고체의 경우, 양이온은 음이온보다 작고, 각각의 양이온은 다면체를 형성하는 배위 음이온으로 둘러싸여 있습니다. 이온 반경의 합은 양이온-음이온 거리를 결정하고, 양이온-음이온 반지름 $r_{+}/r_{-}$ + $r_{+}/r_{-}$ / $r_{+}/r_{-}$ - $r_{+}/r_{-}$ {\ $display r_{+}/r_{-}($ $r_{c}/r_{a}$ $r_{c}/r_{a}$ c $r_{c}/r_{a}$ / $r_{c}/r_{a}$ {\ $display r_{c}/r_{a$ 은 양이온의 배위수(C.N.)와 음이온의 배위 다면체의 모양을 결정합니다.^[2]^{: 524}^[3]

아래 표의 배위 번호와 대응하는 다면체의 경우, 폴링은 양이온이 주어진 음이온 수(이온을 강체구로 간주)와 접촉하는 최소 반지름 비율을 수학적으로 도출했습니다. 양이온이 더 작으면 음이온과 접촉하지 않아 불안정성이 발생하여 배위수가 낮아집니다.

*임계 반지름 비율*. 이 다이어그램은 좌표 번호 6: 표시된 평면에 음이온 4개, 평면 위에 1개, 아래에 1개가 있습니다. 안정성 한계는 r/r = 0.414입니다.

각 배위수에 대한 다면체 및 최소 반지름 비율
C.N.	다면체	반지름비
3	삼각형의	0.155
4	사면체의	0.225
6	팔면체의	0.414
7	뚜껑이 달린 팔면체	0.592
8	사각 안티프리즘(안티큐브)	0.645
8	정육면체	0.732
9	3배증삼각기둥	0.732
12	정육면체	1.00

오른쪽에 있는 세 개의 다이어그램은 좌표 번호가 6개인 팔면체 좌표에 해당합니다. 즉, 다이어그램의 평면에 4개의 음이온이 있고, 이 평면 위와 아래에 2개(미도시)가 있습니다. 중앙 다이어그램에는 최소 반경 비율이 표시됩니다. 양이온과 임의의 두 음이온은 2 $2r_{-}={\sqrt {2}}(r_{-}+r_{+})$ - = $2r_{-}={\sqrt {2}}(r_{-}+r_{+})$ (r $-$ + ${\sqrt {2}}r_{-}=r_{-}+r_{+}$ + ) ${\displaystyle$ 2r_{-}={\ $sqrt {$ 2}}( $r_{-}+r_$ {+})} 또는 2 r - = r - + r + {\displaystyle {\sqrt {2}}r_{-}= r_{-}+r_{+}}인 직각 삼각형을 형성합니다. 그런 다음 $r_{+}=({\sqrt {2}}-1)r_{-}=0.414r_{-}$ + = $r_{+}=({\sqrt {2}}-1)r_{-}=0.414r_{-}$ ( $r_{+}=({\sqrt {2}}-1)r_{-}=0.414r_{-}$ - $r_{+}=({\sqrt {2}}-1)r_{-}=0.414r_{-}$ ) r - = 0.414 r - {\displaystyle r_{+} = ({\sqrt {2}-1)r_{-} = 0.414r_{-}-}입니다. 유사한 기하학적 증명은 대칭성이 높은 경우 CN = 3, 4, 8에 대한 최소 반지름 비율을 산출합니다.

CN = 6이고 최소보다 큰 반지름 비율의 경우 양이온이 6개의 음이온과 여전히 접촉하고 있기 때문에 결정이 더 안정적이지만 음이온이 서로 더 멀리 떨어져 있으므로 상호 반발력이 줄어듭니다. 그러면 반지름 비율이 0.414 이상인 팔면체가 형성될 수 있지만 비율이 0.732 이상으로 증가할수록 입방 기하학이 안정됩니다. 이것이 이유를 설명해 줍니다. 반경비가 0.55인 NaCl의 Na는⁺ 8면체 배위를 갖는 반면, 반경비가 0.93인 CsCl의 Cs는⁺ 입방배위를 갖는 것입니다.^[5]

반지름 비율이 최소값보다 작으면 2개의 음이온이 이탈하고 나머지 4개는 양이온과 접촉하는 사면체 기하학으로 재배열되는 경향이 있습니다.

반지름 비율 규칙은 좌표 수를 예측하는 데 어느 정도 성공한 첫 번째 근사치이지만 많은 예외가 존재합니다.^[3] 5,000개 이상의 산화물 집합에서 배위 환경의 66%만이 폴링의 첫 번째 규칙에 동의합니다. 복수의 양이온 배위를 포함하는 알칼리 또는 알칼리 토금속 양이온으로 형성된 산화물은 이 규칙으로부터 일반적인 편차입니다.^[6]

두 번째 규칙: 정전 원자가 규칙

주어진 양이온에 대해 폴링은 각 배위 음이온에 대한 정전기적 결합 강도를 $s={\frac {z}{\nu }}$ = $s={\frac {z}{\nu }}$ ν $s={\frac {z}{\nu }}$ {\displaystyle s = {\ $frac$ {z}{\n으로 정의했습니다. $u$ 여기서 z는 양이온 전하, $ν$ 는 양이온 배위 번호입니다. 안정적인 이온 구조는 국부적인 전자 중성을 보존하도록 배치되어 음이온에 대한 정전기 결합의 세기의 합이 해당 음이온의 전하와 동일합니다.

\xi =\sum _{i}s_{i}

여기서 $\xi$ ξ ${\displaystyle$ \xi $}$ 는 음이온 전하이고 합산은 인접 양이온 위에 있습니다. 단순 고체의 경우 $s_{i}$ ${\$ 는 주어진 음이온에 배위된 모든 양이온에 대해 동일하므로 $s_{i}$ 음이온 배위 수는 음이온 전하를 각 정전기 결합 강도로 나눈 값입니다. 몇 가지 예가 표에 나와 있습니다.

산화물²⁻ 이온이 있는 양이온

양이온	반지름비	양이온 C.N.	정전기적 결속력	음이온 씨엔.
리⁺	0.34	4	0.25	8
Mg²⁺	0.47	6	0.33	6
스크³⁺	0.60	6	0.5	4

폴링은 이 규칙이 세 가지 다른 양이온을 가진 알루미노실리케이트 광물 오르토클라제인 KAlSiO와₃₈ 같은 더 복잡한 결정을 고려할 수 있는 가능한 구조를 제한하는 데 유용하다는 것을 보여주었습니다.^[2] 그러나 ICSD(Imonal Crystal Structure Database)의 산화물에 대한 데이터 분석 결과, 모든 산소 원자의 20%만이 두 번째 규칙(0.01 컷오프 사용)의 예측과 일치하는 것으로 나타났습니다.^[6]

세 번째 규칙: 다면체 모서리, 모서리 및 면의 공유

두 개의 음이온 다면체에 의한 가장자리와 특히 면의 공유는 이온 구조의 안정성을 감소시킵니다. 모서리를 공유해도 안정성이 크게 저하되지 않으므로 (예를 들어) 팔면체가 서로 모서리를 공유할 수 있습니다.^[2]^{: 559}

안정성이 떨어지는 것은 가장자리와 면을 공유하면 양이온이 서로 더 가까이 배치되어 양이온-양이온 정전기적 반발력이 증가하기 때문입니다. 높은 전하와 낮은 CN을 갖는 양이온(특히 r+/r-가 다면체 안정성의 하한에 접근할 때)의 효과가 가장 큽니다. 일반적으로 작은 요소가 규칙을 더 잘 수행합니다.^[6]

한 예로, Pauling은 이산화티타늄의 세 가지 광물 형태를 고려했는데, 각각은⁴⁺ Ti의 배위 번호가 6입니다. 가장 안정적인(그리고 가장 풍부한) 형태는 루타일(rutile)인데, 이 루타일은 배위 팔면체가 각각 인접한 팔면체와 두 개의 모서리(얼굴은 없음)만을 공유하도록 배열되어 있습니다. 덜 안정적인 다른 두 가지 형태는 브루카이트와 아나타제이며, 각 팔면체는 인접한 팔면체와 각각 3개와 4개의 가장자리를 공유합니다.^[2]^{: 559}

네 번째 규칙: 서로 다른 양이온을 포함하는 결정

서로 다른 양이온을 포함하는 결정에서 원자가가 높고 배위 수가 작은 결정은 다면체 요소를 서로 공유하지 않는 경향이 있습니다.^[2]^{: 561} 이 규칙은 대전된 양이온 사이의 거리를 증가시켜 양이온 사이의 정전기적 반발력을 줄이는 경향이 있습니다.

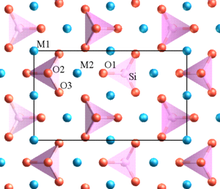
폴링의 예 중 하나는 감람석, MSiO인데₂₄, 여기서 M은 일부 부위의 Mg와²⁺ 다른²⁺ 부위의 Fe의 혼합물입니다. 이 구조에는 서로 산소를 공유하지 않는 뚜렷한 SiO₄ 4면체가 포함되어 있습니다(코너, 모서리 또는 면). 저가 Mg과²⁺ Fe는²⁺ 산소를 공유하는 다면체로 둘러싸여 있습니다.

다섯 번째 규칙: 간결성의 규칙

결정 안에 본질적으로 다른 종류의 성분의 수가 적은 경향이 있습니다.^[2] 구조의 각 원자가 특정 환경에서 가장 안정적이기 때문에 반복 단위는 동일한 경향이 있습니다. 다면체는 사면체나 팔면체와 같이 2~3가지 종류가 있을 수 있지만 종류가 많지는 않을 것입니다.

리미트먼트

5000개의 산화물을 대상으로 한 연구에서 13%만이 마지막 4가지 규칙을 모두 만족하고 있으며, 이는 폴링 규칙의 제한된 보편성을 나타냅니다.^[6]

참고 항목

참고문헌

^ Pauling, Linus (1929). "The principles determining the structure of complex ionic crystals". J. Am. Chem. Soc. 51 (4): 1010–1026. doi:10.1021/ja01379a006.
^ ^a ^b ^c ^d ^e ^f ^g ^h Pauling, Linus (1960). The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry (3rd ed.). Ithaca (NY): Cornell University Press. pp. 543–562. ISBN 0-8014-0333-2.
^ ^a ^b Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic chemistry (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. p. 145. ISBN 9780130399137.
^ Toofan, Jahansooz (February 1994). "A Simple Expression between Critical Radius Ratio and Coordination Number". Journal of Chemical Education. 71 (2): 147. doi:10.1021/ed071p147. Following the erratum, equations should read $\alpha =\arcsin {({\tfrac {12-CN}{12}})^{\tfrac {1}{2}}}$ and $R=({\tfrac {12}{12-CN}})^{\tfrac {1}{2}}{-1}$ , (여기서 $2\alpha =$ = ${\$ displaystyle 2\alpha =} 결합 각도)
^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General chemistry: principles and modern applications (8th ed.). Upper Saddle River, NJ: Prentice Hall. p. 518. ISBN 0-13-014329-4.
^ ^a ^b ^c ^d George, Janine; Waroquiers, David; Di Stefano, Davide; Petretto, Guido; Rignanese, Gian‐Marco; Hautier, Geoffroy (2020-05-04). "The Limited Predictive Power of the Pauling Rules". Angewandte Chemie International Edition. 59 (19): 7569–7575. doi:10.1002/anie.202000829. ISSN 1433-7851. PMC 7217010. PMID 32065708.

[1] Pauling, Linus (1929). "The principles determining the structure of complex ionic crystals". J. Am. Chem. Soc. 51 (4): 1010–1026. doi:10.1021/ja01379a006.

[Pauling1960-2] ^ ^a ^b ^c ^d ^e ^f ^g ^h Pauling, Linus (1960). The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry (3rd ed.). Ithaca (NY): Cornell University Press. pp. 543–562. ISBN 0-8014-0333-2.

[Housecroft-3] Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic chemistry (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. p. 145. ISBN 9780130399137.

[4] Toofan, Jahansooz (February 1994). "A Simple Expression between Critical Radius Ratio and Coordination Number". Journal of Chemical Education. 71 (2): 147. doi:10.1021/ed071p147. Following the erratum, equations should read $\alpha =\arcsin {({\tfrac {12-CN}{12}})^{\tfrac {1}{2}}}$ and $R=({\tfrac {12}{12-CN}})^{\tfrac {1}{2}}{-1}$ , (여기서 $2\alpha =$ = ${\$ displaystyle 2\alpha =} 결합 각도)

[5] Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General chemistry: principles and modern applications (8th ed.). Upper Saddle River, NJ: Prentice Hall. p. 518. ISBN 0-13-014329-4.

[:0-6] George, Janine; Waroquiers, David; Di Stefano, Davide; Petretto, Guido; Rignanese, Gian‐Marco; Hautier, Geoffroy (2020-05-04). "The Limited Predictive Power of the Pauling Rules". Angewandte Chemie International Edition. 59 (19): 7569–7575. doi:10.1002/anie.202000829. ISSN 1433-7851. PMC 7217010. PMID 32065708.

[1]

[2]

[3]

[5]

[6]

v t 리누스 폴링
출판물	화학결합의 본질 (1939년 저서) 낫 세포 빈혈, 분자 질환 (1949년 논문) 비타민C와 감기 (1970년 책) 더 오래 살고 더 기분 좋게 사는 법 (1986)
컨셉트	원자가결합이론 궤도 교잡 공명 폴링 전기음성도 척도 폴링의 법칙
설립	라이너스 폴링 연구소 국제휴머니스트연맹
관련된	아바 헬렌 폴링(아내) 분자의학 비타민C 메가도세이지 아스코르브산 정맥주사 리누스 폴링상 폴링 필드 4674 Pauling

Search