육팔면체

정육면체 그래프
정육면체 그래프
	4배 대칭
꼭지점	12
가장자리	24
자기동형	48
특성.	4진법; 해밀턴식; 규칙적인.; 국소적으로 선형의;
	그래프 및 매개 변수 표

육팔면체
(회전 모델을 보려면 여기를 클릭)
유형	아르키메데스의 입체 균일한 다면체
요소들	F = 14, E = 24, V = 12 (표준 = 2)
측면 나란히	8{3}+6{4}
콘웨이 표기법	AC AAT
슐레플리 기호	r{4,3} 또는 ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ { ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ .3 $}{$ rr { 3,3} $r{\begin{Bmatrix}3\\3\end{Bmatrix}}$ { $r{\begin{Bmatrix}3\\3\end{Bmatrix}}$ $}$ { $displaystyle$ r { \ $begin$ { $Bmatrix }$ 3 \ \ $3$ \ $end$ { $Bmatrix$ } }
슐레플리 기호	t₁{4,3} 또는_0,2 t{3,3}
위토프 기호	2 3 4 3 3 2
콕서터 다이어그램	또는 또는
대칭군	O_h, B₃, [4,3], (432), 주문 48 T_d, [3,3], (332), 순서 24
로테이션 그룹	O, [4,3],⁺ (432), 주문 24
이면각	125.26° arcsec(호 3)
레퍼런스	U₀₇, C₁₉, W₁₁
특성.	반규칙 볼록 준규격
유색인종	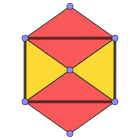3.4.3.4 (버텍스 그림)
마름모꼴 12면체 (입체 다면체)	그물

정육면체의 3D 모형

정육면체는 8개의 삼각형 면과 6개의 정사각형 면을 가진 다면체이다.정육면체는 각각 두 개의 삼각형과 두 개의 정사각형이 만나는 12개의 동일한 정점과 각각 세모꼴과 정사각형을 구분하는 24개의 동일한 모서리가 있습니다.이와 같이, 그것은 준정규 다면체, 즉 정점-추이적일 뿐만 아니라 모서리-추이적인 ^[1]아르키메데스의 고체이다.그것은 반지름으로 등각이다.

그것의 이중 다면체는 마름모꼴 12면체이다.

플라톤은 아마도 육팔면체를 알고 있었을 것이다.헤론의 정의에서는 플라톤이 8개의 삼각형과 ^[2]6개의 정사각형으로 이루어진 고체를 알고 있었다고 아르키메데스를 인용한다.

동의어

벡터 평형(Buckminster Fuller)은 중심에서 수직까지의 반지름이 모서리 길이와 같기 때문입니다(반경적 등변 대칭을 가집니다).Fuller는 또한 단단한 스트럿과 유연한 정점으로 만들어진 정육면체를 지터버그라고 불렀습니다; 이 물체는 정사각형의 ^[3]대각선을 따라 접힘으로써 점진적으로 20면체, 8면체, 그리고 4면체로 변할 수 있습니다.
O 대칭, 차수 48의 경우_h, 정류된 정육면체 또는 정류된 8면체입니다(노먼 존슨).
T 대칭, 24차, 이것은 구분이_d 되는 사면체 또는 마름비테트라면체이다.
D 대칭, 12차, 이것은_3d 삼각형 자이로비쿠폴라입니다.

직교 투영

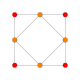
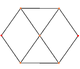
정육면체에는 꼭지점, 모서리, 그리고 삼각형과 정사각형이라는 두 가지 유형의 면을 중심으로 네 개의 특별한 직교 투영부가 있습니다.마지막 두 개는 B와₂₂ A 콕서터 평면에 해당합니다.스큐 투영법은 정사각형과 육각형이 정육면체의 중심을 통과하는 것을 보여줍니다.

정육면체(직교 투영)
광장 얼굴	삼각형의 얼굴	꼭지점	엣지


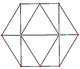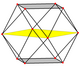[4]	[6]	[2]	[2]
마름모꼴 12면체(이중 다면체)

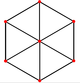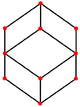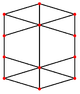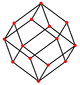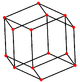구면 타일링

육면체는 구면 타일링으로 표현될 수 있으며 입체 투영을 통해 평면에 투영될 수 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면의 직선은 평면에 원형 호로 투영됩니다.

맞춤법 투영법	정사각형 중심의	삼각형의	정점 중심

맞춤법 투영법	입체 투영

구조.

좌표

원점을^[4] 중심으로 한 정육면체의 정점에 대한 데카르트 좌표는 다음과 같다.

(±1,±1,0)

(±1,0,±1)

(0,±1,±1)

대체 좌표 집합은 다음과 같은 12개의 순열로 4개의 공간으로 만들 수 있습니다.

(0,1,1,2)

이 구조는 칸텔화 16셀의 16개의 직교면 중 하나로 존재합니다.

루트 벡터

정육면체의 12개의 꼭지점은 단순한 Lie 그룹₃ A의 루트 벡터를 나타낼 수 있습니다.팔면체의 정점 6개를 더하면, 이 정점들은 단순한 Lie 그룹₃ B의 18개의 루트 벡터를 나타냅니다.

메트릭 속성

면적 A와 모서리 길이 a의 정육면체의 부피 V는 다음과 같다.

디스플레이 스타일A&=\left(6+2{\sqrt {3}}\right)a^{2}&\약 9.464,1016a^{2}\\\\V&=tfrac {5}{\twrt {2}}a^{3}&\약 2.357,0226a^{3}.\end { aligned}}

절개요

정팔면체와 정팔면체

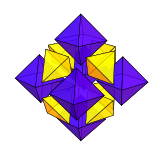
정육면체는 중앙점에서 만나는 6개의 정사각형 피라미드와 8개의 사면체로 해부될 수 있습니다.이 해부는 정사각형 피라미드 쌍이 팔면체로 결합되는 사면체-팔면체 벌집 형태로 표현됩니다.

불규칙 다면체

정육면체는 정육면체의 ^[a]중심을 통과하는 공통의 육각형에 의해 두 개의 삼각형 큐폴라로 해부될 수 있다.이 두 개의 삼각 큐폴라가 삼각형과 정사각형이 일렬로 정렬되도록 꼬이면 Johnson 솔리드₂₇ J(삼각형 직소성 우폴라)가 생성됩니다.

기하 관계

정팔면체로 확장되어 정팔면체로 확장되고, 정팔면체로 역팽창되는 정팔면체 사이의 진행

반지름 등변 대칭

정육면체에서 긴 반지름(중앙에서 정점)은 모서리 길이와 같기 때문에 긴 지름(대각에서 반대 정점까지)은 두 모서리 길이입니다.그것의 중심은 피라미드의 정점과 같다: 다른 모든 정점에서 한 모서리 길이만큼 떨어져 있다.(입방팔면체의 경우, 중심은 사실 6개의 정사각형과 8개의 삼각형 피라미드의 정점입니다.)이 반지름 등변 대칭은 2차원 육각형, 3차원 육면체, 4차원 24셀과 8셀(테서랙트)을 포함한 몇 개의 균일한 폴리톱의 특성이다.반지름 등변 폴리톱은 각각 2개의 반지름과 가장자리를 이루는 등변 삼각형에서 긴 반지름으로 구성될 수 있는 폴리톱이다.따라서, 이러한 다면체의 중심에서 만나는 모든 내부 요소들은 6개의 정사각형 피라미드와 8개의 사면체로 된 정사면체의 분해에서와 같이 정삼각형 내면을 가지고 있다.

이들 반경방향 등변 폴리톱은 각각 정육면체의 타일링, 정류입방체벌집(교대입방정체 및 옥타헤드라), 24셀벌집, 정사벌집 등 공간충전 테셀레이션의 세포로서도 발생한다.각 테셀레이션에는 이중 테셀레이션이 있습니다. 테셀레이션의 셀 중심은 이중 테셀레이션의 셀 꼭지점입니다.2차원, 3차원 및 4차원으로 알려진 가장 밀도가 높은 규칙적인 구체 패킹은 이러한 테셀레이션 중 하나의 셀 중심을 구 중심으로 사용합니다.

정육면체는 팔면체 대칭을 가지고 있다.그것의 첫 번째 단계화는 입방체와 그것의 이중 팔면체의 화합물이며, 입방체의 꼭지점은 둘 중 하나의 모서리의 중간점에 위치한다.

구성

4차원 24셀 또는 16셀의 적도 단면을 취함으로써 정육면체를 얻을 수 있다.정육면체의 적도 단면을 취함으로써 육각형 또는 정사각형을 얻을 수 있다.

정육면체는 정류된 입방체이며 정류된 팔면체이기도 하다.

그것은 또한 캔텔레이트된 사면체이다.이 구조에서는 와이토프 기호가 지정됩니다: 3 3 2.

사면체의 스큐 칸테레이션은 정육면체의 면과 평행한 면, 즉 두 크기의 삼각형 8개와 직사각형 6개를 가진 고체를 생성한다.가장자리가 동일하지 않은 반면, 이 고체는 정점이 균일하게 유지됩니다. 즉, 고체는 완전한 사면체 대칭 그룹을 가지며 그 그룹 아래에서 정점은 동일합니다.

정육면체의 모서리는 네 개의 정육각형을 이룬다.육면체를 육각형 중 하나의 평면에서 자르면, 각각의 절반은 존슨 고체 중 하나인 삼각 큐폴라이다. 따라서 육면체 자체는 시리즈 중 가장 단순한 삼각형 자이로비큐폴라라고도 할 수 있다(자이로비파스티기움 또는 "이색 자이로비큐폴라"를 제외하고).삼각형이 삼각형과 정사각형과 정사각형이 정사각형과 만나도록 반반전을 다시 합치면, 그 결과는 반팔면체라고도 불리는 또 다른 Johnson 솔리드, 즉 삼각 정소수성 우폴라가 됩니다.

두 삼각형 쌍두포라는 구면 패킹에서 중요하다.솔리드의 중심에서 정점까지의 거리는 솔리드의 가장자리 길이와 동일합니다.각 중심구는 최대 12개의 이웃을 가질 수 있으며, 면 중심의 입방체 격자에서 이것들은 정육면체의 정점의 위치를 차지합니다.육각형 밀착 격자에서 이들은 삼각형 직소성 우폴라의 모서리에 해당합니다.두 경우 모두 중심 구는 솔리드의 중심 위치를 차지합니다.

큐빅타헤드라는 볼록한 균일한 벌집 중 3개와 볼록한 균일한 4-폴리토프 중 9개에서 세포로 나타납니다.

정육면체의 부피는둘러싸는 입방체의 5/6 및 둘러싸는 팔면체의 5/8.

정점 배치

정육면체의 중심은 반지름적으로 등각이기 때문에 정육면체의 중심은 정육면체의 다른 정점에서 한 모서리 길이만큼 떨어져 있는 13번째 정육면체의 정점으로 취급될 수 있다.

정육면체는 볼록하지 않은 두 개의 다면체와 모서리와 정점 배치를 공유한다: 정육면체(정육면체를 공통으로 함)와 정육면체(정삼각형 면을 공통으로 함)는 둘 다 4개의 육면체를 가지고 있다.그것은 또한 정류된 사면체로서 캔텔레이트된 사면체 역할을 한다.

육팔면체	그 적도	입방정체	팔면체

정육면체는 2개의 정육면체를 ^[5]덮고 있으며, 이에 따라 추상적인 정점 도형(2개의 삼각형과 2개의 정사각형: 3.4.3.4)과 정점, 모서리 및 면의 절반이 있습니다.(사십육면체의 실제 꼭지점 도형은 3.4.3/2.4이며, a/2 인자는 십자가로 인한 것입니다.)

육팔면체	사십육면체

운동학

8면체, 의사이십면체, 정육면체 사이의 진행입니다.정육면체는 모서리(면이 아님)가 단단하더라도 이러한 방식으로 구부릴 수 있습니다.

경첩에 의해 모서리를 따라 연결된 단단한 평면 골격으로 해석될 때, 정육면체는 코시의 정리에 의해 모두 볼록한 다면체와 마찬가지로 단단한 구조이다.그러나 면이 제거되고 정점에서 유연한 조인트로 연결된 강체 가장자리만 남게 되면, 그 결과는 강체 시스템이 아닙니다(면이 모두 삼각형인 다면체와 달리, 면이 누락됨에도 불구하고 코치의 정리가 적용됩니다).

다른 모든 정점에 단단한 모서리로 연결된 중앙 정점을 추가하면 정육면체가 중앙 정점에서 만나는 정사각형 피라미드와 사면체로 세분됩니다.정육면체 자체와 달리 모서리와 접합부의 결과 시스템은 강성이며 무한 옥텟 트러스 구조의 일부를 형성합니다.

정육면체 그래프

그래프 이론의 수학 분야에서, 정육면체 그래프는 아르키메데스의 고체 중 하나인 정육면체의 정점과 모서리의 그래프이다.큐브의 선 그래프로 구성할 수도 있습니다.12개의 꼭지점과 24개의 모서리가 있고 국소적으로 선형이며 4차 아르키메데스 ^[8]그래프입니다.

직교 투영
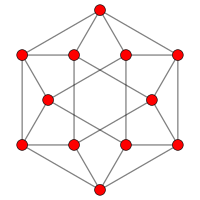6배 대칭

문화적 사건

이스라엘 굴뚝에 2개의 큐브옥타헤드라.

스타트렉 에피소드 "By Any Other Name"에서 외계인들은 승무원을 무생물 큐빅타헤드라로 변형시켜 엔터프라이즈를 점령한다.
"지오 트위스터" 피젯 장난감은 유연한 정육면체입니다.
컴퓨터 게임 시리즈인 Elite에 나오는 코리올리 우주 정거장은 정육면체 모양이다.
Vesak Poya의 날을 기념하기 위해 스리랑카에서 매년 만들어지는 전통 등불인 Vesak Kuudu는 보통 정사각형이다.
슈퍼 마리오 ^[9]오디세이의 '문스네이크스'
InfluentDB 시계열 데이터베이스 뒤에 있는 회사 InfluentData는 로고에 정육면체를 사용합니다.
2021년 아이작 아시모프 파운데이션 시리즈의 '프라임 레이디언트'는 회로 패턴이 있는 투명한 정육면체이다.

「」를 참조해 주세요.

메모들

^ 정육면체는 서로 60° 기울어진 4개의 육각형 중심 평면을 가지고 있습니다.육각형과 같이, 정팔면체는 그 중심에서 만나는 정삼각형으로 나눌 수 있다: 그것은 반지름 정삼각형 대칭을 가지고 있다.

레퍼런스

^ 콕서터 1973, 18-19페이지, § 2.3 준정규 다면체.
^ Heath, Thomas L. (1931), "A manual of Greek mathematics", Nature, Clarendon, 128 (3235): 739–740, Bibcode:1931Natur.128..739T, doi:10.1038/128739a0, S2CID 3994109
^ "Vector Equilibrium: R. Buckminster Fuller".
^ 콕서터 1973, 페이지 52, §3.7 정규 및 준정규 고체의 정점에 대한 좌표.
^ Richter, David A., Two Models of the Real Projective Plane, archived from the original on 2016-03-03, retrieved 2010-04-15
^ 콕서터 1973, 페이지 86-88, § 5.7 위토프의 구조.
^ 다니엘 휴슨의 2차원 대칭 돌연변이
^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
^ "File:Moonsnake Icon SMO.png - Super Mario Wiki, the Mario encyclopedia". www.mariowiki.com. Retrieved 2018-11-05.

참고 문헌

Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
Ghyka, Matila (1977). The geometry of art and life ([Nachdr.] ed.). New York: Dover Publications. pp. 51–56, 81–84. ISBN 9780486235424.
Weisstein, Eric W. (2002). "Cuboctahedron". CRC Concise Encyclopedia of Mathematics (2nd ed.). Hoboken: CRC Press. pp. 620–621. ISBN 9781420035223.
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3절부터 제9절까지)
Cromwell, P. Polyedra, CUP hbk(1997), pbk(1999).제2장 79-86 아르키메데스의 고체

외부 링크

통일된 다면체
가상현실 폴리헤드라 폴리헤드라 백과사전
Eric W. Weisstein, Cuboctahedron (Archimedean solid) at MathWorld.
육각형 수학 전문 사이트인 헥스넷의 육면체.
Klitzing, Richard. "3D convex uniform polyhedra o3x4o - co".
대화형 3D 뷰가 있는 육면체의 편집 가능한 그물망

[5] 정육면체는 서로 60° 기울어진 4개의 육각형 중심 평면을 가지고 있습니다.육각형과 같이, 정팔면체는 그 중심에서 만나는 정삼각형으로 나눌 수 있다: 그것은 반지름 정삼각형 대칭을 가지고 있다.

[FOOTNOTECoxeter197318–19§2.3_Quasi-regular_polyhedra-1] 콕서터 1973, 18-19페이지, § 2.3 준정규 다면체.

[2] Heath, Thomas L. (1931), "A manual of Greek mathematics", Nature, Clarendon, 128 (3235): 739–740, Bibcode:1931Natur.128..739T, doi:10.1038/128739a0, S2CID 3994109

[3] "Vector Equilibrium: R. Buckminster Fuller".

[FOOTNOTECoxeter197352§3.7_Coordinates_for_the_vertices_of_the_regular_and_quasi-regular_solids-4] 콕서터 1973, 페이지 52, §3.7 정규 및 준정규 고체의 정점에 대한 좌표.

[richter-6] Richter, David A., Two Models of the Real Projective Plane, archived from the original on 2016-03-03, retrieved 2010-04-15

[FOOTNOTECoxeter197386–88§5.7_Wythoff's_construction-7] 콕서터 1973, 페이지 86-88, § 5.7 위토프의 구조.

[8] 다니엘 휴슨의 2차원 대칭 돌연변이

[9] Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269

[10] "File:Moonsnake Icon SMO.png - Super Mario Wiki, the Mario encyclopedia". www.mariowiki.com. Retrieved 2018-11-05.

[1]

[2]

[3]

[4]

[a]

[5]

[6]

[7]

[8]

[9]

균일한 팔면체 다면체
대칭: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= 또는	= 또는	=

이중에서 균일한 다면체
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

균일한 사면체 다면체군
대칭 : [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
이중에서 균일한 다면체

V3.3.3	V3.6.6	V3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

*n32 준규형 타일링의 오비폴드 대칭: (3.n)²
건설	구면			유클리드	쌍곡선
건설	*332	*432	*532	*632	*732	*832...	*∞32
준규격 수치
꼭지점	(3.3)²	(3.4)²	(3.5)²	(3.6)²	(3.7)²	(3.8)²	(3.²199)

*n42 준규격 타일링 대칭 돌연변이: (4.n)² v t
대칭 *4n2 [n,4]	구면	유클리드	콤팩트 쌍곡선				파라콤팩트	콤팩트하지 않다
대칭 *4n2 [n,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[니,4]
수치
설정.	(4.3)²	(4.4)²	(4.5)²	(4.6)²	(4.7)²	(4.8)²	(4.²199)	(4.ni)²

*n32 확장타일링 대칭 돌연변이 : 3.4.n.4
대칭 *n32 [n,3]	구면				유클리드	콤팩트 쌍곡선		파라콤프
대칭 *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
그림
설정.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Search

육팔면체

네임스페이스

더

목차

동의어

직교 투영

구면 타일링

구조.

좌표

루트 벡터

메트릭 속성

절개요

정팔면체와 정팔면체

불규칙 다면체

기하 관계

반지름 등변 대칭

구성

정점 배치

운동학

관련 폴리토프

정다면체

준규격 다면체 및 타일링

4차원 폴리토프

정육면체 그래프

문화적 사건

「」를 참조해 주세요.

메모들

레퍼런스

참고 문헌

외부 링크

Search

육팔면체

동의어

직교 투영

구면 타일링

구조.

좌표

루트 벡터

메트릭 속성

절개요

정팔면체와 정팔면체

불규칙 다면체

기하 관계

반지름 등변 대칭

구성

정점 배치

운동학

관련 폴리토프

정다면체

준규격 다면체 및 타일링

4차원 폴리토프

정육면체 그래프

문화적 사건

「 」를 참조해 주세요.

메모들

레퍼런스

참고 문헌

외부 링크

「」를 참조해 주세요.