폴라니 이론
Potential theory of Polanyi폴라니 흡착 전위론이라고도 불리는 폴라니 전위론은 표면 가까이에 있는 기체의 화학적 전위와 멀리 떨어진 기체의 화학적 전위 사이의 평형을 통해 흡착을 측정할 수 있는 마이클 폴라니에 의해 제안된 흡착의 모델이다. 그는 이 모델에서 기체의 표면으로의 반 데르발스 힘에 의한 유인력은 주로 표면에서 나오는 기체 입자의 위치에 의해 결정되며, 기체가 평형 증기 압력을 초과하는 응축까지 기체가 이상적인 기체로 작용한다고 가정했다. Henry의 흡착 이론은 저압에서 더욱 적용가능하고 BET 흡착 등식은 0.05 - 0.35 P/Po에서 더 유용하지만, Polanyi 전위 이론은 P/Po (~0.1–0.8)에서 훨씬 더 많이 적용된다.
개요
마이클 폴라니
마이클 폴라니(Michael Polanyi, FRS, 1891년 3월 11일 ~ 1976년 2월 22일)는 헝가리의 다산수학으로, 물리 화학, 경제, 철학에 이론적 공헌을 하였다. 폴라니는 고체에 가스를 흡착하는 것, 고체의 성질에 대한 X선 구조 분석, 화학 반응 속도 등 세 가지 주요 연구 분야를 통해 화학 분야에 공헌한 유명한 이론 화학자였다. 그러나 폴라니 교수는 화학 분야 내에서 이론적 연구와 실험적 연구에 모두 적극적이었다. 폴라니 교수는 부다페스트 대학에서 1917년 물리화학 박사학위를 취득한 것은 물론 1913년 의학박사학위를 취득했다. 말년에 그는 영국 맨체스터 대학뿐만 아니라 베를린의 카이저 빌헬름 연구소에서 화학 교수로 가르쳤다.
역사
제안 이론
1914년, 폴라니는 흡착에 대한 그의 첫 번째 논문을 썼다. 그는 단단한 표면에 가스를 흡착하는 모델을 제안했다.[1] 그 후 1916년에 완전히 개발된 논문을 발표하였는데, 이 논문에는 제자들과 다른 저자들의 실험적인 검증이 포함되어 있었다. 부다페스트 대학교에서 그의 멘토인 게오르크 브레디그 교수는 그의 연구 결과를 알버트 아인슈타인에게 보냈다. 아인슈타인은 브레디그에게 다음과 같이 답장을 썼다.
너의 M. 폴라니 신문이 나를 많이 기쁘게 해 줘. 나는 그 안에 있는 필수품들을 확인했고 그것들이 근본적으로 옳다는 것을 알았다.
폴라니는 나중에 이 사건을 다음과 같이 설명하였다.
쾅! 나는 과학자였다.
폴라니와 아인슈타인은 그 후 20년 동안 계속해서 서로에게 편지를 썼다 하지 않았다.
비판
폴라니의 흡착 모델은 출판된 지 몇 년이 지난 후 수십 년 동안 많은 비난을 받았다. 그의 흡착판단을 위한 단순화된 모델은 보어의 원자 모델인 데비의 고정된 이중돌기가 발견되고 W.H. Bragg, W.L.Bragg, Willem Hendrik Keesom 등 화학계의 주요 인물들에 의한 분자간력과 정전기력의 발전 이론이 발견되는 시기에 형성되었다. 그의 모델에 반대하는 사람들은 폴라니 이론이 이러한 신흥 이론들을 고려하지 않았다고 주장했다. 비판에는 모델이 기체와 표면의 전기적 상호작용을 고려하지 않았으며, 다른 분자의 존재는 기체의 표면으로의 흡인을 차단할 것이라는 점이 포함되었다. 폴라니의 모델은 1916년부터 1918년까지 어빙 랑무르의 실험적인 주장에 따라 더욱 정밀하게 검토되었다. 그의 연구는 결국 1932년에 노벨상을 수상하게 될 것이다. 그러나 폴라니는 제1차 세계대전 당시 세르비아 전선에서 오스트리아-헝가리군의 의병장교로 근무했기 때문에 이러한 논의에 많은 참여를 할 수 없었다.폴라니는 이 경험에 대해 다음과 같이 적었다.
나 자신도 1914년 8월부터 1918년 10월까지 오스트리아-헝가리군에서 의병으로 복무하고, 1919년 말까지 지속된 뒤이은 혁명과 반혁명으로 이러한 전개에 대한 어떠한 지식으로부터도 한동안 보호를 받았다. 다른 곳에서는 지식이 부족한 서클의 회원들은 내 이론의 단순함과 넓은 실험 검증에 한동안 감명을 받았다.[1]
방어
폴라니 교수는 독일 베를린의 카이저 빌헬름 물리화학연구소에서 프리츠 하버가 자신의 이론을 전면적으로 옹호해 달라고 요청하면서 자신의 흡착 모델을 수용하는 '터닝 포인트'가 발생했다고 설명했다. 이번 회의에는 알버트 아인슈타인을 비롯해 과학계의 주요 인사들이 대거 참석했다. 그의 모델에 대한 폴라니의 충분한 설명을 들은 후, 하버와 아인슈타인은 폴라니가 "과학적으로 확립된 문제의 구조에 대해 완전히 무시하는 태도를 보였다"고 주장했다. 몇 년 후, 폴라니 씨는 자신의 시련을 결론짓고 설명했다.
직업상, 나는 간신히 그 기회를 견뎌냈다.
폴라니는 이 회의가 끝난 후 자신의 모델 연도의 타당성을 입증하는 데 있어서 계속적인 근거를 제시하였다.[1]
리퓨테이션
폴라니(Polanyi)가 자신의 모델에 대한 이러한 거부와 비판으로부터 얻은 '전달(deliverance)'은 프리츠 런던이 전자 시스템의 양극화에 관한 양자역학 이론에 기초하여 새로운 응집력 이론을 제안하면서 1930년에 일어났다. 폴라니는 런던에 편지를 써서 이렇게 물었다.
"이러한 힘들이 분자를 개입시켜 선별의 대상이 되는가? 이러한 힘에 의한 탄탄한 연기가 공간적으로 고정된 흡착 잠재력을 가질 수 있을까?"
컴퓨터 분석 후, 폴라니와 런던 사이에 흡착력이 폴라니시가 제안한 모델과 유사하게 행동했다고 주장하는 공동 출판물이 만들어졌다.[1]
추가 연구
폴라니의 이론은, 볼륨 채우기 마이크로포어(TVFM) 이론과 두비닌-라두슈케비치 이론과 같은 다른 모델의 기초가 되어온 저작의 역사적 의의를 가지고 있다. 지그몬디가 발견한 모세관 응축현상과 같은 폴라니의 잠재 이론을 느슨하게 포함하는 다른 연구도 수행되었다. 평평한 표면을 포함하는 Poylani의 이론과 달리, Zsigmondy의 연구는 실리카 물질과 같은 다공성 구조를 포함한다. 그의 연구는 표준 포화 증기 압력 이하의 좁은 모공에서 증기 응결이 발생할 수 있다는 것을 증명했다.[2]
이론
폴라니 잠재적 흡착 이론
폴라니 전위 흡착 이론은 표면 근처의 분자들이 중력이나 전기장의 그것과 유사하게 전위에 따라 움직인다는 가정에 근거한다.[3] 이 모델은 일정한 온도에서 표면의 기체의 경우에 적용된다. 가스 분자는 압력이 평형 증기 압력보다 높을 때 그 표면으로 더 가까이 이동한다. 표면으로부터의 거리에 따른 전위 변화는 화학적 전위차이에 대한 공식으로 계산할 수 있다.
여기서 은(는 화학전위, {\ S_은(는) 어금니 엔트로피, {\displaystyle {은(는)은 어금니 체적, 은 어금니 내부 에너지.
평형상태에서 표면으로부터 거리 ( , ) (initely ,) ,p 그 결과 통합이 된다. 무한히 먼 거리에서부터 표면으로부터 r까지의 거리까지가 ~로 이어진다.
여기서 는 r 거리의 부분 압력이고 은 표면으로부터 무한히 떨어진 곳의 부분 압력이다.
온도가 일정하게 유지되기 때문에 화학적 전위 공식의 차이는 p 과 r 에 걸쳐 통합될 수 있다.
)= 을 설정함으로써 방정식을 다음과 같이 단순화할 수 있다
이상적인 가스 법칙을 사용하여 = 다음 공식을 구함
기체의 압력이 평형증기압력 p 을 초과할 때 기체가 표면의 액체로 응축되기 때문에 두께의 표면 위에 액체 필름이 형성된다고 가정할 수 있다
기체의 부분압력이 농도와 관련됨을 감안하여 흡착전위 s 을(를) 다음과 같이 계산할 수 있다.
여기서 은(는) 흡착제의 포화 농도, 은 흡착제의 평형 농도다.
폴라니 흡착 이론에 근거한 이론
그 잠재 이론은 첫 보고서 이후 여러 해 동안 많은 개선과 변화를 겪었다. 폴라니 이론을 이용하여 개발된 대표적인 이론 중 하나는 두비닌 이론, 두비닌-라두시키베흐, 두비닌-아스타호프 방정식이었다.
흡착 전위를 사용하여 공간의 충전 정도인 , 을를) 다음과 같이 계산할 수 있다.
서 은 온도 T와 평형 압력 p에서의 흡착 값이고, 은 흡착의 최대값이며, 은 kJ/mol에서의 흡착의 특성 에너지, 은 흡착 시 Gibs 자유 에너지 손실이다. G=- T log 0/ p) G와 이(가) 적합 계수다.[4] 이(가) 2인 Dubinin-Radushkivech 방정식과 이(가) 실험 데이터에 적합한 최적화된 Dubinin-Astakhov 방정식을 다음과 같이 단순화할 수 있다.
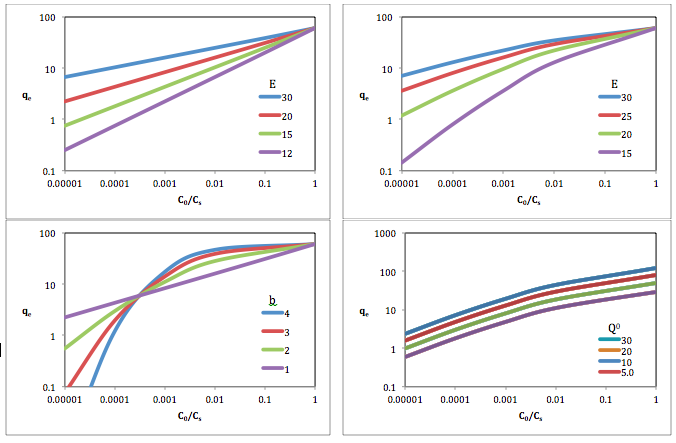
다른 연구에서는 유사한 형태의 e = 로그 0+ (w / ) {\log Q^{0
where is equilibrium adsorbed concentration of adsorbent in mg/g, is maximum adsorbed concentration of adsorbent in mg/g, is the effective adsorption potential, where equal to , is equilibrium concentration of adsorbent in the solution phase in mg/L, and is the adsorbent solubility in water in mg/L.[5]
흡착의 특성 에너지는 친화 계수 를 사용하여 동일한 표면의 표준 증기에 대한 흡착 특성 에너지인 E displaystyle E_{0과 관련될 수 있다
선호도 계수는 샘플과 표준 증기의 속성의 비율이다.
여기서 과(와) 은 각각 표본과 표준 증기의 편광성이다. 고형물에 가스와 증기의 흡착을 가장 잘 설명하기 위해 의 적합 계수 b 및 친화 계수 \beta 을(를 결정하기 위해 많은 연구가 수행되었다. 그 결과, 두비닌-아스타호프 방정식은 실험 결과가 적합되었을 때 얻을 수 있는 정확도로 인해 흡착 연구에서 계속 사용되고 있다.
증기 및 가스에 대한 두비닌-아스타호프 매개변수
| 화합물 | 활성탄 | E E kJ/mol | 출처 | ||
|---|---|---|---|---|---|
| 벤젠 | 탄소분자체 | 1.78 | 11.52 | 1.00 | [6] |
| 아세톤 | 탄소분자체 | 2.00 | 9.774 | 0.85 | [6] |
| 벤젠 | CAL AC | 2 | 18.23 | 1.00 | [7] |
| 아세톤 | CAL AC | 2 | 13.21 | 0.72 | [7] |
| 아세톤 | 탄소분자체 | 2.8 | 20.29 | 0.72 | [8] |
| 벤젠 | 탄소분자체 | 3.1 | 28.87 | 1.00 | [8] |
| 질소 | 탄소분자체 | 2.6 | 11.72 | 0.41 | [8] |
| 산소 | 탄소분자체 | 2.3 | 9.21 | 0.32 | [8] |
| 수소 | 탄소분자체 | 2.5 | 5.44 | 0.19 | [8] |
적용
많은 현대 연구에서, 폴라니 이론은 활성탄, 즉 탄소 흑색 연구에 널리 사용된다. 이 이론은 활성탄소의 기체 흡착과 비이온성 다순환 방향족 탄화수소의 흡착 과정과 같은 다양한 시나리오를 모델링하는데 성공적으로 사용되었다.[9] 이후 실험에서도 페놀이나 아닐린과 같은 이온성 다순환 방향족 탄화수소를 모델링할 수 있다는 것이 밝혀졌다. 보다 최근에, 폴리아니 흡착은 탄소 나노입자의 흡착을 모델링하는 데 사용되었다.
탄소 나노입자의 특성화
역사적으로, 이 이론은 통일된 흡착제와 다중 성분 솔루트를 모형화하는 데 사용되었다. 특정 쌍의 흡착제와 흡착제의 경우, 폴리아니 이론의 수학적 매개변수는 흡착제와 흡착제의 물리화학적 특성과 관련될 수 있다. 이 이론은 탄소 나노튜브와 탄소 나노입자의 흡착을 모형화하는 데 사용되었다. 양과 싱이 수행한 연구에서 이 이론은 랑무르, 프룬드리히, 칸막이보다 흡착성에 더 잘 맞는 것으로 밝혀졌다.[5] 그 실험은 탄소 나노입자와 탄소 나노튜브에 유기 분자의 흡착을 연구했다. 폴리아니 이론에 따르면 탄소 나노입자의 표면 결함 곡선은 흡착에 영향을 미칠 수 있다. 입자의 평평한 표면은 더 많은 표면 원자들이 유기 분자를 흡착하는 것에 접근하게 할 것이고, 이것은 잠재력을 증가시켜 더 강한 상호작용을 이끌 것이다. 그 이론은 탄소 나노입자에 유기 화합물의 흡착 메커니즘을 이해하려고 노력하고 흡착 용량과 친화력을 추정하는데 유익했다. 이 이론을 이용하여, 연구원들은 탄소 나노입자를 환경 연구에서 흡착제로 사용하는 것과 같은 특정한 요구에 맞게 설계할 수 있기를 바라고 있다.
서로 다른 시스템에서의 흡착
Manes, M, & Hofer, L. J. E.에 의해 시행된 이전의 연구들 중 하나에서,[10] 다양한 범위의 유기 용제를 사용하는 다양한 농도의 활성 탄소의 액체 위상 흡착 이소체를 특성화하는 데 Polyani 이론을 사용했다. 폴리아니 이론은 이러한 다양한 시스템에 잘 맞는 것으로 나타났다. 그 결과 때문에, 이 연구는 최소의 데이터를 사용하여 유사한 시스템에 대한 등가선 예측 가능성을 도입했다. 단, 다양한 용매에 대한 흡착은 제한된 범위에서만 적합할 수 있다는 것이 한계다. 그 곡선은 고용량 범위에서 데이터를 맞출 수 없었다. 이 연구는 또한 결과에 몇 가지 이상 징후가 있었다고 결론지었다. 활성탄에 대한 탄소 테트라클로라이드, 사이클로헥산, 이황화 탄소로부터의 흡착은 곡선에 잘 맞지 않았으며, 설명되어야 할 것으로 남아있다. 실험을 진행한 연구진은 테트라클로로이드와 시클로헥산 탄소의 강직 효과가 작용했을 것으로 추측하고 있다. 이 연구는 물 용액에서 나오는 유기액과 물 용액에서 나오는 유기 고형물과 같은 다양한 시스템으로 수행되었다.
경쟁적 흡착
다양한 시스템이 조사되었기 때문에 혼합 용액의 개별 흡착을 조사하기 위한 연구가 수행되었다. 이러한 현상을 경쟁적 흡착이라고도 하는데, 이는 솔루트가 동일한 흡착 사이트에서 경쟁하는 경향이 있기 때문이다. 로제네와 마네스의 실험에서 포도당, 요소, 벤조산, 프탈라이드, p-니트로페놀의 경쟁적 흡착이 있었다.[11] 그들은 폴라니 흡착 모델을 사용하여 활성탄 표면에 대한 각 화합물의 상대 흡착을 계산할 수 있었다.
참고 항목
참조
- ^ a b c d Polanyi, M (1963). "The Potential Theory of Adsorption". Science. 141 (3585): 1010–013. Bibcode:1963Sci...141.1010P. doi:10.1126/science.141.3585.1010. PMID 17739484.
- ^ http://web.iitd.ac.in/~arunku/파일/CEL311_Y13/Adsorption%20 Theory%20to%20 practice_Dabrowski.pdf
- ^ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2003). "Physics and Chemistry of Interfaces": 193–195.
{{cite journal}}: Cite 저널은 필요로 한다.journal=(도움말) - ^ Dubinin, M. M.; Astakhov, V. A. (1971). "Development of the Concepts of Volume Filling of Micropores in the Adsorption of Gases and Vapors by Microporous Adsorbents". Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science. 20 (1): 3–7. doi:10.1007/bf00849307.
- ^ a b Yang, K.; Xing, B. (2010). "Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application". Chemical Reviews. 110 (10): 5989–6008. doi:10.1021/cr100059s. PMID 20518459.
- ^ a b Doong, S. J.; Yang, R. T. (1988). "A simple potential theory model for predicting mixed-gas adsorption". Industrial & Engineering Chemistry Research. 27 (4): 630–635. doi:10.1021/ie00076a017.
- ^ a b Tamon, H.; Okazaki, M. (1996). "Influence of acidic surface oxides of activated carbon on gas adsorption characteristics". Carbon. 34 (6): 741–746. doi:10.1016/0008-6223(96)00029-2.
- ^ a b c d e Kawazoe, K.; Kawai, T.; Eguchi, Y.; Itoga, K. (1974). "Correlation of adsorption equilibrium data of various gases and vapors on molecular-sieving carbon". Journal of Chemical Engineering of Japan. 7 (3): 158–162. doi:10.1252/jcej.7.158.
- ^ Yang, K.; Wu, W.; Jing, Q & Zhu, L. (2008). "Aqueous adsorption of aniline, phenol, and their substitutes by multi-walled carbon nanotubes". Environmental Science and Technology. 42 (21): 7931–6. Bibcode:2008EnST...42.7931Y. doi:10.1021/es801463v. PMID 19031883.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Manes, M.; Hofer, B.J.E. (1969). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon". The Journal of Physical Chemistry. 73 (3): 584–590. doi:10.1021/j100723a018.
- ^ Manes, M.R.; Manes, M. (1976). "Application of the Polanyi adsorption potential theory to adsorption from solution on activated carbon. VII. Competitive adsorption of solids from water solution". The Journal of Physical Chemistry. 80 (9): 953–959. doi:10.1021/j100550a007.


 (는
(는 (는)
(는)  (는)은 어금니
(는)은 어금니  어금니
어금니 



 r 거리의
r 거리의  표면으로부터 무한히 떨어진 곳의 부분 압력이다.
표면으로부터 무한히 떨어진 곳의 부분 압력이다. 









 (는) 흡착제의 포화 농도,
(는) 흡착제의 포화 농도,  흡착제의 평형 농도다.
흡착제의 평형 농도다. 

 온도 T와 평형 압력 p에서의 흡착 값이고,
온도 T와 평형 압력 p에서의 흡착 값이고,  흡착의 최대값이며,
흡착의 최대값이며,  kJ/mol에서의 흡착의 특성 에너지,
kJ/mol에서의 흡착의 특성 에너지,  흡착 시
흡착 시 
 (가) 적합 계수다.
(가) 적합 계수다.









 (와)
(와) 





