그리드 생성 원리

격자 또는 메시는 물리적 영역을 포괄하는 작은 크기의 이산형 셀로서, 보존 법칙이 적용될 수 있는 이산형 볼륨이나 원소를 식별하는 것이 목적이다.그들은 부분 미분방정식(PDE)에 대한 수치적 해법이 필요한 많은 장소, 지역, 설계 및 컴퓨터 유체역학(CFD), 응용 분야를 가지고 있다.

수치 그리드 생성은 물리적 프로세스를 기술하는 방정식에 대한 수치 해법 계산에 관련된 중요한 초기 단계다.용액의 정확도는 생성된 그리드의 품질에 따라 달라진다.잘 구성된 그리드는 용액의 품질을 개선할 수 있는 반면, 제대로 구성되지 않은 그리드에서 수치 해법으로부터의 편차를 관찰할 수 있다.셀을 만드는 기술은 그리드 생성의 기초를 형성한다.그리드 생성을 위한 다양한 방법이 아래에 설명되어 있다.

대수법

노즐 기하학

물리적 공간의 연산 메시

대수적 방법에 의한 격자 발생은 수학적 보간 함수에 기초한다.그것은 알려진 기능을 1, 2, 3차원에서 임의의 형상을 가진 지역을 취함으로써 이루어진다.계산 도메인은 직사각형이 아닐 수 있지만 단순성을 위해 직사각형으로 간주된다.이 방법의 주요 장점은 물리적 격자 모양과 간격을 명시적으로 제어할 수 있다는 것이다.경계 맞춤 계산 메쉬를 생산하는 데 사용할 수 있는 가장 간단한 절차는 정규화 변환이다.^[1]
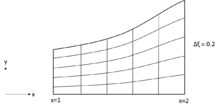
노즐의 경우, 설명 $y=x^{2}$ y = $y=x^{2}$ 2 ${\$ y= $x^{2$ }}로 x 방향으로 균일한 간격으로 분할하여 그리드를 $y=x^{2}$ 쉽게 생성할 수 있으며, 이는 다음과 같이 설명된다.

\displaystyle \xi =x\,}

\eta ={\frac {y}{y_{\max}}\,

여기서 $y_{\max }$ $y_{\max }$ ${\$ 은 노즐 벽의 y-through를 나타낸다 $y_{\max }$ . $\eta$ 값( $\$ {\ $displaystyle \xi$ }, $\$ {\ $displaystyle \eta })$ 의 경우 ( $x$ ${\displaystyle x$ $y$ ${\displaysty y$ 을 쉽게 복구할 수 있다.

미분방정식법

대수적 방법과 마찬가지로 격자 생성에도 미분방정식이 사용된다.부분 미분방정식(PDE)을 사용할 경우의 이점은 그리드 생성 방정식의 솔루션을 이용하여 메쉬를 생성할 수 있다는 것이다.그리드 구성은 세 가지 등급의 부분 미분 방정식을 모두 사용하여 수행할 수 있다.

타원체

타원형 PDE는 일반적으로 부드러운 등고선으로 이어지는 매우 부드러운 용액을 가지고 있다.그것의 부드러움을 장점으로 사용하는 것은 제이코비안이 조화 함수에 대한 최대 원리의 결과로 양성이라는 것을 알았기 때문에 라플레이스의 방정식을 사용하는 것이 바람직할 수 있다.톰슨 외 연구진(1974)은 포아송의 방정식을 이용하여 매핑하면서 물리적 영역을 계산면으로 변형시켜 PDE에 대해 크롤리(1962)와 윈슬로우(1966)가 ^[2]수행한 광범위한 작업을 거쳐 타원형 PDE에 광범위하게 연구해 그리드를 생성해 왔다.^[3]포아송 그리드 생성기에서 매핑은 물리적 영역의 경계에 원하는 $(x,y)$ 그리드 포인트 $(x,y)$ , y $(x,y)$ ) ${\displaystyle(x,y)}$ 을(를) 표시하여 수행되며, 내부 포인트 분포는 아래에 기재된 방정식의 솔루션을 통해 결정된다.

\xi _{xx}+\xi _{yyy}=P(\xi ,\eta )

\eta \{x}+\eta _{yyy}=Q(\xi,\eta )

여기서, ( $(\xi ,\eta )$ , $(\xi ,\eta )$ ) $(\xi ,\eta )$ 은 계산 영역의 좌표인 $(\xi ,\eta )$ 반면, P와 Q는 D 내의 점 간격을 담당한다.계산 공간에서 위의 방정식을 변환하면 두 개의 타원형 PDE가 생성된다.

\alpha x_{\xi \xi }-2\beta x_{\xi \eta }+\gamma x_{\eta }=-I^{2}(Px_{\xi }}+Qx_{\eta }}}}}}

{\displaystyle \alpha y_{\xi \}-2\beta y_{\xi \eta }+\gamma y_{\eta }=-I^{2}(Py_{\xi }}}+Qy_{\eta }}})

어디에

{\begin{aligned}\alpha &=x_{\eta }^{2}+y_{\eta }^{2}\\\beta &=x_{\eta }x_{\xi }+y_{\xi }y_{\eta }\\\gamma &=x_{\xi }^{2}+y_{\xi }^{2}\\I&={\frac {\delta (x,y)}{\delta (\xi ,\eta )}}}=y_{\eta }x_{\xi }-y_{\xi }{\x_{\eta }\ended}}}}}}}}}}}

이러한 방정식의 시스템은 물리적 공간에 있는 각 점의 $(x,y)$ ( $(x,y)$ , $(x,y)$ ) $(x,y)$ 개의 $(x,y)$ 좌표를 제공하는 균일한 간격 격자의 계산면에서 해결된다.타원형 PDE를 사용할 때의 장점은 연결된 솔루션이 부드럽고 결과 그리드가 부드럽다는 것이다.그러나 P와 Q의 사양은 어려운 과제가 되어 그 단점을 가중시킨다.더욱이 그리드는 계산 시간이 더해지는 각 시간 단계 후에 계산되어야 한다.^[4]

쌍곡선 계획

이 그리드 생성 체계는 일반적으로 물리적 문제를 기술하는 PDE 유형과 일치하는 개방형 도메인 문제에 적용할 수 있다.쌍곡선 PDE와 관련된 이점은 그리드 생성을 위해 지배 방정식을 한 번만 해결하면 된다는 것이다.대략적인 경계 조건과 함께 초기 점 분포는 필요한 입력을 형성하며, 해결책은 바깥쪽으로 행군한다.스테거와 소렌손(1980)^[5]은 메쉬 생성을 위해 쌍곡성 PDE를 사용하는 볼륨 정형성 방법을 제안했다.2-D 문제의 경우 $\Delta \xi =\Delta \eta =1$ $\Delta \xi =\Delta \eta =1$ = $\Delta \xi =\Delta \eta =1$ η $\Delta \xi =\Delta \eta =1$ = $\Delta \xi =\Delta \eta =1$ $\Delta \xi =\Delta \eta =1$ 에 의해 주어질 계산 공간을 고려할 때 Jacobian의 역은 다음과 같다 $\Delta \xi =\Delta \eta =1$

x_{\xi }y_{\eta }-x_{\eta }y_{\xi }=I

여기서 $I$ $I$ 은(는) 계산 공간의 특정 영역에 대한 물리적 공간의 영역을 나타낸다 $I$ .두 번째 방정식은 다음과 같이 쓰여질 수 있는 물리적 공간의 경계에서 격자선의 직교성을 연결한다.

d\xi=0=\xi _{x}\,dx+\xi _{y}\,dy.}

$\xi$ ${\displaystyle \xi$ } $\eta$ { $\eta$ {\ $displaystyle \eta }$ 표면이 $\eta$ 수직이 되는 경우 방정식은

x_{\xi }x_{\eta }+y_{\xi }y_{\eta }=0.

그러한 방정식 시스템과 관련된 문제는 $I$ $I$ 의 사양이다 $I$ $I$ $I$ 을(를) 잘 선택하지 않으면 충격과 망사 전체에서 이 정보가 불연속적으로 전파될 $I$ 수 있다.메쉬는 직교하는 속도가 매우 빠른 반면, 이 방법은 장점으로 나타난다.

포물선 계획

해결 기법은 끝부분의 경계 조건을 만족시키는 초기 데이터 표면으로부터 용액을 진척시켜 쌍곡선 PDE와 유사하다.나카무라(1982)와 에드워즈(1985)는 포물선 그리드 생성을 위한 기본 아이디어를 개발했다.이 아이디어는 라플라스 또는 포아송 방정식을 사용하며 특히 타원적 행동을 제어하는 부분을 다룬다.초기 값은 표면 $\eta =0$ = 0 $\eta =0$ 을(를) 따라 점의 좌표로 $\xi$ , $\$ {\ $displaystyle \xi$ } 가장자리를 따라 경계 조건을 만족하는 물체의 외부 표면으로 용액을 전진시킨다.

그리드 간격 제어는 지금까지 제안되지 않았다.나카무라와 에드워즈, 균일하지 않은 간격을 이용해 그리드 제어가 이루어졌다.포물선 그리드 생성은 충격이나 불연속성이 발생하지 않고 그리드가 비교적 매끄러운 쌍곡선 그리드 생성에 비해 장점을 보여준다.그리드 포인트를 제어하기 위한 초기값의 사양과 단계 크기의 선택은 시간이 걸리지만, 이러한 기법은 친숙함과 경험을 얻을 때 효과적일 수 있다.

변동 방법

이 방법에는 격자 평활성, 직교성 및 체적 변동을 최소화하는 기법이 포함된다.이 방법은 수학적 플랫폼을 형성하여 그리드 생성 문제를 해결한다.이 방법에서 대체 그리드는 각 반복 후 새로운 메쉬에 의해 생성되며 역차법을 사용하여 그리드 속도를 계산한다.이 기법은 격자와 관련된 방정식을 풀기 위해 노력이 필요하다는 단점이 있는 강력한 기법이다.CPU 시간을 줄이는 통합을 최소화하기 위해 추가 작업이 필요했다.

비정형 그리드 생성

메쉬 생성을 참조하십시오.이 계획의 가장 중요한 점은 그리드를 자동으로 생성하는 방법을 제공한다는 것이다.이 방법을 사용하여 그리드를 요소의 표면에 따라 블록으로 분할하고 적절한 연결을 보장하기 위한 구조를 제공한다.데이터 흐름 해결기를 해석하기 위해 사용된다.구조화되지 않은 체계가 채용되었을 때, 주된 관심사는 사용자의 요구를 충족시키는 것이며, 이 작업을 수행하기 위해 그리드 생성기를 사용하는 것이다.구조화된 구조에서 정보 저장소는 그리드 대 그리드 대신 셀 대 셀이기 때문에 더 많은 메모리 공간이 필요하다.무작위 셀 위치 때문에 구조화되지 않은 상태의 해결사 효율은 구조화된 구조에 비해 낮다.^[6]

그리드 구축 시 유의해야 할 사항도 있다.고해상도 그리드 포인트는 정형화 및 비정형화 모두에 어려움을 야기한다.예를 들어, 경계층의 경우, 구조화된 구조는 흐름의 방향으로 긴 그리드를 생성한다.반면에 구조화되지 않은 그리드는 셀이 오류를 피하기 위해 가능한 한 정사각형이어야 하기 때문에 경계 층에서 더 높은 셀 밀도를 요구한다.^[7]

연결 정보

우리는 계산 메쉬에서 셀과 셀의 모든 이웃을 식별하기 위해 필요한 정보를 식별해야 한다.구조화되지 않은 그리드에 대해 원하는 임의의 지점을 찾을 수 있다.포인트 삽입 방식은 포인트를 독립적으로 삽입하기 위해 사용되며 셀 연결이 결정된다.이는 해당 점을 삽입할 때 식별할 수 있음을 시사한다.포인트가 삽입되면 새로운 연결을 설정하기 위한 논리가 결정된다.그리드 셀을 식별하는 그리드 포인트를 형성하는 데이터가 필요하다.각 셀이 형성되면 번호가 매겨지고 포인트가 정렬된다.게다가 이웃 세포 정보가 필요하다.

적응 그리드

이전 방법을 이용한 부분 미분방정식 해결의 문제점은 솔루션의 세부사항이 알려지기 전에 그리드를 구성하고 물리적 영역에 점을 분산시키는 것이다.그러므로 격자는 주어진 문제에 최선이 될 수도 있고 아닐 수도 있다.^[8]

용액의 정확도를 높이기 위해 적응 방법을 사용한다.적응법은 메쉬 미세화를 사용할 경우 'h' 방법, 그리드 포인트의 개수가 고정되어 재분배되지 않을 경우 'r' 방법, 유한 요소 이론에서 솔루션 구성의 순서를 증가시킬 경우 'p'라고 한다.등분포 방식을 사용하는 다차원 문제는 여러 가지 방법으로 달성할 수 있다.가장 이해하기 쉬운 것은 원하는 셀 볼륨의 배수로 설정된 확산과 무게 함수의 등분포를 기반으로 제어 기능을 가진 포아송 그리드 생성기다.등분포 방식은 구조화되지 않은 문제에도 적용될 수 있다.문제는 메쉬 포인트 이동이 매우 클 경우 연결성을 방해한다는 것이다.

꾸준한 흐름과 시간정확한 흐름 계산은 이 적응법을 통해 해결할 수 있다.그리드는 일정한 흐름 문제에서 조정하기 위해 미리 정해진 횟수의 반복 후에 정제된다.일단 용액이 수렴되면 그리드는 변화에 대한 조정을 중지할 것이다.적시에 물리적 문제의 부분 미분방정식과 격자 이동을 설명하는 방정식의 정확한 사례 결합이 필요하다.

참고 항목

참조

^ Anderson, Dale (2012). Computational Fluid Mechanics and Heat Transfer, Third Edition Series in Computational and Physical Processes in Mechanics and Thermal Sciences. CRC Press. pp. 679–712. ISBN 978-1591690375.
^ Winslow, A (1966). "Numerical Solution of Quasi-linear Poisson Equation". J. Comput. Phys. 1 (2): 149–172. doi:10.1016/0021-9991(66)90001-5.
^ Thompson, J.F.; Thames, F.C.; Mastin, C.W. (1974). "Automatic Numerical Generation of Body-fitted Curvilinear Coordinate System for Field Containing any Number of Arbitrary Two-Dimensional Bodies". J. Comput. Phys. 15 (3): 299–319. doi:10.1016/0021-9991(74)90114-4.
^ Young, David (1954). "Iterative methods for solving partial difference equations of elliptic type". Transactions of the American Mathematical Society. 76 (1): 92–111. doi:10.2307/1990745. ISSN 1088-6850. JSTOR 1990745.
^ Steger, J.L; Sorenson, R.L (1980). "Use of hyperbolic partial differential equation to generate body fitted coordinates, Numerical Grid Generation Techniques". NASA Conference Publication 2166: 463–478.
^ Venkatakrishnan, V; Mavriplis, D. J (May 1991). "Implicit solvers for unstructured meshes". Journal of Computational Physics. 105 (1): 23. doi:10.1006/jcph.1993.1055. hdl:2060/19910014812.
^ Weatherill, N.P (September 1992). "Delaunay triangulation in computational fluid dynamics". Computers & Mathematics with Applications. 24 (5–6): 129–150. doi:10.1016/0898-1221(92)90045-j.
^ Anderson, D.A; Sharpe H.N. (July 1993). "Orthogonal Adaptive Grid Generation with Fixed Internal Boundaries for Oil Reservoir Simulation". SPE Advanced Technology Series. 2. 1 (2): 53–62. doi:10.2118/21235-PA.

[1] Anderson, Dale (2012). Computational Fluid Mechanics and Heat Transfer, Third Edition Series in Computational and Physical Processes in Mechanics and Thermal Sciences. CRC Press. pp. 679–712. ISBN 978-1591690375.

[2] Winslow, A (1966). "Numerical Solution of Quasi-linear Poisson Equation". J. Comput. Phys. 1 (2): 149–172. doi:10.1016/0021-9991(66)90001-5.

[3] Thompson, J.F.; Thames, F.C.; Mastin, C.W. (1974). "Automatic Numerical Generation of Body-fitted Curvilinear Coordinate System for Field Containing any Number of Arbitrary Two-Dimensional Bodies". J. Comput. Phys. 15 (3): 299–319. doi:10.1016/0021-9991(74)90114-4.

[4] Young, David (1954). "Iterative methods for solving partial difference equations of elliptic type". Transactions of the American Mathematical Society. 76 (1): 92–111. doi:10.2307/1990745. ISSN 1088-6850. JSTOR 1990745.

[5] Steger, J.L; Sorenson, R.L (1980). "Use of hyperbolic partial differential equation to generate body fitted coordinates, Numerical Grid Generation Techniques". NASA Conference Publication 2166: 463–478.

[6] Venkatakrishnan, V; Mavriplis, D. J (May 1991). "Implicit solvers for unstructured meshes". Journal of Computational Physics. 105 (1): 23. doi:10.1006/jcph.1993.1055. hdl:2060/19910014812.

[7] Weatherill, N.P (September 1992). "Delaunay triangulation in computational fluid dynamics". Computers & Mathematics with Applications. 24 (5–6): 129–150. doi:10.1016/0898-1221(92)90045-j.

[8] Anderson, D.A; Sharpe H.N. (July 1993). "Orthogonal Adaptive Grid Generation with Fixed Internal Boundaries for Oil Reservoir Simulation". SPE Advanced Technology Series. 2. 1 (2): 53–62. doi:10.2118/21235-PA.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search