자기 에너지

양자장 이론에서 입자가 환경에 일으키는 변화의 결과로서 갖는 에너지는 자기 에너지 ${\displaystyle \Sigma }$를 정의하며 입자와 환경 사이의 상호작용에 의해 입자의 에너지, 즉 유효 질량에 대한 기여를 나타낸다. 전기 공학에서, 전하 분배를 조립하는 데 필요한 에너지는 전력이 0으로 가는 무한대에서 구성 전하를 가져옴으로써 자가 에너지의 형태를 취한다. 물질 내에서 움직이는 전자와 관련된 응축된 물질 맥락에서, 자기 에너지는 그것과 주변 매체의 상호 작용으로 인해 전자가 느끼는 전위를 나타낸다. 전자가 서로 밀어내기 때문에 움직이는 전자는 양극화되거나, 또는 그 근처에 있는 전자를 대체하게 한 다음 움직이는 전자장의 전위를 변화시킨다. 이것들과 다른 효과들은 자기 에너지를 수반한다.

특성.

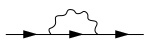
수학적으로 이 에너지는 모멘텀 에너지 표현에서 적절한 자기 에너지 연산자(또는 적절한 질량 연산자)의 소위 질량 쉘 값(또는 질량 연산자)과 같다(더 정밀하게 말하면 이 값의 $times$ ${\displaystyle \hbar }).$ 이것 또는 다른 표현(공간 표현과 같은)에서 자기 에너지는 아래 나온 것과 같이 파인만 도표를 통해 그림(그리고 경제적으로)으로 표현된다. 이 특정한 다이어그램에서, 화살표가 달린 세 개의 직선은 입자 또는 입자 전파기를 나타내며, 물결선은 입자와 입자 사이의 상호작용을 나타낸다. 아래 다이어그램에서 가장 왼쪽과 오른쪽 가장 오른쪽 직선을 제거(또는 절단)한다(이러한 외부 선들은 예를 들어, 모멘텀에 대해 규정된 값에 해당한다. 에너지(예: 모멘텀 에너지 표현)는 자가 에너지 운영자에 대한 기여도를 유지한다. 소수의 간단한 규칙을 사용하면 각 파인만 도표는 해당 대수적 형태로 쉽게 표현할 수 있다.

일반적으로 모멘텀 에너지 표현에서 자가 에너지 사업자의 질량 변화는 복잡하다. 이러한 경우 물리적 자기 에너지(위는 입자의 "자기 에너지"라고 함)와 동일시되는 것이 이 자기 에너지의 실제 부분이다. 상상의 부분의 역은 조사 중인 입자의 수명에 대한 측정이다. 명확성, 기초적 배설물 또는 복장 입자(준입자 참조)를 위해 상호 작용하는 시스템에서는 진공 상태의 안정적인 입자와 구별된다; 그들의 상태 기능은 기초적인 다입자 시스템의 고유체들의 복잡한 초상으로 구성된다. 이러한 초입자(multi-particle system)는 단지 순간적으로만 격리된 미립자 특유의 초입자처럼 작용한다.es; 위에서 언급한 수명은 복장을 한 입자가 잘 정의된 운동량과 에너지를 가진 하나의 입자인 것처럼 행동하는 시간이다.

The self-energy operator (often denoted by ${\displaystyle \Sigma _{}^{}}$, and less frequently by ${\displaystyle M_{}^{}}$) is related to the bare and dressed propagators (often denoted by ${\displaystyle G_{0}^{}}$ and ${\displaystyle G_{}^{}}$ respectively) via the Dyson equation (named 프리먼 다이슨 다음:

${\displaystyle G=G_{0}^{}+G_{0}\Sigma G.}$

${\displaystyle {\mathrm{왼쪽}}_{}^{}}$에는 연산자 $G{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$${\displaystyle {}_{}^{}}$${\$${0}^{1$}-1}의$$ 역 $G{\displaystyle {}_{}^{}}$ 0 - 1 {\displaystyle G_${0$}^{-1$}$과(와$$$$ 오른쪽에는 ${\displaystyle {\mathrm{G}}^{}}$- 1 ${\$G^{-$1}$

${\displaystyle \Sigma =G_{0}^{-1}-G^{-1}.}$

광자와 글루온은 질량을 얻지 못하는데, 게이지 대칭은 질량을 얻는 것을 막아주기 때문이다. 이것은 워드의 정체성의 결과물이다. W-boson과 Z-boson은 힉스 메커니즘을 통해 질량을 얻는다; 그들은 전기 약품 이론의 리노말화를 통해 대량 재호르몬화를 겪는다.

내부 양자수를 가진 중성입자는 가상 쌍생산을 통해 서로 섞일 수 있다. 이 현상의 일차적인 예는 중성 카온의 혼합이다. 적절한 단순화 가정 하에서 이것은 양자장 이론 없이 설명될 수 있다.

기타 용도

화학에서, 이온의 자기 에너지 또는 Born 에너지는 이온 자체의 장과 관련된 에너지다.^{[citation needed]}

고체 상태와 응축 물질 물리학 자가영역에서는 전자 대역 구조 계산에 기초하여 저 에너지 배설물을 상호작용하는 그린의 함수 방식과 그린의 함수(다체 이론)에 의해 무수히 관련된 퀘이픽자 속성을 계산한다. 자기 에너지는 또한 개방형 양자 시스템을 통한 입자 전송의 계산과 더 큰 시스템(예를 들어 반무한 결정의 표면)에 하위 영역을 내장하는 데 광범위하게 응용되는 것을 발견한다.^{[citation needed]}

참고 항목

• 양자장 이론
• QED 진공 청소기
• 리노말화
• 자력
• GW 근사치
• 휠러-파인만 흡수기 이론

참조

• A. L. Fetter와 J. D. Walecka, Multi-Particle Systems의 양자 이론(McGraw-Hill, 1971년 뉴욕 주); (Dover, New York, 2003년)
• J. W. 네겔레 및 H. Orland, Quantum Multi-Particle Systems (Westview Press, Boulder, 1998)
• A. A. Abrikosov, L. P. Gorkov 및 I. E. Djyalosinski(1963): 통계물리학 잉글우드 절벽에서 양자장 이론의 방법: 프렌티스홀
• Alexei M. Tsvelik (2007). Quantum Field Theory in Condensed Matter Physics (2nd ed.). Cambridge University Press. ISBN 978-0-521-52980-8.
• A. N. Vasil'ev 임계 행동 이론 및 확률론적 역학에서의 현장 이론 재기명화 그룹 (Routregage Chapman & Hall 2004) ISBN 0-415-31002-4; ISBN 978-0-415-31002-4
• John E. Inglesfield (2015). The Embedding Method for Electronic Structure. IOP Publishing. ISBN 978-0-7503-1042-0.