강력한 회귀 분석 및 특이치 탐지

Robust Regression and Outlier Detection

강력한 회귀 분석 및 특이치 탐지는 강력한 통계에 대한 책으로, 특히 강력한 회귀 분석을 위한 방법의 분석 지점에 초점을 맞추고 있다.그것은 피터 루슈와 애닉 M에 의해 쓰여졌다.Leroy, 1987년에 Wiley에 의해 출판되었다.

배경

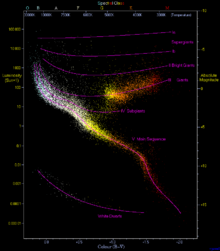
헤르츠스프룽-러셀 도표. 점성과 색상으로 표시된 별들.강력한 회귀 분석 방법은 주계열성에서 멀리 떨어진 항성 그룹의 영향을 받지 않고 이 도표의 중심곡선인 주계열성에 곡선을 적합시킬 수 있다.

선형 회귀 분석은 노이즈에 의해 관계가 가려진 데이터 집합에서 종속 변수와 하나 이상의 독립 변수 사이의 선형 함수 관계를 유추하는 문제다.일반 최소 제곱은 데이터가 모두 적합선 또는 평면 근처에 있다고 가정하지만 정규 분포 잔차 값을 추가하여 적합선으로부터 벗어난다.대조적으로, 강력한 회귀 방법은 일부 데이터 지점이 적합선이나 평면에 관계없는 특이치인 경우에도, 데이터가 출처의 혼합물에서 추출되기 때문일 수도 있고, 적대적 매개체가 회귀 방법을 부정확한 결과를 생성하기 위해 데이터를 손상시키려 하기 때문일 수도 있다.[1]이 책에서 논의된 전형적인 적용은 항성형식의 헤르츠스프룽-러셀 도표를 포함하고 있는데, 이 도표는 외딴 거성과 백색 왜성에 의해 던져지는 적합성 없이 항성의 주요 순서를 통해 곡선을 맞추기를 원하는 것이다.[2]강력한 회귀 분석 방법의 분석점은 정확성을 유지하면서 허용할 수 있는 외부 데이터의 비율이다.이러한 분석 스타일을 위해서는 더 높은 분석 점수가 더 좋다.[1]일반 최소 제곱의 분해점은 0에 가깝지만(단일 특이치가 있으면 적합치가 나머지 손상되지 않은 데이터에서 임의로 멀어질 수 있음)[2] 다른 방법에는 분해점이 50%[1]까지 높다.이러한 방법에는 데이터에 대한 가정이 거의 필요하지 않으며, 잡음이 잘 이해되지 않는 데이터에 대해서는 잘 작동하지만, 일반적인 최소 제곱보다 효율성이 다소 낮을 수 있으며(일정한 적합성 정확도를 위해 더 많은 데이터를 필요로 함) 구현이 복잡하고 느릴 수 있다.[3]

주제

그 책은 7장으로 되어 있다.[1][4]첫 번째는 도입이다. 간단한 선형 회귀(독립 변수가 하나밖에 없는 경우)를 설명하고, 종속변수나 독립변수를 손상시키는 특이치의 가능성을 논의하며, 특이치가 잘못된 결과를 생성하는 예를 제시하고, 분석점을 정의하며, 몇 가지 방법을 간략히 소개한다.반복된 중위수 회귀 분석을 포함한 강력한 단순 회귀 분석의 [1][2]경우두 번째 장과 세 번째 장은 회귀 분석의 최소 중위수 방법(잔차 제곱의 중위수를 최소화하는 적합치를 추구하는 방법)과 가장 잘린 제곱법(중위값 아래에 있는 제곱 잔차의 합을 최소화하는 방법)을 자세히 분석한다.이 두 가지 방법은 모두 분해점 50%를 가지며 단순 회귀 분석(2장)과 다변량 회귀 분석(3장) 모두에 적용할 수 있다.[1][5]최소 중위수는 (데이터의 절반을 포함하는 최소 높이의 스트립을 찾을 때) 매력적인 기하학적 설명을 가지고 있지만, 그 낮은 효율성으로 인해 최소 절삭 정사각형을 대신 사용할 것을 권고한다. 또한 최소 절삭 정사각형은 특이치를 찾고 제거하기 위해 최소 중위수 방법을 사용한 것으로 해석할 수 있다.나머지 데이터에 대한 단순 회귀 분석 [4]및 효율성의 단순 회귀 분석 접근.[6]이 장들은 이러한 방법들을 설명하고 그들의 통계적 속성을 분석하는 것뿐만 아니라, 이러한 방법들을 구현하기 위해 저자의 소프트웨어를 사용하는 방법도 설명한다.[1]세 번째 장에는 높은 고장점을 갖는 일부 대안 추정기에 대한 설명도 포함되어 있다.[7]

제4장에서는 위치 매개변수 또는 중심 경향의 1차원 추정과 그 소프트웨어 구현에 대해 설명하고, 제5장에서는 소프트웨어가 이러한 추정치를 효율적으로 계산하기 위해 사용하는 알고리즘에 대해 자세히 설명한다.여섯 번째 장은 다른 널리 사용되는 방법들과 견실한 통계에 기초하여 데이터 포인트를 특이치로서 식별하는 방법을 비교하면서 특이치 검출에 관한 것이며, 마지막 장은 타원체 또는 공분산 행렬을 데이터에 적합시키는 문제와 시계열 분석뿐만 아니라 고차원 위치 문제에 관한 것이다.[1][4][5][7]이 책은 통계적 방법을 비교하기 위해 분해점을 사용하는 것뿐만 아니라 그들의 모순도 살펴본다: 변환된 데이터에 대한 적합성이 원래 데이터에 대한 적합성의 변환 버전과 동일한가?[6]

이 책이 응용에 초점을 맞춘 것과 마찬가지로, 강력한 방법을 사용하여 수행된 분석의 많은 예를 특징으로 하며, 결과 추정치와 표준 비-로봇 방법을 통해 얻은 추정치를 비교한다.[3][7]이론 자료가 포함되지만 이론적으로 덜 삽입된 독자들이 쉽게 건너뛸 수 있도록 따로 둔다.저자들은 (두 방법의 결과가 일치하는 경우) 일반적인 회귀 분석의 적용 가능성을 확인하는 동시에 결과가 일치하지 않는 경우 이를 대체할 수 있는 강력한 방법을 사용할 수 있다는 입장을 취한다.[5]

청중 및 접대

이 책은 응용 통계학자들을 대상으로 하며, 이 책이 기술하는 강력한 방법을 사용하도록 설득하는 것을 목표로 하고 있다.[1]강력한 통계에서의 이전 연구와 달리, 그것은 실무자들이 사용할 수 있는 강력한 방법을 (관련 소프트웨어를 통해) 이해할 수 있게 한다.[3]기초 통계 기법의 일부 배경을 가정하더라도 강력한 통계에 대한 사전 지식이 필요하지 않다.[4][5]리뷰어 P. J. 레이콕이 그러한 사용의 가능성을 "볼트적이고 진보적"[4]이라고 부르고 리뷰어 시헐트와 그린은 그러한 과정이 영국의 통계 커리큘럼에 들어맞을 것 같지 않다고 지적하지만,[5] 이 책은 또한 교과서로 사용될 수 있다.[6]

세흘트와 그린 리뷰어들은 책의 너무 많은 부분이 저자들의 소프트웨어에 대한 사용자 가이드 역할을 하고 있으며, 잘랐어야 했다고 불평한다.[6]그러나, 검토자 그레고리 F.파이펠은 "프레젠테이션이 매우 좋다"고 쓰고, 그는 이 책을 통계적 방법을 사용하는 모든 사용자에게 추천한다.[1]카렌 카파다르는 일부 자료의 재주문을 제안하면서도 이 책을 대학원생들을 위한 교재와 전문가들을 위한 참고자료로 적극 추천하고 있다.[5]그리고 검토자 A. C.앳킨슨은 이 책을 "흥미롭고 중요한 책"[8]이라고 간결하게 요약했다.

관련서적

강력한 회귀 분석과 특출한 탐지에 관한 이전 책들은 다음과 같은 여러 권이 있었다.[5][7]

  • D. M. Hawkins에 의한 특이사항 식별 (1980)
  • Peter J. Huber에 의한 통계량(1981)
  • W. J. J. 레이(1983)에 의한 강건성 및 준-로봇성 통계방법 소개
  • David C의 강력하고 탐구적인 데이터 분석 이해.호글린, 프레더릭 모스텔러, 존 투키(1983)
  • Hampel, Ronchetti, Rousseuw 및 Stahel의 강력한 통계량(1986)

이에 비해, Robust Regression(강력한 회귀 분석)과 특이치 검출(특이치 검출)은 강건성과 특이치 탐지를 모두 결합한다.[5]이론이 적고, 데이터와 소프트웨어에 더 집중하며, 건전성의 다른 척도보다 고장점에 더 집중한다.[7]또한 독립변수의 값을 벗어난 표본이 중심값을 갖는 표본보다 적합치에 더 큰 영향을 미칠 수 있는 현상인 "레버리지"의 중요성을 가장 먼저 강조한다.[8]

참조

  1. ^ a b c d e f g h i j Piepel, Gregory F. (May 1989), "Review of Robust Regression and Outlier Detection", Technometrics, 31 (2): 260–261, doi:10.2307/1268828, JSTOR 1268828
  2. ^ a b c Sonnberger, Harold (July–September 1989), "Review of Robust Regression and Outlier Detection", Journal of Applied Econometrics, 4 (3): 309–311, JSTOR 2096530
  3. ^ a b c Weisberg, Stanford (July–August 1989), "Review of Robust Regression and Outlier Detection", American Scientist, 77 (4): 402–403, JSTOR 27855903
  4. ^ a b c d e Laycock, P. J. (1989), "Review of Robust Regression and Outlier Detection", Journal of the Royal Statistical Society, Series D (The Statistician), 38 (2): 138, doi:10.2307/2348319, JSTOR 2348319
  5. ^ a b c d e f g h Kafadar, Karen (June 1989), "Review of Robust Regression and Outlier Detection", Journal of the American Statistical Association, 84 (406): 617–618, doi:10.2307/2289958, JSTOR 2289958
  6. ^ a b c d Seheult, A. H.; Green, P. J. (1989), "Review of Robust Regression and Outlier Detection", Journal of the Royal Statistical Society, Series A (Statistics in Society), 152 (1): 133–134, doi:10.2307/2982847, JSTOR 2982847
  7. ^ a b c d e Yohai, V. J. (1989), "Review of Robust Regression and Outlier Detection", Mathematical Reviews and zbMATH, MR 0914792, Zbl 0711.62030
  8. ^ a b Atkinson, A. C. (June 1988), "Review of Robust Statistics and Robust Regression and Outlier Detection", Biometrics, 44 (2): 626–627, doi:10.2307/2531877, JSTOR 2531877