최단 경로 문제

가중치 유향 그래프에서 정점 A와 F 사이의 최단 경로(A, C, E, D, F)

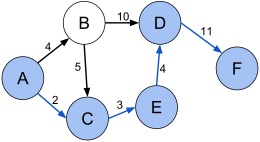
그래프 이론에서, 최단 경로 문제는 그래프에서 두 꼭지점(또는 노드) 사이의 경로를 찾는 문제이며, 구성 모서리의 가중치의 합이 최소화되도록 한다.

도로 지도에서 두 교차로 사이의 최단 경로를 찾는 문제는 그래프에서 최단 경로 문제의 특수한 경우로 모델링할 수 있다. 여기서 정점은 교차로에 대응하고 가장자리는 도로 세그먼트에 대응하며, 각각 세그먼트의 길이에 따라 가중치가 부여된다.

정의.

최단 경로 문제는 무방향, 방향 또는 혼합 그래프에 대해 정의할 수 있습니다.여기서 정의되는 것은 무방향 그래프의 경우입니다.유향 그래프의 경우 경로 정의를 위해서는 연속된 정점이 적절한 방향 가장자리에 의해 연결되어야 합니다.

두 정점은 둘 다 공통 모서리에 입사할 때 인접합니다.vertices P의 한 지도자 없는 그래프의 길은 시퀀스)(v1, v2,…,v n)∈ V×V× ⋯×V{\displaystyle P=(v_{1},v_{2},\ldots ,v_{n})\in V\times V\times \cdots V\times}가 vi{\displaystyle v_{나는}}은 산간 지대 v 나는 + 1{\displaystyle v_{i+1}}1≤ 나는 <, n{\displaystyle 1\le.q I<, n}. 그러한 경로 P{P\displaystyle}길이 n의 1{\displaystyle n-1}− v1{\displaystyle v_{1}에서 경로}n{\displaystyle v_{n}v에}라고 불린다.(나는{\displaystyle v_{나는}은 v}변수입니다;그들의 번호를 여기는 순서에서 그들의 위치며 어떤 c에 관련될 필요가 없게 서술하고 있ano꼭지점 라벨링)

$e_{i,j}$ i $e_{i,j}$ $(\$ 를 $e_{i,j}$ vi $(\$ }) 및 $v_{i}$ $v_{j}$ j $(\$ 의 에지 인시던트로 $e_{i,j}$ .실제 값 $f:E\rightarrow \mathbb {R}$ 함수 f $f:E\rightarrow \mathbb {R}$ $f:E\rightarrow \mathbb {R}$ $f:E\rightarrow \mathbb {R}$ $(\$ f $:$ $E\rightarrow \mathbb {R}$ 및 무방향(무방향) $그래프$ G({ $display$ G $G$ v({ $displaystyle$ v})에서 $v$ v $({$ v $')$ 까지의 $v'$ 최단 경로는 $P=(v_{1},v_{2},\ldots ,v_{n})$ $=$ ( $P=(v_{1},v_{2},\ldots ,v_{n})$ $,$ $P=(v_{1},v_{2},\ldots ,v_{n})$ $},$ \ $displaystyle$ P=( $v_1},$ { $2},$ { $n})입니다.$ $v_{n}=v'$ = $v$ { $v_{n}=v'$ $displaystyle$ v _ { $n }$ = $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ ' $v_{n}=v'$ ). n { displaystyle n $n$ }의 $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ 합계를 $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ 합니다 $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ ( ${ displaystyle$ \ $sum _ {i$ $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ }^{ $n-1}f(e_{i,i+$ 1}). $}$ 그래프의 $\sum _{i=1}^{n-1}f(e_{i,i+1}).$ 각 모서리에 단위 $f:E\rightarrow \{1\}$ 가 있거나 $f:E\rightarrow \{1\}$ : $f:E\rightarrow \{1\}$ { 1 $}$ {\ $displaystyle$ f: $E\rightarrow$ \{ $1$ 이것은 가장 엣지가 적은 경로를 찾는 것과 같습니다.

이 문제는 싱글 페어 최단 경로 문제라고도 불리며, 다음과 같은 차이와 구별됩니다.

단일 소스 최단 경로 문제: 소스 정점 v에서 그래프 내의 다른 모든 정점까지의 최단 경로를 찾아야 합니다.
단일 행선지 최단 패스 문제.유향 그래프의 모든 정점에서 단일 행선지 정점 v까지의 최단 패스를 찾아야 합니다.이것은 방향 그래프의 호를 반전시킴으로써 단일 소스 최단 경로 문제로 줄일 수 있습니다.
전체 쌍 최단 경로 문제. 그래프에서 모든 정점 쌍 v, v' 사이의 최단 경로를 찾아야 합니다.

이러한 일반화는 관련된 모든 정점 쌍에서 단일 쌍 최단 경로 알고리즘을 실행하는 단순한 접근 방식보다 훨씬 효율적인 알고리즘을 가지고 있습니다.

알고리즘

이 문제를 해결하기 위한 가장 중요한 알고리즘은 다음과 같습니다.

Dijkstra의 알고리즘은 음이 아닌 에지 웨이트로 단일 소스 최단 경로 문제를 해결합니다.
Bellman-Ford 알고리즘은 엣지 무게가 음수인 경우 단일 소스 문제를 해결합니다.
A* 검색 알고리즘은 검색 속도를 높이기 위해 휴리스틱스를 사용하여 단일 쌍 최단 경로를 해결합니다.
Floyd-Warshall 알고리즘은 모든 쌍의 최단 경로를 해결합니다.
Johnson의 알고리즘은 모든 최단 경로 쌍을 해결하며, 희박한 그래프에서 Floyd-Warshall보다 더 빠를 수 있다.
Viterbi 알고리즘은 각 노드에서 추가 확률적 가중치로 최단 확률 경로 문제를 해결한다.

추가 알고리즘 및 관련 평가는 Cherkassky, Goldberg & Radzik(1996)에서 확인할 수 있다.

단일 소스 최단 경로

무방향 그래프

중량	시간의 복잡성	작가.
$\displaystyle \mathbb {R}$ ₊	O(V²)	다이크스트라 1959
$\displaystyle \mathbb {R}$ ₊	O((E + V) 로그 V)	존슨 1977(이진 힙)
$\displaystyle \mathbb {R}$ ₊	O(E + V 로그 V)	Fredman & Tarjan 1984 (Fibonacci 힙)
$\displaystyle \mathbb {N}$	O(E)	Thorup 1999(정시 곱셈 필요)

가중치 없는 그래프

알고리즘.	시간의 복잡성	작가.
폭 우선 검색	O(E+V)

유도 비순환 그래프(DAG)

위상 정렬을 사용하는 알고리즘은 임의 가중 DAG에서 시간 ^[1] $δ(E$ + $V)$ 내의 단일 소스 최단 경로 문제를 해결할 수 있다.

음수가 아닌 가중치를 갖는 유도 그래프

다음 표는 Schrijver(2004)에서 일부 수정 및 추가 내용을 인용한 것이다.녹색 배경은 테이블에서 점근적으로 가장 적합한 경계를 나타냅니다. L은 정수 에지 가중치를 가정한 모든 에지 중 최대 길이(또는 가중치)입니다.

중량	알고리즘.	시간의 복잡성	작가.
$\displaystyle \mathbb {R}$		$O(V^{2}EL)$	포드 1956
$\displaystyle \mathbb {R}$	벨먼-포드 알고리즘	$O(VE)$	심벨 1955, 벨만 1958, 무어 1959
$\displaystyle \mathbb {R}$		$O(V^{2}\log {V}}$	단치히 1960
$\displaystyle \mathbb {R}$	리스트가 있는 다이크스트라의 알고리즘	$O(V^{2})$	Leyzorek et al. 1957, Dijkstra 1959, Minty(Polock & Wiebenson 1960 참조), Whiting & Hillier 1960
$\displaystyle \mathbb {R}$	이진 힙을 사용하는 Dijkstra 알고리즘	$O((E+V)\log {V})$	존슨 1977
$\displaystyle \mathbb {R}$	Dijkstra의 피보나치 힙 알고리즘	$O(E+V\log {V})$	Fredman & Tarjan 1984, Fredman & Tarjan 1987
$\displaystyle \mathbb {N}$	다이얼 알고리즘^[2](L 버킷이 있는 버킷큐를 사용하는 Dijkstra 알고리즘)	$O(E+LV)$	다이얼 1969
		$({displaystyle O(E\log {L}})})$	존슨 1981, 칼슨 & 포블레 1983
	가보우 알고리즘	$O(E\log_{E/V}L)$	Gabow 1983, Gabow 1985
		$(\displaystyle O(E+V{\sqrt {L}})}$	아후자 외 1990년
	토루프	$({displaystyle O(E+V\log {V}})})$	토룹 2004

음수 주기가 없는 임의의 가중치를 가진 유도 그래프

중량	알고리즘.	시간의 복잡성	작가.
$\displaystyle \mathbb {R}$		O(벨²)	포드 1956
$\displaystyle \mathbb {R}$	벨먼-포드 알고리즘	O(VE)	심벨 1955, 벨만 1958, 무어 1959
$\displaystyle \mathbb {R}$	Johnson-Dijkstra(바이너리 힙 포함)	O(V)(E + 로그 V)	존슨 1977
$\displaystyle \mathbb {R}$	Johnson-Dijkstra with Fibonacci 힙	O(V)(E + 로그 V)	Fredman & Tarjan 1984, Fredman & Tarjan 1987, Johnson 1977 이후 개작
$\displaystyle \mathbb {N}$	다이얼 알고리즘에^[2] 적용되는 존슨 기술	O(V) (E + L)	1969년 다이얼, 1977년 존슨 이후 개작

음수 주기의 임의 가중치를 갖는 유도 그래프

음수 주기를 찾거나 모든 정점까지의 거리를 계산합니다.

중량	알고리즘.	시간의 복잡성	작가.
$\displaystyle \mathbb {Z}$	앤드류 V. 골드버그	$O(E{\sqrt {V}}}\log {N})$

임의의 가중치를 갖는 평면 방향 그래프

모두 쌍으로 구성된 최단 경로

모두 쌍으로 구성된 최단 경로 문제는 그래프에서 $모든$ 정점 쌍 $v,$ v' 사이의 최단 경로를 찾습니다.무가중 유도 그래프에 대한 전체 쌍 최단 경로 문제는 총 O $(V 4)$ $시간$ 이 걸리는 선형 행렬 곱셈으로 해결할 수 있다고 관찰한 Shimbel(1953)에 의해 도입되었다.

무방향 그래프

중량	시간의 복잡성	알고리즘.
$\displaystyle \mathbb {R}$ ₊	$O (V 3)$	플로이드-워셜 알고리즘
$(\displaystyle\{1,\infty\})$	$O(V^{\omega}\log V}$	세이델 알고리즘(예상 실행 시간)
$\displaystyle \mathbb {N}$	$(\displaystyle O(V^{3}/2^{\Omega (\log n)^{1/2}})})$	윌리엄스 2014
$\displaystyle \mathbb {R}$ ₊	$O (EV 로그α(E, V))$	Pettie & Ramachandran 2002
$\displaystyle \mathbb {N}$	$O (EV)$	Torup 1999는 모든 정점에 적용됩니다(정시 곱셈 필요).

유향 그래프

중량	시간의 복잡성	알고리즘.
$\mathbb {R}$ \ $displaystyle \mathbb {R}$ (부정 사이클 없음)	$O (V 3)$	플로이드-워셜 알고리즘
$\displaystyle \mathbb {N}$	$(\displaystyle O(V^{3}/2^{\Omega (\log n)^{1/2}})})$	윌리엄스 2014
$\mathbb {R}$ \ $displaystyle \mathbb {R}$ (부정 사이클 없음)	$O (EV + V 2 로그 V)$	존슨-다이크스트라
$\mathbb {R}$ \ $displaystyle \mathbb {R}$ (부정 사이클 없음)	$O (EV + V 2 로그 로그 V)$	페티 2004
$\displaystyle \mathbb {N}$	$O (EV + V 2 로그 로그 V)$	헤이거업 2000

적용들

최단 경로 알고리즘은 MapQuest 또는 Google Maps와 같은 웹 지도 웹 사이트에서 주행 경로와 같이 물리적 위치 간의 방향을 자동으로 찾기 위해 적용됩니다.이 애플리케이션에는 고속 특수 알고리즘을 사용할 ^[3]수 있습니다.

정점이 상태를 기술하고 가장자리가 가능한 전이를 기술하는 그래프로 비결정론적 추상기계를 나타낼 경우, 최단 경로 알고리즘은 특정 목표 상태에 도달하기 위한 최적의 선택 시퀀스를 찾거나 특정 상태에 도달하는 데 필요한 시간의 하한을 설정하기 위해 사용될 수 있다.예를 들어, 정점이 루빅스 큐브와 같은 퍼즐의 상태를 나타내며 각 방향 가장자리가 한 번의 이동 또는 회전에 해당하는 경우, 최단 경로 알고리즘을 사용하여 가능한 최소 이동 수를 사용하는 솔루션을 찾을 수 있습니다.

네트워킹 또는 통신 사고방식에서는 이 최단 경로 문제를 최소 지연 경로 문제라고 부르기도 하며, 일반적으로 가장 넓은 경로 문제와 관련이 있습니다.예를 들어 알고리즘은 최단(min-delay)의 가장 넓은 경로 또는 가장 넓은(min-delay) 경로를 찾을 수 있습니다.

더 가벼운 응용 프로그램은 같은 영화에 나오는 영화배우처럼 그래프에서 최단 경로를 찾는 "6단계 분리" 게임이다.

운영 연구에서 종종 연구되는 다른 애플리케이션으로는 플랜트 및 설비 레이아웃, 로봇 설계,^[4] 운송 및 VLSI 설계가 있습니다.

도로망

도로 네트워크는 양의 가중치를 갖는 그래프로 간주할 수 있습니다.노드는 도로 교차로를 나타내며 그래프의 각 가장자리는 두 교차로 사이의 도로 세그먼트와 연결됩니다.모서리의 무게는 연결된 도로 세그먼트의 길이, 세그먼트를 통과하는 데 필요한 시간 또는 세그먼트를 통과하는 비용과 일치할 수 있습니다.방향 가장자리를 사용하여 편도 거리를 모델링할 수도 있습니다.이러한 그래프는 장거리 이동(예: 고속도로)에서 일부 모서리가 다른 모서리보다 더 중요하다는 점에서 특별하다.이 속성은 고속도로 ^[5]치수 개념을 사용하여 공식화되었습니다.이 속성을 이용하여 일반 그래프에서 가능한 것보다 훨씬 빠르게 최단 경로를 계산할 수 있는 알고리즘이 많이 있습니다.

이러한 알고리즘은 모두 2단계로 동작합니다.첫 번째 단계에서는 소스 노드 또는 타깃 노드를 인식하지 않고 그래프를 전처리한다.두 번째 단계는 쿼리 단계입니다.이 단계에서는 소스 노드와 타깃노드가 인식됩니다.즉, 도로 네트워크는 정적이므로 전처리 단계를 한 번 수행하여 동일한 도로 네트워크에서 다수의 쿼리에 사용할 수 있습니다.

가장 빠른 쿼리 시간을 가진 알고리즘은 허브 라벨링이라고 불리며, 유럽 또는 미국의 도로망에서 단 1 마이크로초 ^[6]만에 최단 경로를 계산할 수 있습니다.기타 사용된 기술은 다음과 같습니다.

ALT(A* 검색, 랜드마크 및 삼각 부등식)
호 플래그
수축 계층
중계 노드 라우팅
리치 베이스 플루닝
라벨링
허브 라벨

선형 프로그래밍 공식

최단 경로 문제에 대한 자연스러운 선형 프로그래밍 공식은 다음과 같습니다.이것은 이산 최적화에서 선형 프로그램을 사용하는 대부분의 다른 방법과 비교하면 매우 간단하지만, 다른 개념과의 연결을 보여줍니다.

소스 노드 s, 대상 노드 t 및 A의 각 에지(i, j)에 대한 비용_ij w가 포함된 방향 그래프(V, A)를 지정하면 변수가_ij x인 프로그램을 고려합니다.

\sum _{ij\in A}w_{ij}x_{ij}

i j

\sum _{ij\in A}w_{ij}x_{ij}

A

\sum _{ij\in A}w_{ij}x_{ij}

\sum _{ij\in A}w_{ij}x_{ij}

j

\sum _{ij\in A}w_{ij}x_{ij}

i

\sum _{ij\in A}w_{ij}x_{ij}

_ {

ij

\

in

A

}

w

\sum _{ij\in A}w_{ij}x_{ij}

_ {

ij

} w _ {

ij

} x _

\sum _{ij\in A}w_{ij}x_{ij}

{

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

} minimize x

_

{

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

ij

}

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

i의 경우,

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

j -

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

j

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

;

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

,

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

,

\sum _{j}x_{ij}-\sum _{j}x_{ji}={\begin{cases}1,&{\text{if }}i=s;\\-1,&{\text{if }}i=t;\\0,&{\text{ otherwise.}}\end{cases}}

、）。

\displaystyle \sum _{j}x_{ij}-\sum _{j}x_{ji}=case}1,&{\text{if}i=s;\-1,&{\text{if}i=t;\0,&{\text}

}}\end {case}}

이 배경에는 $x_{ij}$ j(\ $displaystyle x_{ij})$ 가 $x_{ij}$ 최단 경로의 일부인지 여부를 나타내는 인디케이터 $x_{ij}$ 라는 직감이 있습니다.즉, 엣지(i, j)가 최단 경로의 일부인지 아닌지는 1이고, 그렇지 않은 경우는 0개입니다.이 세트가 s에서 t까지의 경로를 형성한다는 제약조건에 따라 최소 무게의 에지 세트를 선택하고자 한다(등식 제약조건으로 표시됨: s와 t를 제외한 모든 정점에 대해 경로의 일부인 들어오는 에지 및 나가는 에지 수가 동일해야 한다(즉, s에서 t로의 경로가 되어야 함).

이 LP는 적분이라는 특수 특성을 가지고 있습니다. 보다 구체적으로, 모든 기본 최적 솔루션(존재하는 경우)은 0 또는 1과 같은 모든 변수를 가지며 변수가 1인 에지 집합은 s-t 이중 경로를 형성합니다.이 접근법의 기원은 ^[13]20세기 중반으로 거슬러 올라가지만 한 가지 증거는 Ahuja 등을 참조하십시오.

이 선형 프로그램의 듀얼은

모든 ij, y_j - y_i w_ij w에 대해 y - y를_s 최대화합니다_t.

및 피지블 듀얼은 최단 경로의 A* 알고리즘에 대한 일관된 휴리스틱 개념에 해당합니다.실현 가능한 모든 이중 y에 대해 $w'_{ij}=w_{ij}-y_{j}+y_{i}$ j $w'_{ij}=w_{ij}-y_{j}+y_{i}$ $=$ $w'_{ij}=w_{ij}-y_{j}+y_{i}$ $w'_{ij}=w_{ij}-y_{j}+y_{i}$ - $w'_{ij}=w_{ij}-y_{j}+y_{i}$ j + $w'_{ij}=w_{ij}-y_{j}+y_{i}$ $w'_{ij}=w_{ij}-y_{j}+y_{i}$ { $displaystyle$ w $'_{ij$ }= $w_{ij}-y_{j}+y_$ { $i$ }}는 $w'_{ij}=w_{ij}-y_{j}+y_{i}$ 음이 아니며, A*는 기본적으로 이러한 비용 절감에 대한 Dikstra의 알고리즘을 실행한다.

반고리에 관한 일반적인 대수적 프레임워크: 대수적 경로 문제

많은 문제들이 경로를 따라 추가되고 최소로 취한다는 적절히 대체된 개념에 대해 최단 경로의 형태로 프레임화될 수 있다.이에 대한 일반적인 접근법은 두 가지 연산을 세미닝 연산으로 간주하는 것입니다.세미닝 곱셈은 경로를 따라 수행되며, 추가는 경로 간에 수행됩니다.이 일반적인 틀은 대수 경로 ^[14]^[15]^[16]문제로 알려져 있다.

대부분의 고전적인 최단 경로 알고리즘(및 새로운 알고리즘)은 그러한 대수적 ^[17]구조에 대한 선형 시스템을 푸는 것으로 공식화할 수 있다.

보다 최근에는 이러한 문제(그리고 훨씬 덜 명백하게 관련된 문제)를 해결하기 위한 훨씬 더 일반적인 프레임워크가 평가 ^[18]대수의 기치 아래 개발되었다.

확률적 시간 의존 네트워크에서의 최단 경로

실제 상황에서, 교통 네트워크는 대개 확률적이고 시간에 의존합니다.실제로 매일 링크를 통과하는 여행자는 여행 수요의 변동(원점-목적지 매트릭스)뿐만 아니라 작업 구역, 악천후, 사고 및 차량 고장 등의 사고로 인해 해당 링크에서 다른 여행 시간을 경험할 수 있습니다.그 결과 확률적 시간 의존적(STD) 네트워크는 결정론적 ^[19]^[20]네트워크와 비교하여 실제 도로 네트워크의 보다 현실적인 표현이다.

지난 10년 동안 상당한 진전이 있었음에도 불구하고, 확률적 도로 네트워크에서 최적의 경로를 정의하고 식별해야 하는 방법은 여전히 논란의 여지가 있는 질문으로 남아 있다.다시 말해, 불확실성 하에서 최적의 경로에 대한 고유한 정의는 없다.이 질문에 대한 한 가지 가능한 일반적인 대답은 예상 이동 시간이 최소인 경로를 찾는 것입니다.이 접근방식을 사용하는 주된 장점은 결정론적 네트워크에 도입된 효율적인 최단 경로 알고리즘이 확률적 네트워크에서 최소 예상 이동 시간으로 경로를 식별하기 위해 쉽게 사용될 수 있다는 것이다.그러나, 이 접근법이 이동 시간 변동을 다루지 못하기 때문에, 이 접근법에 의해 식별된 최적의 경로는 신뢰할 수 없을 수 있다.이 문제를 해결하기 위해 일부 연구자들은 이동 시간의 분포를 예상 값 대신 사용합니다. 그래서 그들은 동적 프로그래밍과 Dijkstra의 [21]알고리즘과 같은 다른 최적화 방법을 사용하여 총 이동 시간의 확률 분포를 찾습니다.이러한 방법들은 확률론적 호 ^[22]길이를 가진 네트워크에서 최단 경로를 찾기 위해 확률적 최적화, 특히 확률적 동적 프로그래밍을 사용한다.이동시간 신뢰성의 개념은 교통 연구 문헌에서 이동시간 변동과 상호 호환되게 사용되므로 일반적으로 이동시간의 변동성이 높을수록 신뢰성이 낮아지고 그 반대도 마찬가지라고 말할 수 있다.

이동 시간 신뢰성을 보다 정확하게 설명하기 위해 불확실성 하에서의 최적 경로에 대한 두 가지 일반적인 대체 정의가 제시되었다.일부는 주어진 이동 시간 예산보다 제시간에 또는 일찍 도착할 확률을 극대화하는 것을 목표로 가장 신뢰할 수 있는 경로의 개념을 도입했습니다.다른 사람들은 사전 지정된 정시 도착 확률을 보장하기 위해 필요한 이동 시간 예산을 최소화하기 위해 α 신뢰 경로의 개념을 제시했다.

「」를 참조해 주세요.

양방향 검색, 방향 그래프에서 두 꼭지점 사이의 최단 경로를 찾는 알고리즘
유클리드 최단 경로
플로우 네트워크
K 최단 경로 라우팅
최소 행렬 곱셈
경로 검색
최단 패스 브리징
최단 경로 트리
TRIL(트랜스페어런트 링크 상호접속)

레퍼런스

메모들

^ Cormen 등 2001, 페이지 655 harvnb 오류: 대상 없음: CITREFCormenLeisersonRivestStein2001 (도움말)
^ ^a ^b Dial, Robert B. (1969). "Algorithm 360: Shortest-Path Forest with Topological Ordering [H]". Communications of the ACM. 12 (11): 632–633. doi:10.1145/363269.363610. S2CID 6754003.
^ Sanders, Peter (March 23, 2009). "Fast route planning". Google Tech Talk. Archived from the original on 2021-12-11.
^ Chen, Danny Z. (December 1996). "Developing algorithms and software for geometric path planning problems". ACM Computing Surveys. 28 (4es). Article 18. doi:10.1145/242224.242246. S2CID 11761485.
^ 아브라함, 잇타이, 피아트, 아모스, 골드버그, 앤드류 5세;Werneck, Renato F. "고속도로 치수, 최단 경로 및 입증 가능한 효율적인 알고리즘"이산 알고리즘에 관한 ACM-SIAM 심포지엄(782-793페이지), 2010.
^ 아브라함, 잇타이, 델링, 다니엘, 골드버그, 앤드류 5세;Werneck, Renato F. research.microsoft.com/pubs/142356/HL-TR.pdf "도로 네트워크의 최단 경로를 위한 허브 기반 라벨링 알고리즘"실험 알고리즘에 관한 심포지엄, 230–241페이지, 2011.
^ Kroger, Martin (2005). "Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems". Computer Physics Communications. 168 (3): 209–232. Bibcode:2005CoPhC.168..209K. doi:10.1016/j.cpc.2005.01.020.
^ Lozano, Leonardo; Medaglia, Andrés L (2013). "On an exact method for the constrained shortest path problem". Computers & Operations Research. 40 (1): 378--384. doi:10.1016/j.cor.2012.07.008.
^ Osanlou, Kevin; Bursuc, Andrei; Guettier, Christophe; Cazenave, Tristan; Jacopin, Eric (2019). "Optimal Solving of Constrained Path-Planning Problems with Graph Convolutional Networks and Optimized Tree Search". 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS): 3519--3525. arXiv:2108.01036. doi:10.1109/IROS40897.2019.8968113. ISBN 978-1-7281-4004-9. S2CID 210706773.
^ Bar-Noy, Amotz; Schieber, Baruch (1991). "The canadian traveller problem". Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms: 261–270. CiteSeerX 10.1.1.1088.3015.
^ Nikolova, Evdokia; Karger, David R. "Route planning under uncertainty: the Canadian traveller problem" (PDF). Proceedings of the 23rd National Conference on Artificial Intelligence (AAAI): 969--974.
^ Cherkassky, Boris V.; Goldberg, Andrew V. (1999-06-01). "Negative-cycle detection algorithms". Mathematical Programming. 85 (2): 277–311. doi:10.1007/s101070050058. ISSN 1436-4646.
^ Ahuja, Ravindra K.; Magnanti, Thomas L.; Orlin, James B. (1993). Network Flows: Theory, Algorithms and Applications. Prentice Hall. ISBN 978-0-13-617549-0.
^ Pair, Claude (1967). "Sur des algorithmes pour des problèmes de cheminement dans les graphes finis (On algorithms for path problems in finite graphs)". In Rosentiehl, Pierre (ed.). Théorie des graphes (journées internationales d'études) -- Theory of Graphs (international symposium). Rome (Italy), July 1966: Dunod (Paris) et Gordon and Breach (New York). p. 271.{{cite conference}}: CS1 유지보수: 위치(링크)
^ Derniame, Jean Claude; Pair, Claude (1971). Problèmes de cheminement dans les graphes (Path Problems in Graphs). Dunod (Paris).
^ Baras, John; Theodorakopoulos, George (4 April 2010). Path Problems in Networks. Morgan & Claypool Publishers. pp. 9–. ISBN 978-1-59829-924-3.
^ Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Springer Science & Business Media. chapter 4. ISBN 978-0-387-75450-5.
^ Pouly, Marc; Kohlas, Jürg (2011). Generic Inference: A Unifying Theory for Automated Reasoning. John Wiley & Sons. Chapter 6. Valuation Algebras for Path Problems. ISBN 978-1-118-01086-0.
^ 루이, R.P., 1983년확률적 또는 다차원 가중치를 가진 그래프에서 최적의 경로입니다.ACM의 통신, 26(9) 페이지 670-676.
^ Rajabi-Bahaabadi, Mojtaba; Shariat-Mohaymany, Afshin; Babaei, Mohsen; Ahn, Chang Wook (2015). "Multi-objective path finding in stochastic time-dependent road networks using non-dominated sorting genetic algorithm". Expert Systems with Applications. 42 (12): 5056–5064. doi:10.1016/j.eswa.2015.02.046.
^ Olya, Mohammad Hessam (2014). "Finding shortest path in a combined exponential – gamma probability distribution arc length". International Journal of Operational Research. 21 (1): 25–37. doi:10.1504/IJOR.2014.064020.
^ Olya, Mohammad Hessam (2014). "Applying Dijkstra's algorithm for general shortest path problem with normal probability distribution arc length". International Journal of Operational Research. 21 (2): 143–154. doi:10.1504/IJOR.2014.064541.

참고 문헌

Ahuja, Ravindra K.; Mehlhorn, Kurt; Orlin, James; Tarjan, Robert E. (April 1990). "Faster algorithms for the shortest path problem" (PDF). Journal of the ACM. ACM. 37 (2): 213–223. doi:10.1145/77600.77615. hdl:1721.1/47994. S2CID 5499589.
Bellman, Richard (1958). "On a routing problem". Quarterly of Applied Mathematics. 16: 87–90. doi:10.1090/qam/102435. MR 0102435.
Cherkassky, Boris V.; Goldberg, Andrew V.; Radzik, Tomasz (1996). "Shortest paths algorithms: theory and experimental evaluation". Mathematical Programming. Ser. A. 73 (2): 129–174. doi:10.1016/0025-5610(95)00021-6. MR 1392160.
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Single-Source Shortest Paths and All-Pairs Shortest Paths". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 580–642. ISBN 0-262-03293-7.
Dantzig, G. B. (January 1960). "On the Shortest Route through a Network". Management Science. 6 (2): 187–190. doi:10.1287/mnsc.6.2.187.
Dijkstra, E. W. (1959). "A note on two problems in connexion with graphs". Numerische Mathematik. 1: 269–271. doi:10.1007/BF01386390. S2CID 123284777.
Ford, L. R. (1956). "Network Flow Theory". Rand Corporation. P-923. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
Fredman, Michael Lawrence; Tarjan, Robert E. (1984). Fibonacci heaps and their uses in improved network optimization algorithms. 25th Annual Symposium on Foundations of Computer Science. IEEE. pp. 338–346. doi:10.1109/SFCS.1984.715934. ISBN 0-8186-0591-X.
Fredman, Michael Lawrence; Tarjan, Robert E. (1987). "Fibonacci heaps and their uses in improved network optimization algorithms". Journal of the Association for Computing Machinery. 34 (3): 596–615. doi:10.1145/28869.28874. S2CID 7904683.
Gabow, H. N. (1983). "Scaling algorithms for network problems". Proceedings of the 24th Annual Symposium on Foundations of Computer Science (FOCS 1983) (PDF). pp. 248–258. doi:10.1109/SFCS.1983.68.
Gabow, Harold N. (1985). "Scaling algorithms for network problems". Journal of Computer and System Sciences. 31 (2): 148–168. doi:10.1016/0022-0000(85)90039-X. MR 0828519.
Hagerup, Torben (2000). Montanari, Ugo; Rolim, José D. P.; Welzl, Emo (eds.). Improved Shortest Paths on the Word RAM. Proceedings of the 27th International Colloquium on Automata, Languages and Programming. pp. 61–72. ISBN 978-3-540-67715-4.
Johnson, Donald B. (1977). "Efficient algorithms for shortest paths in sparse networks". Journal of the ACM. 24 (1): 1–13. doi:10.1145/321992.321993. S2CID 207678246.
Altıntaş, Gökhan (2020). Exact Solutions of Shortest-Path Problems Based on Mechanical Analogies: In Connection with Labyrinths. Amazon Digital Services LLC. p. 97. ISBN 9798655831896.
Johnson, Donald B. (December 1981). "A priority queue in which initialization and queue operations take $O (log log D)$ time". Mathematical Systems Theory. 15 (1): 295–309. doi:10.1007/BF01786986. MR 0683047. S2CID 35703411.
Karlsson, Rolf G.; Poblete, Patricio V. (1983). "An $O (m log log D)$ algorithm for shortest paths". Discrete Applied Mathematics. 6 (1): 91–93. doi:10.1016/0166-218X(83)90104-X. MR 0700028.
Leyzorek, M.; Gray, R. S.; Johnson, A. A.; Ladew, W. C.; Meaker, S. R., Jr.; Petry, R. M.; Seitz, R. N. (1957). Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems. Cleveland, Ohio: Case Institute of Technology.
Moore, E. F. (1959). "The shortest path through a maze". Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957). Cambridge: Harvard University Press. pp. 285–292.
Pettie, Seth; Ramachandran, Vijaya (2002). Computing shortest paths with comparisons and additions. Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms. pp. 267–276. ISBN 978-0-89871-513-2.
Pettie, Seth (26 January 2004). "A new approach to all-pairs shortest paths on real-weighted graphs". Theoretical Computer Science. 312 (1): 47–74. doi:10.1016/s0304-3975(03)00402-x.
Pollack, Maurice; Wiebenson, Walter (March–April 1960). "Solution of the Shortest-Route Problem—A Review". Oper. Res. 8 (2): 224–230. doi:10.1287/opre.8.2.224. 225페이지의 Dijkstra의 알고리즘을 Minty("개인 통신")에 귀속시킵니다.
Schrijver, Alexander (2004). Combinatorial Optimization — Polyhedra and Efficiency. Algorithms and Combinatorics. Vol. 24. Springer. ISBN 978-3-540-20456-5. 여기: volume.A, 7.5b장, 페이지 103
Shimbel, Alfonso (1953). "Structural parameters of communication networks". Bulletin of Mathematical Biophysics. 15 (4): 501–507. doi:10.1007/BF02476438.
Shimbel, A. (1955). Structure in communication nets. Proceedings of the Symposium on Information Networks. New York, NY: Polytechnic Press of the Polytechnic Institute of Brooklyn. pp. 199–203.
Thorup, Mikkel (1999). "Undirected single-source shortest paths with positive integer weights in linear time". Journal of the ACM. 46 (3): 362–394. doi:10.1145/316542.316548. S2CID 207654795.
Thorup, Mikkel (2004). "Integer priority queues with decrease key in constant time and the single source shortest paths problem". Journal of Computer and System Sciences. 69 (3): 330–353. doi:10.1016/j.jcss.2004.04.003.
Whiting, P. D.; Hillier, J. A. (March–June 1960). "A Method for Finding the Shortest Route through a Road Network". Operational Research Quarterly. 11 (1/2): 37–40. doi:10.1057/jors.1960.32.
Williams, Ryan (2014). "Faster all-pairs shortest paths via circuit complexity". Proceedings of the 46th Annual ACM Symposium on Theory of Computing (STOC '14). New York: ACM. pp. 664–673. arXiv:1312.6680. doi:10.1145/2591796.2591811. MR 3238994.

추가 정보

Frigioni, D.; Marchetti-Spaccamela, A.; Nanni, U. (1998). "Fully dynamic output bounded single source shortest path problem". Proc. 7th Annu. ACM-SIAM Symp. Discrete Algorithms. Atlanta, GA. pp. 212–221. CiteSeerX 10.1.1.32.9856.
Dreyfus, S. E. (October 1967). An Appraisal of Some Shortest Path Algorithms (PDF) (Report). Project Rand. United States Air Force. RM-5433-PR. Archived (PDF) from the original on November 17, 2015. DTIC AD-661265

[1] Cormen 등 2001, 페이지 655 harvnb 오류: 대상 없음: CITREFCormenLeisersonRivestStein2001 (도움말)

[dial69-2] Dial, Robert B. (1969). "Algorithm 360: Shortest-Path Forest with Topological Ordering [H]". Communications of the ACM. 12 (11): 632–633. doi:10.1145/363269.363610. S2CID 6754003.

[3] Sanders, Peter (March 23, 2009). "Fast route planning". Google Tech Talk. Archived from the original on 2021-12-11.

[4] Chen, Danny Z. (December 1996). "Developing algorithms and software for geometric path planning problems". ACM Computing Surveys. 28 (4es). Article 18. doi:10.1145/242224.242246. S2CID 11761485.

[5] 아브라함, 잇타이, 피아트, 아모스, 골드버그, 앤드류 5세;Werneck, Renato F. "고속도로 치수, 최단 경로 및 입증 가능한 효율적인 알고리즘"이산 알고리즘에 관한 ACM-SIAM 심포지엄(782-793페이지), 2010.

[6] 아브라함, 잇타이, 델링, 다니엘, 골드버그, 앤드류 5세;Werneck, Renato F. research.microsoft.com/pubs/142356/HL-TR.pdf "도로 네트워크의 최단 경로를 위한 허브 기반 라벨링 알고리즘"실험 알고리즘에 관한 심포지엄, 230–241페이지, 2011.

[7] Kroger, Martin (2005). "Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems". Computer Physics Communications. 168 (3): 209–232. Bibcode:2005CoPhC.168..209K. doi:10.1016/j.cpc.2005.01.020.

[8] Lozano, Leonardo; Medaglia, Andrés L (2013). "On an exact method for the constrained shortest path problem". Computers & Operations Research. 40 (1): 378--384. doi:10.1016/j.cor.2012.07.008.

[9] Osanlou, Kevin; Bursuc, Andrei; Guettier, Christophe; Cazenave, Tristan; Jacopin, Eric (2019). "Optimal Solving of Constrained Path-Planning Problems with Graph Convolutional Networks and Optimized Tree Search". 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS): 3519--3525. arXiv:2108.01036. doi:10.1109/IROS40897.2019.8968113. ISBN 978-1-7281-4004-9. S2CID 210706773.

[10] Bar-Noy, Amotz; Schieber, Baruch (1991). "The canadian traveller problem". Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms: 261–270. CiteSeerX 10.1.1.1088.3015.

[11] Nikolova, Evdokia; Karger, David R. "Route planning under uncertainty: the Canadian traveller problem" (PDF). Proceedings of the 23rd National Conference on Artificial Intelligence (AAAI): 969--974.

[12] Cherkassky, Boris V.; Goldberg, Andrew V. (1999-06-01). "Negative-cycle detection algorithms". Mathematical Programming. 85 (2): 277–311. doi:10.1007/s101070050058. ISSN 1436-4646.

[13] Ahuja, Ravindra K.; Magnanti, Thomas L.; Orlin, James B. (1993). Network Flows: Theory, Algorithms and Applications. Prentice Hall. ISBN 978-0-13-617549-0.

[Pair1966-14] Pair, Claude (1967). "Sur des algorithmes pour des problèmes de cheminement dans les graphes finis (On algorithms for path problems in finite graphs)". In Rosentiehl, Pierre (ed.). Théorie des graphes (journées internationales d'études) -- Theory of Graphs (international symposium). Rome (Italy), July 1966: Dunod (Paris) et Gordon and Breach (New York). p. 271.{{cite conference}}: CS1 유지보수: 위치(링크)

[15] Derniame, Jean Claude; Pair, Claude (1971). Problèmes de cheminement dans les graphes (Path Problems in Graphs). Dunod (Paris).

[BarasTheodorakopoulos2010-16] Baras, John; Theodorakopoulos, George (4 April 2010). Path Problems in Networks. Morgan & Claypool Publishers. pp. 9–. ISBN 978-1-59829-924-3.

[GondranMinoux2008-17] Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Springer Science & Business Media. chapter 4. ISBN 978-0-387-75450-5.

[PoulyKohlas2012-18] Pouly, Marc; Kohlas, Jürg (2011). Generic Inference: A Unifying Theory for Automated Reasoning. John Wiley & Sons. Chapter 6. Valuation Algebras for Path Problems. ISBN 978-1-118-01086-0.

[19] 루이, R.P., 1983년확률적 또는 다차원 가중치를 가진 그래프에서 최적의 경로입니다.ACM의 통신, 26(9) 페이지 670-676.

[20] Rajabi-Bahaabadi, Mojtaba; Shariat-Mohaymany, Afshin; Babaei, Mohsen; Ahn, Chang Wook (2015). "Multi-objective path finding in stochastic time-dependent road networks using non-dominated sorting genetic algorithm". Expert Systems with Applications. 42 (12): 5056–5064. doi:10.1016/j.eswa.2015.02.046.

[21] Olya, Mohammad Hessam (2014). "Finding shortest path in a combined exponential – gamma probability distribution arc length". International Journal of Operational Research. 21 (1): 25–37. doi:10.1504/IJOR.2014.064020.

[22] Olya, Mohammad Hessam (2014). "Applying Dijkstra's algorithm for general shortest path problem with normal probability distribution arc length". International Journal of Operational Research. 21 (2): 143–154. doi:10.1504/IJOR.2014.064541.

[1]

[2]

[3]

[4]

[5]

[6]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[22]

Search

최단 경로 문제

네임스페이스

더

목차

정의.

알고리즘

단일 소스 최단 경로

무방향 그래프

가중치 없는 그래프

유도 비순환 그래프(DAG)

음수가 아닌 가중치를 갖는 유도 그래프

음수 주기가 없는 임의의 가중치를 가진 유도 그래프

음수 주기의 임의 가중치를 갖는 유도 그래프

임의의 가중치를 갖는 평면 방향 그래프

모두 쌍으로 구성된 최단 경로

무방향 그래프

유향 그래프

적용들

도로망

관련 문제

제약이 있는 경로

부분 관측 가능성

전략적 최단 경로

네거티브 사이클 검출

선형 프로그래밍 공식

반고리에 관한 일반적인 대수적 프레임워크: 대수적 경로 문제

확률적 시간 의존 네트워크에서의 최단 경로

「」를 참조해 주세요.

레퍼런스

메모들

참고 문헌

추가 정보

Search

최단 경로 문제

정의.

알고리즘

단일 소스 최단 경로

무방향 그래프

가중치 없는 그래프

유도 비순환 그래프(DAG)

음수가 아닌 가중치를 갖는 유도 그래프

음수 주기가 없는 임의의 가중치를 가진 유도 그래프

음수 주기의 임의 가중치를 갖는 유도 그래프

임의의 가중치를 갖는 평면 방향 그래프

모두 쌍으로 구성된 최단 경로

무방향 그래프

유향 그래프

적용들

도로망

관련 문제

제약이 있는 경로

부분 관측 가능성

전략적 최단 경로

네거티브 사이클 검출

선형 프로그래밍 공식

반고리에 관한 일반적인 대수적 프레임워크: 대수적 경로 문제

확률적 시간 의존 네트워크에서의 최단 경로

「 」를 참조해 주세요.

레퍼런스

메모들

참고 문헌

추가 정보

「」를 참조해 주세요.