소형입방옥타헤드론
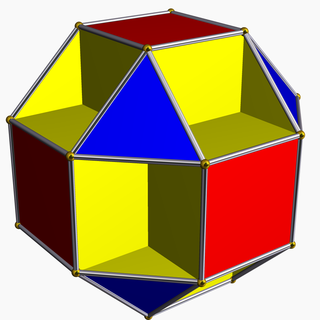
Small cubicuboctahedron| 소형입방옥타헤드론 | |
|---|---|
 | |
| 유형 | 균일성 다면체 |
| 요소들 | F = 20, E = 48 V = 24(수평 = -4) |
| 옆얼굴 | 8{3}+6{4}+6{8} |
| 와이토프 기호 | 3/2 4 4 3 4/3 4 |
| 대칭군 | Oh, [4,3], *432 |
| 색인 참조 | U13, C38, W69 |
| 이중 다면체 | 소형 육각형 이코시트라헤드론 |
| 정점수 |  4.8.3/2.8 |
| 보우어 약자 | 소코 |
기하학에서 작은 입방형 다면체는 U로13 색인된 균일한 별 다면체로, 면 20개(삼각형 8개, 정사각형 6개, 옥타곤 6개)와 가장자리 48개, 꼭지점 24개를 가지고 있다.[1]그것의 꼭지점 모양은 교차된 사각형이다.
작은 입방체옥타헤드론은 롬비큐보옥타헤드론의 한 면이다.그것의 네모난 면과 팔각형의 면은 정육면체 면과 평행한 반면, 삼각형의 면은 팔면체 면의 면과 평행하여, 이름이 큐빅큐브옥타헤드론이다.이 작은 접미사는 앞에서 언급한 방향으로 얼굴이 있는 거대한 입방체(입방체)와 구별하는 역할을 한다.[2]
관련 다면체
그것은 그것의 정점 배열을 잘린 육면체와 공유한다.또한 가장자리 배열을 롬비큐옥타헤드론(삼각형 면과 정사각형 면 6개를 공통으로 함), 작은 롬비헥사헤드론(팔각형 면 공통으로 함)과 공유한다.
 롬비큐옥타헤드론 |  소형입방옥타헤드론 |  작은 rhombihexahedron |  잘린 육면체 |
관련 틸팅
오일러 특성에서 알 수 있듯이 작은 입방정맥아헤드론은 속 3의 토로이드 다면체(위상적으로는 속 3의 표면)이므로 24 정점을 보완한 3개의 다면체 표면을 3-공간으로 흡수하는 (다면체)로 해석할 수 있다.(어떤 꼭지점 근처도 위상학적으로 그림 위에 원뿔이다.몰입에서 일어날 수 없는 re-8리히터 참고문헌은 이 사실을 간과하고 있다는 점에 유의한다.)밑부분의 다면체(자체 교차 부정을 무시함)는 이 표면의 균일한 타일을 정의하고 있으므로, 작은 입방체(cubicuboctahedron)는 균일한 다면체(calified polyheadron)이다.추상 다면체 언어에서 작은 입방체(입방체)는 이 추상적 토로이드 다면체를 충실하게 실현한 것으로, 이는 비생식 다면체라는 뜻이며 같은 대칭군을 가지고 있다는 뜻이다.실제로 이 타일링이 있는 추상속 3 표면의 모든 자동형은 유클리드 공간의 등각계에 의해 실현된다.
더 높은 속 표면(genus 2 이상)은 음의 일정한 곡률(균일화 정리)의 지표를 인정하고, 결과 리만 표면의 보편적 커버는 쌍곡면이다.쌍곡면의 해당 타일링에는 정점 그림 3.8.4.8(삼각, 팔각, 사각, 팔각)이 있다.표면이 적절한 곡률 측정기준 = -1이 주어진 경우 피복지도는 국부 등각도(local isometry)이므로 추상 정점 수치는 동일하다.이 타일링은 Wythoff 기호 3 4 4 4로 나타낼 수 있으며, 오른쪽에 묘사되어 있다.
대안으로 보다 미묘하게 각 사각면을 2개의 삼각형으로, 각 팔각면을 6개의 삼각형으로 잘라서 작은 입방정형(입방정형)은 3개의 표면이 56개의 정삼각형으로 배열되어 각각 도 7과 24개의 정점에서 만나는 것을 비정기적으로 색칠한 것으로 해석할 수 있다.[3]이 정규 타일링은 클라인 쿼트릭의 타일링, 가장 대칭적인 메트릭(이 타일링의 자동모형)을 가진 3개 속 표면의 타일링이며, 이 표면의 방향 유지 자동모형 그룹은 투영 특수 선형 그룹 PSL(2,7)에 이형성이며, 동등하게 GL(3,2) 또는 그 안에 해당하기 때문에 중요하다.168개 그룹의 모든 방향 지시 등위계).작은 입방형 다면체는 24개의 방향 유지 대칭만 가지고 있기 때문에(모든 추상적 자동화가 유클리드 이소계에 의해 실현되는 것은 아님) 이 추상적 다면체의 실현이 아니라는 점에 유의하십시오. – 작은 입방형 다면체의 등방체는 삼각형 타일링뿐만 아니라 색소도 보존하므로, 따라서 적절한 하위면이다.등위계 전집단의 무리
쌍곡면(범용 덮개)의 해당 타일링은 순서 7 삼각 타일링이다.클라인 쿼티크의 자동형 집단은 마티유 그룹 M을24 산출하기 위해 (다면체의 대칭으로 실현되지 않는 대칭성, 즉 "제곱과 옥타헤드라를 이등분하는 가장자리의 두 끝점을 바꾸는 것"에 의해) 증강될 수 있다.[4]
참고 항목
참조
- ^ Maeder, Roman. "13: small cubicuboctahedron". MathConsult.
{{cite web}}: CS1 maint : url-status (링크) - ^ Webb, Robert. "Small Cubicuboctahedron". Stella: Polyhedron Navigator.
{{cite web}}: CS1 maint : url-status (링크) - ^ a b (리히터) 다면체의 각 면은 타일링에 있는 여러 면으로 구성되므로 "색상"이라는 설명에 따라 두 개의 삼각형 면이 사각형 얼굴 등을 구성한다는 점에 유의하십시오.
- ^ (리히터)
- Richter, David A., How to Make the Mathieu Group M24, retrieved 2010-04-15





