텐세그리티

스테레오 이미지

오른쪽 프레임

왼쪽 프레임

크로스 아이 뷰()

병렬 보기()

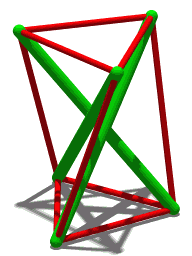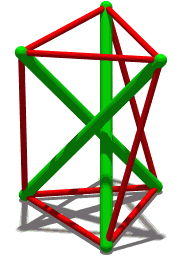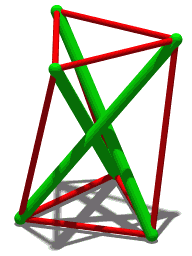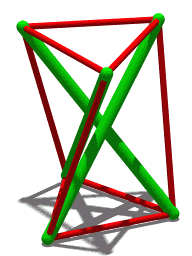
애니메이션 4개의 압축 부재를 가진 유사한 구조입니다.

텐션그레이티, 텐션 완전성 또는 플로팅 압축은 연속 장력의 네트워크 내에서 압축된 격리된 컴포넌트 시스템에 기초한 구조 원리로, 압축된 부재(보통 막대 또는 스트럿)가 서로 접촉하지 않도록 배치되어 있으며, 프리스트 텐션된 부재(보통 케이블 또는 힘줄)s) 시스템을 ^[1]공간적으로 설명한다.

이 용어는 1960년대에 Buckminster Fuller에 의해 "tensional ^[2]integrity"의 합성어로 만들어졌다.텐세그리티의 다른 종류인 부동압축은 구성주의 화가 케네스 스넬슨이 주로 사용했다.

개념.

텐세그리티 구조는 다음과 같은 몇 가지 단순한 설계 패턴의 조합을 기반으로 합니다.

• 순수한 압축 또는 순수한 장력으로 하중을 가하는 부재. 즉, 케이블이 무너지거나 로드가 고정되는 경우에만 구조물이 기능하지 않습니다.이를 통해 각 부재의 재료 특성 및 단면 형상을 해당 부재가 전달하는 특정 하중에 맞게 최적화할 수 있습니다.
• 프리로드 또는 텐션 프리스트레스를 사용하면 케이블은 항상 장력을 유지하여 구조 무결성을 유지할 수 있습니다.
• 구조물에 대한 응력이 증가해도 부재가 장력/압축 상태를 유지할 수 있도록 하는 기계적 안정성.케이블 장력이 증가하면 구조도 더 단단해집니다.

이러한 패턴으로 인해 구조 부재는 굽힘 모멘트를 경험하지 않으며 시스템 내에 전단 응력이 없습니다.이는 질량과 구성 요소의 단면에 대해 예외적으로 강하고 견고한 구조를 만들어 낼 수 있습니다.적어도 일부 텐션 그레이티 구조의 로딩은 보조 응답과 음의 포아송 비율을 유발한다(예: T3 프리즘 및 6 스트럿 텐션 그레이티 20면체).

1951년판 스카일론에서 볼 수 있는 긴장감의 개념적 구성 요소.양 끝에 3개씩 6개의 케이블이 탑을 고정합니다.하부에 접속되어 있는 3개의 케이블에 의해서, 그 위치가 「정의」됩니다.나머지 3개의 케이블은 단순히 수직 상태를 유지하고 있습니다.

3로드 텐세그리티 구조(오른쪽 참조)는 이 단순한 구조 위에 구축되어 있습니다.각 녹색 막대의 끝은 Skylon의 상단과 하단을 닮았습니다.두 케이블 사이의 각도가 180°보다 작으면 로드 위치가 잘 정의됩니다.안정성을 위해 필요한 케이블은 최소 3개이지만, 각 노드에 심미적인 목적이나 안정성을 높이기 위해 케이블을 추가할 수 있습니다.예를 들어, Snelson의 Needle Tower는 각각 5개의 케이블에 연결된 노드를 사용하여 작성된 반복 패턴을 사용합니다.

Eleanor Heartney는 ^[3]이러한 구조의 중요한 미적 특성으로 시각적 투명성을 지적합니다.Korkmaz 등는 경량 텐세그리티 구조가 적응형 ^[4][5]아키텍처에 적합하다고 주장해 왔습니다.

적용들

Tensegrities는 1960년대 Maciej Gintowt와 Maciej Krasiskiski가 Spodek 아레나 콤플렉스(폴란드 Katowice)를 최초로 텐세그리티 원칙을 채택한 주요 구조물 중 하나로 설계하면서 건축에 응용이 증가했습니다.지붕은 둘레를 지탱하는 케이블 시스템에 의해 견제되는 경사면을 사용합니다.텐세그리티 원칙은 데이비드 가이거의 서울 올림픽 체조 경기장(1988년 하계 올림픽)과 조지아 돔(1996년 하계 올림픽)에서도 사용되었다.탬파베이레이스의 홈구장인 트로피카나 필드도 큰 텐션 구조로 지탱되는 돔 지붕을 가지고 있다.

2009년 10월 4일, 호주 퀸즐랜드의 브리즈번 강을 가로질러 쿠릴파 다리가 개통되었다.텐션그리티의 원리에 기초한 멀티마스트 케이블스테이 구조로서 현재 세계에서 가장 큰 텐션그리티 브리지입니다.

2000년대 초부터, 텐세그리티는 가볍고 탄력적인 로봇을 설계할 수 있는 가능성 때문에 로봇 공학자들의 관심을 끌어왔다.수많은 연구들이 텐제리티 로봇,^[6] 생물 모방 로봇,^[7][8] 모듈러 소프트 ^[9]로봇을 조사했다.가장 유명한 텐션그리티 로봇은 현재 NASA 에임스에서 개발 중인 6bar 텐션그리티 구조를 이용한 우주 탐사 로봇 슈퍼볼봇이다.^[10]

생물학

바이오텐시그리티, 닥터에 의해 만들어진 용어입니다.Stephen Levin은 생물학적 ^[11]구조에 텐세그리티 원리를 확장 이론적으로 적용한 사람이다.근육, 뼈, 근막, 인대와 힘줄, 또는 단단하고 탄력 있는 세포막과 같은 생물학적 구조는 긴장된 부분과 압축된 부분의 일치에 의해 튼튼해진다.근골격계는 근육과 결합조직의 ^[12]연속적인 네트워크로 구성되며, 반면 뼈는 전기적 자극을 통해 생체 내 긴장을 유지하는 반면, 뼈는 불연속적인 압박 지지대를 제공한다.레빈은 인간의 척추도 긴장 구조라고 주장하지만 구조적인 관점에서 이 이론을 뒷받침할 수는 없다.^[13]

도날드 E. 잉거는 분자생물학에서 ^[14]관찰된 수많은 현상을 설명하기 위해 긴장 이론을 개발했다.예를 들어, 적용된 압력에 대한 반응이든 기판과의 상호작용이든 세포의 표현된 모양은 모두 세포의 세포골격을 긴장도로 표현함으로써 수학적으로 모델링할 수 있다.또한 자연에서 발견되는 기하학적 패턴(DNA의 나선, 볼복스의 측지 돔, 벅민스터풀레렌 등)은 화합물, 단백질 ^[15]및 심지어 장기의 자발적 자기집합에 대한 텐세그리티의 원리를 적용하여 이해할 수 있다.이러한 관점은 생물학적 프레임워크 내에서 불활성 물질과의 비교가 생리 ^[16]과학 내에서 널리 받아들여지는 전제가 없음에도 불구하고, 긴장도의 긴장-압축 상호작용이 안정성을 유지하고 구조적 복원력을 달성하는 데 필요한 물질을 어떻게 최소화하는가에 의해 뒷받침된다.따라서 자연선택 압력은 긴장된 방식으로 조직된 생물학적 시스템에 유리할 수 있습니다.

Ingber의 설명:

풀러의 돔이든 스넬슨의 조각이든 이러한 구조물에 장력을 주는 부재는 인접한 부재들 사이의 최단 경로를 계획합니다(따라서 정의상 지리학적으로 배열되어 있습니다).장력은 자연스럽게 두 점 사이의 최단 거리에 걸쳐 전달되므로 텐세그리티 구조의 부재는 응력에 가장 잘 견딜 수 있도록 정확하게 배치됩니다.이러한 이유로 텐세그리티 구조는 최대 ^[14]강도를 제공합니다.

발생학에서 리처드 고든은 배아 분화파가 세포 골격이 '세포 상태 분할기'^[18]라고 불리는 세포 끝의 쌍안정성 긴장 구조에서 조립되는 '분화의 ^[17]기관'에 의해 전파된다고 제안했다.

기원과 미술사

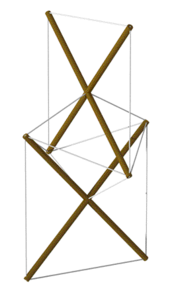
긴장감의 기원은 논란의 ^[20]여지가 있다.스킨 온 프레임 카약이나 쇼지 등 많은 전통적인 구조물은 비슷한 방식으로 장력과 압축 요소를 사용한다.

러시아 화가 비아차슬라프 콜레이추크는 긴장감이라는 개념이 ^[21]1921년 러시아 구성주의 주요 전시회에 일부 작품을 기고한 라트비아계 소련 전위예술가 칼 이오간손스(러시아어로 카를 이오간손과 같은 독일인)에 의해 처음 발명됐다고 주장했다.콜레이추크의 주장은 1921년 구성주의 ^[22]전시회에서 마리아 고프에 의해 뒷받침되었다.Snelson은 구성주의자들이 그의 작품에 영향을 미쳤다고 인정했다.^[23]프랑스 엔지니어 David Georges Emmerich는 Karlis Johansons의 작품(및 산업 디자인 아이디어)이 어떻게 긴장감 ^[24]개념을 예견하는 것처럼 보였는지에 대해서도 언급했다.

1948년 예술가 케네스 스넬슨은 블랙마운틴 칼리지(버크민스터 풀러가 강의하던 곳) 등에서 예술탐구를 거쳐 혁신적인 엑스피스를 제작했다.몇 년 후, "텐세그리티"라는 용어는 측지 돔으로 가장 잘 알려진 풀러에 의해 만들어졌다.Fuller는 경력을 통해 다이맥시온 ^[25]하우스의 골격과 같은 인장 부품을 작업에 통합하는 실험을 했습니다.

1948년 스넬슨의 혁신은 풀러로 하여금 즉시 스넬슨에서 돛대를 제작하도록 자극했다.1949년, Fuller는 그 기술을 바탕으로 텐션그리티-이십면체를 개발했고 그와 그의 학생들은 빠르게 더 많은 구조물을 개발했고 그 기술을 돔 건축에 적용했다.잠시 후, 스넬슨은 또한 긴장감 개념을 바탕으로 많은 조각품을 제작했다.그의 주요 작품은 1959년 현대미술관에서 중요한 전시회가 열리면서 시작되었다.MOMA 전시회에서 Fuller는 돛대와 그의 다른 ^[26]작품들을 보여주었다.이번 전시회에서 스넬슨은 풀러 및 전시 주최 측과 마스트의 크레딧에 대해 논의한 후 ^[27]유리창에 작품을 전시하기도 했다.

스넬슨의 가장 잘 알려진 작품은 1968년 18미터 높이의 니들 타워이다.

안정성.

텐세그리티 프리즘

3로드 텐션그리티 구조(3방향 프리즘)는 주어진 (공통) 길이의 압축 부재 "로드"(총 3개)와 로드 끝을 연결하는 텐션 케이블 "텐돈"(총 6개)의 주어진 (공통) 길이에 대해 로드 상단과 로드 상단을 연결하는 힘줄의 (공통) 길이에 대한 특정 값이 있습니다.구조물이 안정된 형태를 유지하도록 하는 인접 막대 바닥.이러한 구조에서는 로드톱에 의해 형성되는 삼각형과 로드바닥에 의해 형성되는 삼각형이 서로 5µ/6(라디안)^[28]의 각도만큼 회전하고 있음을 증명하기 쉽다.

술탄 등은 여러 2단계 텐션 구조의 안정성("억제성")을 분석한다.^[29]

텐세그리티 이코사면체

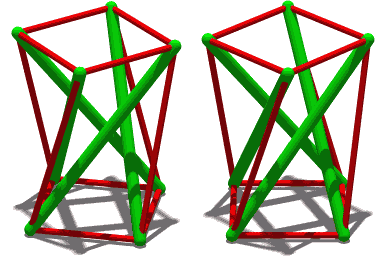
1949년 ^[30]스넬슨에 의해 처음 연구된 텐세그리티 20면체는 제센의 20면체라고 불리는 다면체의 가장자리를 따라 스트럿과 힘줄이 있다.이동성은 ^[31][32]미미하지만 안정적인 구조입니다.이를 확인하려면 원점을 중심으로 한 변 길이가 2d인 입방체를 고려합니다.각 스트럿이 면의 한 모서리에 평행하고 면 중앙에 오도록 각 입방체 면의 평면에 길이 2l의 스트럿을 배치합니다.또한 각 스트럿은 큐브의 반대쪽 면에 있는 스트럿과 평행해야 하지만 다른 모든 스트럿과 직교해야 합니다.하나의 스트럿의 데카르트 좌표가${\displaystyle }$($,$, $l)$ {$displaystyle$$(0, d,$ l)}${\displaystyle }$및$$ (${\displaystyle 0,}$ ${\displaystyle d,}$ $l$ {$displaystyle$$(0,$d, l)}인 경우 병렬 스트럿의 좌표는 각각 (${\displaystyle 0,}$ $, l)$${\displaystyle }$및 0${\displaystyle ,}$ ${\displaystyle \mathrm{display}}$ $style$ ($0,$ d${\displaystyle ,}$ $)$입니다.ces)는 예를 들어 (${\displaystyle 0,}$ ${\displaystyle d,l}$ ) ${\displaystyle \to }$ ( ${\displaystyle d}$,${\displaystyle l}$ ,${\displaystyle 0}$ ) ${\displaystyle \to }$ (${\displaystyle l}$ ,${\displaystyle 0}$ ,${\displaystyle d}$) { $displaystyle ( 0$ , $d$, l )\ $rightarrow ( d$ ,$l$ ,$0$ )\ $rightarrow ($ d ,$l$ , l ,$0$ )} (입방체 대각선의 회전대칭)}$$ 등${\displaystyle }$좌표를 환산하여 구합니다.

인접한 두 정점(0, d, l)과 (d, l, 0) 사이의 거리 s는 다음과 같습니다.

$${\displaystyle s^{2}=(d-l)^{2}+l^{2}=2\left(d-{\frac {1}{2}},l\right)^2}+{\frac {3}{2},l^{2}}$$

이 그림은s $>$ 2 l {\$sqrt {frac {3}{2}},l$의 주어진 길이 2 l의 스트럿과 (인접하는 정점을 연결하는) 힘줄로 구성되어 있다고 가정합니다.이 관계를 통해 d에는 두 가지 가능한 값이 있음을 알 수 있습니다.하나는 스트럿을 서로 밀어냄으로써 실현되고 다른 하나는 그것들을 분리함으로써 실현됩니다.특히 $s{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle \sqrt{\frac{3}{}}}$ ${\displaystyle 2\sqrt{}}$l {\$displaystyle$ s$= sq$ { $frac$ ${$$3}$ {2$},l}$ 두$$ $극단$이 일치하고, ${\displaystyle d\frac{\mathrm{}}{}}$ ${\displaystyle =}$ ${\displaystyle \frac{1}{}}$ l { $displaystyle$ d=$1 {$1} {2$}},$l$\}$의 경우, 이 수치는 안정된 긴장도 20면체이다.이 매개변수 선택은 정점에 제센의 20면체의 위치를 제공한다. 정점은 d$${\$displaystyle$ d$$$}$와$$l {\$displaystyle$ l$}$의 $비율$이 2가 아닌 황금 비율이 되는 정규 20면체와 다르다.그러나 두 좌표 집합은 나선형 수축/팽창 변환에 의해 연결된 입방체부터 팔면체(한계 케이스)까지의 연속된 위치 패밀리를 따라 놓인다.이 정육면체의 운동학은 긴장도 20면체의 운동 기하학이다.이것은 H. S. M^[33]. 콕서터에 의해 처음 설명되었고 나중에 벅민스터 ^[34][35]풀러에 의해 "지터버그 변환"이라고 불렸습니다.

텐션그리티 20면체는 위의 관계의 극점을 나타내기 때문에, 극소 이동성을 가진다: 힘줄의 길이 s의 작은 변화(예를 들어 힘줄의 스트레칭에 의해)는 ^[36]스트럿의 거리 2d의 훨씬 큰 변화를 초래한다.

특허

• 미국 특허 3,063,521, "텐실 무결성 구조", 1962년 11월 13일, 벅민스터 풀러.
• 프랑스 특허 No. 1,377,290, "Construction de Leosaux Autotendants", 1964년 9월 28일, David Georges Emmerich.
• 프랑스 특허 No. 1,377,291, "Structures Linéairs Autotendants", 1964년 9월 28일 데이비드 조르주 엠메리히.
• 미국 특허 3,139,957, "서스펜션 빌딩", 1964년 7월 7일 벅민스터 풀러.
• 미국 특허 3,169,611, "Continuous Tension, Indincuous Compression Structure", 1965년 2월 16일, Kenneth Snelson.
• 미국 특허 3,866,366 "비대칭 텐션 무결성 구조", 1975년 2월 18일 벅민스터 풀러.

기본 시제 구조

• 

  가장 단순한 텐션 구조인 3-프리즘

• 

  또 하나의 3-프리즘

• 

  유사한 구조이지만 4개의 압축 부재가 있는 구조

• 

  칼 이오간손의 텐세그리티 프리즘, 1921년^{[gallery 1]}

• 

  Buckminster Fuller, Tensegrity 이십면체, 1949^{[gallery 2]}

• 

  프란체스코 델라 살라, 1952년^{[gallery 3]} 텐세그리티 사면체

• 

  Tensegrity X-모듈 사면체, 케네스 스넬슨, 1959년^{[gallery 4]}

텐세그리티 구조

• 

  케네스 스넬슨의 니들 타워 예술 조각품입니다.

• 

  정원 말뚝과 나일론 끈으로 만든 텐세그리티 돔, 2009년.

• 

  콜카타의 사이언스 시티에서 12m 높이의 텐션 구조물이 전시되어 있습니다.

• 

  2015년 버닝맨 지역행사 아프리카번에서 건립된 텐세이트 구조를 포함한 모래시계 타워 아트 조형물 '디세이트'

「 」를 참조해 주세요.

• 벅민스터 풀러에 의해 명명된 거대한 하늘을 떠다니는 긴장구인 구름 9
• 하이퍼볼로이드 구조 – 무한 2차 표면형 건물 또는 워크 유형
• 행위자 상호작용 이론
• 안장 지붕
• 공간 프레임 – 견고한 3차원 하중 지지 트러스 구조
• 시너제틱스
• 텐세리티
• 인장 구조
• 얇은 셸 구조
• 정육면체의 운동학 – 정육면체의 대칭 변환으로 관련된 균일한 다면체, 텐션그리티 20면체의 운동 기하학

메모들

레퍼런스

참고 문헌

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 협조해 주십시오.(2009년 3월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍에 대해 알아보세요)

• Fuller, R. Buckminster (1961). "Tensegrity". Portfolio and Art News Annual (4): 112–127, 144, 148.
• — (1982) [1975]. Synergetics: Explorations in the Geometry of Thinking. Vol. I. Macmillan. ISBN 978-0-02-065320-2.
• — (1983) [1979]. Synergetics 2: Further Explorations in the Geometry of Thinking. Vol. 2. Macmillan. ISBN 978-0-02-092640-5. 온라인.
• —; Marks, Robert W. (1973) [1960]. The Dymaxion World of Buckminster Fuller. Anchor Books. Figs. 261–280. ISBN 978-0385018043. Fuller의 관점에서 볼 때 텐션의 범위에 대한 좋은 개요와 대부분의 경우 신중한 속성을 가진 초기 구조에 대한 흥미로운 개요.
• Kenner, Hugh (1976). Geodesic Math and How to Use It. University of California Press. ISBN 978-0520029248. 2003년 ISBN 0520239318 전재.이곳은 시제도의 수학과 모델을 만들기에 좋은 출발점입니다.
• Gómez-Jáuregui, Valentin (2007). Tensegridad. Estructuras Tensegríticas en Ciencia y Arte (in Spanish). Santander: Universidad de Cantabria. ISBN 978-84-8102-437-1.
• — (2010). Tensegrity Structures and their Application to Architecture. Santander: Servicio de Publicaciones de la Universidad de Cantabria. ISBN 978-84-8102-575-0.
• Gough, Maria (Spring 1998). "In the Laboratory of Constructivism: Karl Ioganson's Cold Structures". October. 84: 90–117. doi:10.2307/779210. JSTOR 779210.
• Juan, S. J.; Tur, J M (July 2008). "Tensegrity frameworks: Static analysis review". Mechanism and Machine Theory. 43 (7): 859–81. CiteSeerX 10.1.1.574.7510. doi:10.1016/j.mechmachtheory.2007.06.010.
• Korkmaz, Sinan; Bel Hadj Ali, Nizar; Smith, Ian F.C. (June 2011). "Determining Control Strategies for Damage Tolerance of an Active Tensegrity Structure" (PDF). Engineering Structures. 33 (6): 1930–1939. CiteSeerX 10.1.1.370.6243. doi:10.1016/j.engstruct.2011.02.031. Archived from the original (PDF) on 29 September 2011.
• —; —; — (January 2012). "Configuration of Control System for Damage Tolerance of a Tensegrity Bridge". Advanced Engineering Informatics. 26 (1): 145–155. doi:10.1016/j.aei.2011.10.002.
• Lalvani, Haresh, ed. (1996). "Origins of Tensegrity: Views of Emmerich, Fuller and Snelson". International Journal of Space Structures. 11 (1–2): 27–55. doi:10.1177/026635119601-204. S2CID 114004009.
• Souza, Thales R.; Fonseca, Sérgio T.; Gonçalves, Gabriela G.; Ocarino, Juliana M.; Mancini, Marisa C. (October 2009). "Prestress revealed by passive co-tension at the ankle joint". Journal of Biomechanics. 42 (14): 2374–80. doi:10.1016/j.jbiomech.2009.06.033. PMID 19647832.

추가 정보

• Edmondson, Amy (2007)."충분한 설명", Emergent World LLC
• Forbes, Peter (2010) [2006]. "9. The Push and Pull Building System". The Gecko's Foot: How Scientists are Taking a Leaf from Nature's Book. Harper Collins. pp. 197–230. ISBN 978-0-00-740547-3.
• Hanaor, Ariel (1997). "13. Tensegrity: Theory and Application". In Gabriel, J. François (ed.). Beyond the Cube: The Architecture of Space Frames and Polyhedra. Wiley. pp. 385–408. ISBN 978-0-471-12261-6.
• Masic, Milenko; Skelton, Robert E.; Gill, Philip E. (August 2005). "Algebraic tensegrity form-finding". International Journal of Solids and Structures. 42 (16–17): 4833–4858. doi:10.1016/j.ijsolstr.2005.01.014. 그들은 시제도의 선형 변환 또한 시제도의 것이라는 놀라운 결과를 제시합니다.
• Morgan, G.J. (2003). "Historical Review: Viruses, Crystals and Geodesic Domes". Trends in Biochemical Sciences. 28 (2): 86–90. doi:10.1016/S0968-0004(02)00007-5. PMID 12575996.
• Motro, R. (1992). "Tensegrity Systems: The State of the Art". International Journal of Space Structures. 7 (2): 75–84. doi:10.1177/026635119200700201. S2CID 107820090.
• Pugh, Anthony (1976). An Introduction to Tensegrity. University of California Press. ISBN 978-0-520-03055-8. Archived from the original on 4 May 2008. Retrieved 9 May 2008.
• Snelson, Kenneth (November 1990). "Letter to R. Motro". International Journal of Space Structures.
• 빌나이, 오렌(1990).Cable Nets and Tensegric Shells: 분석 및 설계 응용 프로그램, 뉴욕: Ellis Horwood ^{[ISBN missing]}Ltd.
• Wang, Bin-Bing (1998). "Cable-strut systems: Part I – Tensegrity". Journal of Constructional Steel Research. 45 (3): 281–89. doi:10.1016/S0143-974X(97)00075-8.
• 윌켄, 티모시(2001).선물 시제, Trust^{[ISBN missing]} Mark를 찾고 있습니다.

외부 링크

• 스위스 연방공과대학(EPFL), 응용컴퓨팅기계연구소(IMAC)의 텐세그리티 분야 과학 출판물
• Stephen Levin's Biotensegrity 사이트 정형외과 의사가 바이러스에서 척추동물에 이르는 생물학적 구조의 긴장역학에 대한 여러 논문.