튜링 패턴

Turing pattern
튜링 패턴의 세 가지 예
튜링 패턴을 생성하는 6개 상태

튜링 패턴은 영국 수학자 앨런 튜링이 1952년 '모포제네시스의 화학적 기반'이라는 논문을 통해 소개한 개념으로 줄무늬나 반점 등 자연의 패턴이 어떻게 동질적이고 균일한 상태에서 자연적으로 자율적으로 발생할 수 있는지를 기술하고 있다.[1] 튜링은 고전적인 논문에서 두 개의 확산성 물질이 서로 상호작용하는 시스템의 행동을 조사했고, 그러한 시스템이 무작위적이거나 거의 균일한 초기 조건에서도 공간적으로 주기적인 패턴을 생성할 수 있다는 것을 발견했다.[2] 튜링은 결과적인 와블리크 패턴이 형태생식의 화학적 기초라는 가설을 세웠다.[2]

튜링 패터닝은 종종 다른 패턴과 결합하여 발견된다: 척추동물 사지 발달은 튜링 패터닝을 보완적 패턴과 중첩시키는 많은 표현형들 중 하나이다(이 경우 프랑스 국기 모델).[3]

개념

튜링 분기 패턴
거대한 복어의 자연스러운 튜링 패턴의 예

형태생식에 대한 반작용-확산 이론인 원론은 이론 생물학에서 중요한 모델로 작용해 왔다.[4] 반응-확산 시스템은 패턴 형성을 위한 프로토타입 모델로서 많은 관심을 끌었다. 앞면, 육각형, 나선형, 줄무늬, 방산용액과 같은 패턴은 튜링 유사 반응-디퓨전 방정식의 해결책으로 발견된다.[5]

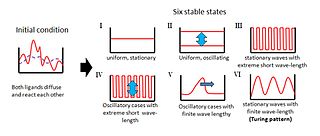
튜링은 균일하게 분포된 두 물질(P와 S)이 상호작용하여 형태생성 동안 안정적인 패턴을 생성하는 모델을 제안했다. 이러한 패턴은 두 물질의 농도에서의 지역적 차이를 나타낸다. 그들의 상호작용은 임의의 혼돈으로부터 질서 있는 구조를 만들어 낼 것이다.[6]

튜링의 모델에서 물질 P는 물질 S뿐만 아니라 더 많은 물질 P의 생산을 촉진한다. 그러나 물질 S는 물질 P의 생성을 억제하며, 만일 S가 P보다 더 쉽게 확산되면 물질 P에 대해 농도 차이의 날카로운 파동이 생성된다. 튜링 모델의 중요한 특징은 물질의 분포에 있는 특정 파장은 증폭되는 반면 다른 파장은 억제된다는 것이다.[6]

매개변수는 고려 중인 물리적 시스템에 따라 달라진다. 어류 피부 색소 침착의 맥락에서 관련 방정식은 세 가지 장 반응-확산인데, 여기에는 선형 파라미터가 색소 침착 세포 농도와 연관되어 있고 확산 파라미터가 모든 장에 대해 동일하지 않다.[7] 염료 도량형 액체 결정에서 액정 행렬의 광이소체화 과정은 두 가지 분야(액정 순서 파라미터와 아조-디아의 시스-이소머 농도)의 반응-확산 방정식으로 설명된다.[8] 이 시스템들은 화학반응과 확산과정에 대해 매우 다른 물리적 메커니즘을 가지고 있지만 현상학적 수준에서 두 시스템 모두 동일한 성분을 가지고 있다.

튜링과 같은 패턴은 확산성 형태균의 고전적 요구사항이 없는 유기체 개발에서 발생하는 것으로 입증되었다. 병아리와 쥐의 배아 발달에 관한 연구는 깃털과 털의 전구체의 패턴이 형태소 전구체 없이 형성될 수 있고, 그 대신 피부 밑에 깔려 있는 중피세포의 자가 분리를 통해 생성된다는 것을 시사한다.[9][10] 이러한 경우, 균일한 세포 집단은 세포 자체의 기계적 특성과 주변 외부 세포 환경의 강성에 따라 정기적으로 패턴화된 골재를 형성할 수 있다. 이러한 종류의 세포 골재에 대한 규칙적인 패턴은 원래 조지 오스터에 의해 공식화된 이론적 모델에서 제안되었는데, 세포 운동성과 강성의 변경이 균일한 세포 분야로부터 다른 자기 발현 패턴을 발생시킬 수 있다고 가정했다.[11] 이 패턴 형성 모드는 고전적인 반응-확산 시스템과 함께 작용하거나 생물학적 발달에서 패턴을 생성하기 위해 독립적으로 작용할 수 있다.

생물 유기체에서뿐만 아니라 튜링 패턴은 다른 자연계에서 발생한다.[12][13] 예를 들어 모래에서 형성된 바람 패턴, 비스무트 결정의 성장 중에 형성될 수 있는 원자 규모의 반복 파동, 은하 원반에서 물질의 불균일한 분포. 형태생식과 튜링패턴에 대한 튜링의 아이디어는 수년간 잠잠했지만, 그것들은 이제 수학적 생물학에 대한 많은 연구에 영감을 주고 있다.[14] 그것은 발달 생물학에서 주요한 이론이다; 그것은 형태생식에 대한 근본적인 질문에 대한 답을 제공하기 때문에 튜링 모델의 중요성은 명백하다. "공간 정보는 유기체에서 어떻게 생성되는가?"[2]

튜링 패턴은 루지아토-레페버 방정식으로 입증된 비선형 광학에서도 생성될 수 있다.

생물학적 응용

사지 봉오리 원위 확장의 효과 시뮬레이션

개발 시스템에서 스폿과 줄무늬 같은 패턴의 발생기로서 점점 더 주목을 받게 된 메커니즘은 1952년 튜링에 의해 기술된 화학 반응-분해 과정과 관련이 있다. 이것은 마인하르트와 지러에 의해 생물학적 "로컬 자동 활성화-측면 억제(LALI)" 프레임워크에서 도식화되었다.[16] LALI 시스템은 공식적으로 반응-확산 시스템과 유사하지만 생물학적 적용에 더 적합하다. 왜냐하면 그것들은 단순한 화학반응이 아닌 세포 "반응기"에 의해 활성제 및 억제제 용어가 매개되는 경우를 포함하고 있고,[17] 공간적 전송은 단순한 확산과 더불어 메커니즘에 의해 매개될 수 있기 때문이다.[18] 이 모델들은 다른 예들 중에서 사지 형성과 치아 발달에 적용될 수 있다.

반응-확산 모델을 사용하여 유전자 발현 패턴의 차이를 바탕으로 생쥐와 볼륨에서 치아의 정확한 위치를 예측할 수 있다.[6] 이 모델은 쥐와 볼빨간 이빨 사이의 유전자 발현 차이, 치아의 신호 중심, 에나멜 매듭, 비밀 BMP, FGFs와 쉿을 설명하는 데 사용될 수 있다. 쉿과 FGF는 BMP 생산을 억제하는 반면, BMP는 더 많은 BMP의 생산과 그들 자신의 억제제의 합성을 모두 자극한다. BMP는 상피 분화를 유도하고 FGF는 상피 성장을 유도한다.[19] 그 결과는 치아의 형태가 변함에 따라 변하는 유전자 활동의 패턴이며, 그 반대도 마찬가지다. 이 모델에서 마우스와 볼 어금니의 큰 차이는 BMP와 쉿 단백질의 결합 상수와 확산 속도의 작은 변화로 발생할 수 있다. BMP4의 확산률이 소폭 증가하고 그 억제제의 강한 결합 상수는 이빨 성장의 공극 패턴을 마우스의 공극 패턴으로 바꾸기에 충분하다.[19][20]

참고 항목

참조

  1. ^ Turing, Alan (1952). "The Chemical Basis of Morphogenesis" (PDF). Philosophical Transactions of the Royal Society of London B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012. JSTOR 92463. S2CID 120437796.
  2. ^ a b c Kondo, Shigeru (7 February 2017). "An updated kernel-based Turing model for studying the mechanisms of biological pattern formation". Journal of Theoretical Biology. 414: 120–127. Bibcode:2017JThBi.414..120K. doi:10.1016/j.jtbi.2016.11.003. ISSN 0022-5193. PMID 27838459.
  3. ^ Sharpe, James; Green, Jeremy (2015). "Positional information and reaction-diffusion: two big ideas in developmental biology combine". Development. 142 (7): 1203–1211. doi:10.1242/dev.114991. PMID 25804733.
  4. ^ Harrison, L. G. (1993). "Kinetic Theory of Living Pattern". Endeavour. Cambridge University Press. 18 (4): 130–6. doi:10.1016/0160-9327(95)90520-5. PMID 7851310.
  5. ^ Kondo, S.; Miura, T. (23 September 2010). "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation". Science. 329 (5999): 1616–1620. Bibcode:2010Sci...329.1616K. doi:10.1126/science.1179047. PMID 20929839. S2CID 10194433.
  6. ^ a b c Gilbert, Scott F., 1949- (2014). Developmental biology (Tenth ed.). Sunderland, MA, USA. ISBN 978-0-87893-978-7. OCLC 837923468.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
  7. ^ Nakamasu, A.; Takahashi, G.; Kanbe, A.; Kondo, S. (11 May 2009). "Interactions between zebrafish pigment cells responsible for the generation of Turing patterns". Proceedings of the National Academy of Sciences. 106 (21): 8429–8434. Bibcode:2009PNAS..106.8429N. doi:10.1073/pnas.0808622106. PMC 2689028. PMID 19433782.
  8. ^ Andrade-Silva, Ignacio; Bortolozzo, Umberto; Clerc, Marcel G.; González-Cortés, Gregorio; Residori, Stefania; Wilson, Mario (27 August 2018). "Spontaneous light-induced Turing patterns in a dye-doped twisted nematic layer". Scientific Reports. 8 (1): 12867. Bibcode:2018NatSR...812867A. doi:10.1038/s41598-018-31206-x. PMC 6110868. PMID 30150701.
  9. ^ Glover, James D.; Wells, Kirsty L.; Matthäus, Franziska; Painter, Kevin J.; Ho, William; Riddell, Jon; Johansson, Jeanette A.; Ford, Matthew J.; Jahoda, Colin A. B.; Klika, Vaclav; Mort, Richard L. (2017). "Hierarchical patterning modes orchestrate hair follicle morphogenesis". PLOS Biology. 15 (7): e2002117. doi:10.1371/journal.pbio.2002117. PMC 5507405. PMID 28700594.
  10. ^ Shyer, Amy E.; Rodrigues, Alan R.; Schroeder, Grant G.; Kassianidou, Elena; Kumar, Sanjay; Harland, Richard M. (2017). "Emergent cellular self-organization and mechanosensation initiate follicle pattern in the avian skin". Science. 357 (6353): 811–815. doi:10.1126/science.aai7868. PMC 5605277. PMID 28705989.
  11. ^ Oster, G. F.; Murray, J. D.; Harris, A. K. (1983). "Mechanical aspects of mesenchymal morphogenesis". Journal of Embryology and Experimental Morphology. 78: 83–125. PMID 6663234.
  12. ^ Fuseya, Yuki; Katsuno, Hiroyasu; Behnia, Kamran; Kapitulnik, Aharon (8 July 2021). "Nanoscale Turing patterns in a bismuth monolayer". Nature Physics. 17 (9): 1031–1036. Bibcode:2021NatPh..17.1031F. doi:10.1038/s41567-021-01288-y. ISSN 1745-2481. S2CID 237767233.
  13. ^ Smolin, Lee (3 December 1996). "Galactic disks as reaction-diffusion systems". arXiv:astro-ph/9612033.
  14. ^ 울리, T. E., 베이커, R. E., 마이니, P. K., 34장 튜링의 형태생성 이론. 인
  15. ^ Zhu, Jianfeng; Zhang, Yong-Tao; Alber, Mark S.; Newman, Stuart A. (28 May 2010). Isalan, Mark (ed.). "Bare Bones Pattern Formation: A Core Regulatory Network in Varying Geometries Reproduces Major Features of Vertebrate Limb Development and Evolution". PLOS ONE. 5 (5): e10892. Bibcode:2010PLoSO...510892Z. doi:10.1371/journal.pone.0010892. ISSN 1932-6203. PMC 2878345. PMID 20531940.
  16. ^ Meinhardt, Hans (2008), "Models of Biological Pattern Formation: From Elementary Steps to the Organization of Embryonic Axes", Multiscale Modeling of Developmental Systems, Current Topics in Developmental Biology, vol. 81, Elsevier, pp. 1–63, doi:10.1016/s0070-2153(07)81001-5, ISBN 978-0-12-374253-7, PMID 18023723
  17. ^ Hentschel, H. G. E.; Glimm, Tilmann; Glazier, James A.; Newman, Stuart A. (22 August 2004). "Dynamical mechanisms for skeletal pattern formation in the vertebrate limb". Proceedings of the Royal Society of London. Series B: Biological Sciences. 271 (1549): 1713–1722. doi:10.1098/rspb.2004.2772. ISSN 0962-8452. PMC 1691788. PMID 15306292.
  18. ^ Lander, Arthur D. (January 2007). "Morpheus Unbound: Reimagining the Morphogen Gradient". Cell. 128 (2): 245–256. doi:10.1016/j.cell.2007.01.004. ISSN 0092-8674. PMID 17254964. S2CID 14173945.
  19. ^ a b Salazar-Ciudad, Isaac; Jernvall, Jukka (March 2010). "A computational model of teeth and the developmental origins of morphological variation". Nature. 464 (7288): 583–586. Bibcode:2010Natur.464..583S. doi:10.1038/nature08838. ISSN 1476-4687. PMID 20220757. S2CID 323733.
  20. ^ Salazar-ciudad, Isaac; Jernvall, Jukka (January 2004). "How different types of pattern formation mechanisms affect the evolution of form and development". Evolution and Development. 6 (1): 6–16. doi:10.1111/j.1525-142x.2004.04002.x. ISSN 1520-541X. PMID 15108813. S2CID 1783730.

참고 문헌 목록