루트가 없는 이진 트리

방선박테리아 종 간의 유사성과 진화사를 나타내는 뿌리 없는 이진수 형태의 분해도.

수학과 컴퓨터 과학에서, 뿌리 없는 이진수 트리는 각 정점이 하나 또는 세 개의 이웃을 갖는 뿌리 없는 트리이다.

정의들

프리 트리 또는 비루트 트리는 주기가 없는 연결된 무방향 그래프입니다.인접 라우터가 1개인 정점은 트리의 잎이고 나머지 정점은 트리의 내부 노드입니다.정점의 정도는 인접하는 수이며, 여러 개의 노드가 있는 트리에서 잎은 1도의 정점이 됩니다.비루트 바이너리 트리는 모든 내부 노드의 등급이 정확히 3인 프리 트리입니다.

어떤 어플리케이션에서는 루트가 없는 바이너리 트리의 서브 타입을 구별하는 것이 타당할 수 있다: 트리의 평면 임베딩은 각 정점에서 에지에 대한 순환 순서를 지정하여 평면 트리로 만드는 것으로 고정될 수 있다.컴퓨터 과학에서 이진 트리는 종종 데이터 구조로 사용될 때 루트와 순서가 매겨지지만, 계층적 클러스터링과 진화적 트리 재구성의 비루트 이진 트리의 적용에서는 순서가 매겨지지 않은 트리가 더 ^[1]일반적입니다.

또한 모든 정점에 별도의 라벨이 있는 나무, 잎에만 라벨이 붙어 있는 나무, 노드에 라벨이 붙어 있지 않은 나무를 구분할 수 있습니다.n개의 잎을 가진 비근원 이진 트리에서 n - 2개의 내부 노드가 존재하므로 모든 노드에 라벨을 붙여야 할 경우 1 - 2n - 1의 정수 집합에서, 잎에만 라벨을 ^[1]붙여야 할 경우 1 - n의 정수 집합에서 라벨을 얻을 수 있습니다.

열거

계층적 클러스터링에서의 애플리케이션 때문에, 비루트 바이너리 트리의 가장 자연스러운 그래프 열거 문제는 n개의 라벨이 붙은 잎과 라벨이 없는 내부 노드를 가진 트리의 수를 세는 것이다.n개의 라벨이 붙은 잎의 비근원 2진수 트리는 n번째 잎을 라벨이 붙은 잎의 비근원 2진수 트리의 가장자리 가운데에 있는 새로운 노드에 접속함으로써 형성될 수 있다.n번째 노드를 부착할 수 있는 가장자리는 2n-5개이므로 n잎의 나무 수는 n-1잎의 나무 수보다 2n-5배 많다.따라서 n개의 레이블이 지정된 잎에 있는 나무 수는 이중 요인입니다.

(\displaystyle (2n-5)!=snfrac {(2n-4)!}{(n-2)!2^{n-2}}}}.}

^[6]

2, 3, 4, 5, ...라는 라벨이 붙은 나뭇잎의 나무 수는

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ...(OEIS의 시퀀스 A001147).

기본적인 동등성

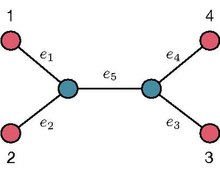
고정 Unrooted Binary Tree(UBT; 비루트 바이너리 트리) T의 리프 투 리프 경로 길이는 특정 리프를 다른 리프로 연결하는 T의 고유 경로에 속하는 에지 수를 인코딩합니다.예를 들어 오른쪽 이미지에 나타난 UBT를 참조하면 리프1과 2 사이의 $p_{1,2}$ $p_{1,2}$ $(\$ 는 $p_{1,2}$ 2인 반면 리프1과 3 사이의 $p_{1,3}$ $p_{1,3}$ (\ $displaystyle p_{1,3})$ 은 $p_{1,3}$ 3이 됩니다.고정 UBT T 상의 특정 리프로부터의 경로 길이 시퀀스는 지정된 리프에서 나머지 모든 리프까지의 경로 길이를 부호화합니다.예를 들어 오른쪽 그림에 표시된 UBT를 참조함으로써 리프 1로부터의 패스렝스 시퀀스는 $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ ( $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , p $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , $4$ ( $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ , $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ 3 $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ ) ( \ $display p_{1} =$ ( $p$ _ { 1, $2$ , p _ { 1, $3$ , $p _ 3$ ) $=$ ( $p$ _ { $1$ , 3 ) $p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)$ = 3 , 3 ) $。$ T의 ng번째 시퀀스 수집.

네 개의 잎이 있는 루트가 없는 이진 트리의 예제

Danielle Catanzaro, Raffaele Pesenti 및 Laurence Wolsey는^[7] n개의 잎으로 주어진 UBT를 인코딩하는 경로 길이 시퀀스 컬렉션이 특정 동등성을 충족해야 한다는 것을 보여주었다.

$p_{i,i}=0$ i $p_{i,i}=0$ $p_{i,i}=0$ $=$ ( $i\in [1,n]$ i $i\in [1,n]$ [ 1, n $i\in [1,n]$ ](\displaystyle $p_{i,i$ }= $0)$ (모든 $p_{i,i}=0$ i) [ $i\in [1,n]$ ](\ $displaystyle$ i $\in [1,n]))$
$p_{i,j}=p_{j,i}$ i , $p_{i,j}=p_{j,i}$ $p_{i,j}=p_{j,i}$ $p_{i,j}=p_{j,i}$ j , $p_{i,j}=p_{j,i}$ $i,j\in [1,n]:i\neq j$ { $i,j\in [1,n]:i\neq j$ style $p$ _ { $i$ , j } = p $_$ { $j$ , $i,j\in [1,n]:i\neq j$ $p_{i,j}=p_{j,i}$ } 、 $i,j\in [1,n]:i\neq j$ [ $1$ , n $i,j\in [1,n]:i\neq j$ : $i,j\in [1,n]:i\neq j$ $i,j\in [1,n]:i\neq j$ $i,j\in [1,n]:i\neq j$ \ $display style$ i , $j$ \ $in [$ 1, $n$ ] : $i$ \ $neq$ j }
$p_{i,i}\leq p_{i,k}+p_{k,j}$ $i,j,k\in [1,n]:i\neq j\neq k$ i $p_{i,i}\leq p_{i,k}+p_{k,j}$ $p_{i,i}\leq p_{i,k}+p_{k,j}$ $i,j,k\in [1,n]:i\neq j\neq k$ $p_{i,i}\leq p_{i,k}+p_{k,j}$ $i,j,k\in [1,n]:i\neq j\neq k$ $p_{i,i}\leq p_{i,k}+p_{k,j}$ + $p_{i,i}\leq p_{i,k}+p_{k,j}$ $p_{i,i}\leq p_{i,k}+p_{k,j}$ { $i,j,k\in [1,n]:i\neq j\neq k$ $p_{i,i}\leq$ $p_{i,k}+p_{k,j}:$ i $i,j,k\in [1,n]:i\neq j\neq k$ k $($ 모든 $i,j,k\in [1,n]:i\neq j\neq k$ i,j, $i,j,k\in [1,n]:i\neq j\neq k$ [ 1 , $n$ ]): $i,j,k\in [1,n]:i\neq j\neq k$ j $i,j,k\in [1,n]:i\neq j\neq k$ k (i $,j,j,n)$ : $i$ k k \ $displaystyleq$ \ $neq$ \ neq \ $neq$ \ $neq$ k $i,j,k\in [1,n]:i\neq j\neq k$ }
$\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ $i\in [1,n]$ $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ $i\in [1,n]$ $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ / $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ p $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ , $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ = $1$ / $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ \ $displaystyle$ $\$ $sum$ _ { j $\sum _{j=1}^{n}1/2^{p_{i,j}}=1/2$ = $1 }^{$ p _ { i , $j}$ = 1 $/2$ $i\in [1,n]$ [ $i\in [1,n]$ , $n$ ] $i\in [1,n]$ (이것은 Kraft - Mc Millan 부등식의 변형)
$\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ i $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ = $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ n $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ ∑ $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ = 1 $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ p $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ , $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ / $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ i , j $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ = $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ n $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ - 3 { $displaystyle$ \ $sum _$ { i $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ = { i = $1 } p _$ { i , j } / $2$ ^{ $p _$ { $i$ , j } = 2 $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ - $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ 3 $\sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3$ ^[7] $。$

이러한 동등성은 경로 길이 ^[7]수집이 n개의 리프로 UBT를 인코딩하기 위해 필요하고 독립적인 것으로 증명되었습니다.그것들도 충분한지는 현재 알려져 있지 않다.

대체 이름

뿌리가 없는 이진수는 자유 이진수,^[8] 입방수,^[9] 삼원수^[5],^[10] 삼원수로도 불린다.그러나 "자유 이진 트리"라는 이름은 2단계 노드를^[11] 가질 수 있는 루트 트리 및 순서 없는 하위 ^[12]노드를 가진 루트 이진 트리에도 적용되었으며, "삼원 트리"라는 이름은 노드당 하위 노드가 3개인 루트 트리를 의미하기 위해 더 자주 사용됩니다.

메모들

^ ^a ^b ^c 퍼나스(1984년).
^ 예를 들어,Eppstein(2009)은 클러스터와 트리 간에 동일한 대응관계를 가지지만 루트되지 않은 트리 대신 루트 이진 트리를 사용하여 루트 노드의 임의 선택을 포함한다.
^ Hendy & Penny (1989)
^ 세인트 존 외 (2003년).
^ ^a ^b Robertson & Seymour (1991)
^ 제모, 비숍 & 캐닝(2007)
^ ^a ^b ^c ^d Catanzaro D, Pesenti R, Wolsey L (2020). "On the Balanced Minimum Evolution Polytope". Discrete Optimization. 36: 100570. doi:10.1016/j.disopt.2020.100570. S2CID 213389485.
^ Czumaj & Gibbons (1996)
^ 엑수(1996년).
^ Cilibrasi & Vitanyi (2006년).
^ Harary, Palmer & Robinson(1992)
^ Przyticka & Larmore(1994년).

레퍼런스

를 클릭합니다Balding, D. J.; Bishop, Martin J.; Cannings, Christopher (2007), Handbook of Statistical Genetics, vol. 1 (3rd ed.), Wiley-Interscience, p. 502, ISBN 978-0-470-05830-5.
를 클릭합니다Cilibrasi, Rudi; Vitanyi, Paul M.B. (2006). "A new quartet tree heuristic for hierarchical clustering". arXiv:cs/0606048..
를 클릭합니다Czumaj, Artur; Gibbons, Alan (1996), "Guthrie's problem: new equivalences and rapid reductions", Theoretical Computer Science, 154 (1): 3–22, doi:10.1016/0304-3975(95)00126-3.
를 클릭합니다Eppstein, David (2009), "Squarepants in a tree: Sum of subtree clustering and hyperbolic pants decomposition", ACM Transactions on Algorithms, 5 (3): 1–24, arXiv:cs.CG/0604034, doi:10.1145/1541885.1541890, S2CID 2434.
를 클릭합니다Exoo, Geoffrey (1996), "A simple method for constructing small cubic graphs of girths 14, 15, and 16" (PDF), Electronic Journal of Combinatorics, 3 (1): R30, doi:10.37236/1254.
를 클릭합니다Furnas, George W. (1984), "The generation of random, binary unordered trees", Journal of Classification, 1 (1): 187–233, doi:10.1007/BF01890123, S2CID 121121529.
를 클릭합니다Harary, Frank; Palmer, E.M.; Robinson, R.W. (1992), "Counting free binary trees admitting a given height" (PDF), Journal of Combinatorics, Information, and System Sciences, 17: 175–181.
Hendy, Michael D.; Penny, David (1989), "A framework for the quantitative study of evolutionary trees", Systematic Biology, 38 (4): 297–309, doi:10.2307/2992396, JSTOR 2992396
를 클릭합니다Przytycka, Teresa M.; Larmore, Lawrence L. (1994), "The optimal alphabetic tree problem revisited", Proc. 21st International Colloquium on Automata, Languages and Programming (ICALP '94), Lecture Notes in Computer Science, vol. 820, Springer-Verlag, pp. 251–262, doi:10.1007/3-540-58201-0_73.
를 클릭합니다Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory, 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N.
를 클릭합니다St. John, Katherine; Warnow, Tandy; Moret, Bernard M. E.; Vawterd, Lisa (2003), "Performance study of phylogenetic methods: (unweighted) quartet methods and neighbor-joining" (PDF), Journal of Algorithms, 48 (1): 173–193, doi:10.1016/S0196-6774(03)00049-X, S2CID 5550338.

[f84-1] 퍼나스(1984년).

[2] 예를 들어,Eppstein(2009)은 클러스터와 트리 간에 동일한 대응관계를 가지지만 루트되지 않은 트리 대신 루트 이진 트리를 사용하여 루트 노드의 임의 선택을 포함한다.

[3] Hendy & Penny (1989)

[4] 세인트 존 외 (2003년).

[rs91-5] Robertson & Seymour (1991)

[6] 제모, 비숍 & 캐닝(2007)

[On_the_Balanced_Minimum_Evolution_P-7] Catanzaro D, Pesenti R, Wolsey L (2020). "On the Balanced Minimum Evolution Polytope". Discrete Optimization. 36: 100570. doi:10.1016/j.disopt.2020.100570. S2CID 213389485.

[8] Czumaj & Gibbons (1996)

[9] 엑수(1996년).

[10] Cilibrasi & Vitanyi (2006년).

[11] Harary, Palmer & Robinson(1992)

[12] Przyticka & Larmore(1994년).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Search

루트가 없는 이진 트리

네임스페이스

더

목차

정의들

관련 구조

루트 바이너리 트리

계층 클러스터링

진화목

분기 분해

열거

기본적인 동등성

대체 이름

메모들

레퍼런스