제타 포텐셜

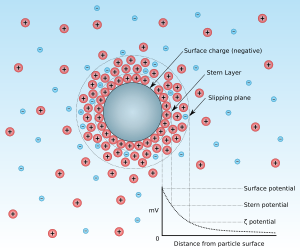
Zeta potential
분산 매체에 매달린 입자의 충전 표면으로부터의 거리 함수로써 이온 농도와 전위차를 나타낸 도표

제타 전위는 미끄러지는 평면에서 전기 전위다. 이 평면은 표면에 부착된 유체와 이동 유체를 분리하는 인터페이스다.

제타 포텐셜은 콜로이드 분산의 전기유전성을[1][2] 과학적으로 일컫는 말이다. 콜로이드 화학 문헌에서는 보통 그리스 문자 제타(zeta)를 사용하여 표기되는데, 따라서 ζ-potential을 사용한다. 일반적인 단위는 볼트(V) 또는 더 일반적으로 밀리볼트(mV)이다. 이론적 관점에서 제타 전위는 인터페이스에서 멀리 떨어진 벌크 유체의 한 점에 상대적인 미끄러짐 평면의 위치에 있는 계면 이중층(DL)의 전기 전위다. 즉, 제타 전위는 분산된 입자에 부착된 유체의 산란 매체와 정지층 사이의 전위차이다.

제타 전위는 미끄러지는 평면에 의해 경계된 지역 내에 포함된 순전하로 인해 발생하며, 또한 해당 평면의 위치에 따라 달라진다. 따라서 충전량의 크기를 정량화하는 데 널리 사용된다. 그러나 제타 전위는 다른 위치에서 정의되기 때문에 이중 층의 스턴 전위 또는 전기 표면 전위와 같지 않다.[3][4][5][6] 그러한 평등의 가정은 신중하게 적용되어야 한다. 그럼에도 불구하고, 제타 전위는 종종 이중 레이어 특성의 특성화를 위해 이용 가능한 유일한 경로다.

제타 전위는 콜로이드 분산의 안정성을 나타내는 중요하고 쉽게 측정할 수 있는 지표다. 제타 전위의 크기는 산포에서 유사하게 전하된 인접 입자 사이의 정전기 반발 정도를 나타낸다. 충분히 작은 분자와 입자의 경우, 높은 제타 전위는 안정성을 부여할 것이다. 즉, 용액이나 분산은 집계에 저항할 것이다. 잠재력이 작을 때, 매력적인 힘은 이 거부감을 초과할 수 있고 분산은 부서지고 휘어질 수 있다. 그래서 제타 전위(음 또는 양)가 높은 콜로이드들은 전기적으로 안정되는 반면 제타 전위성이 낮은 콜로이드들은 표에 요약된 것처럼 응고되거나 점착되는 경향이 있다.[7]

제타 전위에[8] 따른 콜로이드의 안정성 거동
제타 전위(mV) 안정성 거동작
0에서 ±5까지 급속 응고 또는 응고
±10 ~ ±30 초기 불안정
±30 ~ ±40 적당한 안정성
±40 ~ ±60 좋은 안정성
>61 탁월한 안정성

측정

제타 전위를 측정할 수 있는 몇 가지 새로운 계측 기법이 존재한다. 제타 전위 분석기는 고체, 섬유 또는 분말 물질을 측정할 수 있다. 인터네션에서 발견된 모터는 샘플을 통해 전해질 용액의 진동 흐름을 생성한다. 인터섹션의 여러 센서는 다른 요소들을 모니터하기 때문에 첨부된 소프트웨어는 제타 전위를 찾기 위한 계산을 할 수 있다. 온도, pH, 전도도, 압력, 스트리밍 전위는 모두 이 때문에 인터네이트에서 측정된다.

제타 전위는 이론적 모델과 실험적으로 결정된 전기적 이동성 또는 동적 전기적 이동성을 사용하여 계산할 수도 있다.

전기 운동 현상과 전기 음향 현상은 제타 전위 계산에 사용되는 일반적인 데이터 출처다. (제타 전위적 적정화 참조)

전기 운동 현상

주요 기사: 전기 운동 현상

전기영동체는 입자의 제타전위를 추정하는데 사용되는 반면 스트리밍 전위/전류가 다공성 몸체와 평평한 표면에 사용된다. 실제로 산포의 제타 전위는 산포에 전기장을 적용하여 측정한다. 제타 전위를 가진 분산 내의 입자는 제타 전위의 크기에 비례하는 속도로 반대 전하의 전극을 향해 이동한다.

이 속도는 레이저 도플러 풍속계의 기법을 사용하여 측정한다. 이러한 움직이는 입자에 의해 발생하는 입사 레이저 빔의 주파수 이동이나 위상 변화는 입자 이동성으로 측정되며, 이 이동성은 분산 점도와 유전적 허용률, 그리고 스몰루코프스키 이론을 적용하여 제타 전위로 변환된다.[9]

전기영양증

주요 기사: 전기영양증

전기적 이동성은 측정 가능한 변수인 전기적 이동 속도에 비례한다. 전기적 이동성과 제타 잠재력을 연결시키는 몇 가지 이론이 있다. 그것들은 전기영양에 관한 기사와 콜로이드와 인터페이스 과학에 관한 많은 책에 간략하게 설명되어 있다. [3][4][5][10] 전기동학 현상에 관한 세계 전문가 그룹이 작성한 IUPAC 기술 보고서가[11] 있다. 기계의 관점에서 보면, 세 가지 다른 실험 기법이 있다: 미세 전자파, 전기적 빛의 산란, 그리고 튜닝 가능한 저항성 펄스 감지. 미세전극은 움직이는 입자의 이미지를 만들어 내는 장점이 있다. 반면 시료세포의 벽면에서의 전기오스로 인해 복잡하다. 전기생광 산란은 동적 빛의 산란을 기반으로 한다. 모세혈관 세포의 경우를 제외하고 전기-오토믹 흐름의 문제를 제거하는 열린 세포에서의 측정이 가능하다. 그리고, 그것은 매우 작은 입자들을 특징 짓는데 사용될 수 있지만, 움직이는 입자들의 이미지를 표시하는 능력을 잃어버린 가격에 사용될 수 있다. TRPS(Tunable Ristance Pulse Sensing, TRPS)는 저항 펄스 신호의 지속시간을 기준으로 개별 입자의 제타 전위를 측정하는 임피던스 기반 측정 기법이다.[12] 나노입자의 변환 지속시간은 전압과 인가압력의 함수로 측정된다. 역변환 시간 대 전압 의존성 전기 이동성으로부터, 따라서 제타 전위가 계산된다. TRPS 방법의 주요 장점은 입자별 크기 및 표면 전하 측정을 동시에 허용하여 광범위한 합성 및 생물학적 나노/미크로파티클과 혼합물 분석을 가능하게 한다는 것이다.[13]

이러한 모든 측정 기법에는 표본의 희석이 필요할 수 있다. 때때로 이 희석은 표본의 속성과 제타 전위 변화에 영향을 미칠 수 있다. 평형 상등액을 사용하여 희석하는 데는 정당화된 한 가지 방법만이 있다. 이 경우 표면과 벌크 액체 사이의 계면 평형이 유지되고 제타 전위는 서스펜션에 있는 입자의 모든 부피 분율에서 동일할 것이다. 희석제가 알려진 경우(화학 제형의 경우처럼) 추가 희석제를 준비할 수 있다. 희석액을 알 수 없는 경우에는 원심분리하여 평형 상등액을 쉽게 얻을 수 있다.

전기음향현상

주요 기사: 전기음향현상

제타 전위 특성화에 널리 사용되는 전기음향 효과는 콜로이드 진동 전류와 전기음향 진폭 두 가지가 있다.[5] 이러한 효과를 이용하여 제타 잠재력에 의존하는 동적 전기적 이동성을 측정하는 상업적으로 이용 가능한 계측기가 있다.

전기음향 기법은 희석 없이 온전한 시료에서 측정을 수행할 수 있는 장점이 있다. 출판되고 검증이 잘 된 이론은 부피 분율에서 최대 50%까지 그러한 측정을 허용한다. 동적 전기영동성 이동성에서 제타 전위를 계산하려면 입자와 액체의 밀도에 대한 정보가 필요하다. 또한, 약 300 nm를 초과하는 큰 입자의 경우 필요한 입자 크기에 대한 정보도 제공된다.[citation needed]

계산

실험 데이터로부터 제타 잠재력을 계산하기 위해 가장 잘 알려져 있고 널리 사용되는 이론은 마리안 스몰루코프스키가 1903년에 개발한 이론이다.[14] 이 이론은 원래 전기영양증을 위해 개발되었지만, 지금은 전기음향학의 확장도 이용할 수 있다.[5] 스몰루코프스키의 이론은 어떤 형태나 농도의 분산된 입자에 유효하기 때문에 강력하다. 그러나 다음과 같은 한계가 있다.

  • 상세한 이론적 분석은 스몰루코프스키의 이론이 충분히 얇은 이중층에만 유효하다는 것을 증명했는데, 데비예 길이 / 1이 입자 반지름보다 훨씬 작을 때,
"씬한 이중층"의 모델은 전기영동 이론뿐만 아니라 다른 많은 전기영동학 및 전기음향 이론에도 엄청난 단순화를 제공한다. 이 모델은 대부분의 수성 시스템에 유효하다. 왜냐하면 데비 길이는 일반적으로 물에서 몇 나노미터밖에 되지 않기 때문이다. 이 모델은 순수한 물의 이온 강도에 접근하는 용액의 나노콜로이드에 대해서만 파손된다.
  • 스몰루코프스키의 이론은 표면 전도성의 기여를 무시한다. 이것은 현대 이론에서 작은 두힌 수의 조건으로 표현된다.

유효성의 범위가 넓은 전기공학과 전기음향 이론의 발전은 20세기 동안 많은 연구의 목적이었다. 표면 전도성을 통합하고 전기동작과 전기음향 응용 모두에 대해 작은 두힌 수의 제약을 없앤 몇 가지 분석 이론이 있다.

그 방향으로의 초기 개척 작업은 오버벡과[15] 부스로 거슬러 올라간다.[16]

어떤 제타 잠재력에도 유효한 현대적이고 엄격한 전기 운동학 이론들, 그리고 종종 모든 주로 소련계 우크라이나어(덕힌, 샤일로프 등)와 오스트레일리아어(오브리엔, 화이트, 헌터 등) 학교에서 유래한다. 역사적으로 첫 번째는 덕힌-세메니킨 이론이었다.[17] 비슷한 이론이 10년 후 오브라이언과 헌터에 의해 만들어졌다.[18] 얇은 이중 층을 가정하면, 이러한 이론들은 오브라이언과 화이트가 제공하는 수치적 해법에 매우 가까운 결과를 산출할 것이다.[19] 데비예 길이와 두힌 수의 어떤 값에도 유효한 일반적인 전기음향 이론도 있다.[5][10]

헨리의 방정식

'헨리 방정식'은 여기서 방향을 바꾼다. 가스법은 헨리의 법칙을 보라.

κa가 단순한 해석 모델을 이용할 수 있는 큰 값과 숫자 계산이 유효한 낮은 값 사이에 있을 때, 제타 전위가 낮을 때 헨리의 방정식을 사용할 수 있다. For a nonconducting sphere, Henry's equation is , where f1 is the Henry function, one of a collection of functions which vary smoothly from 1.0 to 1.5 as κa approaches infinity.[20]

참조

  1. ^ IUPAC, 화학용어 종합편찬, 제2편. ("금책")(1997년). 온라인 수정 버전: (2006–) "전동적 잠재력, ζ". doi:10.1351/골드북.E01968
  2. ^ ISO 국제 표준 13099, 파트 1,2,3, "Colloidal 시스템 – Zeta 잠재적 결정을 위한 방법", (2012)
  3. ^ a b Lyklema, J. "인터페이스와 콜로이드 사이언스의 재무", vol.2, 페이지.3.208, 1995 ISBN0-12-460529-X
  4. ^ a b 러셀, W.B., 사빌, D.A. 및 W.R. "콜로이달 디스패션", 캠브리지 대학 출판부, 1992 ISBN 0-521-42600-6[page needed]
  5. ^ a b c d e A. S.와 괴츠, P. J. 초음파, 엘스비어, 2017 ISBN 978-0-444-63908-0을[page needed] 이용한 액체, 나노 및 미세 입자 및 다공성 신체의 특성
  6. ^ Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices. Cambridge University Press. ISBN 978-0-521-11903-0.[페이지 필요]
  7. ^ Hanaor, D.A.H.; Michelazzi, M.; Leonelli, C.; Sorrell, C.C. (2012). "The effects of carboxylic acids on the aqueous dispersion and electrophoretic deposition of ZrO2". Journal of the European Ceramic Society. 32 (1): 235–244. arXiv:1303.2754. doi:10.1016/j.jeurceramsoc.2011.08.015. S2CID 98812224.
  8. ^ Kumar, Ajeet; Dixit, Chandra Kumar (2017). "Methods for characterization of nanoparticles". Advances in Nanomedicine for the Delivery of Therapeutic Nucleic Acids. pp. 43–58. doi:10.1016/B978-0-08-100557-6.00003-1. ISBN 9780081005576.
  9. ^ 레이저 도플러 전기영동체를 이용한 제타 잠재력 - Malvern.com
  10. ^ a b 헌터, R.J. "콜로이드 사이언스 창립", 옥스퍼드 대학 출판부, 1989 ISBN 0-19-855189-4[page needed]
  11. ^ Delgado, A. V.; González-Caballero, F.; Hunter, R. J.; Koopal, L. K.; Lyklema, J. (1 January 2005). "Measurement and Interpretation of Electrokinetic Phenomena (IUPAC Technical Report)". Pure and Applied Chemistry. 77 (10): 1753–1805. doi:10.1351/pac200577101753. hdl:10481/29099. S2CID 16513957.
  12. ^ "Zeta Potential Measurement With TRPS". Izon Science.
  13. ^ Vogel, Robert; Pal, Anoop K.; Jambhrunkar, Siddharth; Patel, Pragnesh; Thakur, Sachin S.; Reátegui, Eduardo; Parekh, Harendra S.; Saá, Paula; Stassinopoulos, Adonis; Broom, Murray F. (12 December 2017). "High-Resolution Single Particle Zeta Potential Characterisation of Biological Nanoparticles using Tunable Resistive Pulse Sensing". Scientific Reports. 7 (1): 17479. Bibcode:2017NatSR...717479V. doi:10.1038/s41598-017-14981-x. PMC 5727177. PMID 29234015.
  14. ^ Smoluchowski, Maryan (1903). "Przyczynek do teoryi endosm ozy elektrycznej i kilku zjawisk pokrewnych" [Contribution to the theory of electro-osmosis and related phenomena] (PDF) (in Polish). Archived from the original (PDF) on August 10, 2017.
  15. ^ Overbeek, J.Th.G (1943). "Theory of electrophoresis — The relaxation effect". Koll. Bith.: 287.
  16. ^ Booth, F. (1948). "Theory of Electrokinetic Effects". Nature. 161 (4081): 83–6. Bibcode:1948Natur.161...83B. doi:10.1038/161083a0. PMID 18898334.
  17. ^ 두힌, S.S., 세메니킨, N.M. 콜. Zhur, 32, 366 (1970)
  18. ^ O'Brien, Richard Wyndham; Hunter, Robert John (July 1981). "The electrophoretic mobility of large colloidal particles". Canadian Journal of Chemistry. 59 (13): 1878–1887. doi:10.1139/v81-280.
  19. ^ O'Brien, Richard W.; White, Lee R. (1978). "Electrophoretic mobility of a spherical colloidal particle". Journal of the Chemical Society, Faraday Transactions 2. 74: 1607. doi:10.1039/F29787401607.
  20. ^ Delgado, A. V.; González-Caballero, F.; Hunter, R. J.; Koopal, L. K.; Lyklema, J. (2005-01-01). "Measurement and Interpretation of Electrokinetic Phenomena (IUPAC Technical Report)". Pure and Applied Chemistry. 77 (10): 1753–1805. doi:10.1351/pac200577101753. hdl:10481/29099. ISSN 1365-3075. S2CID 16513957.