접근성 관계
Accessibility relation접근성 관계는 모달 논리에 대한 관계 의미론에서 문장에 진실 값을 할당하는 데 핵심적인 역할을 하는 관계다. 관계 의미론에서, 가능한 에서의 모달 공식의 진리 값은 다른 가능한 v{\에서 진실인지에 따라 달라질 수 있지만, 관계 R이(가) v v과(: P displaystystytyle 에 연관되어 있는 경우에만 해당된다.은(는) v 에서 유지되며 P {\ \ P은(는 w {\에서 참이 된다 의 사실이 중요하다. 이(가) w과와) 관련이 없는 경우 P P이(가) 과(와) 같은 다른w {\에서 열리지 않는 한 u w에서 거짓이(가 될 것이다[1][2]
접근성 관계는 자연어 모달 문장이 일부에 의존하지만 모든 대안 시나리오에 의존하지는 않는다는 사실에 의해 개념적으로 동기가 부여된다. 예를 들어 '비가 올지도 모른다'는 문장은 단순히 비가 내렸던 시나리오를 상상할 수 있다는 이유만으로 일반적으로 사실이라고 판단되지 않는다. 오히려 그 진실은 그러한 시나리오가 이용 가능한 정보에 의해 배제되는지 여부에 달려 있다. 사실은 w 이(가) 의 발표자가 사용할 수 있는 정보와 호환되는 경우 와 같은 접근성 관계를 선택하여 모달 논리로 공식화할 수 있다
이 아이디어는 모달 로직의 다른 적용으로 확장될 수 있다. In epistemology, one can use an epistemic notion of accessibility where for an individual iff does not know something which would rule out the hypothesis that . In deontic modal logic, one can say that iff 는 의 도덕적 기준을 고려할 때 도덕적으로 이상적인 세계다 컴퓨터 과학에 모달 논리를 적용하면 소위 가능한 세계를 가능한 상태를 나타내는 것으로 이해할 수 있고 접근성 관계를 하나의 프로그램으로 이해할 수 있다. 그런 다음 을 실행하면 컴퓨터를 상태 에서 v 으)로 전환할 수 있는 경우 w
모달 로직의 다른 적용은 허용 가능한 접근성 관계에 대한 다른 제한을 제안할 수 있으며, 이는 결국 다른 유효성을 야기할 수 있다. 타당성이 접근성 관계의 조건과 어떻게 연관되어 있는지에 대한 수학적인 연구는 모달 대응 이론으로 알려져 있다.
참고 항목
참조
- ^ Blackburn, Patrick; de Rijke, Maarten; Venema, Yde (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science.
- ^ van Benthem, Johan (2010). Modal Logic for Open Minds (PDF). CSLI. S2CID 62162288. Archived from the original (PDF) on 2020-02-19.
- Gerla, G.; 첫 번째 순서 논리를 위한 변환 의미론, Logique et Analyze, No. 117–118, 페이지 69–79, 1987.
- Fitelson, Brandon; "Accessibility" 및 Modality, 2003에 대한 Notes.
- 브라운, 커티스; 프로포지셔널 모달 논리: 몇 가지 첫걸음, 2002.
- 1980년 옥스포드의 크립케, 사울; 명명과 필요.
- Lewis, David K. (1968). "Counterpart Theory and Quantified Modal Logic". The Journal of Philosophy. 65 (5): 113–126. doi:10.2307/2024555. JSTOR 2024555.
- Gasquet, Olivier; et al. (2013). Kripke's Worlds: An Introduction to Modal Logics via Tableaux. Springer. pp. 14–16. ISBN 978-3764385033. Retrieved 23 July 2020.
- 로직 시스템 목록에는 가장 인기 있는 모달 로직 목록이 나열되어 있다.
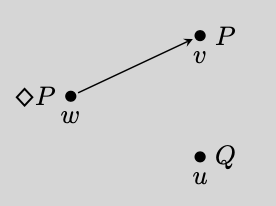


 (가) 참이라는 사실이
(가) 참이라는 사실이










