능동 및 수동 변환

기하학적 변환은 두 가지 유형으로 구분될 수 있습니다: 고정된 참조 프레임 또는 좌표계에 상대적인 점 집합의 물리적 위치를 변경하는 능동적 또는 알리바이 변환(allibi는 "동시에 다른 곳에 있음"을 의미함)과 점을 고정시켜 놓지만 프레임을 변경하는 수동적 또는 별칭 변환 o.해당 시스템이 설명되는 좌표계에 대한 선호도(alias는 "다른 이름으로 이동"됨을 의미함).변환에 의해, 수학자들은 보통 능동적인 변환을 언급하는 반면, 물리학자와 공학자들은 둘 중 하나를 의미할 수 있습니다.^{[citation needed]}

예를 들어, 능동 변환은 강체의 연속적인 위치를 설명하는 데 유용합니다.한편, 수동 변환은 대퇴골에 대한 경골의 움직임, 즉 바닥에 고정된 (전체) 좌표계가 아니라 대퇴골과 함께 움직이는 (국소) 좌표계에 대한 움직임을 관찰하기 위한 인간의 움직임 분석에서 유용할 수 있습니다.^[2]

3차원 유클리드 공간에서, 능동적이든 수동적이든 적절한 강성 변환은 나사 변위, 축을 따른 변환의 구성, 그리고 그 축에 대한 회전으로 나타낼 수 있습니다.

능동 변환과 수동 변환이라는 용어는 특수 상대성 이론에서 로렌츠 변환을 설명하기 위해 1957년 발렌타인 바그만에 의해 처음 소개되었습니다.^[3]

예

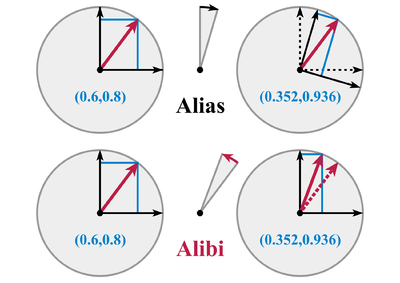
예를 들어, 벡터 $v$ =${\displaystyle }$( v ${\displaystyle 1_{}}$ ${\displaystyle v_{}}$ ${\displaystyle {}_{}}$ )${\displaystyle {}_{}}$∈ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle \mathbf {v}$ = ($v_{1}, v_{2})\in \mathbb {R}^{2}$에서 평면의 벡터라고 하자$.$반시계 방향으로 각도 θ을 통과하는 벡터의 회전 행렬은 다음과 같습니다.

아래에 설명된 바와 같이 능동 변환 또는 수동 변환으로 볼 수 있습니다(위 행렬은 반전됩니다).

유클리드 공간 R의³ 공간 변환

일반적으로 공간 변환 $T$ :${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ → ${\displaystyle {}^{}}$ 3 ${\displaystyle T\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$는 변환과 선형 변환으로 구성될 수 있습니다.다음에서는 변환이 생략되고 선형 변환은 3×3 행렬 T ${\displaystyle T}$로 표시됩니다$.$

능동변환

$활성$ 변환으로$$T {\$displaystyle$T}은(는) 초기 벡터 $v$ = ${\displaystyle ({}_{}}$ ${\displaystyle x_{}}$ ${\displaystyle v_{}}$ v ${\displaystyle z_{}}$ ${\displaystyle \mathbf {v}$ = ($v_{x}, v_{y},$ ${\displaystyle {v\_}_{}^{}}$${z})}$을(는) 새로운 벡터 $v{\displaystyle {}^{}}$ = ${\displaystyle ({}_{}^{}}$ ${\displaystyle x_{}^{}}$ ${\displaystyle \text{'},}$ ${\displaystyle v_{}^{}}$ v ${\displaystyle \text{'},}$ ${\displaystyle {}_{}^{}}$ z${\displaystyle {}_{}^{}\text{'}){}_{}}$= ${\displaystyle T}$ (${\displaystyle v_{}}$ ${\displaystyle x_{}}$ v${\displaystyle {}_{}}$ ${\displaystyle v_{}}$z ) {\$displaystyle$ \$mathbf$ {v$}$'= $(v'_{x$},$v'_{y},v'_{z})$$=T\mathbf {v} =T(v_{x},v_{y},v_{z$

$\{{\displaystyle {}_{}^{}}$ '${\displaystyle {}_{}^{}}$= ${\displaystyle T}$ ${\displaystyle (1,}$ 0${\displaystyle ,}$ ${\displaystyle 0}$ ${\displaystyle ),{}_{}^{}}$= T ${\displaystyle (0,}$ ${\displaystyle 1,}$ 0 ${\displaystyle ),{}_{}^{}}$ = T (${\displaystyle 0,}$ ${\displaystyle 0}$,${\displaystyle 1}$ )${\displaystyle }$}${\displaystyle \{\mathbf$ {$e}$'_${x}$= T($1, 0, 0),\\mathbf {e}$ '$_{y$} =$T(0, 1,$ 0$),\mathbf {e} '_{z$} = $T(0, 0, 1)\}$를 새 기저로 본다면,그러면 새 기저에서 새로운 벡터 $v$ ${\displaystyle {}^{}}$ = v ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ v ${\displaystyle {}_{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle \mathbf {v}$ '=$v_{x}\mathbf {e} '_{x}$ + $v_{y}\mathbf {e} '_{y}$ + $v_{z}\mathbf {e} '_{z}'$의 좌표는 $v$ = v ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$+ ${\displaystyle v_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ {$v}$=$v_{x}\mathbf {e} _{x}$ + $v_{y}\mathbf {e} _{y}$ + $v_{z} in$원초적 근거활성 변환은 다른 벡터 공간으로의 선형 변환으로도 의미가 있습니다.변환이 공간에서 자신으로 변환될 때에만 (위와 같이) 새로운 벡터를 비프림 기반으로 작성하는 것이 타당합니다.

수동변환

반면, $T$ ${\displaystyle T}$를 수동 변환으로 볼 때, 초기 벡터 $v$ = ${\displaystyle ({}_{}}$ ${\displaystyle x_{}}$ ${\displaystyle v_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle z_{}}$) ${\displaystyle {v}$ = ($v_{x},v_{y},v_{z}}$는 그대로 둔 채 좌표계와 그 기저 벡터가 반대 방향으로 변환되는 동안, 즉,${\displaystyle {\mathrm{역변환}}^{}}$ T${\displaystyle {}^{}}$- 1 ${\$ T$^\{-$^[4]$1}}.$그러면 기저 벡터가 있는 새로운 좌표계 XYZ가 나타납니다.

새 좌표계 XYZ에 대한$$ $v{\displaystyle \mathbf{}}$ ${\$의 새 좌표$({\displaystyle {vX}_{}}$ ${\displaystyle {vY}_{}}$ ${\displaystyle {vZ}_{}}$ ${\displaystyle(v_{X},v_{Y},v_{Z})$는 다음과 같이 제공됩니다.

이 방정식으로부터 새로운 좌표는 다음과 같이 주어집니다.

수동 변환 $T{\displaystyle }$ ${\displaystyle T}$는 이전 좌표를 새 좌표로 변환합니다$$.

두 종류의 변환 사이의 동등성에 주목하십시오: 능동 변환에서 새로운 점의 좌표와 수동 변환에서 점의 새로운 좌표는 같습니다. 즉,

추상 벡터 공간에서

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2023년 9월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

능동 변환과 수동 변환의 구별은 추상 벡터 공간을 고려함으로써 수학적으로 알 수 있습니다.

$유한$ $차원$벡터 공간 V {\$displaystyle$ $V$$}를$K 필드 {\$displaystyle$ $}(R$ {\$displaystyle \mathbb$ {$} 또는$ C {\$displaystyle$ \mathbb ${C})$ 위에 고정하고 기저 $B$ =${\displaystyle }${${\displaystyle e_{}}$ i}${\displaystyle {}_{}{1}_{}}$ ${\displaystyle {\le }_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {\le }_{}}$ n ${\displaystyle$ {$B}$= {$e_{i}\}_{1\leq i\leq n}$의 V {\$displaystyle V}$ 위에 고정합니다$.$이 기저는 동형 $C{\displaystyle :}$ ${\displaystyle {Kn}^{}}$ → ${\displaystyle V}$ ${\displaystyle C:$$성분$ 맵(${vi}_{}$ $1_{}{\le }_{}$ $i_{}$ ${\le }_{}$ $n_{}$ $=$ $({v1}_{}$,$$$⋯$$,$ ${vn}_{}$ )${}_{}$$↦ ∑$ ${ivi}_{}$ ${\textstyle$ i$\leq$n}$=$($v_{1},\cdots,v_{n})\maps to \sum$ _${i}v_{i}$v_${i}.$

그러면 활성 변환은 $V{\displaystyle }$ ${\displaystyle V}$의 내형태 즉$,$ $V{\displaystyle }$ ${\displaystyle V}$에서 자신으로의$$ 선형 맵입니다.이러한 변환 τ ∈ ${\displaystyle \text{End}}$ (${\displaystyle V)}$ ${\displaystyle \tau \in {\text{End}}(V)}$을$($를) 사용하면 벡터 $v$ ∈ ${\displaystyle V}$ ${\displaystyle v\in V}$가 $v$ ↦ τ v ${\displaystyle v\mapsto$ \tauv$}로 변환$됩니다$.$기본 $B$ ${\displaystyle {\mathcal {B}}$에 대한 τ ${\displaystyle$\tau }의 구성 요소는 방정식 e $i_{}$ = ∑ j τ $j_{}$ $j_{}$ ${\textstyle$\tau $e_{i$}=\$sum$_${j}\$tau _${j}}를 통해$ 정의됩니다$.$그런 다음 $v$ ${\displaystyle v}$의 구성 요소가 ${\displaystyle {vi}_{}}$ ↦ τ ${\displaystyle {\mathrm{ij}}_{}}$ ${\displaystyle {vj}_{}}$ ${\displaystyle v_{i}\maps$ to $\tau _{ij}v_{j}}$로 변환됩니다$.$

수동 변환은 대신 $Kn {\$ K$^{n}}$의 내형입니다$.$${\displaystyle {vi}_{}}$ ↦ ${\displaystyle {\mathrm{Tij}}_{}}$ v ${\displaystyle j_{}}$ =${\displaystyle :}$ $'$ {\$displaystyle v_${i$}\mapsto T_{ij}v_{j$}=:$v'_{i$ 구성 요소에 적용됩니다. T {\$displaystyle T}$가 반전 가능하다면, 새로운 기저 $B{\displaystyle {}^{}}$' = ${\displaystyle \{{}_{}^{}}$ ${\displaystyle i_{}^{}}$${\displaystyle {}_{}^{}}$ ${\displaystyle {\mathcal {$B}}'=\{$'$${i}\$$displaystyle v_{i}e_{i$}=$v'_{i}e_{i},$,${\displaystyle {}^{}}$로부터 ${\displaystyle {식}_{}^{}}$ e i${\displaystyle }$= (${\displaystyle {\mathrm{T}}^{}}$ - 1${\displaystyle {}^{}}$) ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\displaystyle e'_{i$}= ($T^{-1})_{ji}e_{j}}$를 유도할 수 있습니다.

${\displaystyle \text{끝}(V)}$ ${\displaystyle {\text{End}}(V)}$과 ${\displaystyle \text{끝}({Kn}^{}}$ ${\displaystyle {\text{End}}({K^{n}})}$ 공간이$$ 동형이지만 표준적으로 동형이 아닙니다.그럼에도 불구하고 기저 $B{\displaystyle \mathcal{}}$ ${\$를 선택하면 동형 사상을 구성할 수 있습니다$$.

좌/우 동작으로

종종 맵이 반전 가능한 경우로 제한하여 능동 변환은 변환의 일반$$ 선형 그룹 ${\displaystyle \text{GL}}$ ${\displaystyle (V)}$ ${\text{GL}(V)}$인 반면 수동 변환은 그룹 ${\displaystyle \text{GL}}$(${\displaystyle n,K)}$ ${\text$$GL}(n,K)}$입니다.

그러면 변환은 $V$ ${\displaystyle V}$의 밑면 공간에 작용하는 것으로 이해할 수 있습니다$.$ 능동 변환 τ ∈ ${\displaystyle \text{GL}}$ ${\displaystyle (V)}$ ${\displaystyle \tau \in {\text{GL}}(V)$는 밑면$${${\displaystyle {}_{}}$ ${\displaystyle i_{}}$}${\displaystyle {}_{}}$↦${\displaystyle }${τ ${\displaystyle e_{}}$ i}${\displaystyle \{e_{i}\}\map을 \{\tau e_{i}\}$에 보냅니다$.$ 한편 수동 변환 $T$ ∈ ${\displaystyle \text{GL}}$(${\displaystyle n,}$ ${\displaystyle K}$ )${\displaystyle }${\text${GL}}(n$) ${\displaystyle$T$\in {\text${GL})$,K)}$은(는) 기본$${${ei}_{}$ ${}_{}$ $↦$ $\{$$∑$ j$\underset{}{}{}^{}$- $1^{}$) ${}_{}$ $j_{}$ ${}_{}$ ${\textstyle \{e_{i}\}\map을 \left\{\sum _{j}(T^{-1})_{ji}e_{j}\right\}$로 보냅니다$.$

수동 변환의 역은 구성 $요소$가$$τ {\displaystyle $\tau}$$$및 T {\$displaystyle T}$에서 동일하게 변환되도록 보장합니다$.$ 그러면 능동 변환과 수동 변환 사이에 급격한 차이가 나타납니다. 능동 변환은 베이스에서 왼쪽에서 작용하는 반면 수동 변환은 반대로 인해 오른쪽에서 작용합니다.

$이$ 관찰은$$베이스 B {\$displaystyle {\mathcal${B}}를 동형 φ ${\displaystyle B_{}}$: ${\displaystyle V}$→ ${\displaystyle {Kn}^{}}$ {\$displaystyle$ \$Phi$_{\$mathcal$ {B$}}:$$V\$오른쪽 $화살표$ K$^{n$기저의 공간은 동치 동치 사상의 공간이며, ${\displaystyle \text{이소}}$(${\displaystyle V,}$ ${\displaystyle {Kn}^{}}$ ${\displaystyle {\text{$$Iso}}(V,K^{n}}.$${\displaystyle \text{GL}(V)}$ ${\displaystyle {\text{GL}(V)}$로 확인된 활성 변환은$$${\displaystyle \text{Iso}(V,{Kn}^{}}$ ${\displaystyle {\text{$왼쪽에서 합성으로 $Iso$$}}($V,$K^{n}}},$ ${\displaystyle \text{GL}(n,K)}${\$displaystyle {\text{GL}(n,K)}$가 Iso(${\displaystyle \text{V<img alt="{displaystyle {text{GL}}(n,K)}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/3eb25cb3093b56e4884bce03af9661e00a6c3901" style="vertical-align: -0.838ex; width:9.581ex; height:2.843ex;">}}$,${\displaystyle {Kn}^{}}$ ${\displaystyle {\text{$$ISO}}(V,K^{n})}$는 사전 구성에 의해 오른쪽에서$$ 시작됩니다.

그러면 베이스의 공간이 왼쪽 ${\displaystyle \text{GL}(V)}$ ${\text{GL}(V)$ -torsor$$ 및 오른쪽 ${\displaystyle \text{GL}(n,K)}$ ${\text{GL}(n,K)}$ -torsor로$$ 바뀝니다.

물리적 관점에서 능동적 변환은 물리적 공간의 변환으로, 수동적 변환은 물리적 공간의 설명에서 중복으로 특징지어질 수 있습니다.이것은 섬유에 오른쪽에서 작용하는 전이 지도에 의해 게이지 변환이 수학적으로 설명되는 수학적 게이지 이론에서 중요한 역할을 합니다.

참고 항목

• 기초변경
• 벡터의 공분산과 반변성
• 축의 회전
• 축의 병진

참고문헌

• Dirk Struik (1953) 분석적 기하학과 투영적 기하학 강의, 84페이지, Addison-Wesley

외부 링크

• UI 모호성