분리 이론의 생물학적 적용
Biological applications of bifurcation theory분리 이론의 생물학적 적용은 역동적인 시스템으로 모델링된 생물학적 네트워크의 행동을 이해하기 위한 프레임워크를 제공한다.생물학적 시스템의 맥락에서 분기 이론은 입력 매개변수의 작은 변화가 어떻게 시스템의 행동에 분기 또는 질적 변화를 일으킬 수 있는지를 설명한다.시스템 출력의 극적인 변화를 일으키는 능력은 유기체 기능에 필수적이며, 따라서 분기는 세포 주기의 스위치와 같은 생물학적 네트워크에서는 어디서나 볼 수 있다.null
생물학적 네트워크 및 동적 시스템
생물학적 네트워크는 진화에 기인하며 따라서 전기 네트워크와 같이 인간이 설계한 네트워크보다 표준화된 요소가 적고 잠재적으로 더 복잡한 상호작용을 가진다.세포 수준에서, 네트워크의 구성 요소들은 많은 종류의 단백질을 포함할 수 있는데, 그 중 다수는 유기체마다 다르다.네트워크 상호작용은 하나 이상의 단백질이 전사, 번역, 번역, 인산화 또는 다른 메커니즘을 통해 다른 단백질의 기능에 영향을 줄 때 발생한다.이러한 상호작용은 어떤 식으로든 표적 단백질의 작용을 활성화시키거나 억제한다.인간은 단순함과 질서에 대한 우려로 네트워크를 구축하는 반면, 생물학적 네트워크는 진화 과정에 걸쳐 중복성과 복잡성을 획득한다.따라서, 생물 네트워크의 양적 행동을 그 조직의 지식으로부터 예측하는 것은 불가능할 수 있다.마찬가지로, 동작이 특정 네트워크 모티브의 존재를 나타낼 수 있지만, 순수하게 그것의 행동에서 그것의 조직을 묘사하는 것은 불가능하다.null

그러나, 네트워크 상호작용에 대한 지식과 단백질과 단백질 상호작용에 대한 일련의 매개변수(보통 경험적 연구를 통해 얻음)로, 네트워크 모델을 역동적인 시스템으로 구성하는 것이 종종 가능하다.일반적으로 n개 단백질의 경우 동적계는 x가 일반적으로 단백질 농도인 다음과 같은 형태를[1] 취한다.
이러한 시스템들은 종종 해결하기가 매우 어렵기 때문에 선형 역학 시스템으로 네트워크를 모델링하는 것이 더 쉽다.선형 시스템은 xs 사이의 제품을 포함하지 않으며 항상 해결할 수 있다.그들은 모두 다음과 같은 양식을 가지고 있다.
불행히도 생물학적 시스템은 종종 비선형적이기 때문에 비선형 모델이 필요하다.null
입출력 모티브
생물학적 네트워크의 큰 잠재적 복잡성과 다양성에도 불구하고, 모든 1차적 네트워크 동작은 쌍곡선 또는 Michaelis-Menten, 극도로 민감하고, 바이스트 가능하며, 불가역적인 네 가지 입력-출력 모티브 중 하나로 일반화된다(부정적이고 따라서 생물학적으로 불가능한 입력)생산량이 많은 상태).생물학적 맥락에서 각각의 예는 각각의 페이지에서 찾을 수 있다.null
극도로 민감하고, 비스트할 수 있고, 불가역적으로 비스트할 수 있는 네트워크들은 모두 특정 매개변수 값에 대한 네트워크 동작의 질적 변화를 보여준다 – 이것들은 이들의 분기점이다.null
오류가 있는 경우 기본 분기점
비선형 동적 시스템은 일부 수량 x(예: 단백질 농도) 풍요의 변화가 그 자체에만 의존하는 1차원 예시 시스템으로 가장 쉽게 이해할 수 있다.
많은 기능이 어렵거나 불가능할 수 있는 시스템을 분석적으로 해결하는 대신 기하학적 접근으로 위상 초상화를 그리는 것이 가장 빠르고 유익한 경우가 많다.위상 초상화는 평형용액이나 고정점, 실제 선에 벡터장을 보여주는 미분방정식의 행동을 정성적으로 스케치한 것이다.null
분기점들은 고정점의 안정성 또는 존재의 변화를 시스템의 제어 매개변수로 설명한다.동적 시스템에서 분기에 대한 매우 간단한 설명으로 수직 빔 위에서 균형을 이룬 물체를 고려하십시오.물체의 질량은 제어 매개변수, r, 수직축으로부터의 빔의 편향은 동적 변수 x라고 생각할 수 있다. r이 증가함에 따라 x는 상대적으로 안정된 상태를 유지한다.그러나 질량이 특정 지점(분지점)에 도달하면 빔이 설정에서 사소한 결함에 의존하는 방향으로 갑자기 버클이 발생한다.이것은 피치포크 분리의 한 예다.제어 매개변수의 변경은 결국 시스템의 질적 동작을 변화시켰다.null
안장-노드 분리
보다 엄격한 예를 위해 다음 방정식으로 설명되는 그림 2에 표시된 동적 시스템을 고려하십시오.
여기서 r은 다시 제어 매개변수(그림 2에 ε 라벨로 표시됨)이다.시스템의 고정 지점은 위상 세로 곡선이 X축을 교차하는 위치로 표시된다.주어진 고정점의 안정성은 x축의 흐름 방향에 의해 결정될 수 있다. 예를 들어, 그림 2에서 녹색 지점은 불안정하며(전위적인 흐름), 빨간색 지점은 안정적이다(전위적인 흐름).처음에는 r이 0보다 크면 시스템은 안정된 고정점 1개와 불안정한 고정점 1개를 가진다.r이 고정점이 함께 이동하므로 r = 0에서 반안정성 고정점과 잠시 충돌한 후 r < 0이 되면 존재하지 않게 된다.
이 경우 제어 매개변수 r이 0일 때 시스템의 동작이 유의하게 변화하기 때문에 0은 분기점이 된다.r이 변화함에 따라 그림 2의 고정점 위치를 추적함으로써, 그림 3에 나타낸 분기도를 생성할 수 있다.null
다른 유형의 분기들도 역동적인 시스템에서는 중요하지만 안장 노드의 분기가 생물학에서는 가장 중요한 경향이 있다.실제 생물학적 시스템은 동적 방정식에 오차항을 도입하는 작은 확률적 변형을 따르며, 이는 대개 별도의 안장 노드와 고정 지점으로 단순화하는 복잡한 분기를 초래한다.생물학에서 나타날 수 있는 그러한 "불완전한" 분기의 두 가지 예가 아래에 설명되어 있다.오류가 있는 안장 노드 자체는 질적 동작의 변화가 없는 x-r 평면에서 간단히 해석된다는 점에 유의하십시오. 이는 아래에 제시된 것과 동일한 분석을 사용하여 증명할 수 있다.
불완전한 초임계 분리
일반적인 간단한 분기점은 다음과 같은 전임계 분기점이다.
= - dx 및 그림 4의 분기 도표(검은색 곡선)위상도는 그림 5와 같다.위상 다이어그램의 x 단위를 r 변경으로 추적하면 원점에서 교차하는 두 개의 고정점 궤적이 있다; 이것이 분기점이다(직관적으로, 위상 초상화의 x 단절 수가 변경되는 경우).왼쪽 고정점은 항상 불안정하고, 오른쪽 고정점은 안정적이다.null
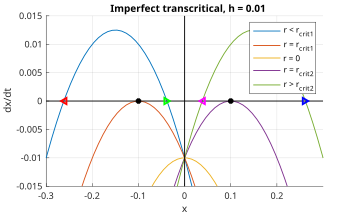
이제 오류 용어 h를 추가하는 것을 고려한다. 여기서 0 < h < 1.그것은
에러 용어는 모든 위상 초상화를 수직으로, h가 양이면 아래쪽으로 번역한다.그림 6의 왼쪽 절반(x < 0)에서 흑색, 적색, 녹색 고정점은 각각 반음계, 불안정, 안정성이 있다.이것은 오른쪽 반쪽(x > 0)에 있는 자홍색, 검정색, 파랑색 점들에 의해 미러링된다.따라서 이들 절반의 각 부분은 안장-노드 분리처럼 작용한다. 다시 말하면, 불완전한 초임계 분리는 그림 4의 빨간색 곡선에서 볼 수 있듯이 임계점에 가까울 때 두 개의 안장-노드 분기에 의해 대략적으로 추정될 수 있다.null
선형안정해석
위상 다이어그램의 흐름을 관찰하는 것 외에도 선형 안정성 분석을 사용하여 다양한 고정점의 안정성을 증명하는 것도 가능하다.먼저 위상 초상화에서 분기 방정식을 0으로 설정하여 고정점을 찾는다.
2차 공식을 사용하여 고정점 x* 찾기:
마지막 단계에서 근사치 4h << r이 사용되었으며, 이는 그림 6의 밝은 파란색과 녹색 곡선과 같은 분기점을 훨씬 지나서 고정된 점을 연구하기에 합리적이다.더 단순화하면
다음으로 위상 초상곡선이 고정점에서 증가하는지 감소하는지 여부를 결정하는데, 이는 분기 방정식의 첫 번째 파생상품에 x*를 꽂아 평가할 수 있다.null
결과는 r이 긍정적일 수 있고 부정적일 수 있다는 사실 때문에 복잡하다. 그럼에도 불구하고 각 고정점의 안정성에 관한 결론은 이전과 같다.첫 번째 파생상품은 위상 다이어그램 흐름 분석과 동일한 정보를 포함하고 있으므로 이는 놀랄 일이 아니다.위 용액의 색상은 그림 6의 화살표에 해당한다.
불완전한 피치포크 분리
앞의 버클링 빔 예는 피치 포크 분기의 예다. (아마도 더 적절하게 "트리프화"라고 불릴 것이다.)그림 7의 왼쪽에 "이상적인" 피치포크가 표시되어 있다.
그리고 r = 0은 분기가 발생하는 지점이며, 그림 8의 원점에 있는 검은색 점으로 표시된다.r이 0을 지나 증가함에 따라 검은 점은 오른쪽으로 움직이는 파란색 안정점, 왼쪽으로 움직이는 빨간색 안정점, 원점에 머무르는 세 번째 불안정한 점 등 세 개의 궤도로 갈라진다.파란색과 빨간색은 그림 7(왼쪽)의 실선이고, 검은색 불안정한 궤적은 양의 x축을 따라 점선 부분이다.null
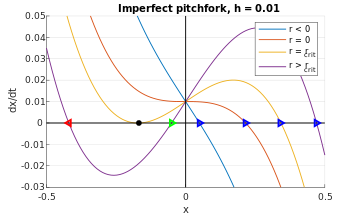
이전과 같이 오류 용어 h를 고려한다. 여기서 0 < h < 1>, 즉.
다시 한번 위상 초상화는 그림 9와 같이 극소량 위로 번역된다.위상 다이어그램의 x 절편을 r 변경으로 추적하면 고정점이 산출되며, 이는 그림 7(오른쪽)의 정성적 결과를 요약한다.좀 더 구체적으로, 그림 9의 파란색 고정점은 그림 7(오른쪽)의 위쪽 궤적에 해당한다. 녹색 고정점은 점 궤도, 빨간색 고정점은 병점 궤도다.따라서 불완전한 경우(h ≠ 0)에서 피치 포크 분리는 안장 노드의 분리와 결합된 단일 안정 고정 지점으로 단순화된다.null
2차 방정식 대신 입방정식에 일반화된 용액을 사용하는 경우를 제외하고 선형 안정성 분석도 여기에서 수행할 수 있다.The process is the same: 1) set the differential equation to zero and find the analytical form of the fixed points x*, 2) plug each x* into the first derivative , then 3) evaluate stability based on whether 이(가) 양수 또는 음수임.null
다중성
시스템에서 결합된 안장-노드 분기는 다중성을 생성할 수 있다.Bistability(다중화성의 특별한 경우)는 많은 생물학적 시스템에서 중요한 속성이며, 종종 긍정적인 피드백 상호작용과 초민감 요소의 혼합을 포함하는 네트워크 아키텍처의 결과물이다.바이스트 가능 시스템은 이력(hysteretic) 즉, 시스템 상태는 입력의 이력에 따라 달라지는데, 이는 셀룰러 프로세스의 스위치 같은 제어에 결정적일 수 있다.[2]예를 들어, 이는 셀이 특정 경로에 커밋할지 여부를 결정하는 맥락에서 중요하다. 비 이력적 응답은 활성화 임계값에 가까운 임의의 열 변동에 노출될 때 시스템을 빠르게 켜고 끌 수 있으며, 이는 자원 효율성이 떨어질 수 있다.null
생물학의 구체적인 예
역학관계에 분리가 있는 네트워크는 셀 주기의 많은 중요한 전환을 제어한다.G1/S, G2/M, 은유세-아나파아제 전환은 세포주기에서 모든 것이 생화학적 전환의 역할을 한다.예를 들어, Xenopus laevis의 달걀 추출물은 사이클린 의존성 키나제인 Cdc2의 인산화에서 긍정적인 피드백에 의해 되돌릴 수 없이 유사분열로 안팎으로 구동된다.[3]null
인구 생태학에서, 식품 웹 상호작용 네트워크의 역학관계는 Hopf 분기를 나타낼 수 있다.예를 들어, 1차 생산자, 광물 자원, 초식 동물로 구성된 수생 시스템에서, 연구원들은 인구의 평형, 순환, 멸종의 패턴이 Hopf Bifuration을 가진 단순한 비선형 모델로 정성적으로 설명될 수 있다는 것을 발견했다.[4]null
새싹 효모(S. serebisiae)에서의 갈락토오스 이용은 갈락토오스 농도의 변화 함수로 GAL 프로모터가 유도한 GFP 표현을 통해 측정할 수 있다.이 시스템은 유도 상태와 비유도 상태 사이의 균일성 전환을 나타낸다.[5]null
마찬가지로, GFP-expressing lac 프로모터가 측정한 tio-methylgalactoside(유당 아날로그) 농도의 함수로써 대장균에서의 락토오스 이용은 비스트성과 이력성을 나타낸다(그림 10, 왼쪽 및 오른쪽).[6]null
참고 항목
참조
- ^ 스트로가츠 S.H. (1994), 비선형 역학과 혼돈, 페르세우스 서적 출판
- ^ 데이비드 안젤리, 제임스 E.페렐 주니어, 에두아르도 D.손태그. 대규모 생물학적 양성 피드백 시스템에서 다중성, 분기성 및 이력 검출.PNAS 2004년 2월 17일 제101권 제7호 1822-1827호
- ^ Sha, Wei; Moore, Jonathan; Chen, Katherine; Lassaletta, Antonio D.; Yi, Chung-Seon; Tyson, John J.; Sible, Jill C. (2003-02-04). "Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts". Proceedings of the National Academy of Sciences of the United States of America. 100 (3): 975–980. doi:10.1073/pnas.0235349100. ISSN 0027-8424. PMC 298711. PMID 12509509.
- ^ 그레고르 F.루즈만, 스티븐 P. 엘너, 카일 W.셔처, 그리고 넬슨 G. 헤어스턴 주니어.살아있는 프레데터-프리 시스템에서 호프 분기점 건너기.과학. 2000년 11월 17일: 290 (5495), 1358–1360. 도이:10.1126/과학.290.5495.1358
- ^ Song C, Penix H, Abedi V, Scott M, Ingalls BP, et al. 2010 셀룰러 네트워크의 확률적 분기 구조 추정.PLoS Compute Biol 6(3): e1000699.doi:10.1371/1998.pcbi.1000699
- ^ 에르투그룰 M. 오즈부닥, 무쿤드 Thtai, Han N. Lim, 보리스 I.슈레이만과 알렉산더 판 우데나르덴.대장균의 유당 이용망 내 다중성자연.2004년 2월 19일 ;427 (6976):737–40






















 (가) 양수 또는 음수임.null
(가) 양수 또는 음수임.null