네트워크 모티브

Network motif
시리즈의 일부
네트워크 과학
Internet_map_1024.jpg
네트워크 타입
그래프
특징들
종류들
모델
토폴로지
다이내믹스
  • 리스트
  • 분류

네트워크 모티브는 반복적이고 통계적으로 유의한 하위 그래프 또는 더 큰 그래프의 패턴입니다.생물학적 네트워크, 소셜 네트워크, 기술 네트워크(예: 컴퓨터 네트워크 및 전기 회로) 등을 포함한 모든 네트워크는 다양한 하위 그래프를 포함하는 그래프로 나타낼 수 있다.

네트워크 모티브는 특정 네트워크 또는 다양한 네트워크 간에 반복되는 서브그래프입니다.정점 사이의 상호작용의 특정 패턴에 의해 정의된 이러한 하위 그래프 각각은 특정 기능이 효율적으로 달성되는 프레임워크를 반영할 수 있다.실제로 모티브는 기능적 특성을 반영할 수 있기 때문에 매우 중요하다.그것들은 최근 [1]복잡한 네트워크의 구조 설계 원리를 밝혀내는 데 유용한 개념으로 많은 주목을 받고 있다.네트워크 모티브는 네트워크의 기능적 능력에 대한 깊은 통찰력을 제공할 수 있지만, 이러한 모티브의 검출은 계산적으로 어렵다.

정의.

G = (V, E) 및 Gδ = (Vδ, Eδ)를 두 개의 그래프로 한다.그래프 G'는 V ⊆ V 、 E v E ( ( V × × V v )의 그래프 G(G g G로 표기)의 서브그래프이다.G' 'G' 및 G'가 u, v' 'E'의 모든 엣지 'u, v' 'V'를 포함하는 경우 G'는 G의 유도 서브그래프이다.우리는 바이젝션(일대일 대응)이 존재하는 경우 Gθ와 G를 동형(Gθ ↔ G로 쓴다)이라고 부른다.V' → V with u, v' eE' ⇔ f(u), f(v) ∈E 、 all u, v ∈ V 。매핑 f는 G와 [2]GΩ 사이의 동형사상이라고 불린다.

서브그래프 G'와 그래프 G' 사이에 동형성이 존재하는 경우, 이 매핑은 G에서 G'의 외관을 나타낸다.G에서 그래프 G g의 출현 횟수는 G에서 G g의 빈도G F라고 불립니다.그래프 F(G))가G 미리 정의된 임계값 또는 컷오프 값을 초과할 경우 그래프는 G에서 반복(또는 빈도)이라고 불립니다.이 리뷰에서는 용어 패턴과 빈번한 하위 그래프를 번갈아 사용합니다.G와 관련된 늘 모델에 대응하는 랜덤 그래프의 앙상블 δ(G)가 있다.δ(G)에서 N개의 랜덤 그래프를 균일하게 선택하고 G의 특정 빈도의 서브그래프 G'의 주파수를 계산해야 한다.G의 G'의 빈도가 N개의 랜덤 그래프i R의 산술 평균 주파수보다 높은 경우, 이 반복 패턴을 유의하다고 하며, 따라서 G'를 G의 모티브로 취급한다.작은 그래프 Gδ, 네트워크 G 및 일련의 랜덤화 네트워크 R(G) δδ(R)의 경우, 여기서 R(G) = N인 경우, Gδ 주파수의 Z 점수는 다음과 같이 주어진다.

여기서R μ(G))와 μR(G))는 각각 [3][4][5][6][7][8]세트 R(G)에서 주파수의 평균 및 표준 편차를 나타냅니다.Z(G),)가 클수록 모티브로서 서브그래프 G as가 더 중요하다.또는 모티브 검출에서 고려할 수 있는 또 다른 측정치는 F(G in)[6] ) F(G))의G 확률로 주어진 p-값이다R. 여기서 F(G))는R 무작위 네트워크에서 G'의 빈도를 나타낸다.p-값이 임계값(일반적으로 0.01 또는 0.05)보다 작은 하위 그래프는 유의한 패턴으로 처리됩니다.G' 주파수의 p-값은 다음과 같이 정의됩니다.

그래프에서 서브그래프가 다른 경우(M1~M4)는 그래프(a)에서 서브그래프(b)가 다른 경우이다.주파수 개념1 F의 경우 집합 M1, M2, M3, M4가 모든 일치 항목을 나타내므로1 F = 4입니다.F의 경우2 두 세트 M1, M4 또는 M2, M3 중 하나가 일치할 수 있습니다. F2 = 23. 마지막으로 주파수 개념 F의 경우 일치 중 하나(M1 ~ M4)만 허용되므로3 F = 1입니다.이들 3가지 주파수 개념의 빈도는 네트워크 요소의 사용이 제한될수록 감소합니다.

여기서 N은 랜덤화된 네트워크의 수를 나타냅니다.i는 랜덤화된 네트워크의 앙상블에 걸쳐 정의됩니다.또한 조건 c(i)가 유지되는 경우 크로네커 델타 함수 θ(c(i)는 1입니다.네트워크 G에서 특정 n 사이즈의 서브그래프 G'의 농도는[9][10] n 사이즈의 비동형 서브그래프 주파수에 대한 네트워크 내의 서브그래프 외관의 비율을 나타냅니다.이 값은 다음과 같습니다.

여기서 인덱스 i는 모든 비동형 n-사이즈 그래프 세트에 걸쳐 정의된다.네트워크 모티브를 평가하기 위해 다른 통계적 측정이 정의되지만 알려진 알고리즘에서는 거의 사용되지 않습니다.이 측정은 Picard 등에 의해 2008년에 도입되었으며 위에서 [11]암묵적으로 사용되고 있는 가우스 정규 분포가 아닌 포아송 분포를 사용했다.

또한 서브그래프 주파수의 세 가지 특정 개념이 [12]제안되었다.그림에서 보듯이 제1의 주파수1 개념 F는 원래의 네트워크에서의 그래프의 모든 일치를 고려한다.이 정의는 위에서 설명한 것과 유사합니다.두 번째 개념2 F는 원래 네트워크에서 주어진 그래프의 에지 분리 인스턴스의 최대 수로 정의됩니다.마지막으로 주파수 개념3 F는 분리된 에지 및 노드와의 매칭을 수반한다.따라서 2개의 개념3 F와2 F는 그래프 요소의 사용을 제한하고, 추론할 수 있듯이 네트워크 요소의 사용에 제한을 가함으로써 서브 그래프의 빈도는 감소합니다.그 결과 주파수 개념2 F와3 F를 고집하면 네트워크 모티브 검출 알고리즘이 더 많은 후보 서브그래프를 넘길 수 있습니다.

역사

네트워크 모티브 연구는 네트워크의 삼합회 센서스 개념을 도입한 네덜란드와 라인하르트에[13][14][15][16] 의해 개척되었다.이들은 다양한 유형의 서브그래프 구성을 열거하고 서브그래프 수가 랜덤네트워크에서 예상되는 것과 통계적으로 다른지 여부를 테스트하는 방법을 도입했다.

이 아이디어는 2002년 Uri Alon과 그의 그룹에 의해 더욱 일반화되었는데, 그 때 네트워크 모티브가 박테리아 대장균의 유전자 조절(전사) 네트워크와 그 후 대규모 자연 네트워크에서 발견되었다.그 이후로, 그 주제에 대한 상당한 수의 연구가 수행되었다.이러한 연구의 일부는 생물학적 응용에 초점을 맞추고 다른 일부는 네트워크 모티브의 계산 이론에 초점을 맞춘다.

생물학적 연구는 생물학적 네트워크에서 검출된 모티브를 해석하기 위해 노력한다.예를 들어,[17] 후속 작업에서는 대장균에서 발견된 네트워크 모티브가 효모 [21][22][23]및 상위 유기체뿐만 아니라 다른[18][19][20] 세균의 전사 네트워크에서 발견되었다.네트워크 모티브의 뚜렷한 [5][24][25]세트는 신경 네트워크와 단백질 상호작용 네트워크와 같은 다른 유형의 생물학적 네트워크에서 식별되었다.

계산 연구는 생물학적 조사를 지원하고 더 큰 네트워크를 분석할 수 있도록 기존의 모티프 감지 도구를 개선하는 데 초점을 맞추고 있다.지금까지 몇 가지 다른 알고리즘이 제공되었으며, 이 알고리즘은 다음 절에서 시간 순서대로 자세히 설명합니다.

가장 최근에 네트워크 모티브를 검출하기 위한 acc-MOTIF [26]툴이 출시되었습니다.

모티브 검출 알고리즘

네트워크 모티브(NM) 검출이라는 어려운 문제에 대해 다양한 솔루션이 제안되고 있습니다.이러한 알고리즘은 정확한 계수 방법, 샘플링 방법, 패턴 성장 방법 등 다양한 패러다임으로 분류할 수 있습니다.그러나 모티브 발견 문제는 두 가지 주요 단계로 구성된다. 첫째, 하위 그래프의 발생 횟수를 계산한 다음 하위 그래프의 유의성을 평가한다.예상한 것보다 훨씬 많이 검출된 경우 재발이 심각합니다.대략적으로 말하면 서브그래프의 예상 출현 수는 원래 네트워크와 같은 속성을 가진 랜덤네트워크의 앙상블에 의해 정의되는 늘모델에 의해 결정됩니다.

2004년까지 NM 검출의 정확한 계산 방법은 Milo [3]등이 제안한 브루트포스 방법뿐이었다.이 알고리즘은 작은 모티브를 발견하는 데는 성공했지만, 크기가 5 또는 6인 모티브를 찾기 위해 이 방법을 사용하는 것은 계산적으로 가능하지 않았다.따라서, 이 문제에 대한 새로운 접근이 필요했다.

여기서는 주요 알고리즘의 계산적 측면에 대한 검토가 제공되며 알고리즘 관점에서 관련 장점과 단점이 논의된다.

파인더

Kashtan 등은 [9]2004년에 최초의 모티브 채굴 도구인 mfinder를 출판했다.완전한 열거와 첫 번째 샘플링 방법이라는 두 가지 종류의 모티브 검색 알고리즘을 구현합니다.

샘플링 디스커버리 알고리즘은 네트워크 전체의 엣지 샘플링을 기반으로 했습니다.이 알고리즘은 유도 서브그래프의 농도를 추정하여 직접 네트워크 또는 무방향 네트워크에서 모티브 검출에 사용할 수 있습니다.알고리즘의 샘플링 절차는 사이즈가 2인 서브그래프로 이어지는 네트워크의 임의의 엣지에서 시작하여 현재 서브그래프에 부수되는 랜덤에지를 선택하여 서브그래프를 확장합니다.그 후 크기 n의 서브그래프를 얻을 때까지 랜덤 인접 에지를 계속 선택한다.마지막으로 샘플링된 서브그래프는 이들 n개 노드 사이의 네트워크에 존재하는 모든 에지를 포함하도록 확장됩니다.알고리즘이 샘플링 방식을 사용하는 경우 편향되지 않은 샘플을 채취하는 것이 알고리즘이 해결할 수 있는 가장 중요한 문제입니다.그러나 표본 추출 절차는 표본을 균일하게 추출하지 않기 때문에 카슈탄 등은 네트워크 내의 [9]다른 하위 그래프에 서로 다른 가중치를 할당하는 가중치 체계를 제안했다.체중 할당의 기본 원칙은 각 하위 그래프에 대한 샘플링 확률의 정보를 이용하는 것이다. 즉, 가능한 하위 그래프는 있을 것 같지 않은 하위 그래프에 비해 상대적으로 더 적은 가중치를 얻는다. 따라서 알고리즘은 샘플링된 각 하위 그래프의 샘플링 확률을 계산해야 한다.이 가중치 기술은 mfinder가 서브그래프의 농도를 공평하게 결정하는 데 도움이 됩니다.

완전한 검색과 뚜렷한 대조를 포함하도록 확장되었을 때 알고리즘의 연산 시간은 놀랍게도 네트워크 크기와 점근적으로 독립적이다.알고리즘의 연산시간 분석은 네트워크로부터의 크기 n의 서브그래프의 각 샘플에 대해 O(nn)가 필요하다는 것을 보여준다.한편, 각 서브그래프 샘플에 대한 그래프 동형성 문제를 해결해야 하는 샘플링된 서브그래프의 분류 시간에 대한 분석은 없다.또한 서브그래프 가중치 계산에 의해 알고리즘에 추가적인 계산 노력이 부과된다.그러나 알고리즘이 동일한 서브그래프를 여러 번 샘플링할 수 있으며,[10] 정보를 수집하지 않고 시간을 보내는 것은 피할 수 없습니다.결론적으로, 샘플링의 장점을 활용함으로써 알고리즘은 완전 검색 알고리즘보다 더 효율적으로 수행되지만, 대략적인 부분 그래프 농도를 결정할 뿐이다.이 알고리즘은 주요 구현으로 인해 6 사이즈까지 모티브를 찾을 수 있으며, 그 결과 다른 모든 모티브가 아닌 가장 중요한 모티브를 제공합니다.또한 이 도구에는 시각적 표시 옵션이 없습니다.샘플링 알고리즘은 다음과 같이 간략하게 표시됩니다.

파인더
정의:꺾인 모서리 세트를 아이즈로 합니다s.V는s E의 모서리에 접촉하는 모든 노드의 집합입니다.
V와s E를 빈 집합으로 초기화합니다s.

1. 임의 에지1 e = (vi, vj)를 선택합니다.업데이트s E = {e1}, Vs = {vi, vj}

2. E의 모든s 인접 엣지 리스트 L을 작성합니다.L에서 V의 구성원s 사이의 모든 모서리를 생략합니다.

3. L에서 임의 에지 e = {vk,vl}를 선택합니다.업데이트s E = Es ⋃ {e}, Vs = Vs ⋃ {vk, vl}.

4. n-노드 하위 그래프가 완료될 때까지 2-3단계를 반복합니다(Vs = n까지).

5. 선택한 n노드 서브그래프를 샘플링할 확률을 계산합니다.

FPF(마비스토)

Schreiber와 Schwöbbermeyer는 입력 네트워크의 빈번한 서브그래프를 추출하기 위한 FPF(Flexible Pattern Finder)라는 알고리즘을 제안하여 Mavisto라는 [27]시스템에 구현했습니다.이러한 알고리즘은 주파수 개념2 F 및3 F에 적용되는 하향 폐쇄 특성을 이용합니다.하향 폐쇄 속성은 하위 그래프의 빈도가 하위 그래프의 크기를 늘림으로써 단조롭게 감소한다고 단언합니다. 단, 이 속성은1 주파수 개념 F에 반드시 유지되는 것은 아닙니다.FPF는 다른 그래프(또는 패턴)를 나타내는 노드로 이루어진 패턴 트리(그림 참조)에 근거하고 있습니다.여기서 각 노드의 상위는 하위 노드의 하위 그래프입니다.즉, 상위 노드의 그래프에 새로운 에지를 추가함으로써 각 패턴 트리 노드의 대응하는 그래프가 확장됩니다.

FPF [12]알고리즘의 패턴트리 그림

우선 FPF 알고리즘은 패턴 트리의 루트에 위치한 서브그래프의 모든 일치 정보를 열거하여 유지한다.그런 다음 대상 그래프에서 일치하는 에지에 의해 지원되는 하나의 에지를 추가하여 패턴 트리 내의 이전 노드의 하위 노드를 하나씩 구축하고 일치에 대한 모든 이전 정보를 새로운 하위 그래프(자 노드)로 확장하려고 합니다.다음 단계에서는 현재 패턴의 주파수가 미리 정의된 임계값보다 낮은지 여부를 판단한다.FPF가 더 낮고 하향 폐쇄가 유지되면 FPF는 해당 경로를 포기하고 트리의 이 부분을 더 이상 통과하지 않을 수 있으므로 불필요한 계산이 회피됩니다.그 결과 불필요한 계산이 회피됩니다.이 절차는 트래버스할 경로가 남아 있지 않을 때까지 계속됩니다.

알고리즘의 장점은 빈도가 낮은 서브그래프를 고려하지 않고 가능한 한 빨리 열거 프로세스를 완료하려고 한다는 것입니다.따라서 패턴 트리의 유망한 노드에 대해서만 시간을 할애하고 다른 모든 노드를 폐기합니다.부가적인 보너스로서 패턴 트리 개념은 패턴 트리의 각 경로를 독립적으로 통과할 수 있기 때문에 FPF를 병렬로 구현 및 실행할 수 있도록 한다.단, FPF는 주파수 개념2 F와3 F에 가장 유용합니다.하향 폐쇄는 F에 적용되지1 않기 때문입니다.그럼에도 불구하고 알고리즘이 병렬로 실행되는 경우 패턴 트리는 여전히 F에 대해1 실용적입니다.이 알고리즘의 또 다른 장점은 이 알고리즘의 구현에 모티브 크기에 제한이 없기 때문에 보다 쉽게 개선할 수 있다는 것입니다.FPF(Mavisto)의 의사 코드를 다음에 나타냅니다.

마비스토
데이터: 그래프 G, 대상 패턴 크기 t, 주파수 개념 F

결과: 최대 주파수로 t사이즈 패턴의 R을 설정합니다.

Rmax ← ,, f ← 0

P ← 사이즈 1의 시작 패턴 p1

Mp1 ← G에서 p의 모든1 일치

하는 동안에 P ≠ φ 하다

Pmax ← 최대 크기를 가진 모든 패턴을 P에서 선택합니다.

P ← P에서 최대max 주파수의 패턴을 선택합니다.

δ = ExtensionLoop (G, pp, M)

Foreach 패턴 p eE

한다면 F = F1 그리고나서 f ← 크기(Mp)

또 다른 f ← 최대 독립 세트(F, Mp)

끝.

한다면 size(p) = t 그리고나서

f = f이면max R ← R { {p}

그렇지 않으면 f > f이면max R ← {p}, fmax ← f

끝.

또 다른

F = F1 또는 f ≥ f이면max P ← P { {p}

끝.

끝.

끝.

끝.

ESU(FANMOD)

카슈탄 등의 표본 편향은 NM 발견 문제에 대한 더 나은 알고리즘을 설계하는 데 큰 자극을 주었다.카슈탄 등은 가중치 체계를 통해 이 단점을 해결하려고 했지만, 이 방법은 실행 시간에 바람직하지 않은 오버헤드를 가할 뿐만 아니라 더 복잡한 구현도 가했다.이 도구는 시각 옵션을 지원하며 시간에 대한 효율적인 알고리즘이기 때문에 가장 유용한 도구 중 하나입니다.다만, 툴의 실장 방식상 9 사이즈 이상의 모티브를 검색할 수 없기 때문에 모티브 사이즈에 제한이 있습니다.

Wernicke는 mfinder에 [9]비해 대폭 개선된 RAND-ESU라는 알고리즘을 도입했다.이 알고리즘은 정확한 열거 알고리즘 ESU를 기반으로 FANMOD라고 [10]불리는 어플리케이션으로 구현되어 있습니다.LAND-ESU는 다이렉트네트워크와 비다이렉트네트워크 양쪽에 적용할 수 있는 NM 디스커버리 알고리즘으로 네트워크 전체에서 편향되지 않은 노드샘플링을 효과적으로 이용하여 서브그래프를 여러 번 오버카운트 하는 것을 방지합니다.더욱이, RAND-ESU는 임의 네트워크의 앙상블을 Null 모델로 사용하는 대신 하위 그래프의 중요도를 결정하기 위해 DIRECT라고 불리는 새로운 분석 접근법을 사용합니다.DIRECT 방식에서는 랜덤네트워크를 [10]명시적으로 생성하지 않고 서브그래프의 집중도를 추정합니다.경험적으로, DIRECT 방법은 농도가 매우 낮은 하위 그래프의 경우 랜덤 네트워크 앙상블에 비해 더 효율적이지만, 고전적인 Null-모델은 고농축 하위 [3][10]그래프에 대한 DIRECT 방법보다 빠르다.다음에서는 ESU 알고리즘을 자세히 설명한 후 이 정확한 알고리즘을 서브그래프의 농도를 추정하는 LAND-ESU로 효율적으로 수정하는 방법을 보여 줍니다.

알고리즘 ESU와 RAND-ESU는 매우 단순하기 때문에 구현이 용이합니다.ESU는 먼저 크기 k의 모든 유도 서브그래프 세트를 찾습니다.S를 이 세트로 하겠습니다k.ESU는 재귀 함수로 구현할 수 있습니다.이 함수의 실행은 ESU-Tree라고 불리는 깊이k의 트리 같은 구조로 표시할 수 있습니다(그림 참조).각 ESU-Tree 노드는 연속된2 세트의 SUB와 EXT를 수반하는 재귀 함수의 상태를 나타냅니다.SUB는 인접한 대상 네트워크에서 SUB k k 크기의 부분 서브그래프를 확립하는 노드를 말한다. SUB = k이면 유도 완전 서브그래프를 찾은 것이므로 Sk = SUB sk S. 단, SUB < k이면 알고리즘은 SUB를 확장하여 카디널리티 k를 달성해야 한다.이는 다음 두 가지 조건을 충족하는 모든 노드를 포함하는 EXT 세트에 의해 수행됩니다.첫째, EXT의 각 노드는 SUB의 적어도1개의 노드에 인접해 있어야 합니다.둘째, 수치라벨은 SUB의 첫 번째 요소의 라벨보다 커야 합니다.첫 번째 조건에서는 SUB 노드의 확장에 의해 접속 그래프가 생성되고 두 번째 조건에서는 ESU-Tree Leave(그림 참조)가 구별되므로 오버카운트를 방지할 수 있습니다.EXT 세트는 스태틱세트가 아니기 때문에 각 단계에서 두 가지 조건을 위반하지 않는 새로운 노드만큼 확장될 수 있습니다.ESU의 다음 단계는 ESU-트리 잎에 배치된 하위 그래프를 비동형 크기 k 그래프 클래스로 분류하는 것이다. 따라서 ESU는 하위 그래프 빈도와 농도를 결정한다.이 단계는 그래프 동형 테스트를 수행하여 각 [28][29]하위 그래프를 분류하는 McKay의 노티 알고리즘을 사용하여 간단히 구현되었습니다.따라서 ESU는 재귀 알고리즘에 의해 목표 그래프에서 유도된 모든 k-사이즈 서브그래프의 집합을 찾은 다음 효율적인 도구를 사용하여 빈도를 결정한다.

LAND-ESU의 실장 순서는 매우 간단하며 FANMOD의 주요 장점 중 하나입니다.ESU 알고리즘은 ESU 트리의 각 레벨에 대해 확률값 0 pd p 11을 적용하여 ESU 트리의 일부만을 탐색하도록 변경할 수 있으며 ESU는 d-1 레벨의 노드의 각 자녀 노드를 확률d p로 통과하도록 할 수 있습니다.이 새로운 알고리즘은 RAND-ESU라고 불립니다.분명히 모든 레벨에서 p=1일d 때 RAND-ESU는 ESU와 같이 동작합니다.p=0일 경우d 알고리즘은 아무것도 찾지 못합니다.이 절차에서는 ESU-Tree의 각 리프를 방문할 확률이 같게 되어 네트워크를 통한 서브그래프의 바이어스 없는 샘플링이 이루어지는 것에 주의해 주십시오.각 리프를 방문할 확률은 δp이며dd, 이는 모든 ESU 트리 리프에서 동일합니다.따라서 이 방법을 사용하면 네트워크로부터의 서브그래프의 공평한 샘플링이 보증됩니다.그럼에도 불구하고, 1 µ d µ k에 대한d p 값의 결정은 하위 그래프 [8]농도의 정확한 결과를 얻기 위해 전문가가 수동으로 결정해야 하는 또 다른 문제이다.이 문제에 대한 명확한 규범은 없지만, 베르니케는 p_d 값을 결정하는 데 도움이 될 수 있는 몇 가지 일반적인 관찰을 제공합니다.요약하면 RAND-ESU는 편향되지 않은 샘플링 방법을 지원하는 유도 서브그래프의 경우 NM 검출을 위한 매우 빠른 알고리즘입니다.메인 ESU 알고리즘 등 FANMOD 툴은 유도 서브그래프를 검출하는 것으로 알려져 있지만 ESU에 대한 사소한 수정이 있어 비유도 서브그래프를 검출할 수도 있습니다.ESU(FANMOD)의 의사 코드를 다음에 나타냅니다.

ESU 열거(FANMOD)
Enumerate Subgraphs(G,k)

입력: 그래프 G = (V, E) 및 정수 1 µ k µ V.

출력: G의 모든 size-k 서브그래프.

각 꼭지점 v v V do에 대해

VExtension ← {u † N({v}) u > v}

불러 Extend Subgraph({v}, VExtension, v)

끝장

Extend Subgraph(VSUBgraph, VExtension, v)

VSubgraph = k이면 G[VSubgraph]를 출력하고 반환한다.

하는 동안에 VExtension » 하다

VExtension에서 임의로 선택한 정점 w를 제거합니다.

VExtension ve ← VExtension { {u nexcl N （ w 、 VSubgraph ）u > v }

불러 Extend Subgraph(VSUBgraph { {w}, VExtension ,, v)

돌아가다

니모파인더

Chen 등은 새로운 NM 발견 알고리즘인 NeMoFinder를 도입했다.NeMoFinder는 SPIN의 아이디어를 채택하여 빈번한 나무를 추출한 후 비동형 [8]그래프로 확장한다.NeMoFinder는 입력 네트워크를 크기 n의 그래프 모음으로 분할하기 위해 빈번한 크기 n의 서브그래프를 완전한 크기 n의 그래프n K가 될 때까지 에지별로 확장하여 빈번한 크기 n의 서브그래프를 찾습니다.이 알고리즘은 비다이렉트네트워크에서 NM을 검출하여 유도 서브그래프만 추출하는 것에 한정되지 않습니다.또한 NeMoFinder는 정확한 열거 알고리즘이며 샘플링 방법에 기초하지 않습니다.Chen 등의 주장처럼, NemoFinder는 저자의 [32]주장대로 S. cerevisiae (yeast) PPI 네트워크 전체에서 최대 12사이즈의 NM을 검출하는 비교적 큰 NM을 검출하는 데 적용할 수 있다.

NeMoFinder는 세 가지 주요 단계로 구성됩니다.먼저, 빈번한 크기 n 트리를 찾아낸 후 반복적인 크기 n 트리를 이용하여 전체 네트워크를 크기 n 그래프 집합으로 나눈 다음, 마지막으로, 빈번한 크기 n 서브 그래프를 [30]찾기 위한 서브 그래프 결합 연산을 수행합니다.첫 번째 단계에서 알고리즘은 모든 비동형 크기 n 트리 및 트리에서 네트워크로의 매핑을 검출한다.두 번째 단계에서는 이러한 매핑 범위를 사용하여 네트워크를 size-n 그래프로 분할합니다.이 단계까지는 NeMoFinder와 정확한 열거 방법을 구분하지 않습니다.그러나 비동형 크기 n 그래프의 상당 부분은 여전히 남아 있다.NeMoFinder는 경험적 접근 방식을 이용하여 이전 단계에서 얻은 정보를 기준으로 트리 이외의 size-n 그래프를 열거합니다.알고리즘의 주요 장점은 이전에 열거된 하위 그래프에서 후보 하위 그래프를 생성하는 세 번째 단계입니다.이러한 새로운 size-n 서브그래프는 사촌 서브그래프라고 불리는 자체에서 파생 서브그래프와 각각의 이전 서브그래프를 결합함으로써 이루어진다.이러한 새 하위 그래프에는 이전 하위 그래프와 비교하여 한 개의 추가 가장자리가 포함됩니다.단, 새로운 서브그래프 생성에는 몇 가지 문제가 있습니다.그래프에서 사촌을 도출하는 명확한 방법은 없습니다.서브그래프를 사촌과 결합하면 특정 서브그래프를 여러 번 생성할 때 용장성이 생깁니다.사촌 판정은 조인 조작으로 닫히지 않는 인접 행렬의 표준적인 표현에 의해 이루어집니다.NeMoFinder는 무방향 그래프로 나타나는 단백질-단백질 상호작용 네트워크에 대해서만 최대 12사이즈 모티브를 위한 효율적인 네트워크 모티브 검색 알고리즘입니다.또한 복잡한 생물학적 네트워크 분야에서 매우 중요한 다이렉트 네트워크에서는 사용할 수 없습니다.NeMoFinder의 유사 코드는 다음과 같습니다.

니모파인더
입력:

G - PPI 네트워크

N - 랜덤화된 네트워크의 수

K - 최대 네트워크 모티브 크기

F - 주파수 임계값;

S - 고유 임계값

출력:

U - 반복적이고 고유한 네트워크 모티브 세트

D ← ;;

3에서 K do까지의 모티브 크기 k의 경우

T ← FindRepeated(찾기 반복)나무(k);

GDk ← Graph Partition(G, T)

D ← D t T;

Dµ ← T;

i ← k;

하는 동안에 D ≠ ≠ 그리고. i † k × (k - 1) / 2 하다

Dµ ← FindRepeatedGraphs(k, i, Dµ);

D ← D ∪ D ; D ;

i ← i + 1;

도중에 끝나다

으로 끝나다.

1에서 N까지의 카운터 i의 경우

Grand ← 랜덤화 네트워크 생성();

각각에 대해서 g † D 하다

GetRandFrequency(g, Grand);

으로 끝나다.

으로 끝나다.

U ← ;;

각각에 대해서 g † D 하다

s ← GetUniqunessValue(g);

한다면 s † S 그리고나서

U ← U ∪ {g};

이면 끝이다

으로 끝나다.

U를 반환하다

그로초-켈리스

Grochow와 Kellis는 하위 그래프 모양을 열거하는 정확한 알고리즘을 제안했다.이 알고리즘은 모티브 중심 접근법에 기초하고 있습니다.즉, 쿼리 그래프라고 불리는 특정 서브그래프의 빈도는 쿼리 그래프에서 대규모 네트워크에 대한 가능한 모든 매핑을 검색함으로써 완전히 결정됩니다.네트워크 중심 방식과 비교하여 모티브 중심 방식에는 몇 가지 유익한 특징이 있다고 주장되고 있습니다.우선 서브그래프 열거의 복잡성 증가를 회피한다.또, 열거하는 대신에 매핑을 이용하는 것으로, 동형 테스트의 향상을 가능하게 한다.알고리즘의 성능을 향상시키기 위해, 저자들은 대칭 파괴 조건이라고 불리는 빠른 방법을 도입했다.간단한 서브그래프 동형성 테스트 중에 서브그래프는 쿼리 그래프의 동일한 서브그래프에 여러 번 매핑될 수 있다.Grochow-Kellis(GK) 알고리즘에서는 이러한 다중 매핑을 피하기 위해 대칭 브레이크가 사용됩니다.여기서는 GK 알고리즘과 중복된 동형성 테스트를 제거하는 대칭 파괴 조건을 소개한다.

(a) 그래프 G, (b) (a)에 나타내는 G의 모든 자기 동형의 그림.세트 AutG에서 (c)의 SymG에 의해 주어진 G의 대칭 파괴 조건 세트를 얻을 수 있다.AutG의 첫 번째 매핑만이 SynG 조건을 충족합니다.그 결과, Isomorphism Extension 모듈에 SymG를 적용함으로써 알고리즘은 네트워크 내의 일치 가능한 각 서브그래프를 G에 1회만 열거합니다.SynG는 반드시 임의의 그래프 G에 대해 하나의 집합은 아닙니다.

GK 알고리즘은 두 가지 주요 단계로 특정 쿼리 그래프의 네트워크에 대한 매핑세트 전체를 검출합니다.쿼리 그래프의 대칭 해제 조건 계산에서 시작합니다.다음으로 분기 및 경계 방법을 사용하여 알고리즘은 쿼리 그래프에서 관련된 대칭 파괴 조건을 충족하는 네트워크에 대한 가능한 모든 매핑을 찾으려고 합니다.GK 알고리즘에서의 대칭 파괴 조건의 사용 예를 그림에 나타낸다.

위에서 설명한 바와 같이 대칭을 [33][34]깨는 기술은 대칭으로 인해 하위 그래프를 찾는 데 여러 번 시간을 할애하지 않는 단순한 메커니즘입니다.대칭을 깨는 조건을 계산하려면 특정 쿼리 그래프의 모든 자기동형을 찾아야 합니다.그래프 자기동형 문제에 대한 효율적인(또는 다항식 시간) 알고리즘은 없지만, McKay의 도구를 [28][29]통해 실제로 이 문제를 효율적으로 해결할 수 있습니다.주장대로 NM 검출에 대칭 파괴 조건을 사용하면 실행 시간을 크게 절약할 수 있습니다.게다가 대칭 파괴 조건을 사용하면, 특히 무방향 네트워크에 비해 다이렉트 네트워크의 효율이 높다는 점에서, 그 결과로부터 추측할 수 있다.GK 알고리즘에서 사용되는 대칭 해제 조건은 ESU 알고리즘이 EXT 및 SUB 세트의 라벨에 적용되는 제한과 유사합니다.결론적으로 GK 알고리즘은 대규모 복잡한 네트워크에서 주어진 쿼리 그래프의 정확한 출현 수를 계산하고 대칭 파괴 조건을 이용하여 알고리즘 성능을 향상시킨다.또한 GK 알고리즘은 구현 시 모티브 크기에 제한이 없는 알려진 알고리즘 중 하나이며 잠재적으로 모든 크기의 모티브를 찾을 수 있습니다.

컬러 코딩 접근법

NM 디스커버리 분야의 대부분의 알고리즘은 네트워크의 유도 서브그래프를 찾기 위해 사용됩니다.2008년에 노가 알론 외 연구진은 비유도 하위 그래프를 찾기 위한 접근방식을 도입했다.이러한 기술은 PPI와 같은 무방향 네트워크에서 작동합니다.또한 비유발 트리 및 경계 트리 폭 하위 그래프를 카운트한다.이 방법은 크기가 최대 10개인 하위 그래프에 적용됩니다.

이 알고리즘은 n개의 정점이 있는 네트워크 G에서 k = O(logn) 정점이 있는 트리 T의 비유발 발생 횟수를 다음과 같이 카운트합니다.

  1. 컬러 코딩.입력 네트워크 G의 각 정점에 k개의 색상 중 하나로 랜덤으로 독립적으로 균일하게 색을 입힌다.
  2. 세고 있다.동적 프로그래밍 루틴을 적용하여 각 정점이 고유한 색상을 갖는 T의 비유발 발생 횟수를 계산합니다.이 순서의 상세한 것에 대하여는,[35] 을 참조해 주세요.
  3. 위의 두 단계를 O(ek)회 반복하고 T의 발생 횟수를 더하여 G에서의 발생 횟수를 추정한다.

사용 가능한 PPI 네트워크는 완전하지 않고 오류가 없기 때문에 이러한 네트워크의 NM 디스커버리에 적합합니다.Grochow-Kellis 알고리즘과 이 알고리즘은 비유도 서브그래프에 널리 사용되는 알고리즘이기 때문에 Alon 등이 도입한 알고리즘은 Grochow-Kellis [35]알고리즘보다 시간이 적게 걸린다는 점을 언급할 필요가 있다.

모다

Omidi 등은 유도 및 비유도 NM 발견에 적용할 수 있는 MODA라는 모티브 검출을 위한 새로운 알고리즘을 도입했다.Grochow-Kellis 알고리즘 섹션에서 설명한 모티브 중심 접근법에 기초하고 있습니다.MODA 및 GK 알고리즘과 같은 모티브 중심 알고리즘을 구별하는 것은 매우 중요합니다. 쿼리 검색 알고리즘으로 작동할 수 있기 때문입니다.이 기능을 사용하면 이러한 알고리즘이 단일 모티브 쿼리 또는 크기가 더 큰 소수의 모티브 쿼리(일부 가능한 특정 크기의 하위 그래프만)를 찾을 수 있습니다.가능한 비동형 서브그래프의 수가 서브그래프 크기에 따라 기하급수적으로 증가함에 따라 대형 모티브(10개보다 큰 경우)의 경우 모든 가능한 서브그래프를 찾는 네트워크 중심 알고리즘이 문제에 직면하게 됩니다.모티브 중심 알고리즘은 가능한 모든 큰 크기의 하위 그래프를 발견하는 데 문제가 있지만, 적은 수의 하위 그래프를 찾는 능력은 때때로 중요한 특성이다.

확장 트리라고 불리는 계층 구조를 사용하여 MODA 알고리즘은 약속 없는 서브 그래프가 열거되지 않도록 하는 FPF와 유사한 크기의 NM을 체계적으로 추출할 수 있습니다.MODA는 빈번한 서브 그래프가 발생할 수 있는 잠재적인 쿼리(또는 후보 서브 그래프)를 고려합니다.MODA는 트리 형태의 구조를 이용하는 것에 있어서 FPF와 유사하지만, 확장 트리는 주파수 개념1 F의 계산에만 적용할 수 있다.다음에 논의하는 바와 같이, 이 알고리즘의 장점은 비트리 쿼리 그래프에 대해 서브그래프 동형성 테스트를 수행하지 않는다는 것입니다.또, 알고리즘의 실행 시간을 고속화하기 위해서 샘플링 방법을 이용한다.

여기 주요 아이디어가 있다: 간단한 기준으로 네트워크에 대한 k-사이즈 그래프의 동일한 크기의 슈퍼그래프에 대한 매핑을 일반화할 수 있다.예를 들어 그래프 G의 f(G)와 k노드가 네트워크에 매핑되어 있으며, 같은 크기의 그래프 G'에 엣지 &langu, v'가 1개 더 있다고 가정합니다.네트워크G 내에 엣지 'fG(u, f(v)'가G 있는 경우 f는 G'를 네트워크에 매핑합니다.그 결과, 우리는 서브그래프 동형성 테스트를 수행하지 않고도 O(1) 시간 내에 동일한 순서의 슈퍼그래프의 주파수를 결정하기 위해 그래프의 매핑 세트를 이용할 수 있다.이 알고리즘은 크기가 k인 최소로 연결된 쿼리 그래프에서 독창적으로 시작하여 서브그래프 동형성을 통해 네트워크에서 매핑을 찾습니다.그 후 그래프 크기를 고려하여 이전에 고려했던 쿼리 그래프를 에지별로 확장하여 위와 같이 확장 그래프의 빈도를 계산한다.그 팽창 과정 Kk(완전히.mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output과 .sr-only{연결되어 완전한 그래프에 도달할 때까지 계속되고 있다.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}k(k-1)⁄2 가장자리 cm이다.

전술한 바와 같이 알고리즘은 네트워크 내의 서브트리 주파수를 계산하는 것으로 시작하여 서브트리를 엣지별로 확장합니다.이 아이디어를 구현하는 한 가지 방법은 각 k에 대한 확장 트리k T라고 불립니다.그림은 사이즈 4 서브그래프의 확장 트리를 나타내고 있습니다.T는k 실행 중인 프로세스를 정리하고 계층적으로 쿼리 그래프를 제공합니다.엄밀히 말하면, 확장 트리k T는 단순히 directed acyclic graph 또는 DAG이며, 루트 번호 k는 확장 트리 내에 존재하는 그래프 크기를 나타내며, 다른 노드 각각은 별개의 k-size 쿼리 그래프의 인접 행렬을 포함한다.T의k 첫 번째 레벨의 노드는 모두 별개의 k-사이즈 트리이며, T를 상세하게 통과함으로써k 쿼리 그래프는 각 레벨에서 1개의 엣지로 확장됩니다.노드의 쿼리 그래프는 노드 자식의 쿼리 그래프의 하위 그래프로, 1개의 엣지 차이가 있습니다.T에서k 가장 긴 경로는 (k-3k2+4)/2개의 에지로 구성되어 있으며 완전한 그래프를 유지하는 루트에서 리프 노드까지의 경로입니다.확장 트리의 생성은 [36]에 설명되어 있는 간단한 루틴으로 수행할 수 있습니다.

MODA는 T를 통과하여k T의 첫k 번째 레벨에서 쿼리 트리를 추출할 때 매핑세트를 계산하고 다음 단계를 위해 이들 매핑을 저장합니다.T로부터의k 비트리 쿼리의 경우 알고리즘은 T 내의k 부모 노드에 관련된 매핑을 추출하여 이들 매핑 중 현재 쿼리 그래프를 지원할 수 있는 매핑을 결정합니다.알고리즘이 완전한 쿼리 그래프를 얻을 때까지 프로세스는 계속됩니다.쿼리 트리 매핑은 Grochow-Kellis 알고리즘을 사용하여 추출됩니다.비트리 쿼리 그래프의 빈도를 계산하기 위해 알고리즘은 O(1) 단계를 수행하는 단순한 루틴을 사용합니다.또한 MODA는 네트워크 내의 각 노드의 샘플링이 노드 정도에 선형 비례하는 샘플링 방법을 이용하며, 확률 분포는 복잡한 네트워크 분야에서 [37]잘 알려진 Barabasi-Albert 우선 어태치먼트 모델과 정확히 유사하다.이 방법에서는 근사치가 생성되지만 서브 그래프가 고도로 연결된 [38]노드 주위에 집약되기 때문에 다른 실행에서 결과가 거의 안정적입니다.MODA 의 유사 코드를 다음에 나타냅니다.

4 노드 쿼리 그래프용 확장 트리 T4의 그림.제1레벨에는 비동형 k사이즈 트리가 있으며 각레벨에서는 부모그래프에 엣지를 가산하여 자녀그래프를 형성한다.두 번째 레벨에는 빨간색 파선으로 표시된 두 개의 대체 에지가 있는 그래프가 있습니다.실제로 이 노드는 [36]동형인 두 개의 확장된 그래프를 나타냅니다.
모다
입력: G:입력 그래프, k: 서브 그래프 크기, δ: 임계값

출력: 자주 사용되는 서브그래프 목록: 모든 자주 사용되는 k 크기 서브그래프 목록

주의G: F: 입력 그래프 G의 G로부터의 매핑 세트

가지고 오다 Tk.

하다

G's = Get-Next-BFS(Tk) // G's는 쿼리 그래프입니다.

E(G) = (k – 1)인 경우

불러 매핑 모듈(G', G)

또 다른

불러 열거 모듈(Gk', G, T)

이면 끝이다

절약하다 에프2

한다면 FG > δ 그리고나서

G'를 자주 사용하는 서브그래프 목록에 추가

이면 끝이다

까지 E(G') = (k – 1)/2

자주 사용되는 서브그래프 목록 반환

카보시

최근에 도입된 Kavosh라는 알고리즘은 메인 메모리 사용률 개선을 목표로 하고 있습니다.Kavosh는 다이렉트네트워크와 비다이렉트네트워크 양쪽에서 NM을 검출하는데 사용할 수 있습니다.열거의 주요 개념은 GK 및 MODA 알고리즘과 유사합니다.이 알고리즘은 먼저 특정 노드가 참여한 모든 k-size 서브그래프를 찾은 후 노드를 제거한 후 [39]나머지 노드에 대해 이 프로세스를 반복합니다.

특정 노드를 포함하는 크기 k의 서브그래프를 계산하기 위해 이 노드에 뿌리를 두고 근린관계에 기초한 최대 깊이 k의 트리가 암묵적으로 구축된다.각 노드의 자녀에는 착신 및 발신 인접 노드가 모두 포함됩니다.트리를 하강하기 위해 상위 레벨에 포함되지 않은 경우에만 특정 어린이를 포함할 수 있다는 제한이 있는 각 레벨에서 하위 항목이 선택됩니다.가능한 한 낮은 레벨로 하강한 후 트리가 다시 상승하고 하위 경로에서 방문한 노드가 현재 방문되지 않은 노드로 간주된다는 조건으로 프로세스를 반복합니다.트리 구축의 마지막 제한사항은 특정 트리 내의 모든 어린이가 트리 루트 라벨보다 큰 숫자 라벨을 가져야 한다는 것입니다.하위 레이블의 제한은 GK 및 ESU 알고리즘이 하위 그래프의 과다 카운트를 피하기 위해 사용하는 조건과 유사합니다.

하위 그래프를 추출하기 위한 프로토콜은 정수의 구성을 사용합니다.크기 k의 하위 그래프를 추출하기 위해서는 k-1 정수의 가능한 모든 구성을 고려해야 한다.k-1의 구성은 k-1을 양의 정수의 합으로 표현하는 모든 가능한 방법으로 구성된다.합계 순서가 다른 합계는 구별되는 것으로 간주됩니다.조성물은 k, k3, …, k로2m 표현될 수 있다. 여기서2 k + k3 + ... + km = k-1.해당 조성에 기초하여 서브스트림을 카운트하기 위해i 트리의 i번째 레벨에서 k개의 노드를 서브스트리의 노드(i = 2,3,...m)로 선택한다.k-1 선택 노드는 루트의 노드와 함께 네트워크 내의 서브그래프를 정의합니다.Kavosh는 대상 네트워크에서 일치하는 서브그래프를 검출한 후 대상 네트워크에 따라 각 클래스의 크기를 평가할 수 있도록 FANMOD와 같은 방법으로 nauty 알고리즘을 사용합니다.Kavosh 알고리즘의 열거 부분은 다음과 같습니다.

카보시 목록
Enumerate_Vertex(G, u, S, 나머지, i)

입력: G:입력 그래프
u: 루트 정점
S: 선택(S = { S0,S1, ...,Sk-1}는 모든i S 집합의 배열)
나머지: 선택할 나머지 정점의 수
i: 트리의 현재 깊이.
출력: 그래프 G의 모든 k-사이즈 서브그래프는 u에 뿌리를 두고 있습니다.

한다면나머지 = 0그리고나서
돌아가다
또 다른
ValList ← Validate(G, Si-1, u)
ni ← 최소(ValList, 나머지)
위해서ki = 1로.ni하다
C ← Initial_Comb(ValList, ki)
(이에 따라 첫 번째 정점 조합을 선택)
따라하다
Si ← C
Enumerate_Vertex(G, u, S, Remaining-ki, i+1)
Next_Comb(밸리스트i, k)
(이에 따라 다음 정점 조합을 선택합니다.
까지C = NIL
으로 끝나다.
각각에 대해서v » Val List(밸리스트)하다
방문[v] ← 거짓
으로 끝나다.
이면 끝이다

검증(G, 부모, u)

입력:G: 입력 그래프, 부모: 마지막 레이어의 선택된 정점, u: 루트 정점.
출력: 현재 수준의 유효한 정점입니다.

ValList ← NILL
각각에 대해서 v § 부모 하다
각각에 대해서 w neighbor 네이버[u] 하다
한다면 label[u] < 라벨[w] 하지 않다 방문[w] 그리고나서
방문[w] ← 참
ValList = ValList + w
이면 끝이다
으로 끝나다.
으로 끝나다.
돌아가다 ValList

최근에는 CytoKavosh라는 Cytoscape 플러그인이 이 소프트웨어를 위해 개발되었습니다.Cytoscape 웹 페이지 [1]를 통해 이용할 수 있습니다.

G-Tries

2010년에 페드로 리베이로와 페르난도 실바는 g-trie라고 [41]불리는 하위 그래프 모음을 저장하기 위한 새로운 데이터 구조를 제안했다.개념적으로 접두사 트리와 유사한 이 데이터 구조는 구조에 따라 하위 그래프를 저장하고 더 큰 그래프에서 각 하위 그래프의 발생을 찾습니다.이 데이터 구조의 주목할 만한 측면 중 하나는 네트워크 모티브의 검출을 위해 메인 네트워크 내의 서브 그래프가 평가되어야 한다는 것입니다.따라서 메인 네트워크에 없는 랜덤네트워크를 찾을 필요가 없습니다.이는 랜덤 네트워크 내의 모든 서브그래프가 파생되는 알고리즘에서 시간이 많이 걸리는 부분 중 하나입니다.

g-trie는 그래프 모음을 저장할 수 있는 다중 방향 트리입니다.각 트리 노드는 단일 그래프 정점과 상위 노드에 대응하는 에지에 대한 정보를 포함한다.루트에서 리프까지의 경로는 단일 그래프에 해당합니다.g-trie 노드의 하위 노드는 공통 하위 그래프를 공유합니다.g-trie의 구성은 에 잘 설명되어 있습니다.[41]g-trie 구성 후 계수부가 발생한다.계수 과정의 주요 아이디어는 가능한 모든 하위 그래프로 역추적하는 것이지만, 동시에 동형성 테스트를 수행합니다.이 역추적 기법은 기본적으로 MODA 및 GK 알고리즘과 같은 다른 모티브 중심 접근법에 사용되는 것과 동일한 기법이다.특정 시간에 여러 다른 후보 하위 그래프에 부분 동형 매치가 있다는 의미에서 공통 하위 구조를 활용합니다.

전술한 알고리즘 중 G-Tries가 가장 빠르다.그러나 메모리를 과도하게 사용하는 것이 이 알고리즘의 단점이며, 평균 메모리를 가진 개인용 컴퓨터가 검출 가능한 모티브의 크기를 제한할 수 있습니다.

ParaMODA 및 NemoMap

ParaMODA와[42] NemoMap은[43] 각각 2017년과 2018년에 발표된 고속 알고리즘입니다.다른 [44]많은 제품보다 확장성이 떨어집니다.

비교

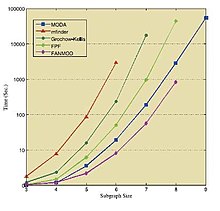
다음 표와 그림은 상기의 알고리즘을 다른 표준 네트워크상에서 실행한 결과를 나타내고 있습니다.이러한 결과는 해당 [36][39][41]출처에서 가져온 것이므로 개별적으로 처리해야 한다.

3노드에서 최대 [36]9노드까지의 서브그래프에 대한 Grochow-Kellis, mfinder, FANMOD, FPF 및 MODA 실행 시간.
Grochow-Kellis, FANMOD 및 G-Trie의 실행 시간(다른 5개의 [41]네트워크상의 3노드부터9노드까지).
네트워크 크기 센서스 원본 네트워크 랜덤 네트워크 평균 센서스
팬 모드 GK G-Trie 팬 모드 GK G-Trie
돌핀류 5 0.07 0.03 0.01 0.13 0.04 0.01
6 0.48 0.28 0.04 1.14 0.35 0.07
7 3.02 3.44 0.23 8.34 3.55 0.46
8 19.44 73.16 1.69 67.94 37.31 4.03
9 100.86 2984.22 6.98 493.98 366.79 24.84
회선 6 0.49 0.41 0.03 0.55 0.24 0.03
7 3.28 3.73 0.22 3.53 1.34 0.17
8 17.78 48.00 1.52 21.42 7.91 1.06
사회의 3 0.31 0.11 0.02 0.35 0.11 0.02
4 7.78 1.37 0.56 13.27 1.86 0.57
5 208.30 31.85 14.88 531.65 62.66 22.11
효모균 3 0.47 0.33 0.02 0.57 0.35 0.02
4 10.07 2.04 0.36 12.90 2.25 0.41
5 268.51 34.10 12.73 400.13 47.16 14.98
힘 3 0.51 1.46 0.00 0.91 1.37 0.01
4 1.38 4.34 0.02 3.01 4.40 0.03
5 4.68 16.95 0.10 12.38 17.54 0.14
6 20.36 95.58 0.55 67.65 92.74 0.88
7 101.04 765.91 3.36 408.15 630.65 5.17
3개의 다른 네트워크상의 3노드에서 [39]10노드까지의 서브그래프용 mfinder, FANMOD, Mavisto 및 Kavosh 실행시간.
사이즈 → 3 4 5 6 7 8 9 10
네트워크 ↓ 알고리즘 ↓
대장균 카보시 0.30 1.84 14.91 141.98 1374.0 13173.7 121110.3 1120560.1
팬 모드 0.81 2.53 15.71 132.24 1205.9 9256.6 - -
마비스토 13532 - - - - - - -
엠파인더 31.0 297 23671 - - - - -
전자의 카보시 0.08 0.36 8.02 11.39 77.22 422.6 2823.7 18037.5
팬 모드 0.53 1.06 4.34 24.24 160 967.99 - -
마비스토 210.0 1727 - - - - - -
엠파인더 7 14 109.8 2020.2 - - - -
사회의 카보시 0.04 0.23 1.63 10.48 69.43 415.66 2594.19 14611.23
팬 모드 0.46 0.84 3.07 17.63 117.43 845.93 - -
마비스토 393 1492 - - - - - -
엠파인더 12 49 798 181077 - - - -

알고리즘의 분류

표에서 보듯이 모티브 검출 알고리즘은 두 가지 일반적인 범주로 나눌 수 있다.정확한 카운트를 기반으로 하는 알고리즘과 통계적인 샘플링과 추정을 대신 사용하는 알고리즘이다.두 번째 그룹은 메인 네트워크에서 발생한 서브그래프의 모든 발생을 카운트하지 않기 때문에, 이 그룹에 속하는 알고리즘은 더 빠르지만 편향되고 비현실적인 결과를 낳을 수 있습니다.

다음 단계에서는 정확한 계수 알고리즘을 네트워크 중심 및 서브그래프 중심 방법으로 분류할 수 있습니다.첫 번째 클래스의 알고리즘은 주어진 크기의 모든 서브그래프에 대해 주어진 네트워크를 검색하는 반면, 두 번째 클래스에 속하는 알고리즘은 먼저 주어진 크기의 서로 다른 가능한 비동형 그래프를 생성한 후 생성된 각 서브그래프에 대해 개별적으로 네트워크를 탐색합니다.각 접근법에는 위에서 설명한 장점과 단점이 있습니다.

한편, 추정 방법은 앞에서 설명한 바와 같이 컬러 코딩 접근법을 사용할 수 있다.이 카테고리에 사용되는 다른 접근법은 일반적으로 열거 중에 일부 하위 그래프를 건너뛰고(예: FANMOD) 열거된 하위 그래프를 바탕으로 추정한다.

또한 이 표는 유도 또는 비유도 서브그래프뿐만 아니라 유도 또는 비유도 서브그래프에 알고리즘을 사용할 수 있는지 여부를 나타냅니다.자세한 내용은 제공된 웹 링크 또는 랩 주소를 참조하십시오.

모티브 검출 알고리즘 분류
계수법 근거 이름. 다이렉트/무다이렉트 유도/비유도
정확한 네트워크 중심 파인더 둘다요. 유도되다
ESU(FANMOD) 둘다요. 유도되다
카보시(Cyto Kavosh에서 사용) 둘다요. 유도되다
G-Tries 둘다요. 유도되다
PGD 무방향 유도되다
서브그래프 중심 FPF(마비스토) 둘다요. 유도되다
니모파인더 무방향 유도되다
그로초-켈리스 둘다요. 둘다요.
모다 둘다요. 둘다요.
견적/표본 추출 컬러 코딩 접근법 N. Alon 등의 알고리즘 무방향 비유발
기타 접근법 파인더 둘다요. 유도되다
ESU(FANMOD) 둘다요. 유도되다
알고리즘 설계자의 주소
알고리즘. 연구소 / 부서이름. 학과/학교 기관 주소. 이메일
파인더 우리알론의 그룹 분자세포생물학과 바이즈만 과학 연구소 이스라엘, 레호보트, 울프슨, Rm. 607 urialon (weizmann.ac.il )
FPF(마비스토) ---- ---- 라이프니츠 인스티튜트 퓌르 프란젠제네틱 und Kulturpflanzenforschung (IPK) 코렌스스트라셰 3, D-06466 슈타트 세일란트, OT 게터슬레벤, 독일 도이칠란트 shreibe (ipk-gatersleben.de )
ESU(FANMOD) 레흐르스툴 이론체 인포마티크 1세 인포마티크 연구소 프리드리히 쉴러 대학교 예나 에른스트아베플라츠 2, D-07743 예나, 독일 세바스찬wernicke (gmail.com )
니모파인더 ---- 컴퓨터 대학 싱가포르 국립 대학교 싱가포르 119077 첸진(comp.nus.edu.sg)
그로초-켈리스 CS 이론 그룹 및 복합 시스템 그룹 컴퓨터 사이언스 콜로라도 대학교 볼더 1111 엔지니어링 박사 ECOT 717, 430 UCB Boulder, CO 80309-0430 USA jgrochow는 colorado.edu에서 참조할 수 있습니다.
N. Alon 등의 알고리즘 순수 수학부 수리과학대학 텔아비브 대학교 텔아비브 69978(이스라엘) noga (post.tau.ac.il )
모다 시스템생물정보학연구소(LBB) 생화학 및 생물물리학 연구소(IBB) 테헤란 대학교 이란 테헤란, Enghelab Ave, Enghelab Square ibb.ut.ac.ir에서 아마수딘을 참조해 주세요.
카보시(Cyto Kavosh에서 사용) 시스템생물정보학연구소(LBB) 생화학 및 생물물리학 연구소(IBB) 테헤란 대학교 이란 테헤란, Enghelab Ave, Enghelab Square ibb.ut.ac.ir에서 아마수딘을 참조해 주세요.
G-Tries 고급 컴퓨팅 시스템 연구 센터 컴퓨터 사이언스 포르토 대학교 포르투갈 포르토, 루아 캄포 알레그레 1021/1055 pribeiro (dcc.fc.up.pt )
PGD 네트워크 학습 및 디스커버리 랩 컴퓨터 공학부 퍼듀 대학교 퍼듀 대학교, 305 N 대학교, 웨스트 라파예트, IN 47907 nkahmed@purdue.edu

잘 확립된 모티브와 그 기능

유전자 조절 네트워크의 네트워크 모티브를 이해하는 데 많은 실험 작업이 투입되었다.이러한 네트워크는 생물학적 신호에 반응하여 세포에서 발현되는 유전자를 조절한다.네트워크는 유전자가 노드라고 정의되며, 방향 가장자리는 다른 유전자에 의해 부호화된 전사인자(DNA와 결합하는 조절 단백질)에 의해 한 유전자의 제어를 나타낸다.따라서 네트워크 모티브는 서로의 전사율을 조절하는 유전자의 패턴이다.전사 네트워크를 분석하면 박테리아에서 인간에 이르기까지 다양한 생물에서 동일한 네트워크 모티브가 반복적으로 나타나는 것을 볼 수 있다.예를 들어 대장균과 효모의 전사 네트워크는 거의 전체 네트워크를 구성하는 세 가지 주요 모티브 패밀리로 구성됩니다.주연 가설 이후 규제 상호 작용의 작성 또는 제거 진화 시간 척도에 빠른 네트워크 주제 독자적으로 진화 과정에 의한 converging manner,[45][46]에서 유전자 게다가 change,[45][46][47]속도에 상대적인 선정된 것은 역학에 관한 실험들을 네트워크에 의해 만들어진다. 는 ce안에 살고 있는 모티브lls는 특징적인 동적 기능을 가지고 있음을 나타냅니다.이것은 네트워크 모티브가 유기체에 유익한 유전자 조절 네트워크에서 구성 요소 역할을 한다는 것을 암시한다.

전사 네트워크에서 공통 네트워크 모티브와 관련된 기능은 이론적으로나 실험적으로 여러 연구 프로젝트에 의해 탐색되고 입증되었다.다음으로 가장 일반적인 네트워크의 모티브와 그 관련 기능을 나타냅니다.

네거티브 오토 레귤레이션(NAR)

자동 규제 모티브의 개략도 표현

대장균에서 가장 간단하고 풍부한 네트워크 모티브 중 하나는 전사 인자(TF)가 자신의 전사를 억제하는 음성 자동 조절입니다.이 모티브는 두 가지 중요한 기능을 수행하는 것으로 나타났습니다.첫 번째 기능은 응답 가속입니다.NAR은 이론적으로나 실험적으로나 신호에 대한 응답 속도를 높이는 것으로 나타났다.이것은 합성 전사 네트워크에서[49] 처음 나타났고 나중에 대장균의 [50]SOS DNA 복구 시스템에서 자연스러운 맥락에서 나타났다.두 번째 기능은 확률적 소음에 대한 자동 조절 유전자 생성물 농도의 안정성을 증가시켜 서로 다른 [51][52][53]세포 간의 단백질 수준 변화를 감소시키는 것이다.

포지티브 오토레귤레이션(PAR)

포지티브 오토 레귤레이션(PAR)은, 문자 변환 팩터가 독자적인 생산 레이트를 높였을 때에 발생합니다.NAR 모티브와는 반대로, 이 모티브는 단순한 [54]규제에 비해 응답 시간이 느립니다.강한 PAR의 경우 모티브는 세포 [55]집단에서 단백질 수준의 바이모달 분포를 초래할 수 있습니다.

피드 포워드 루프(FFL)

피드포워드 모티브의 개략도 표현

이 모티브는 많은 유전자 시스템과 유기체에서 흔히 발견된다.모티브는 3개의 유전자와 3개의 조절 상호작용으로 구성됩니다.표적 유전자 C는 2개의 TF A와 B에 의해 조절되며, 또한 TF B도 TF A에 의해 조절된다. 각각의 조절 상호작용이 양수이거나 음수일 수 있기 때문에 FFL [56]모티브에는 8가지 유형이 있을 수 있다.이들 8종 중 2종류인 코히런트형 1FFL(모든 상호작용이 양)과 비코히런트형 1FFL(I1-FFL)(A는 C를 활성화하고 C를 억제하는 B도 활성화함)은 대장균 및 효모의 전사 네트워크에서 훨씬 더 자주 발견된다.[56][57]회로의 구조와 더불어 A와 B로부터의 신호가 C 프로모터에 의해 집적되는 방법도 고려해야 합니다.대부분의 경우 FFL은 AND 게이트(A와 B는 C 활성화에 필요) 또는 OR 게이트(A 또는 B는 C 활성화에 충분)이지만 다른 입력 기능도 가능합니다.

코히런트 타입 1 FFL(C1-FFL)

AND 게이트가 있는 C1-FFL은 이론적으로나 실험적으로나[58] 대장균의 아라비노스 시스템과 함께 '신호 민감 지연' 요소와 지속성 검출기의 기능을 가진 것으로 나타났다.즉, 이 모티브는 짧은 신호의 펄스는 응답을 생성하지 않지만 지속적 신호는 짧은 지연 후에 응답을 생성하는 펄스 필터링을 제공할 수 있습니다.지속 펄스가 종료될 때 출력이 빠르게 차단됩니다.대장균 [59]편모계에서 입증되었듯이 반응이 빠르고 차단이 지연된 섬 게이트의 경우 반대의 동작이 나타난다.유전자 조절 네트워크에서 C1-FFLs의 de novo 진화는 이상적인 단신호 펄스를 걸러내는 선택에 따라 계산적으로 입증되었지만, 이상화되지 않은 소음의 경우 다른 위상을 가진 피드포워드 조절의 역학 기반 시스템이 [60]선호되었다.

일관성이 없는 타입 1 FFL(I1-FFL)

I1-FFL은 펄스 발생기 및 응답 가속기입니다.I1-FFL의 두 신호 경로는 한쪽 경로가 Z를 활성화하고 다른 한쪽 경로가 Z를 억제하는 반대 방향으로 작용한다.억제가 완료되면 펄스 형태의 역학이 발생합니다.또한 I1-FFL이 NAR 모티브와 유사한 방식으로 응답 가속기 역할을 할 수 있다는 것이 실험적으로 입증되었다.차이점은 I1-FFL이 반드시 전사인자 [61]유전자가 아니라 어떤 유전자의 반응 속도를 높일 수 있다는 것이다.I1-FFL 네트워크 모티브에 추가 기능이 할당되었습니다.I1-FFL이 합성 시스템과 네이티브 [63]시스템 모두에서 비단조 입력 함수를 생성할 수 있다는 것이 이론적으로나 실험적으로나 증명되었습니다.마지막으로 유전자 생성물의 일관되지 않은 피드포워드 제어를 포함한 발현단위는 DNA 템플릿의 양에 대한 적응을 제공하며 구성촉진제의 [64]단순한 조합보다 우수할 수 있다.피드포워드 조절은 음성 피드백보다 더 나은 적응을 보였으며, RNA 간섭에 기반한 회로가 DNA 템플릿 [64]양의 변동에 가장 강력했다.

멀티 출력 FFL

경우에 따라서는 동일한 조절기 X와 Y가 동일한 계통의 여러 Z 유전자를 조절합니다.상호작용의 강도를 조절함으로써 이 모티프는 유전자 활성화의 시간적 순서를 결정하는 것으로 나타났다.이는 대장균 [65]편모계에서 실험적으로 입증되었다.

싱글 입력 모듈(SIM)

이 모티브는 단일 조절기가 추가적인 조절 없이 일련의 유전자를 조절할 때 발생합니다.이것은 유전자가 협력적으로 특정 기능을 수행하고 있기 때문에 항상 동기화된 방식으로 활성화되어야 할 때 유용합니다.상호작용의 강도를 조절함으로써 [66]조절하는 유전자의 시간적 발현 프로그램을 만들 수 있다.

문헌에서 다중 입력 모듈(MIM)은 SIM의 일반화로서 등장했습니다.그러나 SIM과 MIM의 정확한 정의는 불일치의 원인이 되어 왔습니다.생물학적 네트워크와 이들을 열거하기 위한 알고리즘, 특히 SIM, MIM 및 Bi-Fan(2x2 [67]MIM)에서 표준 모티브에 대한 직교 정의를 제공하려는 시도가 있다.

고밀도 중복 규제(DOR)

이 모티브는 여러 조절자가 다양한 조절 조합을 가진 유전자 세트를 조합적으로 제어하는 경우에 발생한다.이러한 모티브는 탄소 활용, 혐기성 성장, 스트레스 반응 [17][22]등과 같은 다양한 시스템의 대장균에서 발견되었습니다.이 모티브의 기능을 더 잘 이해하기 위해서는 여러 입력이 유전자에 의해 통합되는 방법에 대한 더 많은 정보를 얻어야 한다.카플란 [68]등대장균의 당 이용 유전자의 입력 기능을 지도화하여 다양한 형태를 보여주고 있습니다.

액티비티 모티브

네트워크 모티프의 흥미로운 일반화는 네트워크 내의 노드와 엣지에 정량적 피쳐가 주석을 달았을 때 찾을 수 있는 발생 패턴에 대한 활동 모티브입니다.예를 들어, 대사 경로의 가장자리에 대응하는 유전자 발현 크기 또는 타이밍이 주석을 붙일 경우, 기초 네트워크 [69]구조가 주어지면 일부 패턴이 과잉으로 발생한다.

비판

위상 하위 구조의 보존 뒤에 있는 가정(때로는 더 암묵적이지 않은 가정)은 특정 기능적으로 중요하다는 것이다.이 가정은 최근에 의문이 제기되었다.일부 저자는 모티브가 바이팬 모티브와 마찬가지로 네트워크 컨텍스트에 따라 다양함을 나타낼 수 있으므로 [70]모티브의 구조가 반드시 기능을 결정하는 것은 아니라고 주장한다.네트워크 구조가 항상 기능을 나타내는 것은 아닙니다.이것은, 예를 들면 Sin 오퍼론을 [71]참조해 주세요.

모티브 함수의 분석은 대부분 모티브가 단독으로 동작하는 것을 보고 실시합니다.최근의 연구는 네트워크[72] 컨텍스트, 즉 모티브와 네트워크의 나머지 부분과의 접속이 로컬 구조에서만 기능에 대한 추론을 도출하기에는 너무 중요하다는 좋은 증거를 제시합니다.인용된 논문은 관찰된 데이터에 대한 비판과 대체 설명도 검토합니다.단일 모티브 모듈이 네트워크의 글로벌 다이내믹스에 미치는 영향에 대한 분석을 [73]연구한다.그러나 또 다른 최근의 연구는 생물학적 네트워크의 특정 토폴로지 특성이 자연스럽게 표준 모티브의 공통적인 모습을 만들어 낸다는 것을 시사하고, 따라서 발생 빈도가 [74][75]모티브의 구조가 네트워크 운영에 대한 기능적 기여를 위해 선택된다는 합리적인 증거인지 의문을 제기한다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Masoudi-Nejad A, Schreiber F, Razaghi MK Z (2012). "Building Blocks of Biological Networks: A Review on Major Network Motif Discovery Algorithms". IET Systems Biology. 6 (5): 164–74. doi:10.1049/iet-syb.2011.0011. PMID 23101871.
  2. ^ Diestel, Reinhard (2005). Graph theory (3rd ed.). Berlin: Springer. ISBN 9783540261827.
  3. ^ a b c Milo R, Shen-Orr SS, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–827. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
  4. ^ Albert R, Barabási AL (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–49. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47. S2CID 60545.
  5. ^ a b Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U (2004). "Superfamilies of designed and evolved networks". Science. 303 (5663): 1538–1542. Bibcode:2004Sci...303.1538M. doi:10.1126/science.1089167. PMID 15001784. S2CID 14760882.
  6. ^ a b Schwöbbermeyer, H (2008). "Network Motifs". In Junker BH, Schreiber F (ed.). Analysis of Biological Networks. Hoboken, New Jersey: John Wiley & Sons. pp. 85–108.
  7. ^ Bornholdt, S; Schuster, HG (2003). "Handbook of graphs and networks : from the genome to the Internet". Handbook of Graphs and Networks: From the Genome to the Internet. p. 417. Bibcode:2003hgnf.book.....B.
  8. ^ a b c Ciriello G, Guerra C (2008). "A review on models and algorithms for motif discovery in protein-protein interaction networks". Briefings in Functional Genomics and Proteomics. 7 (2): 147–156. doi:10.1093/bfgp/eln015. PMID 18443014.
  9. ^ a b c d e f Kashtan N, Itzkovitz S, Milo R, Alon U (2004). "Efficient sampling algorithm for estimating sub-graph concentrations and detecting network motifs". Bioinformatics. 20 (11): 1746–1758. doi:10.1093/bioinformatics/bth163. PMID 15001476.
  10. ^ a b c d e f Wernicke S (2006). "Efficient detection of network motifs". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 3 (4): 347–359. CiteSeerX 10.1.1.304.2576. doi:10.1109/tcbb.2006.51. PMID 17085844. S2CID 6188339.
  11. ^ Picard F, Daudin JJ, Schbath S, Robin S (2005). "Assessing the Exceptionality of Network Motifs". J. Comp. Bio. 15 (1): 1–20. CiteSeerX 10.1.1.475.4300. doi:10.1089/cmb.2007.0137. PMID 18257674.
  12. ^ a b c Schreiber F, Schwöbbermeyer H (2005). "Frequency concepts and pattern detection for the analysis of motifs in networks". Transactions on Computational Systems Biology III. Lecture Notes in Computer Science. Vol. 3737. pp. 89–104. CiteSeerX 10.1.1.73.1130. doi:10.1007/11599128_7. ISBN 978-3-540-30883-6.
  13. ^ Holland, P. W., & Leinhardt, S. (1974년)소셜 네트워크의 로컬 구조에 대한 통계 분석.국립경제조사국 업무용지 제44호
  14. ^ Holland, P., & Leinhardt, S.(1975).로컬 통계 분석.소셜 네트워크의 구조사회학적 방법론, David Heise, ed.샌프란시스코:호세바스
  15. ^ Holland, P. W., & Leinhardt, S. (1976년)소셜 네트워크의 로컬 구조.사회학적 방법론, 7, 1~45
  16. ^ Holland, P. W., & Leinhardt, S.(1977년).사회계량학 데이터의 구조를 검출하는 방법.소셜 네트워크 (p. 411-432).학술용 프레스
  17. ^ a b c Shen-Orr SS, Milo R, Mangan S, Alon U (May 2002). "Network motifs in the transcriptional regulation network of Escherichia coli". Nat. Genet. 31 (1): 64–8. doi:10.1038/ng881. PMID 11967538. S2CID 2180121.
  18. ^ Eichenberger P, Fujita M, Jensen ST, et al. (October 2004). "The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis". PLOS Biology. 2 (10): e328. doi:10.1371/journal.pbio.0020328. PMC 517825. PMID 15383836. open access
  19. ^ Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (October 2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–7. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
  20. ^ Lee TI, Rinaldi NJ, Robert F, et al. (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584. S2CID 4841222.
  21. ^ Odom DT, Zizlsperger N, Gordon DB, et al. (February 2004). "Control of pancreas and liver gene expression by HNF transcription factors". Science. 303 (5662): 1378–81. Bibcode:2004Sci...303.1378O. doi:10.1126/science.1089769. PMC 3012624. PMID 14988562.
  22. ^ a b Boyer LA, Lee TI, Cole MF, et al. (September 2005). "Core transcriptional regulatory circuitry in human embryonic stem cells". Cell. 122 (6): 947–56. doi:10.1016/j.cell.2005.08.020. PMC 3006442. PMID 16153702.
  23. ^ Iranfar N, Fuller D, Loomis WF (February 2006). "Transcriptional regulation of post-aggregation genes in Dictyostelium by a feed-forward loop involving GBF and LagC". Dev. Biol. 290 (2): 460–9. doi:10.1016/j.ydbio.2005.11.035. PMID 16386729.
  24. ^ Ma'ayan A, Jenkins SL, Neves S, et al. (August 2005). "Formation of regulatory patterns during signal propagation in a Mammalian cellular network". Science. 309 (5737): 1078–83. Bibcode:2005Sci...309.1078M. doi:10.1126/science.1108876. PMC 3032439. PMID 16099987.
  25. ^ Ptacek J, Devgan G, Michaud G, et al. (December 2005). "Global analysis of protein phosphorylation in yeast" (PDF). Nature (Submitted manuscript). 438 (7068): 679–84. Bibcode:2005Natur.438..679P. doi:10.1038/nature04187. PMID 16319894. S2CID 4332381.
  26. ^ "Acc-Motif: Accelerated Motif Detection".
  27. ^ Schreiber F, Schwobbermeyer H (2005). "MAVisto: a tool for the exploration of network motifs". Bioinformatics. 21 (17): 3572–3574. doi:10.1093/bioinformatics/bti556. PMID 16020473.
  28. ^ a b c McKay BD (1981). "Practical graph isomorphism". Congressus Numerantium. 30: 45–87. arXiv:1301.1493. Bibcode:2013arXiv1301.1493M.
  29. ^ a b c McKay BD (1998). "Isomorph-free exhaustive generation". Journal of Algorithms. 26 (2): 306–324. doi:10.1006/jagm.1997.0898.
  30. ^ a b Chen J, Hsu W, Li Lee M, et al. (2006). NeMoFinder: dissecting genome-wide protein-protein interactions with meso-scale network motifs. the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. Philadelphia, Pennsylvania, USA. pp. 106–115.
  31. ^ Huan J, Wang W, Prins J, et al. (2004). SPIN: mining maximal frequent sub-graphs from graph databases. the 10th ACM SIGKDD international conference on Knowledge discovery and data mining. pp. 581–586.
  32. ^ Uetz P, Giot L, Cagney G, et al. (2000). "A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae". Nature. 403 (6770): 623–627. Bibcode:2000Natur.403..623U. doi:10.1038/35001009. PMID 10688190. S2CID 4352495.
  33. ^ a b c d Grochow JA, Kellis M (2007). Network Motif Discovery Using Sub-graph Enumeration and Symmetry-Breaking (PDF). RECOMB. pp. 92–106. doi:10.1007/978-3-540-71681-5_7.
  34. ^ a b Grochow JA (2006). On the structure and evolution of protein interaction networks (PDF). Thesis M. Eng., Massachusetts Institute of Technology, Dept. of Electrical Engineering and Computer Science.
  35. ^ a b c Alon N; Dao P; Hajirasouliha I; Hormozdiari F; Sahinalp S.C (2008). "Biomolecular network motif counting and discovery by color coding". Bioinformatics. 24 (13): i241–i249. doi:10.1093/bioinformatics/btn163. PMC 2718641. PMID 18586721.
  36. ^ a b c d e Omidi S, Schreiber F, Masoudi-Nejad A (2009). "MODA: an efficient algorithm for network motif discovery in biological networks". Genes Genet Syst. 84 (5): 385–395. doi:10.1266/ggs.84.385. PMID 20154426.
  37. ^ Barabasi AL, Albert R (1999). "Emergence of scaling in random networks". Science. 286 (5439): 509–512. arXiv:cond-mat/9910332. Bibcode:1999Sci...286..509B. doi:10.1126/science.286.5439.509. PMID 10521342. S2CID 524106.
  38. ^ Vázquez A, Dobrin R, Sergi D, et al. (2004). "The topological relationship between the large-scale attributes and local interaction patterns of complex networks". PNAS. 101 (52): 17940–17945. arXiv:cond-mat/0408431. Bibcode:2004PNAS..10117940V. doi:10.1073/pnas.0406024101. PMC 539752. PMID 15598746.
  39. ^ a b c d Kashani ZR, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A (2009). "Kavosh: a new algorithm for finding network motifs". BMC Bioinformatics. 10 (318): 318. doi:10.1186/1471-2105-10-318. PMC 2765973. PMID 19799800. open access
  40. ^ Ali Masoudi-Nejad; Mitra Anasariola; Ali Salehzadeh-Yazdi; Sahand Khakabimamaghani (2012). "CytoKavosh: a Cytoscape Plug-in for Finding Network Motifs in Large Biological Networks". PLOS ONE. 7 (8): e43287. Bibcode:2012PLoSO...743287M. doi:10.1371/journal.pone.0043287. PMC 3430699. PMID 22952659. open access
  41. ^ a b c d Ribeiro P, Silva F (2010). G-Tries: an efficient data structure for discovering network motifs. ACM 25th Symposium On Applied Computing - Bioinformatics Track. Sierre, Switzerland. pp. 1559–1566.
  42. ^ Mbadiwe, Somadina; Kim, Wooyoung (November 2017). "ParaMODA: Improving motif-centric subgraph pattern search in PPI networks". 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM): 1723–1730. doi:10.1109/BIBM.2017.8217920. ISBN 978-1-5090-3050-7. S2CID 5806529.
  43. ^ "NemoMap: Improved Motif-centric Network Motif Discovery Algorithm". Advances in Science, Technology and Engineering Systems Journal. 2018. Retrieved 2020-09-11.
  44. ^ Patra, Sabyasachi; Mohapatra, Anjali (2020). "Review of tools and algorithms for network motif discovery in biological networks". IET Systems Biology. 14 (4): 171–189. doi:10.1049/iet-syb.2020.0004. ISSN 1751-8849. PMC 8687426. PMID 32737276.
  45. ^ a b Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA (June 2004). "Structure and evolution of transcriptional regulatory networks". Current Opinion in Structural Biology. 14 (3): 283–91. CiteSeerX 10.1.1.471.9692. doi:10.1016/j.sbi.2004.05.004. PMID 15193307.
  46. ^ a b Conant GC, Wagner A (July 2003). "Convergent evolution of gene circuits". Nat. Genet. 34 (3): 264–6. doi:10.1038/ng1181. PMID 12819781. S2CID 959172.
  47. ^ Dekel E, Alon U (July 2005). "Optimality and evolutionary tuning of the expression level of a protein". Nature. 436 (7050): 588–92. Bibcode:2005Natur.436..588D. doi:10.1038/nature03842. PMID 16049495. S2CID 2528841.
  48. ^ Zabet NR (September 2011). "Negative feedback and physical limits of genes". Journal of Theoretical Biology. 284 (1): 82–91. arXiv:1408.1869. Bibcode:2011JThBi.284...82Z. CiteSeerX 10.1.1.759.5418. doi:10.1016/j.jtbi.2011.06.021. PMID 21723295. S2CID 14274912.
  49. ^ Rosenfeld N, Elowitz MB, Alon U (November 2002). "Negative autoregulation speeds the response times of transcription networks". J. Mol. Biol. 323 (5): 785–93. CiteSeerX 10.1.1.126.2604. doi:10.1016/S0022-2836(02)00994-4. PMID 12417193.
  50. ^ Camas FM, Blázquez J, Poyatos JF (August 2006). "Autogenous and nonautogenous control of response in a genetic network". Proc. Natl. Acad. Sci. U.S.A. 103 (34): 12718–23. Bibcode:2006PNAS..10312718C. doi:10.1073/pnas.0602119103. PMC 1568915. PMID 16908855.
  51. ^ Becskei A, Serrano L (June 2000). "Engineering stability in gene networks by autoregulation". Nature. 405 (6786): 590–3. Bibcode:2000Natur.405..590B. doi:10.1038/35014651. PMID 10850721. S2CID 4407358.
  52. ^ Dublanche Y, Michalodimitrakis K, Kümmerer N, Foglierini M, Serrano L (2006). "Noise in transcription negative feedback loops: simulation and experimental analysis". Mol. Syst. Biol. 2 (1): 41. doi:10.1038/msb4100081. PMC 1681513. PMID 16883354.
  53. ^ Shimoga V, White J, Li Y, Sontag E, Bleris L (2013). "Synthetic mammalian transgene negative autoregulation". Mol. Syst. Biol. 9: 670. doi:10.1038/msb.2013.27. PMC 3964311. PMID 23736683.
  54. ^ Maeda YT, Sano M (June 2006). "Regulatory dynamics of synthetic gene networks with positive feedback". J. Mol. Biol. 359 (4): 1107–24. doi:10.1016/j.jmb.2006.03.064. PMID 16701695.
  55. ^ Becskei A, Séraphin B, Serrano L (May 2001). "Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion". EMBO J. 20 (10): 2528–35. doi:10.1093/emboj/20.10.2528. PMC 125456. PMID 11350942.
  56. ^ a b c Mangan S, Alon U (October 2003). "Structure and function of the feed-forward loop network motif". Proc. Natl. Acad. Sci. U.S.A. 100 (21): 11980–5. Bibcode:2003PNAS..10011980M. doi:10.1073/pnas.2133841100. PMC 218699. PMID 14530388.
  57. ^ Ma HW, Kumar B, Ditges U, Gunzer F, Buer J, Zeng AP (2004). "An extended transcriptional regulatory network of Escherichia coli and analysis of its hierarchical structure and network motifs". Nucleic Acids Res. 32 (22): 6643–9. doi:10.1093/nar/gkh1009. PMC 545451. PMID 15604458.
  58. ^ Mangan S, Zaslaver A, Alon U (November 2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks". J. Mol. Biol. 334 (2): 197–204. CiteSeerX 10.1.1.110.4629. doi:10.1016/j.jmb.2003.09.049. PMID 14607112.
  59. ^ Kalir S, Mangan S, Alon U (2005). "A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli". Mol. Syst. Biol. 1 (1): E1–E6. doi:10.1038/msb4100010. PMC 1681456. PMID 16729041.
  60. ^ Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. Bibcode:2019NatCo..10.2418X. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.
  61. ^ Mangan S, Itzkovitz S, Zaslaver A, Alon U (March 2006). "The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli". J. Mol. Biol. 356 (5): 1073–81. CiteSeerX 10.1.1.184.8360. doi:10.1016/j.jmb.2005.12.003. PMID 16406067.
  62. ^ Entus R, Aufderheide B, Sauro HM (August 2007). "Design and implementation of three incoherent feed-forward motif based biological concentration sensors". Syst Synth Biol. 1 (3): 119–28. doi:10.1007/s11693-007-9008-6. PMC 2398716. PMID 19003446.
  63. ^ Kaplan S, Bren A, Dekel E, Alon U (2008). "The incoherent feed-forward loop can generate non-monotonic input functions for genes". Mol. Syst. Biol. 4 (1): 203. doi:10.1038/msb.2008.43. PMC 2516365. PMID 18628744.
  64. ^ a b Bleris L, Xie Z, Glass D, Adadey A, Sontag E, Benenson Y (2011). "Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template". Mol. Syst. Biol. 7 (1): 519. doi:10.1038/msb.2011.49. PMC 3202791. PMID 21811230.
  65. ^ Kalir S, McClure J, Pabbaraju K, et al. (June 2001). "Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria". Science. 292 (5524): 2080–3. doi:10.1126/science.1058758. PMID 11408658. S2CID 14396458.
  66. ^ Zaslaver A, Mayo AE, Rosenberg R, et al. (May 2004). "Just-in-time transcription program in metabolic pathways". Nat. Genet. 36 (5): 486–91. doi:10.1038/ng1348. PMID 15107854.
  67. ^ Konagurthu AS, Lesk AM (2008). "Single and Multiple Input Modules in regulatory networks". Proteins. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061. S2CID 35715566.
  68. ^ Kaplan S, Bren A, Zaslaver A, Dekel E, Alon U (March 2008). "Diverse two-dimensional input functions control bacterial sugar genes". Mol. Cell. 29 (6): 786–92. doi:10.1016/j.molcel.2008.01.021. PMC 2366073. PMID 18374652.
  69. ^ Chechik G, Oh E, Rando O, Weissman J, Regev A, Koller D (November 2008). "Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network". Nat. Biotechnol. 26 (11): 1251–9. doi:10.1038/nbt.1499. PMC 2651818. PMID 18953355.
  70. ^ Ingram PJ, Stumpf MP, Stark J (2006). "Network motifs: structure does not determine function". BMC Genomics. 7: 108. doi:10.1186/1471-2164-7-108. PMC 1488845. PMID 16677373. open access
  71. ^ Voigt CA, Wolf DM, Arkin AP (March 2005). "The Bacillus subtilis sin operon: an evolvable network motif". Genetics. 169 (3): 1187–202. doi:10.1534/genetics.104.031955. PMC 1449569. PMID 15466432.
  72. ^ Knabe JF, Nehaniv CL, Schilstra MJ (2008). "Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies". BioSystems. 94 (1–2): 68–74. doi:10.1016/j.biosystems.2008.05.012. PMID 18611431.
  73. ^ Taylor D, Restrepo JG (2011). "Network connectivity during mergers and growth: Optimizing the addition of a module". Physical Review E. 83 (6): 66112. arXiv:1102.4876. Bibcode:2011PhRvE..83f6112T. doi:10.1103/PhysRevE.83.066112. PMID 21797446. S2CID 415932.
  74. ^ Konagurthu, Arun S.; Lesk, Arthur M. (23 April 2008). "Single and multiple input modules in regulatory networks". Proteins: Structure, Function, and Bioinformatics. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061. S2CID 35715566.
  75. ^ Konagurthu AS, Lesk AM (2008). "On the origin of distribution patterns of motifs in biological networks". BMC Syst Biol. 2: 73. doi:10.1186/1752-0509-2-73. PMC 2538512. PMID 18700017. open access

외부 링크