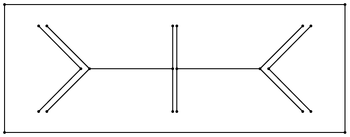
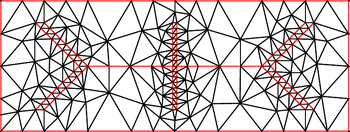
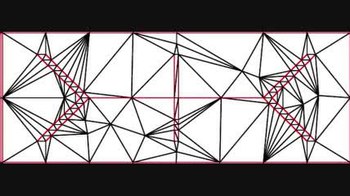
딜라우나이 정제

Delaunay refinement

메쉬 생성에서 델로나이 미세화는 메싱 애플리케이션의 품질 요건을 충족하기 위해 증분 입력의 델로나이 삼각측량 또는 제약된 델로나이 삼각측량을 유발하는 방식으로 메쉬 생성에 스테이너 포인트를 추가하는 원리에 근거한 알고리즘이다.델라우나이 정제 방법에는 츄와 루퍼트의 방법이 포함된다.

츄의 두 번째 알고리즘

Mesh generated with Chew's second algorithm text
미시간 호수의 메쉬는 트라이앵글 패키지에 구현된 츄의 두 번째 알고리즘을 사용한다.

츄의 두 번째 알고리즘은 조각으로 된 선형 시스템(PLS)을 취하여 삼각형의 최소 각도로 품질이 정의되는 품질 삼각형에만 대한 제한된 델로나이 삼각측량을 반환한다.L. Paul Chuc이 3차원 공간에 내장한 표면을 메싱하기 위해 개발한 츄의 두 번째 알고리즘은 특정 경우 Rupert의 알고리즘에 비해 실용적 이점이 있어 2차원 메쉬 발생기로 채택되었으며, 자유롭게 이용할 수 있는 Triangle 패키지에서 구현되는 기본 품질 메쉬 생성기다.[1][2]츄의 두 번째 알고리즘은 최소 각도가 약 28.6도인 국소 피쳐 크기 등급의 메쉬를 종료하고 생산할 수 있도록 보장된다.[3]

알고리즘은 입력 정점의 제한된 Delaunay 삼각측정으로 시작한다.각 단계에서 품질이 좋지 않은 삼각형의 원곡선을 삼각측량 안에 삽입하되, 예외는 다음과 같다.품질이 좋지 않은 삼각형으로서 곡선이 입력 세그먼트의 반대편에 있는 경우 세그먼트의 중간점이 삽입된다.또한 원래 세그먼트의 직경 볼 내부에 이전에 삽입된 원주형(분할되기 전)은 삼각측량에서 제거된다.질이 나쁜 삼각형이 존재하지 않을 때까지 할로우센터 삽입을 반복한다.

루퍼트 알고리즘

Ruppert's Algorithm input
입력 평면 직선 그래프
Output conforming Delaunay triangulation
Delaunay 삼각 측정에 적합한 출력
Ruppert의 알고리즘 예제

Ruppert의 알고리즘은 평면 직선 그래프(또는 조각으로 된 선형 시스템 2개보다 높은 차원)를 취하여 품질 삼각형에만 해당하는 Delaunay 삼각측량을 반환한다.삼각형은 규정된 임계값보다 큰 최단 에지 대비 원곡선 비율이 있는 경우 품질이 좋지 않은 것으로 간주된다.1990년대 초 짐 루퍼트에 의해 발견된 [4]"Ruppert의 2차원 품질 메쉬 생성 알고리즘은 아마도 이론적으로 보장된 최초의 메싱 알고리즘일 것이다.[5]

동기

컴퓨터 유체 역학 같은 컴퓨터 시뮬레이션을 할 때는 날개 부분의 2D 윤곽과 같은 모델부터 시작한다.2D 유한요소법에 대한 입력은 모든 공간을 채우는 삼각형의 형태로, 그리고 각 삼각형은 하나의 재료로 채워져야 한다 – 이 예에서, "공기" 또는 "날개".길고 마른 삼각형은 정확하게 시뮬레이션할 수 없다.시뮬레이션 시간은 일반적으로 삼각형의 수에 비례하므로 삼각형의 수를 최소화하는 동시에 합리적으로 정확한 결과를 제공할 수 있는 충분한 삼각형을 사용하는 것이 보통 비정형 그리드를 사용하는 방법이다.컴퓨터는 루퍼트의 알고리즘(또는 비슷한 메싱 알고리즘)을 사용하여 다각형 모델을 유한요소법에 적합한 삼각형으로 변환한다.

루퍼트 알고리즘의 중간 삼각측량

알고리즘.

알고리즘은 입력 정점의 Delaunay 삼각측량에서 시작하여 두 개의 주요 연산으로 구성된다.

  • 직경이 비어 있지 않은 세그먼트의 중간점은 삼각 측정에 삽입된다.
  • 이 곡선이 일부 세그먼트의 직경 원 안에 있지 않는 한, 품질이 좋지 않은 삼각형의 곡선은 삼각 측정에 삽입된다.이 경우 잠식된 세그먼트가 대신 분할된다.

이러한 작업은 저품질 삼각형이 존재하지 않고 모든 세그먼트가 잠식되지 않을 때까지 반복된다.

가성음
함수 Ruppert(점, 세그먼트, 임계값)는 T :=DelaunayTriangulation(점) Q := 침해된 세그먼트와 불량한 품질 삼각형의 집합인 반면 Q는 비어 있지 않은 경우: // Q가 세그먼트 s를 포함할 경우 주 루프: s의 중간점을 T에 삽입하고, Q는 낮은 품질의 삼각형 t를 포함할 경우:t의 nter는 세그먼트 s를 잠식한다: Q에 s를 추가한다. 그렇지 않으면: T의 원곡선을 T 엔드에 삽입한다. 업데이트 Q가 종료되면 T 엔드에 삽입하고 T end Ruppert를 반환한다.

실용적 사용법

수정하지 않으면 Ruppert의 알고리즘은 비급성 입력과 약 20.7도 미만의 불량 품질 임계값에 대한 품질 망사를 종료하고 생성하도록 보장된다.이러한 제한을 완화하기 위해 다양한 작은 개선들이 이루어졌다.작은 입력 각도에 가까운 품질 요건을 완화함으로써 알고리즘을 확장하여 모든 직선 입력을 처리할 수 있다.[6]곡선 입력을 유사한 기법을 사용하여 메싱할 수도 있다.[7]루퍼트의 알고리즘은 자연스럽게 3차원까지 확장할 수 있지만, 슬리버형 사면체 때문에 출력 보장이 다소 약하다.

자유롭게 이용할 수 있는 트라이앵글 패키지에서 2차원 Ruppert 알고리즘의 확장이 구현된다.이 패키지에 포함된 두 가지 종류의 Ruppert 알고리즘은 약 26.5도의 낮은 품질 임계값에 대해 종료가 보장된다.[8]실제로 이러한 알고리즘은 30도 이상의 낮은 품질 임계값에 대해 성공적이다.그러나 알고리즘이 29.06도보다 큰 임계값으로 장애를 일으키는 예는 알려져 있다.[9]

참고 항목

참조

  1. ^ Chew, L. Paul (1993). "Guaranteed-quality mesh generation for curved surfaces". Proceedings of the Ninth Annual Symposium on Computational Geometry. pp. 274–280.
  2. ^ Shewchuk, Jonathan (2002). "Delaunay refinement algorithms for triangular mesh generation". Computational Geometry: Theory and Applications. 22 (1–3): 21–74. doi:10.1016/s0925-7721(01)00047-5.
  3. ^ Rand, Alexander (2011). "Where and How Chew's Second Delaunay Refinement Algorithm Works" (PDF). Proceedings of the 23rd Canadian Conference on Computational Geometry. pp. 157–162.
  4. ^ Ruppert, Jim (1995). "A Delaunay refinement algorithm for quality 2-dimensional mesh generation". Journal of Algorithms. 18 (3): 548–585. doi:10.1006/jagm.1995.1021.
  5. ^ Shewchuk, Jonathan (12 August 1996). "Ruppert's Delaunay Refinement Algorithm". Retrieved 28 December 2018.
  6. ^ Miller, Gary; Pav, Steven; Walkington, Noel (2005). "When and why Delaunay refinement algorithms work". International Journal of Computational Geometry and Applications. 15 (1): 25–54. doi:10.1142/S0218195905001592.
  7. ^ Pav, Steven; Walkington, Noel (2005). Delaunay refinement by corner lopping. Proceedings of the 14th International Meshing Roundtable. pp. 165–181.
  8. ^ Shewchuk, Jonathan (2002). "Delaunay refinement algorithms for triangular mesh generation". Computational Geometry: Theory and Applications. 22 (1–3): 21–74. doi:10.1016/s0925-7721(01)00047-5.
  9. ^ Rand, Alexander (2011). "Improved Examples of Non-Termination for Ruppert's Algorithm". arXiv:1103.3903 [cs.CG]..

추가 읽기