짹짹

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Chirp" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2010년 8월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

짹짹거리는 주파수가 시간에 따라 증가하거나 감소하는 신호다. 어떤 출처에서는 짹짹이라는 용어가 스위프 신호와 호환되게 사용된다.^[1] 그것은 일반적으로 음파 탐지, 레이더 및 레이저 시스템에 적용되며 확산-스펙트럼 통신과 같은 다른 용도에 적용된다(처프 확산 스펙트럼 참조). 이 신호 유형은 생물학적으로 영감을 받아 분산(파형 성분의 주파수 및 전파 속도 간 비선형 의존성)에 의한 현상으로 발생한다. 그것은 보통 전파 채널의 일부가 될 수 있는 일치 필터를 사용하여 보상된다. 그러나 구체적인 성능 측정에 따라 레이더와 통신 모두 더 나은 기법이 있다. 레이더와 우주에서 사용되었기 때문에 통신 표준에도 채택되었다. 자동차용 레이더 어플리케이션의 경우 보통 LFMW(Linear Frequency Modulated Waveform)라고 부른다.

확산 스펙트럼 사용에서 표면 음향파(SAW) 장치는 처림 신호를 생성하고 격하시키는 데 사용된다. 광학에서 울트라쇼트 레이저 펄스는 또한 짹짹거리는 소리를 나타내며, 광전달 시스템에서는 물질의 분산 특성과 상호 작용하여 신호가 전파됨에 따라 총 펄스 분산을 증가시키거나 감소시킨다. 그 이름은 새가 지저귀는 소리를 가리키는 것이다. 새의 발성을 보라.

정의들

여기서의 기본적인 정의는 공통물리 수량 위치(상), 속도(사각 속도), 가속도(치피니티)로 해석된다. 파형이 다음과 같이 정의된 경우:

$\displaystyle x(t)=\sin \left(\phi(t)\오른쪽)$

즉석 각도 주파수 Ω은 위상의 첫 번째 파생상품에서 주어진 위상 속도로 정의되며, 순간 일반 주파수 f는 정상화된 버전이다.

${\displaystyle \omega(t)={\frac {d\pi(t)}{dt},\,f(t)={\frac {\omega(t)}{2\pi }}}}}$

마지막으로, 순간 각 치르피티 γ은 순간 단계의 두 번째 파생물 또는 순간 각진수의 첫 번째 파생물로 정의되며, 순간적인 일반 치르피티 c는 정상화된 버전이다.

${\displaystyle \pi(t)={\frac {d^{2}\pi(t)}{dt^{2}}:{\frac {d\omega(t)}{dt},\c(t)={\frac {d}{d}{dt}}}}}}}}}}$

따라서 처리는 순간 주파수의 변화율이다.^[2]

종류들

선형

	선형 처프(0:11) 선형 처림의 소리 예(5회 반복)
이 파일을 재생하는 데 문제가 있으십니까? 미디어 도움말을 참조하십시오.

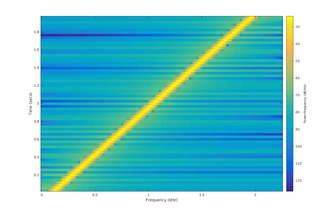
선형 주파수가 짹짹거리거나 단순히 선형적인 짹짹거리는 경우, 순간 주파수 $f{\displaystyle (t}$ ) ${\displaystyle f(t)}$은 시간에 따라 정확하게 선형적으로 변화한다$$.

${\displaystyle f}$( ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle c}$ ${\displaystyle t}$+ ${\displaystyle {f\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\$

여기서 $f{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) 시작 주파수(${\displaystyle \mathrm{시간}}$ t${\displaystyle }$=$$0 {\$displaystyle$ t$=0})$이고$$c {\$displaystyle c}$은(는) 처프 속도(chirp rate), 가정된 상수:

${\$$$$T$

여기서 $f{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}는$$ 최종 주파수이고, T$${\$displaystyle$ $t}은($는$)$ f ${\displaystyle {0\mathrm{}}_{}}$ ${\$ f_{0}}에서 ${\displaystyle {f\mathrm{}}_{}}$ 1$${\$displaystyle f_{1$}까지 스위프하는 데 걸리는$$ 시간이다$.$

The corresponding time-domain function for the phase of any oscillating signal is the integral of the frequency function, as one expects the phase to grow like ${\displaystyle \phi (t+\Delta t)\simeq \phi (t)+2\pi f(t)\,\Delta t}$, i.e., that the derivative of the phase is the angular frequency ${\displaystyle {}^{}}$${\displaystyle {\varphi }^{}}$(${\displaystyle t}$)${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \pi }$ ${\displaystyle f}$( ${\displaystyle t}$) ${\displaystyle \phi '(t)=2\pi \,f(t$ .

선형 처림의 경우 다음과 같은 결과를 얻는다.

${\displaystyle {\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi \int _{0}^{t}\left(c\tau +f_{0}\right)\,d\tau \\&=\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right),\end{aligned}}}$

여기서 $\varphi {\displaystyle {}_{}}$ ${\$는 초기 $단계{\displaystyle }$(시간$$ t =$$0 $displaystyle t=0$})$$이다$.$ 따라서 이것을 2상 신호라고도 한다.^[3]

사인파 선형 처프에 해당하는 시간 영역 함수는 라디안 단위로 위상의 사인이다.

${\displaystyle x(t)=\sin \left[\phi _{0}+2\pi \leftpi\frac {c}{2}}t^{2}+f_{0}t\right]}}}$

지수적

	지수 처프(0:05) 지수 짹짹거리는 소리 예제(5회 반복)
이 파일을 재생하는 데 문제가 있으십니까? 미디어 도움말을 참조하십시오.

기하급수적 짹짹이라고도 하는 기하학적 짹짹에서 신호의 주파수는 시간이 지남에 따라 기하학적 관계에 따라 변한다. In other words, if two points in the waveform are chosen, ${\displaystyle t_{1}}$ and ${\displaystyle t_{2}}$, and the time interval between them ${\displaystyle t_{2}-t_{1}}$ is kept constant, the frequency ratio ${\displaystyle f\left(t_{2}\right)/f\left$$(t_{1}\right)}$도 일정하게 된다$$.

지수 짹짹거리는 경우 신호의 주파수는 시간 함수에 따라 기하급수적으로 변한다.

${\displaystyle f(t)=f_{0}k^{t}}}$

여기서 $f{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) $시작{\displaystyle }$ 주파수${\displaystyle (\mathrm{t}}$= 0 {\$displaystyle$ t$=0})$이고$$k {\$displaystyle k}$은(는) 주파수 지수 변화율이다. 끊임없는 짹짹거리는 선형적인 짹짹과는 달리, 지수적인 짹짹이는 기하급수적으로 증가하는 빈도수를 가진다.

${\displaystyle k=\left({\frac {f_{1}:{f_{0}}\right)^{\frac {1}{{1}{f_}}{{1}}}}{\frac}{1}{}}T}}$

지수 짹짹의 위상에 해당하는 시간 영역 함수는 주파수의 정수다.

${\displaystyle {\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi f_{0}\int _{0}^{t}k^{\tau }d\tau \\&=\phi _{0}+2\pi f_{0}\left({\frac {k^{t}-1}{\ln(k)}}\right)\end{aligned}}}$

여기서 $\varphi {\displaystyle {}_{}}$ ${\$는 초기 단계($t$ =$$ $displaystyle t=0$})이다$.$

사인파 지수 처프에 해당하는 시간 영역 함수는 위상의 사인(라디안):

${\displaystyle x(t)=\sin \left[\phi _{0}+2\pi f_{0}\frac {k^{t}-1}{\ln(k)}\right]}}}$

선형 치프의 경우와 마찬가지로 지수 치프의 순간 주파수는 추가 고조파를 동반한$$ 기본 주파수 $f{\displaystyle (}$ ${\displaystyle t}$)${\displaystyle }$= f ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle k^{}}$ t ${\$로 구성된다.^{[citation needed]}

쌍곡선

쌍곡선 처림은 레이더 어플리케이션에서 사용되는데, 도플러 효과에 의해 왜곡된 후 최대 일치 필터 반응을 보이기 때문이다.

쌍곡선 처프에서 신호의 주파수는 시간의 함수로서 하이퍼볼릭적으로 변화한다.

${\displaystyle f(t)={\frac {f_{0}f_{1}T}{{(f_{0}-f_{1}T}{{1}{1}{(f_{1})t+f_{1}{1]}}T}}$

쌍곡선 처프 단계에 해당하는 시간 영역 함수는 주파수의 정수다.

${\displaystyle {\f_}\fi(t)&=\pi _{0}+2\pi \int_{0}^{t}f(\tau )\,d\tau \&=\pi _{0}+2\pi {-f_{0}f_{1}T}{f_{1}-f_{0}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}}}{f_{1}}}{f_{1}}}}{f_{11)}}T}t\오른쪽)\end{aigned}}$

여기서 $\varphi {\displaystyle {}_{}}$ ${\$는 초기 단계($t$ =$$ $displaystyle t=0$})이다$.$

사인파 쌍곡선 처프에 해당하는 시간 영역 함수는 라디안 단위의 위상의 사인이다.

${\displaystyle x(t)=\sin \left[\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}}}{f_{1}}}{f_{1}}}}{f_{11)}}T}t\오른쪽)\오른쪽]}$

세대

처프 신호는 전압 제어 오실레이터(VCO)를 통해 아날로그 회로와 선형 또는 기하급수적으로 증가하는 제어 전압을 통해 생성될 수 있다. 디지털 신호 프로세서(DSP)와 디지털-아날로그 컨버터(DAC)에 의해 디지털 생성될 수도 있고, 직접 디지털 신디사이저(DDS)를 사용하며, 수적으로 제어되는 오실레이터의 스텝을 변경하여 생성될 수도 있다. 그것은 또한 YIG 오실레이터에 의해서도 생성될 수 있다.^{[clarification needed]}

임펄스 신호와의 관계

짹짹거리는 신호는 임펄스 신호와 동일한 스펙트럼 함량을 공유한다. 그러나 임펄스 신호와 달리, 처프 신호의 스펙트럼 구성 요소는 상이 다르다.^[4][5][6] 즉, 파워 스펙트럼은 유사하지만 위상 스펙트럼은 구별된다. 신호 전파 매체의 분산은 의도하지 않게 충격 신호가 처림으로 변환되는 결과를 초래할 수 있다. 반면, 처림 펄스 증폭기나 초음파 위치 측정 시스템과 같은 많은 실제 애플리케이션은 본질적으로 낮은 피크 대 평균 전력 비율(PAPR) 때문에 충동 대신 처림 신호를 사용한다.^[6]

사용 및 발생

처프 변조

디지털 통신을 위한 선형 주파수 변조인 치프 변조(Chirp modulation)는 1954년 시드니 달링턴에 의해 특허를 받았으며, 이후 윙클러가 1962년에 수행한 상당한 양의 작업이 있었다. 이 유형의 변조는 순간 주파수가 시간에 따라 선형적으로 증가하거나 감소하는 사인파 파형을 사용한다. 이러한 파형을 흔히 선형 짹짹거리거나 단순히 짹짹거리는 소리라고 한다.

따라서 그들의 빈도가 변하는 속도를 짹짹거리는 속도라고 부른다. 이항 처프 변조에서, 이항 데이터는 비트를 반대 처프 속도의 처림으로 매핑하여 전송된다. 예를 들어, 1비트 기간 동안 "1"은 양의 비율 a로, "0"은 음의 비율 -a로 짹짹거리는 것이 할당된다. 짹짹은 레이더 애플리케이션에서 많이 사용되어 왔으며 그 결과 전송을 위한 고급 소스 및 선형 짹짹의 수신을 위한 일치 필터를 사용할 수 있다.

처플릿 변환

또 다른 종류의 지저귐은 투영적인 짹짹이다.

${\displaystyle g}$= ${\displaystyle f}$ ${\displaystyle \frac{\cdot }{}}$ ${\displaystyle \frac{x}{}}$ +${\displaystyle \frac{b}{}}$ ${\displaystyle \frac{}{}}$ ${\displaystyle \frac{\cdot }{}}$ ${\displaystyle \frac{\mathrm{x}}{}}$ ${\$}:{c\cdot x+1$}\right$

세 매개변수 a(척도), b(척도), c(척도)를 갖는 것. 투사적 처림은 영상 처리에 이상적으로 적합하며 투사적 처림 변환의 기초를 형성한다.^[2]

열쇠가 짹짹 울다.

RF 오실레이터의 안정성 저하로 원하는 주파수에서 Morse 코드의 주파수 변화를 chirp라고 하며,^[7] R-S-T 시스템에서는 문자 'C'가 추가된다.

참고 항목

위키미디어 커먼즈에는 치프와 관련된 미디어가 있다.

• 처프 스펙트럼 - 처프 신호의 주파수 스펙트럼 분석
• Chirp 압축 - 압축 기술에 대한 추가 정보
• IMT-2000 3GPP - 무선 통신 표준 IEEE 802.15.4a CSS의 일부
• 삐걱삐걱거울
• 삐걱거리는 펄스 증폭
• Chirplet 변환 - 지역화된 chirp 함수의 제품군을 기반으로 한 신호 표현.
• 연속파 레이더
• 분산(광학)
• 펄스 압축
• 전파 전파

메모들

참조

외부 링크

무료 사전인 Wiktionary에서 짹짹거리는 소리를 찾아 보십시오.

• Online Chirp Tone Generator(웨이브 파일 출력)
• 피시파인더에서 CHRP 음파탐지기
• 피시파인더에서 CHRP 음파탐지기