복합 랜덤 변수

확률 이론과 통계에서, 복합 랜덤 변수는 실제 가치의 랜덤 변수를 복잡한 숫자에 일반화하는 것이다. 즉, 복합 랜덤 변수가 취할 수 있는 값은 복합적인 숫자일 수 있다.^[1]복잡한 랜덤 변수는 항상 실제 랜덤 변수의 쌍, 즉 실제 및 가상 변수의 쌍으로 간주될 수 있다.따라서 하나의 복잡한 랜덤 변수의 분포는 두 개의 실제 랜덤 변수의 공동 분포로 해석될 수 있다.

실제 랜덤 변수의 일부 개념은 복잡한 랜덤 변수(예: 복잡한 랜덤 변수의 평균 정의)에 대한 간단한 일반화를 가지고 있다.다른 개념들은 복잡한 무작위 변수에 독특하다.

복잡한 무작위 변수의 적용은 디지털 신호 처리,^[2] 2차 진폭 변조 및 정보 이론에서 찾을 수 있다.

통계에 대한 시리즈 일부
확률론
확률 공리 결정론 시스템 인디테르민주의 무작위성
확률공간 샘플 공간 이벤트 총체적으로 철저한 사건들 초등 이벤트 상호배타성 결과 싱글턴 실험 베르누이 재판 확률분포 베르누이 분포 이항 분포 정규 분포 확률측도 변량변수 베르누이 과정 연속 또는 이산형 기대값 마르코프 체인 관측치 무작위 보행 확률적 과정
보완적 사건 관절확률 한계 확률 조건부 확률
독립 조건부 독립성 전체 확률의 법칙 대수의 법칙 베이즈 정리 부울의 부등식
벤 다이어그램 트리 다이어그램
v t

정의

A complex random variable ${\displaystyle Z}$ on the probability space ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ is a function ${\displaystyle Z\colon \Omega \rightarrow \mathbb {C} }$ such that both its real part ${\displaystyle \Re {(Z)}}$ and its imaginary part ${\displaystyle \mathrm{\Im }(Z)}$${\displaystyle \Im(Z)}$은$({\displaystyle \mathrm{\Omega },}$ ${\displaystyle F,}$ ${\displaystyle P)}$ ${\displaystyle(\Oomega,{\mathcal{F},P)}$ 의 실제 랜덤 변수 입니다$.$

예

간단한 예

표에 지정된 확률로 세$$ $가지{\displaystyle \mathrm{}}$ 복합 값 1,${\displaystyle i,2}$ ${\displaystyle 1+i, 1-i,$2}만 사용할 수 있는 랜덤 변수를 고려하십시오.이것은 복잡한 랜덤 변수의 간단한 예다.

확률 $P{\displaystyle }$( ${\displaystyle z}$) ${\디스플레이$ 스타일 $P(z)}$	$값{\displaystyle }$ z ${\displaystyle z}$
${\displaystyle {\frac {1}{4}}$	$(\displaystyle 1+i}$
${\displaystyle {\frac {1}{4}}$	$1-i}$
${\displaystyle {\frac {1}{2}}:}$	${\displaystyle 2}$

이 랜덤 변수의 기대치는 다음과 같이 간단하게 계산할 수 있다.${\displaystyle \operatorname {E} [Z]={\frac {1}{4}}(1+i)+{\frac {1}{4}}(1-i)+{\frac {1}{2}}2={\frac {3}{2}}.$$}$

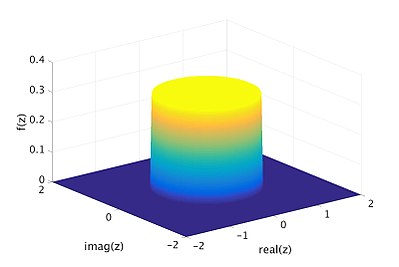
균등분포

복합 랜덤 변수의 또 다른 예로는 채워진 단위 원을 통한 균일한 분포가 있다. 즉, ${\displaystyle \mathrm{세트}}{\displaystyle }${ z ${\displaystyle \in }$ ${\displaystyle C\mathbb{}}$ ${\displaystyle \mid }$ ${\displaystyle z}$ ${\displaystyle \le }$ ${\displaystyle 1}$} ${\displaystyle \{z\in \mathb {C} \mid$ z $\leq 1$이 랜덤 변수는 확률밀도함수가 정의된 복합 랜덤 변수의 예다.밀도 함수는 다음 그림에서 황색 원반과 진한 청색 원반으로 표시된다.

복합정규 분포

복잡한 가우스 랜덤 변수는 종종 애플리케이션에서 발견된다.그것들은 실제 가우스 랜덤 변수의 간단한 일반화다.다음 그림은 그러한 변수의 분포의 예를 보여준다.

누적분포함수

$P{\displaystyle (Z}$ ${\displaystyle \le }$ ${\displaystyle 1}$+ ${\displaystyle 3}$ i$){\displaystyle P(Z\leq 1+3i)}$ 형식의 표현은 말이 되지$$ 않기 때문에 실제 랜덤 변수에 대한 누적 분포 함수의 일반화는 명확하지 않다.$그러나{\displaystyle }$ P${\displaystyle (}$ ${\displaystyle \mathrm{\Re }}$ ${\displaystyle (Z}$) ${\displaystyle \le }$ ${\displaystyle 1}$, ${\displaystyle ,}$(${\displaystyle Z}$) ${\displaystyle 3}$3 )$\displaystyle P(\Re$ (Z$)}\leq 1,\Im {(Z)}\leq$ 3) $형식$의 표현은 타당하다$$.따라서 우리는 실제 및 가상 부품의 공동 분포를 통해 복합 랜덤 변수의 누적$$ ${\displaystyle {분포}_{}}$ F Z${\displaystyle }$→${\displaystyle }$[ ${\displaystyle 0}$, ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle F_{Z}\mathb {C} \to [0,1]}$을(를) 정의한다.

확률밀도함수

The probability density function of a complex random variable is defined as ${\displaystyle f_{Z}(z)=f_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})}$, i.e. the value of the density function at a point ${\displaystyle z\in \mathbb {C} }$ is defined to be equal to점$({\displaystyle }$ ${\displaystyle \mathrm{\Re }}$( ${\displaystyle z}$)${\displaystyle }$, ${\displaystyle \mathrm{\Im }}$( z )${\displaystyle }$, ${\displaystyle \Im }$ ( )${\displaystyle (\Re {(z)},\Im {(z)})$에서 평가된 랜덤 변수의 실제 부분과 가상 부분의 조인트 밀도 값$.$

An equivalent definition is given by ${\displaystyle f_{Z}(z)={\frac {\partial ^{2}}{\partial x\partial y}}P(\Re {(Z)}\leq x,\Im {(Z)}\leq y)}$ where ${\displaystyle x=\Re {(z)}}$ and ${\displaystyle y=\Im {(z)}}$.

실제 경우와 마찬가지로 밀도 함수는 존재하지 않을 수 있다.

기대

복합 랜덤 변수에 대한 기대는 실제 랜덤 변수에 대한 기대의 정의에 기초하여 정의된다.^{[3]: p. 112}

$E{\displaystyle \mathrm{}}$ ${\displaystyle }$[ ${\displaystyle \Re }$( Z${\displaystyle }$) ${\displaystyle ]}$ ${\displaystyle \operatorname {E}[\Re {($${\displaystyle Z}$$)}]$ 또는$$ $E{\displaystyle \mathrm{}}$ ${\displaystyle }$[ ${\displaystyle \mathrm{\Im }}$( Z${\displaystyle }$) ${\displaystyle ]}$ ${\displaysty \operatorname {E}[\Im (Z)}]$이(가) 존재하지$$ 않는 경우 복합 랜덤 변수의 기대는 존재하지 않는다는 점에 유의하십시오.

If the complex random variable ${\displaystyle Z}$ has a probability density function ${\displaystyle f_{Z}(z)}$, then the expectation is given by ${\displaystyle \operatorname {E} [Z]=\int _{\mathbb {C} }z\cdot f_{Z}(z)dz}$.

If the complex random variable ${\displaystyle Z}$ has a probability mass function ${\displaystyle p_{Z}(z)}$, then the expectation is given by ${\displaystyle \operatorname {E} [Z]=\sum _{z\in \mathbb {Z} }z\cdot p_{Z}(z)}$.

특성.

복잡한 무작위 변수에 대한 기대가 존재할 때마다 기대와 복잡한 결합 통근:

${\displaystyle {\overline {\operatorname {E} [Z]}=\operatorname {E} [{\overline {Z}]}$

기대값 연산자 E ${\displaystyle }$[ ${\displaystyle \cdot }$ ${\displaystyle ]}$ ${\displaystyle \operatorname {E}[\cdot ]}$은(는) 다음과 같은 의미에서 선형이다.

${\displaystyle \operatorname {E} [aZ+bW]=a\operatorname {E} [Z]+b\operatorname {E} [W]}$

$모든{\displaystyle }$ 복잡한 $계수$의 ${\displaystyle \mathrm{경우}}$,$$Z {\$displaystyle Z}$과 $W{\displaystyle }$ ${\displaystyle W}$이(가) 독립적이지 않더라도$$, a${\displaystyle }$, b ${\displaystyle$ a$,b}$

분산 및 유사분산

분산은 절대 제곱의 관점에서 다음과 같이 정의된다.^{[3]: p. 117}

특성.

분산이 항상 음수가 아닌 실수다.이 값은 복합 랜덤 변수의 실제 부분과 가상 부분의 분산을 합한 값과 같다.

${\displaystyle \operatorname {Var} [Z]=\operatorname {Var}[\Re {(Z)}]+\operatorname {Var}[\Im {(Z)}]].}$

복합 랜덤 변수의 선형 조합의 분산은 다음 공식을 사용하여 계산할 수 있다.

${\displaystyle \operatorname {Var} \left[\sum _{k=1}^{N}a_{k}Z_{k}\right]=\sum _{i=1}^{N}\sum _{j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].}$

의사분산

의사분산은 의사 공분산의 특별한 경우로서, 일반 복합 제곱의 관점에서 정의되며, 다음과 같이 주어진다.

항상 현실적이고 양적인$$$Z{\displaystyle }$ ${\displaystyle Z}$의 분산과 달리, $Z{\displaystyle }$ ${\displaystyle Z}$의 유사분산은 일반적인 복합체다$$.

실제 부품과 가상 부품의 공분산 행렬

일반 복합 랜덤 변수의 경우 쌍(${\displaystyle }$( (${\displaystyle Z}$ )${\displaystyle }$,${\displaystyle }$, (${\displaystyle Z}$) )${\displaystyle (\$Re ${(Z)},\Im {(Z)})$에는 다음과 같은 형식의 공분산 행렬이 있다$$.

${\displaystyle {\begin{bmatrix}\operatorname {Var} [\Re {(Z)}]&\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]\\\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]&\operatorname {Var} [\Im {(Z)}]\end{bmatrix}}}$

The matrix is symmetric, so ${\displaystyle \operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]}$

그 요소들은 동일하다:

${\displaystyle{\begin{정렬}&,\operatorname{바르}[\Re{(Z)}]={\tfrac{1}{2}}\operatorname{리}(\operatorname{K}_{ZZ}+\operatorname{J}_{ZZ})\\&,\operatorname{바르}[\Im{(Z)}]={\tfrac{1}{2}}\operatorname{리}(\operatorname{K}_{ZZ}-\operatorname{J}_{ZZ})\\&,\operatorname{Cov}[\Re{(Z)},\Im{(Z)}]={\tfrac{1}{2}}\operatorname.{나는}(\oper아토르나메 {J} _{ZZ}\\\end{arged}}}$

반대로:

${\displaystyle {\begin{aligned}&\operatorname {K} _{ZZ}=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}]\\&\operatorname {J} _{ZZ}=\operatorname {Var} [\Re {(Z)}]-\operatorname {Var} [\Im {(Z)}]+i2\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]\end{aligned}}}$

공분산 및 의사 공분산

${\displaystyle 두}$ 복합 랜덤 변수 $Z{\displaystyle }$, W ${\displaystyle$ Z$,$$W}$이(가) 다음과^{[3]: p. 119} 같이 정의됨

정의에서 두 번째 인자의 복잡한 결합에 주목한다.

실제 랜덤 변수와 대조적으로 유사 공분산(보완적 분산이라고도 함)도 정의한다.

두 번째 순서 통계는 공분산과 의사 공분산이 완전히 특징이다.

특성.

공분산에는 다음과 같은 속성이 있다.

• ${\displaystyle \mathrm{Cov}}$ ${\displaystyle }$[ ${\displaystyle Z}$, ${\displaystyle W}$ ${\displaystyle ]}$= ${\displaystyle \stackrel{}{\mathrm{Cov}}}$ ${\displaystyle \stackrel{}{}}$[ ${\displaystyle \stackrel{}{W}}$, ${\displaystyle \stackrel{}{Z}}$ ${\displaystyle \stackrel{}{]}}$의${\$콘주게이트 대칭)
• ${\displaystyle \mathrm{Cov}}$ ${\displaystyle }$[${\displaystyle \alpha }$ Z${\displaystyle }$, ${\displaystyle W}$ ${\displaystyle ]}$= ${\displaystyle \alpha }$ ${\displaystyle \mathrm{Cov}}$ ${\displaystyle }$[ Z${\displaystyle }$, ${\displaystyle W}$ ${\displaystyle ]}$ ${\displaystyle \operatorname {Cov}[\alpha Z,W]=\alpha \operatorname {Cov}[Z,W]}($세쿼리성)
• ${\displaystyle \operatorname {Cov} [Z,\alpha W]={\overline {\alpha }\operatorname {Cov} [Z,W]}}$
• ${\displaystyle \operatorname {Cov} [Z_{1}+Z_{2},W]=\operatorname {Cov} [Z_{1},W]+\operatorname {Cov} [Z_{2},W]}$
• ${\displaystyle \operatorname {Cov} [Z,W_{1}+{2}]=\operatorname {Cov} [Z,W_{1}]+\operatorname {Cov} [Z,W_{2}]}$
• ${\displaystyle \operatorname {Cov} [Z,Z]={\operatorname {Var}[Z]}}}$
• 비관련성: $K{\displaystyle {\mathrm{}}_{}}$ ${\displaystyle Z_{}}$ ${\displaystyle W_{}}$= ${\displaystyle \mathrm{J}}$ ${\displaystyle Z_{}}$ W${\displaystyle {}_{}}$= 0 ${\displaystyle \operatorname {K} _{ZW}=\operatorname {J} _{Z$} _{Z} 복잡한 임의 $변수{\displaystyle }$ Z ${\$displaystystyle W$}$와 W ${\displaystystysty$ W$}$이 비관련성이 호출된다.$W}=0}($참조: 상관 없음(확률 이론) 참조).
• 직교성: $E{\displaystyle \mathrm{}}$ ${\displaystyle }$[${\displaystyle \mathrm{Z}}$ ${\displaystyle W\stackrel{}{}]}$= 0 ${\displaystyle \operatorname {E}[Z{\overline {W}]=0$인 경우 두 개의 복합 랜덤 변수 $Z{\displaystyle }$ ${\displaystyle$Z} $및$ W$${\$displaystysty W}$을 직교라고 한다.

원형대칭

복잡한 랜덤 변수의 원형 대칭은 무선 통신 분야에서 사용되는 일반적인 가정이다.원형 대칭 복합 랜덤 변수의 대표적인 예로 평균이 0이고 의사 공분산 행렬이 0인 복잡한 가우스 랜덤 변수가 있다.

$복합{\displaystyle }$ 랜덤 변수 Z ${\$${\displaystyle \mathrm{displaystyle}}$ $Z}$이$($가) 모든 $결정론적{\displaystyle [[}$ - ${\displaystyle ,}$ , ] ${\displaystyle ]}$에 $대해{\displaystyle {}^{}}$$$e ${\displaystyle {}^{}}$ Z ${-\pi ,\pi \pi$$$\}}의 분포가 Z$$${\displaystyle e^{\mathrmatm {i} \$$phi}$의 분포와 같으면$$ 원형 대칭이다$.$

특성.

정의에 따르면, 원형 대칭 복합 랜덤 변수는

모든 $\varphi {\displaystyle }$ ${\displaystyle \phi }$에 대해$.$

따라서 원형 대칭 복합 랜덤 변수의 기대치는 0이거나 정의되지 않을 수 있다.

또한.

모든 $\varphi {\displaystyle }$ ${\displaystyle \phi }$에 대해$.$

따라서 원형 대칭 복합 랜덤 변수의 유사-분산은 0일 수 있다.

$Z{\displaystyle }$ ${\displaystyle Z}$과 $e{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ Z ${\displaystyle$ e$^{\mathrm {i} \pi$ ${\displaystyle \}}$$Z}$이(가) 동일한 분포를 갖는$$ 경우$,$ Z {\$displaystyle$ $Z}$의 위상은${\displaystyle }$[ -${\displaystyle \pi }$ ,$\$] ${\pi ,\$pi ]에 걸쳐 균일하게 분포되어야 하며$$$$$,$ $Z{\displaystyle }$ {\dispi}의 진폭에 독립되어야 한다$.$^[4]

적절한 복합 랜덤 변수

적절한 랜덤 변수의 개념은 복잡한 랜덤 변수에 고유하며 실제 랜덤 변수를 가진 통신원 개념이 없다.

다음과 같은 세 가지 조건이 모두 충족되면 복합 랜덤 $변수{\displaystyle }$ Z ${\displaystyle$ Z$}$을(를) 적절한 것으로 부른다$$.

• ${\displaystyle \operatorname {E} [Z]=0}$
• ${\displaystyle \operatorname {Var} [Z]<\fty }$
• ${\displaystyle \operatorname {E} [Z^{2}]=0}$

이 정의는 다음과 같은 조건에 해당한다.즉, 다음과 같은 경우에만 복합 랜덤 변수가 적절하다는 것을 의미한다.

• ${\displaystyle \operatorname {E} [Z]=0}$
• ${\displaystyle \operatorname {E}[\Re {(Z)}^{2}]=\operatorname {E}[\Im {(Z)}^{2}]\neq \infty }}}$
• ${\displaystyle \operatorname {E}[\Re {(Z)}\Im {(Z)}]=0}$

적절한 복합 랜덤 변수의 경우, 쌍$({\displaystyle }$ ${\displaystyle \mathrm{\Re }}$( ${\displaystyle Z}$)${\displaystyle }$, ${\displaystyle \mathrm{\Im }}$( ${\displaystyle Z}$)${\displaystyle (\Re {(Z)},\Im {(Z)})$의 공분산 행렬은 다음과 같은 간단한 형태를 가진다$$.

[ [ Z ${\$ {$1}{1}{1}{bmatrix$

예:

${\displaystyle {\begin{aligned}&\operatorname {Var} [\Re {(Z)}]=\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Var} [Z]\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=0\\\end{aligned}}}$

카우치-슈바르츠 불평등

삼각형 불평등과 쾰더의 불평등을 이용하여 도출할 수 있는 복잡한 랜덤 변수에 대한 코치-슈워즈 불평등은 다음과 같다.

${\displaystyle \left \operatorname {E} \left[Z{\overline {W}}\right]\right ^{2}\leq \left \operatorname {E} \left[\left Z{\overline {W}}\right \right]\right ^{2}\leq \operatorname {E} \left[ Z ^{2}\right]\o$$peratorname {E} \left[W ^{2}\right]}$.

특성함수

복합 랜덤 변수의 특성 함수는 다음과${\displaystyle }같이{\displaystyle \mathbb{}}$ ${\displaystyle 정의}$된 함수$$C → C {\$displaystyle \mathb {C} \to$\mathb$$ {$C}$이다.

${\displaystyle \varphi _{Z}(\omega )=\operatorname {E} \left[e^{i\Re({\overline {\omega }Z)}}\오른쪽]=\operatorname {E} \left[e^{i(\re {(\omega )}\Re {(Z)}+\Re {(Z)}Im(\omega)}\Im {(Z)}}\right].}$

참고 항목

• 중앙 모멘트
• 복합 랜덤 벡터

참조