큐빅과 16-셀의 화합물

테세락트 16셀 화합물
유형	화합물
슐레플리 기호	{4,3,3} ∪ {3,3,4}
콕시터 다이어그램	∪
교차로	가늘게 말린 큐브락트
볼록 선체	24셀
폴리초라	2: 1 테서락트 16 셀 1
폴리헤드라	24: 8입방체 사면체 16
얼굴	56: 24제곱 삼각형 32개
가장자리	56
정점	24
대칭군	초옥타헤드 대칭 [4,3,3] 주문 384

4차원 기하학에서 큐빅 16세포 화합물은^[1] 일반 큐빅과 이중 정규 16세포로 구성된 폴리토프 화합물이다.복합 폴리토페는 공통의 중심을 공유하는 여러 개의 폴리토페로 구성된 형상이다.화합물의 바깥쪽 정점들은 볼록한 선체라고 불리는 볼록한 폴리토프를 형성하기 위해 연결될 수 있다.그 화합물은 볼록한 선체를 방조하는 것이다.

이중 쌍으로 구성된 4-폴리토프 화합물에서, 셀과 정점은 면과 가장자리의 위치를 교환한다.이 때문에 면과 가장자리와 마찬가지로 셀과 정점의 수가 같다.큐빅의 중간 에지는 16 셀에서 중간 면과 교차하며, 그 반대의 경우도 마찬가지다.

큐브와 팔면체의 화합물의 4차원 아날로그라고 볼 수 있다.

이것은 일반 볼록 4폴리토프와 그것의 이중성을 결합하여 얻은 네 개의 복합 폴리토페 중 하나이다. 다른 세 개는 두 개의 24셀의 화합물이고 120셀과 600셀의 화합물인 두 개의 5셀의 화합물이다.

건설

화합물의 꼭지점에 대한 24개의 데카르트 좌표는 다음과 같다.

8: (±2, 0, 0, 0), ( 0, ±2, 0, 0), ( 0, 0, ±2, 0), ( 0, 0, 0, ±2)

16: ( ±1, ±1, ±1, ±1)

이것들은 16세포의 처음 두 개의 꼭지점 집합이다.^[2]

파켓팅

볼록한 선체는 자가이중 정규 24세포로, 이 역시 정류된 16세포다.이로써 24셀의 면모를 갖추게 되었다.

큐브와 16-셀 화합물의 교차점은 균일한 박리 큐트 큐브 큐브 큐브 큐브 큐브 입니다.

B4 Coxeter 평면의 그래프

요소들		화합물	볼록 선체	교차로
테세락트	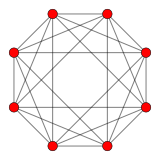16 셀	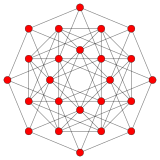테세락트 16세포	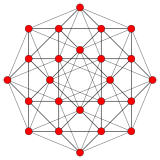셀프 듀얼 24셀	비트런티드 테세락트
		∪	= =

참고 항목

• 5-큐브와 5-정맥의 합성어

참조

• Weisstein, Eric W. "Tesseract". MathWorld.
• Weisstein, Eric W. "16-Cell". MathWorld.

외부 링크

• 테세락트와 그것의 이중, 16-셀의 화합물
• 큐브와 이중의 회전 화합물