5세포

일반 5-셀
(펜타코론)
(4-980x)
일반 5-셀; (펜타코론); (4-980x)
	슐레겔 도표; (수직 및 가장자리)
유형	볼록 정규 4폴리토프
슐레플리 기호	{3,3,3}
콕시터 다이어그램
세포	5 {3,3}
얼굴	10 {3}
가장자리	10
정점	5
정점수	; (삼면체)
페트리 폴리곤	오각형의
콕시터군	A4, [3,3,3]
이중	셀프듀얼
특성.	볼록, 이등변, 동위원소, 등면체
균일지수	1

단순 회전을 수행하는 5-셀의 3D 투영

그물 5개(숨겨진 1개)

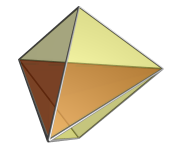
기하학에서 5세포는 슐레플리 기호 {3,3,3}이(가) 있는 볼록 4폴리토프다.그것은 5개의 4차원 물체로서 5개의 4차원 세포로 경계를 이루고 있다.^[a]C₅, 펜타코론,^[1] 펜타코프, 펜타코프,^[2] 펜타헤드로이드 또는 사면피라미드로도 알려져 있다.그것은 4-심플렉스( $\alpha _{4}$ 의 $\alpha _{4}$ 4 {\ $displaystyle \alpha_{4$ }폴리토페 $\alpha _{4}$ )^[3]로, 가능한 가장 단순한 볼록 4-폴리토프로서, 3차원에서는 사면체, 2차원에서는 삼각형과 유사하다.5세포는 4차원 피라미드로 4면 기단과 4면이다.

정규 5전지는 5개의 정규 4전지로 경계를 이루며, 6개의 정규 볼록 4폴리토프(플라토닉 고형물의 4차원 유사점) 중 하나이다.정규 5셀은 4면체의 모든 정점으로부터 한 가장자리 길이의 5번째 정점을 추가함으로써 정규 4면체로부터 구성될 수 있다.이것은 3차원 공간에서는 할 수 없다.정규 5셀은 이 문제에 대한 해결책이다.모든 삼각형의 각 면이 정확히 하나의 성냥개비인 10개의 성냥개비를 사용하여 모두 같은 크기의 정삼각형 10개를 만든다.3차원으로 해결책은 존재하지 않는다.

대체 이름

펜타초론(5점 4폴리토프)
비대면(사면체의 4차원 아날로그)
4차원 심플렉스(4차원 심플렉스)
사면피라미드(사면피라미드 4차원, 사면피라미드
펜타토페
펜타헤드로이드(헨리 파커 매닝)
펜(Jonathan Bowers: 펜타코론용)^[4]

기하학

5-셀은 4차원 심플렉스, 가능한 4-폴리토프 중에서 가장 단순하다.이와 같이 6개의 볼록 정규 4폴리탑(크기 및 복잡도 순서)의 순서에서 첫 번째다.^[b]

정규 볼록 4폴리톱
대칭군	A을₄	B₄		F₄	H₄
이름	5세포 초계면체 5점	16 셀 초옥타헤드론 8점	8셀 하이퍼큐브 16점	24셀 24점	600셀 고이코사면체 120점	120 셀 초도면체 600점
슐레플리 기호	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
콕시터 미러
그래프
정점	5	8	16	24	120	600
가장자리	10	24	32	96	720	1200
얼굴	삼각형 10개	삼각형 32개	24제곱	96개의 삼각형	1200 삼각형	펜타곤 720개
세포	5 사면체	사면체 16	8입방체	24옥타헤드라	사면체 600개	도데카헤드라로120번길
토리	5축면체 1개	2 8수면체	2 4시 30분	4 6옥타이드론	30수면체 20	10도면체 12개
새겨진	120 셀에 120	16 셀 1	16-182로 2	3 8시 30분	5 24 x 5	600 x 2의 5 x 2
그레이트 폴리곤		2 𝝅/2squares x 3	직사각형 4개/2개 x 3개	4㎛/3헥사곤 x 4	12㎛/5데카곤 x 6	50 //15 도데카곤 x 4
페트리 폴리곤	1오각형	팔각형 1개	옥타곤 2개	도데카곤 2개	30-gon 4개	30-gon 20
이소크라인 폴리곤		1 {8/2}=2{4} x {8/2}=2{4}	2 {8/2}=2{4} x {8/2}=2{4}	2 {12/2}=2{6} x {12/6}=6{2}	4 {30/2}=2{15} x 30{0}	20 {30/2}=2{15} x 30{0}
긴 반지름	1	1	1	1	1	1
모서리 길이	√5/√2 ≈ 1.581	√2 ≈ 1.414	1	1	1/ϕ ≈ 0.618	1/√2ϕ² ≈ 0.270
단반경	1/4	1/2	1/2	√2/2 ≈ 0.707	1 - (√2/2√3φ)² ≈ 0.936	1 - (1/2√3φ)² ≈ 0.968
면적	10•√8/3 ≈ 9.428	32•√3/4 ≈ 13.856	24	96•√3/4 ≈ 41.569	1200•√3/8φ² ≈ 99.238	720•25+10√5/8φ⁴ ≈ 621.9
볼륨	5•5√5/24 ≈ 2.329	16•1/3 ≈ 5.333	8	24•√2/3 ≈ 11.314	600•1/3√8φ³ ≈ 16.693	120•2 + φ/2√8φ³ ≈ 18.118
4-내용	√5/24•(√5/2)⁴ ≈ 0.146	2/3 ≈ 0.667	1	2	쇼트∙볼/4 ≈ 3.907	쇼트∙볼/4 ≈ 4.385

5-셀은 모두 같은 하이퍼플레인 안에 있지 않은 5개의 점으로 형성된다(사면체는 모두 같은 평면에 있지 않은 4개의 점으로 형성되며, 삼각형은 모두 같은 선에 있지 않은 3개의 점으로 형성된다).따라서 임의로 선택한 4-폴리토프 정점 5개는 보통 5-셀은 아니지만 5-셀을 구성한다.정규 5 셀은 다른 정규 볼록 4 폴리탑에서 찾을 수 없으며, 단 한 개를 제외하고 600-Vertex 120 셀은 120개의 정규 5 셀의 혼합물이다.^[c]

구조

4차원 공간에서 5개의 4면체 그물을 접어서 각 4면체가 다른 4면에 접합되면 결과 5면체는 5정점, 10 가장자리, 10면이다.네 개의 가장자리는 각 꼭지점에서 만나고, 세 개의 사면세포는 각 가장자리에서 만난다.

5세포는 (모든 심플렉스처럼) 자가이중이며, 정점자형은 사면체(Thetraheadron)이다.3차원 공간과의 최대 교차점은 삼각 프리즘이다.이음각은 cos⁻¹(1/4) 또는 약 75.52°이다.

이중 구성에서 두 개의 5-셀의 볼록한 선체는 분산형 30-셀이며, 이중은 5-셀이다.

구성으로

이 구성 매트릭스는 5-셀을 나타낸다.행과 열은 꼭지점, 가장자리, 면 및 셀에 해당한다.대각선 숫자는 5-셀 전체에서 각 원소가 얼마나 많이 발생하는지 말해준다.비대각 숫자는 열의 요소 중 몇 개가 행의 요소 안에서 또는 열 요소에서 발생하는지 알려준다.이 자기 이중 폴리토프의 매트릭스는 180도 회전과 동일하다.^[7]

${\displaysty}{bmatrix}{\\n4&6&4\\\2&10&3&3\\3&10&2\4&4&5\end{bmatrix}}}}$

좌표

가장 간단한 좌표 집합은 다음과 같다: (20,0,0,0,0), (0,0,0), (0,0,0,0,2), (0,0,0,0,2), (10,0,0,0,0,2), (195,6), 가장자리 길이 2/2이며, 여기서 golden은 황금 비율이다.^[8]

가장자리 길이 2와 반지름 1.6을 갖는 원점 중심의 일반 5-셀 정점의 데카르트 좌표는 다음과 같다.

\left\frac {1}{\sqrt {10}},\\frac {1}{\sqrt{6}},\\pm 1\오른쪽)

\left\frac {1}{\sqrt {10}},\\frac {1}{\sqrt {6},\\\frac {-2}{\sqrt {3},\ 오른쪽)

\left\frac {1}{{\sqrt {10}},\{\sqrt {3}{3}}}}\0,\ 0\ 오른쪽)

\left2{\sqrt {\frac {2}{5}},\ 0,\ 0\오른쪽)

4-공간에서 또 다른 원점 중심 좌표 세트는 3-공간에서 정규 사면기반을 갖는 초피라미드로 볼 수 있으며, 가장자리 길이는 2제2제2제2제2제2제2제2제2제2제2제2제2제2제2제2제3.2제3제2제3제2항의 반지름은 다음과 같다.

\left(1,1,1,{\frac {-1}{\sqrt{5}}\오른쪽)

\left(1,-1,-1,{\frac {-1}{\sqrt{5}}\오른쪽)

\left1,1,-1,{\frac {-1}{\sqrt{5}}\오른쪽)

\left1,-1,{\frac {-1}{\sqrt{5}}\오른쪽)

\left(0,0,0,{\frac {4}{\sqrt{5}}\오른쪽)

4-심플렉스(가장자리 √2 및 반지름 1)의 정점은 (간결함) 순열 (0,0,0,0,0,1) 또는 (0,1,1,1)의 경우 5-공간의 하이퍼플레인에서 보다 단순하게 구성될 수 있다. 이러한 위치에서는 각각 5-정렬 또는 정류된 penter의 한 면이다.

보어디크-콕시터나선

5개의 셀은 4차원 링으로 접혀진 5개의 사슬로 묶인 테트라헤드라의 보어디크-콕시터 나선형으로 구성될 수 있다.10개의 삼각형 면은 삼각형 타일링 내의 2D 그물에서 볼 수 있으며, 모든 꼭지점 주위에 6개의 삼각형이 있지만, 4-차원으로 접으면 가장자리가 일치한다.보라색 가장자리는 5-셀의 페트리 폴리곤을 나타낸다.

투영

A₄ Coxeter 평면은 5-cell을 일반 펜타그램과 펜타그램으로 투영한다.5-셀의₃ A Coxeter 평면 투영은 사각 피라미드의 평면 투영이다.일반 5-셀의 A₂ Coxeter 평면 투영은 두 정점이 중심인 삼각형 bipyramid(두 개의 테트라헤드라가 마주보고 결합됨)의 투영이다.

맞춤법 투사
A을_k 콕시터 평면	A을₄	A을₃	A을₂
그래프
치측 대칭	[5]	[4]	[3]

3차원 투영
5-셀을 3차원으로 정점 먼저 투영하는 것은 사면 투영 봉투가 있다.5세포의 가장 가까운 정점은 여기 빨간색으로 표시된 것처럼 사면체의 중심에 돌출되어 있다.가장 먼 세포는 사면체 봉투 자체에 투영되고, 다른 4개의 세포는 중앙 꼭지점을 둘러싼 4개의 평평한 사면체 영역에 투영된다.	5-셀을 3차원으로 가장 먼저 투영한 것은 삼각형 쌍극상 봉투를 가지고 있다.가장 가까운 가장자리(여기 빨간색으로 표시됨)는 dipyramid의 축에 투영되며, 이를 둘러싸고 있는 세 개의 세포는 이 축을 중심으로 배열된 3개의 사면체 볼륨에 투영된다.나머지 2개의 세포는 디피라미드의 두 반쪽으로 투영되어 펜타토프의 저쪽에 있다.
5셀을 3차원으로 얼굴 먼저 투영한 것에도 삼각형 쌍곡선 모양의 투영 봉투가 있다.여기서 가장 가까운 얼굴이 빨간색으로 표시되어 있다.이 얼굴에서 만나는 두 개의 세포는 쌍두엽의 두 반쪽으로 투영된다.나머지 3개의 셀은 4D 관점에서 펜타토프의 저쪽에 있으며 선명성을 위해 이미지에서 도태된다.그것들은 가장자리 첫 번째 투영에서와 마찬가지로 쌍극체의 중심 축을 중심으로 배열된다.	5셀을 3차원으로 먼저 투영하는 세포는 사면봉투를 가지고 있다.가장 가까운 셀은 전체 봉투에 투영되며, 4D 관점에서 나머지 4개의 셀은 여기에서 렌더링되지 않는다.

입체 투영 와이어프레임(3-sphere에 투사된 가장자리)

불규칙 5세포

5세포와 같은 심플렉스(simplex)의 경우 어떤 의미에서 특정한 불규칙적인 형태는 정규 형태보다 더 근본적이다.일반 5셀은 4공간이나 4폴리탑을 채울 수 없지만, 불규칙한 5셀이 있다.이러한 특징적인 5-셀은 다양한 4-폴리탑을 발생시키는 다른 대칭 그룹의 기본 영역이다.

정형외과

4정맥이란 10개의 면 모두가 직각 삼각형인 5세포다.^[a]직교란 모든 가장자리가 서로 수직인 나무의 볼록한 선체를 말한다.4차원 직교에서 트리는 세 개의 직각 회전을 하는 선형 경로에서 다섯 개의 정점을 모두 연결하는 네 개의 수직 가장자리로 구성된다.정형외과의 원소 또한 정형외과의 원소들이다. (일반 심플렉스 원소도 일반 심플렉스인 것처럼)4정맥의 각 사면세포는 3정맥이고, 각 삼각면은 2정맥(직삼각형)이다.

정형외과는 일반적인 폴리토페의 특징적인 단순함으로서, 각각의 규칙적인 폴리토페는 그것의 특정한 특징적인 정형외과의 경계면에서의 반사에 의해 생성되기 때문이다.^[9]예를 들어, 길이가 같은 수직 가장자리가 있는 4정맥의 특별한 경우는 3차원 큐브의 4차원 아날로그인 4-큐브(테서락트 또는 8-셀이라고도 함)의 특성 정형맥이다.4-정맥의 3개의 수직 가장자리가 단위 길이인 경우, 모든 가장자리의 길이는 √1, √2, √3, √4이며, 단위 4-큐브의 현 길이(4-큐브 가장자리와 그 다양한 대각선의 길이)이다.따라서 이 4정맥은 4-큐브 안에 들어맞고, 4-큐브(모든 일반 폴리토프처럼)는 그것의 특징적인 정맥의 예들로 해부될 수 있다.

3개의 관이 6개의 3개의 정문으로 해부되었다.셋은 왼손잡이고 셋은 오른손잡이다.네모난 얼굴마다 좌우의 만남.

3정식은 쉽게 묘사되지만 4정식은 시각화하기가 더 어렵다.4정형 피라미드는 3정형 피라미드를 베이스로 하는 4정형 피라미드다.3정맥보다 가장자리가 4개 더 많아, 베이스의 4정점(5-셀의 5정점)을 정점에 잇는다.3-큐브 일러스트에 표시된 6개 중 3-정형 중 하나를 고르십시오.큐브의 8개의 꼭지점 중 4개를 건드리며, 그 4개의 꼭지점은 직각으로 두 번 도는 3개의 에지 경로로 연결된다.이 3정맥이 4정맥의 기초가 된다고 상상해 보십시오. 그러면 그 4정맥에서 보이지 않는 4정맥 가장자리가 5번째 정점에 연결된다(3정맥 바깥에 있고 그림에 전혀 나타나지 않음).비록 네 개의 추가 가장자리가 모두 같은 꼭지점에 도달하지만, 그것들은 모두 길이가 다를 것이다.이들 중 첫 번째 것은 3-엣지 직교 경로의 한쪽 끝에서 3번째 90도 회전을 하고 정점에 수직으로 도달함으로써 4번째 직교 √1 에지로 그 경로를 확장한다.네 개의 추가 가장자리 중 두 번째는 입방체 면의 32 대각선이다(그림 3-큐브가 아니라 큐브 8개 중 다른 3-큐브).^[d]세 번째 추가 에지는 3-큐브(원래 그림 3-큐브가 아닌 3-큐브)의 diagonal3 대각선이다.네 번째 추가 에지(직교 경로의 다른 쪽 끝에서)는 길이 44의 테서락트 자체의 긴 직경이다.정점인 대척점(상대방 3관 정점)까지 정확한 큐빅의 중심을 통해 도달한다.따라서 4-큐브의 특징적인 심플렉스에는 4개의 √1 가장자리, 3개의 √2 가장자리, 2개의 √3 가장자리, 1개의 √4 가장자리가 있다.

4-큐브는 4개의 직교 4개의 직교 4개의 지름 각각을 둘러싸고 있는 6개의 직교 4개의 직교 4개의 직교 4개의 서로 다른 8개의 방법으로 해부될 수 있다.^[e]

보다 일반적으로 특징적인 심플렉스는 폴리토프의 모든 필수 요소(적절한 비율)를 가지고 있기 때문에 균일한 폴리토프를 채울 수 있다.^[f]직교체이기 때문에 원소 사이의 필수각(아래 90도)도 모두 가지고 있다.특징적인 심플렉스들은 폴리토페스의 유전암호다. 스위스 군용 칼과 같이, 복제에 의해 폴리토페어를 구성하는 데 필요한 모든 것 중 하나를 포함하고 있다.

일반 5-셀을 포함한 모든 일반 폴리토프는 그 특징적인 정형외과를 가지고 있다.일반 5세포의 특징적인 심플렉스인 4정기가 있다.일반 사면체의 특징적인 사면체(四面體)를 바탕으로 한 사면체 피라미드다.In a unit-radius 5-cell (edge length √2.5 ≈ 1.581) the 3-orthoscheme base has one longest √2.5 edge, two shortest √0.625 edges (half-edges of the regular 5-cell), two √1.875 edges, and one edge of length √5/2 = √1.118∼ (one of the three mid-edge to opposite mid-edge diameters of the regular tetrahedron).꼭지점에는 4개의 가장자리(각 길이 중 하나)가 추가되므로 4정맥에는 2개의 가장자리(일반 5-셀의 반대편과 수직방향 가장자리), 3개의 최단 00.625개의 가장자리(일반 5-셀의 반쪽 가장자리), 3개의 11.875개의 가장자리, 2개의 11.118~2의 가장자리(다른 4면체 직경)가 있다.4개의 직교 가장자리의 경로는 00.625, √1.118~, 00.625, √1.118~이다. (반쪽 가장자리의 경우, 사면 중심, 다른 반면 중심, 다른 사면 중심).일반 5세포는 일반적인 정규 5세포 가장자리를 둘러싸고 있는 6개의 4개의 4개의 다른 방법으로 10개의 4개의 직류체로 해부될 수 있다.^[g]

등각류

5-셀의 대칭 형태는 다음과 같이 균일한 폴리토프 정점 수치로 발견되는 것을 포함하여 많은 하위 대칭 형태가 있다.

대칭	[3,3,3] 주문로120번길	[3,3,1] 주문24	[3,2,1] 순서 12	[3,1,1] 순서 6	[5,2]⁺ 주문 10
이름	일반 5-셀	사면 피라미드	삼각피라미달 피라미드		오각형 하이퍼디스페노이드
슐레플리	{3,3,3}	{3,3} ∨ ( )	{3} ∨ { }	{3} ∨ ( ) ∨ ( )
예 꼭지점 형상을 나타내다	5와섹스	잘린 5-심플렉스	5-단순 비트런드	캔트런치 5-심플렉스	옴니트런드 4단백 벌집

사면피라미드는 다면피라미드인 5세포의 특수한 경우로, 3공간 하이퍼플레인에서 일반적인 사면피라미드 기지로 건설되고, 하이퍼플레인 위의 정점점으로 건설된다.피라미드의 4면은 4면체 세포로 이루어져 있다.

많은 균일한 5폴리탑은 사면 피라미드 꼭지점을 가지고 있다.

대칭 [3,3,1], 순서 24

이름 콕시터	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3}	t{4,3,3}	t{3,4,3,3}
슐레겔 도표를 만들다

다른 균일한 5-폴리탑은 5-셀 정점 수치가 불규칙하다.균일한 폴리토프의 정점 도형의 대칭은 Coxeter 다이어그램의 고리형 노드를 제거하여 나타낸다.

대칭	[3,2,1], 주문 12		[3,1,1], 주문 6		[2⁺,4,1], 주문 8	[2,1,1], 주문 4
슐레겔 도표를 만들다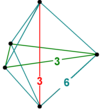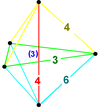
이름 콕시터	α₁₂₅	t₁₂₅	α₀₁₂₅	t₀₁₂₅	α₁₂₃₅	t₁₂₃₅

대칭	[2,1,1], 주문 2			[2⁺,1,1], 주문 2	[ ],⁺ 주문 1
슐레겔 도표를 만들다
이름 콕시터	α₀₁₂₃₅	t₀₁₂₃₅	t₀₁₂₃β₅	α₀₁₂₃₄₅	t₀₁₂₃₄₅

화합물

이중 구성에서 두 개의 5 셀의 화합물은 빨간색과 파란색 5 셀 정점과 가장자리를 가진 이 A5 Coxeter 평면 투영에서 볼 수 있다.이 화합물은 대칭이 [3,3,3]이며, 순서 240이다.이 두 개의 5-셀의 교차점은 균일한 비트코인 5-셀이다. = ∩ .

이 화합물은 2D 육각형 {6/2}의 4D 아날로그와 2개의 4차원 화합물로 볼 수 있다.

메모들

^ ^a ^b 5-셀의 5정점은 5개의 4면 세포를 서로 마주보고 있으며, 총 10개의 가장자리와 10개의 삼각면을 가지고 있다.
^ 볼록 정규 4폴리탑은 동일한 반지름에 대해 4차원 함량(초대량)의 척도로 크기별로 주문할 수 있다.순서에서 각각의 큰 폴리토프는 동일한 반경 내에 더 많은 내용을^[5] 포함하면서 이전보다 더 둥글다.4심플렉스(5셀)는 한계 최소 케이스, 120셀은 최대 케이스다.복잡성(구성 행렬 또는 정점 수를 비교하여 측정)은 동일한 순서를 따른다.이것은 5 셀이 5 포인트 4 폴리토프인 일반 폴리토페에 대한 대체 숫자 이름 지정 체계를 제공한다: 먼저 600 포인트 4 폴리토프로 이어지는 오름차순으로.
^ 일반 120 셀은 120개의 일반 도두면체 셀로 구성된 곡선 3차원 경계면을 가지고 있다.또한 120개의 분리형 일반 5셀이 새겨져 있다.^[6]이것들은 3차원 세포가 아니라 120세포의 중심점을 공유하는 4차원 물체로서, 그 정점 600개를 모두 포괄한다.
^ 4관(tesseract)에는 8개의 3관(tesseract)이 들어 있다(그래서 8세포라고도 한다).각각의 3-큐브는 다른 6개의 튜브에 면접 결합되지만(전적으로 그것을 둘러싸고 있는), 8-셀의 반대편에 놓여 있는 다른 3-큐브와는 완전히 분리된다.
^ 일반 폴리토프의 경우 생성 특성 정형외과메의 Coxeter-Dynkin 다이어그램은 생성 포인트 링이 없는 생성된 폴리토페의 다이어그램이다.
^ d 치수의 일반 폴리토프의 특성 심플렉스에는 d의 다른 길이의 가장자리가 있고 각 꼭지점에는 각 길이의 가장자리가 하나씩 있다.
^ 관련된 각도는 일반 심플렉스처럼 60도, 90도뿐이다.

인용구

^ N.W. Johnson: 지오메트리 및 변환, (2018) ISBN978-1-107-10340-5장: 유한대칭군, 11.5 구형 콕시터군, 페이지 249
^ 마틸라 기카, 예술과 삶의 기하학 (1977), 페이지 68
^ Coxeter 1973, 페이지 120, §7.2. 그림 7.2A를 참조하십시오.
^ 카테고리 1: 일반 폴리초라
^ Coxeter 1973, 페이지 292–293, 표 I(ii):4차원의 16개의 일반 폴리토페 {p,q,r}; 각 4-폴리토프의 20개 메트릭스를 에지 길이 단위로 제공하는 귀중한 표.그것들은 단위 반지름의 폴리토페스를 비교하기 위해 대수적으로 변환되어야 한다.
^ Coxeter 1973, 페이지 305, 표 VII: 4차원 일반 화합물.
^ Coxeter 1973, 페이지 12, §1.8 구성.
^ Coxeter 1991, 페이지 30, §4.2.결정체 일반 다상체.
^ Coxeter 1973, 페이지 198–202, §11.7 정규 수치 및 그 줄임말.

참조

T. 고셋:수학의 메신저 맥밀런, 1900년 n차원의 정규 및 반정규격 수치에 관한 연구, 1900년
H.S.M. Coxeter:
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
  - 페이지 120, §7.2. 그림 7.2 참조A을
  - 페이지 296, 표 I(iii):일반 폴리토페스, n-dimension(n≥5)의 일반 폴리토페 3개
- Coxeter, H.S.M. (1991), Regular Complex Polytopes (2nd ed.), Cambridge: Cambridge University Press
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380-407, MR 2,10]
  - (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
  - (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장 409장: 헤미큐브: 1_n1)
Norman JohnsonUniform Polytopes, 원고(1991)
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사 (1966)

외부 링크

Weisstein, Eric W. "Pentatope". MathWorld.
Olshevsky, George. "Pentachoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- 1. 펜타코론에 기초한 볼록한 균일 폴리초라 - 모델1, 조지 올셰프스키
Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o3o - pen".
Der 5-Zeller(5셀) 마르코 뮐러의⁴ R(독일어)에 나오는 일반 폴리토페스
조너선 바우어스, 일반 폴리초라
자바3D 애플릿
화로초론

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	1₂₂ • 2₂₁
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	1₃₂ • 2₃₁ • 3₂₁
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	1₄₂ • 2₄₁ • 4₂₁
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

[elements-1] 5-셀의 5정점은 5개의 4면 세포를 서로 마주보고 있으며, 총 10개의 가장자리와 10개의 삼각면을 가지고 있다.

[polytopes_ordered_by_size_and_complexity-7] 볼록 정규 4폴리탑은 동일한 반지름에 대해 4차원 함량(초대량)의 척도로 크기별로 주문할 수 있다.순서에서 각각의 큰 폴리토프는 동일한 반경 내에 더 많은 내용을^[5] 포함하면서 이전보다 더 둥글다.4심플렉스(5셀)는 한계 최소 케이스, 120셀은 최대 케이스다.복잡성(구성 행렬 또는 정점 수를 비교하여 측정)은 동일한 순서를 따른다.이것은 5 셀이 5 포인트 4 폴리토프인 일반 폴리토페에 대한 대체 숫자 이름 지정 체계를 제공한다: 먼저 600 포인트 4 폴리토프로 이어지는 오름차순으로.

[9] 일반 120 셀은 120개의 일반 도두면체 셀로 구성된 곡선 3차원 경계면을 가지고 있다.또한 120개의 분리형 일반 5셀이 새겨져 있다.^[6]이것들은 3차원 세포가 아니라 120세포의 중심점을 공유하는 4차원 물체로서, 그 정점 600개를 모두 포괄한다.

[13] 4관(tesseract)에는 8개의 3관(tesseract)이 들어 있다(그래서 8세포라고도 한다).각각의 3-큐브는 다른 6개의 튜브에 면접 결합되지만(전적으로 그것을 둘러싸고 있는), 8-셀의 반대편에 놓여 있는 다른 3-큐브와는 완전히 분리된다.

[14] 일반 폴리토프의 경우 생성 특성 정형외과메의 Coxeter-Dynkin 다이어그램은 생성 포인트 링이 없는 생성된 폴리토페의 다이어그램이다.

[15] 치수의 일반 폴리토프의 특성 심플렉스에는 d의 다른 길이의 가장자리가 있고 각 꼭지점에는 각 길이의 가장자리가 하나씩 있다.

[16] 관련된 각도는 일반 심플렉스처럼 60도, 90도뿐이다.

[2] N.W. Johnson: 지오메트리 및 변환, (2018) ISBN978-1-107-10340-5장: 유한대칭군, 11.5 구형 콕시터군, 페이지 249

[3] 마틸라 기카, 예술과 삶의 기하학 (1977), 페이지 68

[FOOTNOTECoxeter1973120§7.2._see_illustration_Fig_7.2<small>A</small>-4] Coxeter 1973, 페이지 120, §7.2. 그림 7.2A를 참조하십시오.

[5] 카테고리 1: 일반 폴리초라

[FOOTNOTECoxeter1973292–293Table_I(ii):_The_sixteen_regular_polytopes_{''p,q,r''}_in_four_dimensions-6] Coxeter 1973, 페이지 292–293, 표 I(ii):4차원의 16개의 일반 폴리토페 {p,q,r}; 각 4-폴리토프의 20개 메트릭스를 에지 길이 단위로 제공하는 귀중한 표.그것들은 단위 반지름의 폴리토페스를 비교하기 위해 대수적으로 변환되어야 한다.

[FOOTNOTECoxeter1973305Table_VII:_Regular_Compounds_in_Four_Dimensions-8] Coxeter 1973, 페이지 305, 표 VII: 4차원 일반 화합물.

[FOOTNOTECoxeter197312§1.8._Configurations-10] Coxeter 1973, 페이지 12, §1.8 구성.

[FOOTNOTECoxeter199130§4.2._The_Crystallographic_regular_polytopes-11] Coxeter 1991, 페이지 30, §4.2.결정체 일반 다상체.

[FOOTNOTECoxeter1973198–202§11.7_Regular_figures_and_their_truncations-12] Coxeter 1973, 페이지 198–202, §11.7 정규 수치 및 그 줄임말.

[a]

[1]

[2]

[3]

[4]

[b]

[c]

[7]

[8]

[9]

[d]

[e]

[f]

[g]

[5]

[6]

슐레플리	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3}	2t{3,3}	tr{3,3}	t_0,3{3,3,3}	t_0,1,3{3,3,3}	t_0,1,2,3{3,3,3}
콕시터
슐레겔

n차원의 숫자 1개_k2
공간	유한한						유클리드 주	쌍곡선
n	3	4	5	6	7	8	9	10
콕시터 무리를 짓다	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉₈⁺ = ${\tilde {E}}_{8}$ ~ ${\tilde {E}}_{8}$ ${\$ ${\tilde {E}}_{8}$ = E	E₁₀ = ${\bar {T}}_{8}$ ${\$ ₈⁺⁺ $}}$ = E
콕시터 도표를 만들다
대칭 (주문)	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[[3^2,2,1]]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
주문	12	120	1,920	103,680	2,903,040	696,729,600	∞
그래프							-	-
이름	1_−1,2	1₀₂	1₁₂	1₂₂	1₃₂	1₄₂	1₅₂	1₆₂

n차원의 2자리_k1 숫자
공간	유한한						유클리드 주	쌍곡선
n	3	4	5	6	7	8	9	10
콕시터 무리를 짓다	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉₈⁺ = ${\tilde {E}}_{8}$ ~ ${\tilde {E}}_{8}$ ${\$ ${\tilde {E}}_{8}$ = E	E₁₀ = ${\bar {T}}_{8}$ ${\$ ₈⁺⁺ $}}$ = E
콕시터 도표를 만들다
대칭	[3^−1,2,1]	[3^0,2,1]	[[3^1,2,1]]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
주문	12	120	384	51,840	2,903,040	696,729,600	∞
그래프							-	-
이름	2_−1,1	2₀₁	2₁₁	2₂₁	2₃₁	2₄₁	2₅₁	2₆₁

{p,3,3}개의 폴리토페스
공간	S³			H³
형태	유한한			파라콤팩트	비컴팩트
이름	{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	...{∞,3,3}
이미지
세포 {p,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{3,3,p}개의 폴리토페스
공간	S³			H³
형태	유한한			파라콤팩트	비컴팩트
이름	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
이미지
꼭지점 형상을 나타내다	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Search

5세포

네임스페이스

더

목차