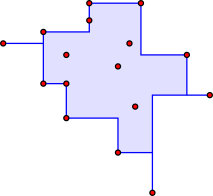
볼록한 선체

기하학에서, 어떤 모양의 볼록 껍질 또는 볼록 외피 또는 볼록 폐색은 어떤 모양을 포함하는 가장 작은 볼록 집합입니다.볼록 선체는 유클리드 공간의 주어진 부분 집합을 포함하는 모든 볼록 집합의 교차로 정의되거나, 부분 집합의 모든 볼록 조합의 집합으로 동등하게 정의될 수 있습니다.평면의 유계 부분집합의 경우, 볼록 선체는 부분집합 주위로 뻗은 고무 밴드로 둘러싸인 형상으로 시각화될 수 있습니다.

오픈 세트의 볼록한 선체는 열려 있고 콤팩트한 세트의 볼록한 선체는 컴팩트합니다.모든 콤팩트 볼록 집합은 극한점의 볼록 선체입니다.볼록 선체 연산자는 폐쇄 연산자의 한 예이며, 이 폐쇄 연산자를 유한한 점 집합에 적용하여 모든 항매트로이드를 나타낼 수 있습니다.평면 또는 다른 저차원 유클리드 공간에서 유한한 점 집합의 볼록 선체를 찾는 알고리즘 문제와 반공간을 교차하는 이중 문제는 계산 기하학의 근본적인 문제입니다.이들은 2차원 또는 3차원 점 집합에 대한 시간 $O{\displaystyle (n}$ ${\displaystyle \log }$⁡ n$$) {\$displaystyle$ O$(n$\log n$)}$에서 풀 수 있으며, 더 높은 차원에서 상한 정리에 의해 주어진 최악의 경우 출력 복잡도와 시간적으로 일치시킬 수 있습니다.

유한한 점 집합뿐만 아니라 볼록 선체도 간단한 다각형, 브라운 운동, 공간 곡선 및 함수의 에피그래프에 대해 연구되었습니다.볼록 껍질은 수학, 통계학, 조합 최적화, 경제학, 기하학, 윤리학 등에 광범위하게 적용됩니다.이와 관련된 구조로는 직교 볼록 선체, 볼록 층, 들라우네 삼각측량 및 보로노이 다이어그램, 볼록 두개골 등이 있습니다.

정의들

유클리드 공간의 점 집합은 각 점 쌍을 연결하는 선분을 포함하는 경우 볼록한 것으로 정의됩니다.주어진 집합 $X$의 볼록 선체$${\$displaystyle X}$는 다음과^[1] 같이 정의될 수 있습니다$$.

1. $X{\displaystyle }$ ${\displaystyle X}$을(를) 포함하는 (고유의) 최소 볼록 집합
2. $X{\displaystyle }$ ${\displaystyle X}$을(를) 포함하는 모든 볼록 집합의 교집합
3. $X{\displaystyle }$ ${\displaystyle X}$의 모든 볼록한 점 조합 집합
4. $X{\displaystyle }$ ${\displaystyle X}$의 정점과 모든 단순의 결합

유클리드 평면에서, 한 선 위의 모든 집합이 아닌 유클리드 평면의 유클리드 집합의 경우, 볼록 $선체$의$경계$는 X {\$displaystyle$ X$}$를 포함하는 최소 둘레를 갖는 단순 폐곡선입니다$.$ $전체{\displaystyle }$ 집합 S ${\displaystyle S}$을 둘러싸도록 고무 밴드를 늘인 다음$$ 풀어서 수축을 허용하는 것을 상상할 수 있습니다. 팽팽해지면 enc$S{\displaystyle }$ ${\displaystyle S}$의 볼록 껍질을 잃습니다$.$^[2] 이 공식은 더 높은 차원으로 즉시 일반화되지 않습니다. 3차원 공간에 있는 유한한 집합의 점들에 대해, 점들의 신장 트리의 이웃이 임의로 작은 표면적, 볼록 껍질의 표면적보다 더 작은 표면적으로 그것들을 에워쌉니다.^[3]그러나, 더 높은 차원에서, 주어진 형상 이상의 최소 에너지 표면을 찾는 장애물 문제의 변형은 볼록 선체를 해결책으로 가질 수 있습니다.^[4]

3차원에 있는 물체의 경우 첫 번째 정의는 볼록 선체가 물체의 가능한 가장 작은 볼록 경계 부피라고 말합니다.볼록 집합의 교차점을 사용하는 정의는 비유클리드 기하학으로 확장될 수 있고, 볼록 조합을 사용하는 정의는 유클리드 공간에서 임의의 실수 벡터 공간 또는 아핀 공간으로 확장될 수 있습니다. 볼록 선체는 또한 더 추상적인 방식으로, 배향된 매트로이드로 일반화될 수 있습니다.^[5]

정의 등가성

첫 번째 정의가 일리가 있다는 것은 명확하지 않습니다. 모든 $X{\displaystyle }$ ${\displaystyle X}$에 $대해$X ${\displaystyle X}$을(를) 포함하는 고유한 최소 볼록 집합이 존재해야 하는 이유는 무엇입니까$?$ 그러나 두 $번째{\displaystyle }$ 정의인$$X {\$displaystyle X}$을(를) 포함하는 모든 볼록 집합의 교집합은$$잘 정의되어 있습니다.$Y{\displaystyle }$ ${\displaystyle Y}$이(가) 교차하는 집합에 포함되어 있기$$ 때문에$$$X{\displaystyle }${\$displaystyle X}$을(를) 포함하는$$ 다른 모든 볼록 집합 $Y{\displaystyle }$ ${\displaystyle Y}$의 부분 집합입니다.따라서 $X{\displaystyle }$ ${\displaystyle$ X$}$을(를) 포함하는 고유한 최소 볼록 집합입니다$.$ 따라서 처음 두 정의는 같습니다.^[1]

$X{\displaystyle }$ ${\$$displaystyle X}$를 포함하는 각 볼록 집합은 (볼록하다는 가정에 의해) X {\$displaystyle X}$의 점들의 모든 볼록 조합을 포함해야 하므로$$$,$ 모든 볼록 조합의 집합은 $X{\displaystyle }$ ${\displaystyle$ X$}$를 포함하는 모든 볼록 집합의 교집합에 포함됩니다$.$ 반대로, 모든 볼록 조합의 집합은 그 자체로 볼록 집합입니다$X{\displaystyle }$ ${\displaystyle X}$을$($를) 포함하므로$$X {\$displaystyle X}$을(를) 포함하는 모든 볼록 집합의 교집합도 포함하므로$$두 번째 정의와 세 번째 정의는 같습니다.^[6]

사실, 카라테오도리의 정리에 따르면, $X{\displaystyle }$ ${\displaystyle X}$가 d ${\displaystyle d}$차원$$ 유클리드 공간의 부분 집합이라면$$, $X{\displaystyle }$ ${\displaystyle X}$의 유한한 많은 점들의 모든 볼록 조합도$$ $X{\displaystyle }$ ${\displaystyle X}$의 최대 $d{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle d+1}$ 점들의$$ 볼록 조합입니다$.$$({\displaystyle d}$+ ${\displaystyle 1)}$ ${\displaystyle (d+1)}$ - 점의$$ 몇 개의 볼록한 조합의 집합은 심플렉스입니다. 평면에서는 삼각형이고 3차원 공간에서는 사면체입니다.따라서 $X{\displaystyle }$ ${\displaystyle X}$의 점들의 모든 볼록 조합은 $정점들$이$$X {\$displaystyle$ X$}$에 속하는 심플렉에 속하며$$$,$ 세 번째 정의와 네 번째 정의는 같습니다.^[6]

상부 선체 및 하부 선체

볼록한 선체는 2차원적으로 상부 선체와 하부 선체의 두 부분으로 분할되어 선체의 최좌측 지점과 우측 지점 사이로 확장되기도 합니다.일반적으로, 어떤 차원에서든 볼록 선체의 경우, 선체의 경계를 상향-대향 지점(상향 광선이 선체와 분리된 지점), 하향-대향 지점 및 극단 지점으로 분할할 수 있습니다.3차원 선체의 경우, 경계면의 위쪽을 향하는 부분과 아래쪽을 향하는 부분이 위상 디스크를 형성합니다.^[7]

위상속성

닫힌 선체와 열린 선체

집합의 닫힌 볼록 선체는 볼록 선체의 폐쇄이고, 열린 볼록 선체는 볼록 선체의 내부(또는 일부 소스에서 상대적인 내부)입니다.^[8]

$X{\displaystyle }$ ${\displaystyle X}$의 닫힌 볼록 선체는 $X{\displaystyle }$ ${\displaystyle X}$를 포함하는 모든 닫힌 반공간의 교차점입니다$.$ $만약{\displaystyle }$ X ${\displaystyle X}$의 볼록 선체가 이미 닫힌 집합 그 자체라면$$(예를 들어, $X{\displaystyle }$ ${\displaystyle X}$가 유한 집합이거나 더 일반적으로 콤팩트 집합이라면), 그것은 닫힌 볼록 선체와 같습니다.그러나 닫힌 반공간의 교차점은 그 자체로 닫혀 있으므로 볼록한 선체가 닫혀 있지 않을 때는 이런 식으로 표현할 수 없습니다.^[9]

집합 $X{\displaystyle }$ ${\displaystyle X}$의 열린 볼록 선체가 $d{\displaystyle }$ ${\displaystyle d}$차원이면$$$$ 선체의 모든 점은 $X{\displaystyle }$ ${\displaystyle X}$의 최대 ${\displaystyle \mathrm{2d}}$ ${\displaystyle 2d}$점의$$ 열린 볼록 선체에 속합니다$.$정사각형, 정팔면체 또는 고차원 교차 다각형의 꼭짓점 집합은 정확히 $2{\displaystyle \mathrm{}}$ ${\displaystyle d}$ ${\displaystyle 2d}$ 점이$$ 필요한 예를 제공합니다.^[10]

위상학적 특성 보존

위상학적으로, 개방형 집합의 볼록한 선체는 항상 열려 있고, 콤팩트한 집합의 볼록한 선체는 항상 그 자체로 콤팩트한 집합의 볼록한 선체는 항상 그 자체입니다.그러나 볼록한 선체가 닫히지 않는 닫힌 집합이 존재합니다.^[11]예를 들어, 닫힌 집합은

${\displaystyle \left\{(x,y)\mathop {\bigg } y\geq {\frac {1}{1+x^{2}}}\right\}}$

(아그네스시의 마녀 위 또는 위쪽에 있는 점들의 집합)은 위쪽의 반평면이 볼록한 선체로 되어 있습니다.^[12]

유한 차원 유클리드 공간에서 콤팩트 집합의 볼록 선체의 콤팩트성은 크레인-스물리안 정리에 의해 일반화되며, 이에 따라 바나흐 공간의 약한 콤팩트 부분 집합(약한 위상 아래에서 콤팩트한 부분 집합)의 닫힌 볼록 선체는 약한 콤팩트합니다.^[13]

익스트림 포인트

볼록 집합의 극단점은 집합 내에서 동일한 집합의 다른 두 점 사이에 있는 열린 선 세그먼트에 놓이지 않는 점입니다.볼록 선체의 경우, 모든 극한점은 주어진 집합의 일부여야 합니다. 그렇지 않으면 주어진 점들의 볼록한 조합으로 형성될 수 없기 때문입니다.크레인-밀만 정리에 따르면, 유클리드 공간(또는 더 일반적으로 국소 볼록 위상 벡터 공간)에 있는 모든 콤팩트 볼록 집합은 그 극한점의 볼록 선체입니다.^[14]그러나, 이것은 콤팩트하지 않은 볼록 집합의 경우에는 성립하지 않을 수 있습니다. 예를 들어, 전체 유클리드 평면과 열린 단위 공은 모두 볼록하지만, 둘 다 극단적인 점이 없습니다.초케 이론은 이 이론을 극한점의 유한 볼록 조합에서 더 일반적인 공간의 무한 조합(적분)까지 확장합니다.^[15]

기하학적 및 대수적 성질

폐쇄 연산자

볼록-헐 연산자는 폐쇄 연산자의 특성을 갖습니다.^[16]

• 이는 $모든{\displaystyle }$ 집합$$X {\$displaystyle$X}의 볼록 $선체$가$$X {\$displaystyle$ X$}$의 수퍼세트라는$$ 것을 의미하는 광범위합니다$.$
• 감소하지 않음은 $X$ ⊆ ${\displaystyle Y}$가 ${\displaystyle X}$인 $X$ ${\$displaystyle X$}$ 및 $Y$ ${\$$displaystyle$ $Y}$ 두 집합에 대해$$$X$ ${\displaystyle X}$의 볼록 껍질은 $Y$ ${\displaystyle Y}$의 볼록 껍질의 부분 집합임을 의미합니다$.$
• 이는 $모든{\displaystyle }$X {\$displaystyle X}$에 $대해{\displaystyle }$X {\$displaystyle$X}의 볼록 $선체$가$$X {\$displaystyle$X}의 볼록 선체와 동일하다는$$것을 의미하는 idempotent입니다$.$

유한한 점 집합에 적용할 경우, 이는 점 집합의 셸링 안티매트로이드인 안티매트로이드의 폐쇄 연산자입니다.모든 반매트로이드는 충분히 높은 차원의 유클리드 공간에서 볼록한 점 선체에 의해 이러한 방식으로 표현될 수 있습니다.^[17]

민코프스키 합

볼록 선체를 구성하고 민코프스키 합을 취하는 작업은 집합의 볼록 선체의 민코프스키 합이 동일 집합의 민코프스키 합의 볼록 선체와 동일한 결과를 준다는 점에서 서로 통근합니다.이것은 볼록한 선체로부터 민코프스키 합의 거리를 제한하는 샤플리-포크먼 정리를 향한 단계를 제공합니다.^[18]

투영 이중성

점 집합의 볼록 선체를 구성하기 위한 투영 이중 연산은 원점(또는 다른 지정된 점)을 모두 포함하는 닫힌 반공간 패밀리의 교차점을 구성하는 것입니다.^[19]

특수한 경우

유한 점 집합

유한 점 집합 $S$ ⊂ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle S\subset \mathbb {R}^{d}}$의 볼록 선체는 $d$ = ${\displaystyle 2}$ ${\displaystyle$d=$2}$일 때 볼록 다각형을 형성하며$,$ 더 일반적으로는 R ${\displaystyle {}^{}}$ ${\displaystyle \mathbb {R}^{d}$일 때 볼록 다각형을 형성합니다$.$ 선체의 각 극단점을 정점이라고 합니다.(크레인-밀만 정리에 의해) 모든 볼록 다포체는 꼭짓점의 볼록 껍질입니다.$꼭짓점$이$$S {\$displaystyle S}$에 속하고$$ $S{\displaystyle }$ ${\displaystyle S}$를 모두 둘러싸는 유일한 볼록 다포체입니다$.$^[2] 일반 위치의 점 집합에서 볼록 껍질은 단순 다포체입니다.^[20]

상한 정리에 따르면, $d$ ${\displaystyle d}$ - 차원 유클리드 공간에서 $n$ ${\displaystyle n}$ 점의 볼록 선체의 면의 $수$는 O${\displaystyle (n^{}}$ ⌊ ${\displaystyle d^{}}$/ 2 ⌋${\displaystyle {}^{}}${\$displaystyle$ O$(n^{\lfloor d/2\rfoor$})}이며$,$ 특히 2차원과 3차원에서 면의 수는 $n$ ${\displaystyle n}$에서 최대 선형입니다$.$

단순다각형

단순 다각형의 볼록한 선체는 주어진 다각형을 감싸고, 그것에 의해 영역으로 분할되며, 그 중 하나가 다각형 자체입니다.다각형의 다각형 사슬과 단일 볼록한 선체 가장자리로 경계를 이루는 다른 영역은 주머니라고 불립니다.각 포켓에 대해 동일한 분해를 재귀적으로 계산하면 볼록 차이 트리라고 하는 주어진 다각형에 대한 계층적 설명을 형성합니다.^[23]주머니를 볼록한 선체 가장자리에 반사시키면 주어진 단순 다각형이 동일한 둘레와 더 큰 면적을 가진 다각형으로 확장되며, 에르트 ő스-나기 정리는 이 확장 과정이 결국 종료된다는 것을 나타냅니다.

브라운 운동

평면에서 브라운 운동에 의해 생성된 곡선은 임의의 고정된 시간에 경계가 연속적으로 미분 가능한 곡선을 형성하는 볼록한 선체를 가질 확률이 1입니다.그러나 범위 π/ <θ <π ${\displaystyle$\$theta }$의 각도 θ$${\displaystyle \$pi /2<\theta <\pi }$에 대해서는 브라운 운동 중에 움직이는 입자가 각도 θ ${\displaystyle \theta }$에서 볼록한 선체의 경계에 닿는 경우가 있습니다$.$ 이 예외적인 시간 집합의 하우스도르프 차원은 (높은 pr로)obility$)$ 1 -${\displaystyle }$π / 2${\displaystyle }$θ ${\displaystyle$ 1-$\pi$ / 2$\theta}.$

공간 곡선

공간 곡선의 볼록 선체 또는 3차원 공간의 일반 위치에 있는 공간 곡선의 유한 집합의 경우, 곡선에서 떨어진 경계 부분은 전개 가능하고 지배된 표면입니다.^[26]예를 들면, 오로이드, 수직면에서 두 개의 원으로 이루어진 볼록한 선체, 두 개의 원으로 이루어진 볼록한 선체, ^[27]구면, 두 개의 반원으로 이루어진 볼록한 선체, 그리고 두 개의 반원으로 이루어진 볼록한 선체가 서로 같은 중심을 가진 수직면에서 각각 통과하는 D형,동일한 둘레의 평면 볼록 집합 두 개를 서로 붙여서 형성된 표면에 대한 알렉산드로프의 유일성 정리에서 얻은 볼록 형상.^[28]

기능들

실벡터 공간 상의 함수$$$f{\displaystyle }$ {\$displaystyle f}$의 볼록 선체 또는 하부 볼록 포락선은, $에픽$이$$f {\$displaystyle f}$의 에픽의 하부 볼록 선체인 함수인$,$ $f{\displaystyle }$ ${\displaystyle f}$로 대수화된 고유 최대 볼록 함수$.$^[29]정의는 함수 집합의 볼록 선체로 확장될 수 있으며(그들의 비문 결합의 볼록 선체에서 얻거나 또는 점별 최소값에서 동등하게 얻음), 이 형태에서 볼록 켤레 연산과 이중입니다.^[30]

계산

계산 기하학에서, 유한한 점 집합과 다른 기하학적 객체에 대해 볼록 선체를 계산하는 많은 알고리즘이 알려져 있습니다.볼록 선체를 계산한다는 것은 필요한 볼록 형상의 모호하지 않고 효율적인 표현을 구성한다는 것을 의미합니다.점 집합의 볼록 선체에 대해 고려된 출력 표현에는 선체의 면을 설명하는 선형 부등식 목록, 면과 그 인접성의 무방향 그래프 또는 선체의 전면 격자가 포함됩니다.^[31]2차원에서는 선체를 중심으로 정점인 점을 순환 순서대로 나열하는 것으로 충분할 수 있습니다.^[2]

2차원 또는 3차원의 볼록 선체의 경우, 대응하는 알고리즘의 복잡도는 $일반적$으로 n$${\$displaystyle$ n$\},$ 입력 지점의 수$,$ $h{\displaystyle }$ ${\displaystyle h},$ 그리고 $n{\displaystyle }$ ${\displaystyle n}$보다 상당히 작을 수 있는 볼록 선체의 점의 수로 추정됩니다$.$다른 차원의 면의 개수도 분석에 포함될 수 있습니다.그레이엄 스캔은 평면에서 $n개$의 ${\displaystyle$ n$}$개 $지점$의 볼록 선체를 시간 O(${\displaystyle n}$ $로그$$$⁡ ${\displaystyle n}$${\displaystyle )}$ {\$displaystyle O(n\log$ $n$$)}$에 $계산$할 수 있습니다$.$ 2차원 및 3차원 지점의 경우, 시간 O(${\displaystyle n}$ ${\displaystyle \mathrm{로그}}$ ⁡ h${\displaystyle O$ h$)}$에 볼록 선체를 계산하는 더 복잡한 출력 민감 알고리즘이 알려져 있습니다.여기에는 Chan의 알고리즘과 Kirkpatrick-Seidel 알고리즘이 포함됩니다.^[32]차원 > ${\displaystyle d>3}$의 경우 볼록 선체를 계산하는 시간은 O${\displaystyle {}^{}}$⌊ ${\displaystyle d^{}}$/ ${\displaystyle 2^{}}$ ⌋)${\displaystyle O(n^{\lfloor d/2\rfoor })$로$$문제의 최악의 경우 출력 복잡도와 일치합니다.평면에서 단순 다각형의 볼록 선체는 선형 시간으로 구성할 수 있습니다.^[34]

동적 볼록 선체 데이터 구조는 점들의 삽입 및 삭제가 진행되는 일련의 점들의 볼록 선체를 추적하기 위해 사용될 수 ^[35]있고, 동적 볼록 선체 구조는 점들이 연속적으로 움직이는 것에 대해 볼록 선체를 추적할 수 있습니다.^[36]볼록 선체의 구성은 또한 점 세트의 폭과 직경을 계산하기 위한 회전 캘리퍼 방법과 같은 다른 많은 계산-기하학적 알고리즘의 구성 요소인 도구의 역할을 합니다.^[37]

관련 구조물

볼록 선체와 유사한 방식으로 점 집합에서 몇 가지 다른 모양을 정의할 수 있습니다. 어떤 성질을 가진 최소 초집합, 주어진 모양 집합에서 점을 포함하는 모든 모양의 교집합 또는 특정 유형의 조합에 대한 모든 점 조합의 결합입니다.예를 들어 다음과 같습니다.

• 아핀 선체는 주어진 집합을 포함하는 유클리드 공간의 가장 작은 아핀 부분 공간 또는 집합의 모든 아핀 조합의 집합입니다.^[38]
• 선형 선체는 주어진 집합을 포함하는 벡터 공간의 가장 작은 선형 부분공간 또는 집합 내의 모든 점들의 선형 조합입니다.^[38]
• 벡터 공간의 부분 집합의 원뿔 선체 또는 양의 선체는 부분 집합의 모든 양의 점 조합의 집합입니다.^[38]
• 시점 집합에 대한 3차원 객체의 시각 선체는 시점에서 $p{\displaystyle }$ ${\displaystyle$ p$}$까지의 모든 광선이 객체와 교차하도록$$$$ 점 $p{\displaystyle }${\$displaystyle$ p$}$로 구성됩니다.이와 동등하게 각 시점에 대한 객체의 윤곽에 의해 생성된 (비볼록) 원뿔의 교차점입니다.주어진 관점에서 동일한 윤곽을 가질 수 있는 가장 큰 형상으로 3D 재구성에 사용됩니다.^[39]
• 평면 부분 집합의 원형 선체 또는 알파 선체는 부분 집합을 포함하는$$ 주어진 반지름이${\displaystyle }$1 / ${\displaystyle \alpha }$ ${\displaystyle 1/\alpha}$인 모든 디스크의 교차점입니다.^[40]
• 2차원 단순 다각형의 부분집합의 상대적 볼록 선체는 모든 상대적 볼록 초집합의 교집합이며, 동일한 다각형 내의 집합은 점들 중 임의의 두 점 사이에 측지선을 포함하는 경우 상대적으로 볼록합니다.^[41]
• 직교 볼록 선체(orthogonal convex hull) 또는 직선 볼록 선체(rightlinear convex hull)는 모든 직교 볼록 및 연결 초집합의 교차점이며, 집합이 점 쌍 사이의 모든 축-평행 세그먼트를 포함하는 경우에는 직교 볼록입니다.^[42]
• 직교 볼록 선체는 훨씬 더 일반적인 구조인 하이퍼 볼록 선체의 특별한 경우로, 주어진 메트릭 공간의 점을 포함하는 가장 작은 주입 메트릭 공간으로 간주될 수 있습니다.^[43]
• 동형 볼록 선체는 주어진 집합을 포함하는 동형 함수의 하위 집합의 교집합으로 구한 복잡한 해석 다양체와 유사한 개념의 일반화입니다.^[44]

점 집합의 들라우네 삼각형과 그 쌍대인 보로노이 다이어그램은 볼록 선체와 수학적으로 관련이 있습니다. ${\displaystyle {}^{}}$ ${\$에 설정된 점의 들라우네 삼각형은 ${\displaystyle {}^{}}$ ${\displaystyle {+}^{}}$ ${\displaystyle 1^{}}$의 볼록 선체의 투영으로 볼 수 있습니다$$${\displaystyle {}^{}}$ ${\displaystyle \mathbb {R}^{n+1}}$$$^[45] 유한 점 집합의 알파 모양은 다양한 수준의 세부 정보에서 점 집합의 모양을 설명하는 중첩된 (비볼록) 기하 객체 패밀리를 제공합니다.각각의 알파 모양은 들라우네 삼각형의 일부 특징들의 결합이며, 그들의 원반지름을 매개변수 알파와 비교함으로써 선택됩니다.점 집합 자체는 이 도형 계열의 한 끝점을 형성하고, 볼록한 선체는 다른 끝점을 형성합니다.^[40]점 집합의 볼록 층은 볼록 다각형의 중첩된 패밀리이며, 가장 바깥쪽은 볼록 선체이며, 내층은 볼록 선체의 꼭짓점이 아닌 점으로부터 재귀적으로 구성됩니다.^[46]

다각형의 볼록한 두개골은 그 안에 들어있는 가장 큰 볼록한 다각형입니다.다항식 시간에 찾을 수 있지만 알고리즘의 지수가 높습니다.^[47]

적용들

볼록한 선체는 많은 분야에서 광범위하게 사용됩니다.수학에서 볼록 선체는 다항식, 행렬 고유값 및 단일 요소를 연구하는 데 사용되며 이산 기하학의 여러 정리에는 볼록 선체가 포함됩니다.이들은 견고한 통계량에서 Tukey 깊이의 가장 바깥쪽 윤곽선으로 사용되며, 2차원 데이터의 백플롯 시각화의 일부이며, 무작위 결정 규칙의 위험 집합을 정의합니다.조합 문제에 대한 솔루션의 지시 벡터의 볼록 선체는 조합 최적화 및 다면체 조합론의 중심입니다.경제학에서 볼록 껍질은 경제학에서 볼록하지 않은 시장에 볼록한 방법을 적용하는 데 사용될 수 있습니다.기하학적 모델링에서 볼록 선체 특성 베지어 곡선은 교차점을 찾는 데 도움이 되며, 볼록 선체는 보트 선체 측정의 일부입니다.그리고 동물의 행동에 대한 연구에서 볼록한 선체는 가정 범위의 표준 정의로 사용됩니다.

수학

일변량 다항식의 뉴턴 다각형과 다변량 다항식의 뉴턴 다각형은 다항식의 항 지수에서 파생된 점의 볼록 선체이며 다항식의 점근적 거동과 그 근의 값을 분석하는 데 사용될 수 있습니다.^[48]볼록 선체와 다항식은 가우스-루카스 정리에서도 함께 나오는데, 이에 따르면 다항식의 도함수의 근은 모두 다항식의 근의 볼록 선체 안에 있습니다.^[49]

스펙트럼 분석에서 정규 행렬의 수치 범위는 고유 값의 볼록 선체입니다.^[50]루소-다이 정리는 C*대수형에서 단위 원소의 볼록한 선체를 설명합니다.^[51]이산 기하학에서, 라돈의 정리와 트베르그의 정리는 서로 교차하는 볼록한 선체를 가진 부분집합으로 이루어진 점 집합의 분할의 존재와 관련이 있습니다.^[52]

점 사이에 선분을 포함하는 볼록 집합과 모든 볼록 초집합의 교집합인 볼록 선체의 정의는 쌍곡 공간뿐만 아니라 유클리드 공간에도 적용됩니다.그러나 쌍곡 공간에서는 쌍곡 공간 자체에 속하지 않고 해당 공간의 모델 경계에 있는 점인 이상적인 점들의 볼록 선체를 고려할 수도 있습니다.3차원 쌍곡 공간의 이상적인 점의 볼록 선체 경계는 유클리드 공간의 지배 표면과 유사하며, 그들의 메트릭 특성은 저차원 위상에서 기하학 추측에 중요한 역할을 합니다.^[53]쌍곡 볼록 선체는 또한 쌍곡 다양체의 표준 삼각측량 계산의 일부로 사용되었으며, 매듭의 등가성을 결정하는 데 적용되었습니다.^[54]

볼록한 선체를 이 주제에 적용하기 위한 브라운 운동에 대한 부분과 전개 가능한 표면 이론에 적용하기 위한 공간 곡선에 대한 부분도 참조하십시오.

통계

강건 통계학에서 볼록 껍질은 2차원 표본 점의 퍼짐을 시각화하는 방법인 백플롯의 주요 구성 요소 중 하나를 제공합니다.Tukey 깊이의 등고선은 볼록 껍질이 가장 바깥쪽에 있는 중첩 볼록 집합 패밀리를 형성하며, 백 플롯은 이 중첩 패밀리의 또 다른 다각형인 50% 깊이의 등고선도 표시합니다.^[55]

통계적 의사결정이론에서, 무작위 의사결정 규칙의 위험 집합은 기본적인 결정론적 의사결정 규칙의 위험점의 볼록한 선체입니다.^[56]

조합 최적화

조합 최적화 및 다면체 조합론에서 연구의 중심 대상은 조합 문제에 대한 솔루션의 지시 벡터의 볼록 선체입니다.폴리토페를 반공간의 교차점으로 설명하여 이러한 폴리토페의 측면을 찾을 수 있다면 선형 프로그래밍에 기초한 알고리즘을 사용하여 최적의 솔루션을 찾을 수 있습니다.^[57]다중 목적 최적화에서는 다른 유형의 볼록 선체, 즉 솔루션의 무게 벡터의 볼록 선체도 사용됩니다.각각의 볼록한 선체 꼭짓점을 찾아 확인함으로써, 종종 모든 가능한 해를 확인하는 것보다 더 효율적으로 무게의 준 볼록 조합을 최대화할 수 있습니다.^[58]

경제학

일반적인 경제 균형의 화살표-데브레우 모형에서 대리인은 볼록한 예산 집합과 볼록한 선호도를 가진다고 가정합니다.경제학에서 볼록성에 대한 이러한 가정은 평형의 존재를 증명하는 데 사용될 수 있습니다.실제 경제 데이터가 비볼록일 때, 볼록한 선체를 취하여 볼록하게 만들 수 있습니다.샤플리-포크먼 정리를 사용하여 대규모 시장의 경우 이 근사치가 정확하며 원래의 비볼록 시장에 대해 "준평형"으로 이어짐을 보여줄 수 있습니다.^[59]

기하학적 모델링

기하학적 모델링에서 베지어 곡선의 주요 특성 중 하나는 제어점의 볼록한 선체 안에 있다는 것입니다.이 소위 "볼록 선체 특성"은 예를 들어, 이러한 곡선들의 교차점들을 신속하게 검출하는데 사용될 수 있습니다.^[60]

체인 둘레(chain girth)는 선박과 선박 설계의 기하학에서 선박의 선체 단면의 볼록한 선체를 사용하여 정의된 항해 선박의 크기를 측정하는 것입니다.선체가 볼록한 배와 배를 제외하고는 단면의 둘레인 피부 둘레와는 다릅니다.^[61]

윤리학

볼록 껍질은 동물의 행동을 연구하는 동물 행동학에서 최소 볼록 다각형으로 흔히 알려져 있는데, 동물이 관찰된 지점을 기반으로 동물의 서식 범위를 추정하는 고전적이지만 단순한 접근법입니다.^[62]이상치는 최소 볼록 다각형을 지나치게 크게 만들 수 있으며, 이는 예를 들어 표본의 목표 백분율에 가까운 볼록 층 중 하나를 선택하거나 ^[63]점 이웃의 볼록 선체를 결합하여 국부 볼록 선체 방법에서 관측치의 부분 집합만 포함하는 완화된 접근 방식에 동기를 부여합니다.^[64]

양자물리학

양자물리학에서, 모든 양자계의 상태 공간(계가 준비될 수 있는 모든 방법의 집합)은 극한점이 순수 상태로 알려져 있고 내부점이 혼합 상태라고 불리는 양의 반정미적 연산자인 볼록 선체입니다.^[65]슈뢰딩거-HJW 정리는 실제로 어떤 혼합 상태도 다양한 방법으로 순수한 상태의 볼록한 조합으로 작성될 수 있음을 증명합니다.^[66]

열역학

Josiah Willard Gibbs (1873)는 열역학에서 볼록한 선체를 발견했지만,^[68] 이 논문은 볼록한 선체의 이름이 그렇게 지어지기 전에 발표되었습니다.물질의 몇 가지 화학양론계 에너지 집합에서는 하부 볼록 선체에서의 측정값만 안정적입니다.선체에서 점을 제거한 후 선체와의 거리를 계산할 때, 새로운 선체와의 거리는 위상의 안정성 정도를 나타냅니다.^[69]

역사

평면에 있는 점들의 아래 볼록한 선체는 뉴턴 다각형의 형태로 아이작 뉴턴이 헨리 올덴부르크에게 1676년 보낸 편지에 나타납니다.^[70]"볼록 선체"라는 용어 자체는 Garrett Birkhoff(1935)의 연구 초기에 등장하며, 독일어로 대응되는 용어는 예를 들어 Hans Rademacher의 K ő닉(1922)의 리뷰에서 일찍이 등장합니다."볼록 포락선"과 같은 다른 용어들도 이 시간대에 사용되었습니다.^[71]1938년까지 Lloyd Dines에 따르면, "볼록 선체"라는 용어가 표준이 되었다고 합니다; Dines는 "볼록 선체"라는 단어의 구어적 의미가 그것이 형상의 표면을 가리킨다는 것을 암시하는 반면, 볼록 선체는 표면만이 아닌 내부를 포함한다는 것을 암시하기 때문에, 그 용어가 유감스럽게 생각한다고 덧붙였습니다.^[72]

메모들

참고문헌

외부 링크

• "Convex hull", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W., "Convex Hull", MathWorld
• 에릭 W의 "Convex Hull" Weisstein, Wolfram 데모 프로젝트, 2007.