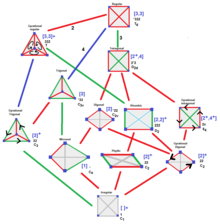
구성(폴리토프)

기하학에서 H. S. M. Coxeter는 일반 폴리토프를 특별한 종류의 구성이라고 불렀다.

기하학의 다른 구성들은 뭔가 다르다.이러한 폴리토프 구성은 발생 행렬이라고 더 정확하게 불릴 수 있으며, 여기서 유사한 요소들이 행과 열에 함께 수집된다.일반 폴리탑은 k-face 요소당 하나의 행과 열을 가지며, 다른 폴리탑은 대칭 등급별로 k-face 유형별로 하나의 행과 열을 가진다.대칭이 없는 폴리토프는 모든 원소에 대해 하나의 행과 열을 가지며, 원소가 연결되지 않으면 행렬이 0, 연결되면 1로 채워진다.동일한 k의 요소는 연결되지 않으며 "*" 테이블 항목이 있다.^[1]

모든 폴리토프, 추상적인 폴리토프에는 이러한 연관성을 나타내는 하세 도표가 있는데, 이것은 발생 행렬로 체계적으로 설명할 수 있다.

일반 폴리탑에 대한 구성 매트릭스

일반 폴리토프에 대한 구성은 대각선 요소 N이_i 폴리토프의 i-faces 수인 매트릭스로 표현된다.대각선 원소는 폴리토프의 f-벡터라고도 불린다.비대각(i ≠ j) 요소 N은_ij 각 i-face 요소와 충돌하는 j-faces의 수입니다. 그래서 NN_i_ij = NN_j_ji.^[2]

원리는 일반적으로 $n차원$ 으로 확장되며, $여기$ 서 0 $j$ j < $n$ .

{\display{bmatrix}{\display{bmatrix}{N_{0}&N_{0,1}&N_{0,2}&\cdots &N_{0,n-1}\\N_{1,0}&N_{1}&N_{1,2}&\cdots &N_{1,n-1}\\\vdots &\vdots &\vdots &&\vdots \\N_{n-1,0}&N_{n-1,1}&N_{n-1,2}&\cdots &N_{n-1}\end{matrix}}\end{bmatrix}}

폴리곤

일반 폴리곤, Schléfli 기호 {q}은(는) 2x2 행렬을 가지며, 정점의 경우 첫 번째 행, 가장자리의 경우 두 번째 행이 있다.주문 g는 2q 입니다.

{\display{bmatrix}{\display{bmatrix}{N_{0}&N_{01}\\N_{10}&N_{1}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2&2\\2&g/2\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}q&2\\2&q\end{matrix}}\end{bmatrix}}

일반 n-곤은 2n x 2n 행렬을 가지며, 첫 번째 n행과 열 정점, 마지막 n행과 열을 가장자리로 한다.

삼각형 예제

삼각형에는 등각형, 이소체, 스칼렌의 세 가지 대칭분류가 있다.이들은 모두 동일한 발생 행렬을 가지고 있지만, 대칭성을 통해 정점과 가장자리를 함께 수집하고 계수할 수 있다.이들 삼각형에는 A,B,C, 에지 a,b,c라는 정점이 있고, 대칭 연산에 의해 서로 매핑될 수 있는 정점과 에지는 동일한 라벨이 붙어 있다.

삼각형

등각형
{3}

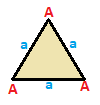Equilateral triangle element-labeled.png

이소셀레스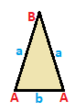
{ }∨( )

스칼렌
( )∨( )∨( )

(v:3; e:3)

(v:2+1, e:2+1)

(v:1+1+1; e:1+1+1)

A -+++++++++++++++++++++++++++++++++++

A B a b --+-----++- A 2 * 1 B * 1 1 B * 1 2 0 --+-----+------ 1 1 2 * 2 * 0 * 1

A B C a b c --+------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1

사변측정감시

대칭에 의한 사변측정감시

사방측정감시선은 각각 고유한 행렬을 가진 대칭에 의해 분류될 수 있다.사분면 측정은 동일한 행렬을 가진 180도 회전하고 정점과 가장자리가 역전되는 이중 쌍을 가지고 있다.정사각형과 병렬형 및 일반 사분면 측정은 등급별로 자가 이중화되므로 180도 회전 시 행렬이 변경되지 않는다.

사변측정감시
사각형 {4}	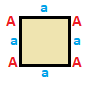직사각형 { }×{ }	마름모꼴 { }+{ }	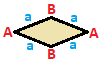평행사변형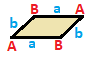
(v:4; e:4)	(v:4; e:2+2)	(v:2+2; e:4)	(v:2+2; e:2+2)
A -+++++++++++++++++++++++++++++++++++	A b -+------------------------------------------------------------------------------------------------------------------------------------2 * 2	A B a -+-----+---------------------------------------------------------------------------------------------------------------------- 1 1 1 4	A B a b -+-----++- A 2 * 1 B * 1 B * 2 1 - 1 -+-++----- 1 2 - 1 2
이소셀 사다리꼴 { } { }	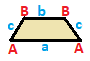연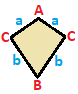	일반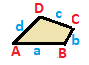
(v:2+2; e:1+1+2)	(v:1+1+2; e:2+2)	(v:1+1+1+1; e:1+1+1+1)
A B a b c --+++++------- A 2 * 1 0 1 B * 2 0 1 --++++---------- 2 0 1 * 2 0 1 * 0 2 * 0 2 * 1 * 1 * 1 * 1 * 2	A B C a b -+----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------	A B C D a b c d --+------------------------------------------------------ A 1 * 1 0 1 B * 1 0 0 C * 1 * 1 0 0 0 D * * 1 0 D * * 1 0 0 D * * 1 0 1 * * 0 0 0 0 * 0 0 0 0 * 0 0 0 * 0 0 0 * 0 0 0 * 0 0 * 0 0 0 0 * 1 * * * * * * 0 0 0 0 0 * 0 * 0 * 0 * 0 0 0 0 * 0 * * * * * 0 * 0 * 0 * 0 * * 0 * * 0 * 0 * * * * * * * * * * *

복합 다각형

이 아이디어는 C $\mathbb {C} ^{2}$ ${\$ :로 구성된 일반 복합 폴리곤에도 적용할 _r수 있다.

{\display{bmatrix}{\display{bmatrix}{N_{0}&N_{01}\\N_{10}&N_{1}\end{bmatrix}\end{bmatrix}={\begin{bmatrix}{begin{bmatrix}{g&r\\p&g\end{bmatrix}}}}}}

복합반사군은 [q],_r $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ g $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ = 8 $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ + 2 $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ + $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ r $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ - $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ 1 $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ ) - $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ ${\$ g= $8/q\cdot (1/p+2/q+1/r-1)^{-2$ ^[3]^[4]

폴리헤드라

각 j-공간이 $N jk$ k-spaces $(j$ ≠ $k$ )와 충돌하는 지점, 선, 평면 또는 j-spaces $(0$ ≤ $j$ < 3)의 발생을 고려해 3차원으로 아이디어를 적용할 수 있다 $.$ 존재하는 j-spaces 수에 $대해 j$ N을 쓰는 경우, 주어진 구성은 매트릭스로 나타낼 수 있다.

{\

N_{0}&N_{01}&N_{02}\\

N_{10}&N_{1}&N_{12}\\

N_{20}&N_{21}&N_{2}\end{matrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{matrix}g/2q&q&q\\2&g/4&2\\p&p&g/2p\end{matrix}}\end{bmatrix}}}

for Schläfli symbol {p,q}, with group order g = 4pq/(4 − (p − 2)(q − 2)).

사면체

사면체의 대칭

테트라헤드라는 대칭에 따라 그룹화할 수 있는 행렬을 가지고 있으며, 일반 사면체는 4개의 정점, 6개의 가장자리, 4개의 면에 대해 14개의 행과 열을 가지고 있다.테트라헤드라는 자가이중이며, 매트릭스를 180도 회전(정점 및 면 교환)하면 변경되지 않는다.

테트라헤드라속

정규
(v:4; e:6; f:4)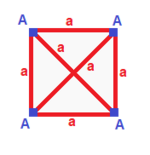

사방형 분산형
(v:4; e:2+4; f:4)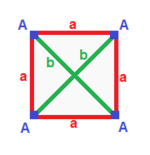

롬빅 디페노이드
(v:4; e:2+2+2; f:4)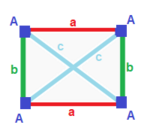

디지날 디스페노이드
(v:2+2; e:4+1+1; f:2+2)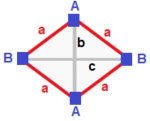

식물성 분산체
(v:2+2; e:2+2+1+1; f:2+2)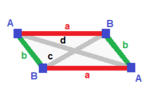

A 4 3 3---+-+-+++++++++++++++++++++++++++++++++++++++++++++

A 4 2 1 3 ----+---++++++-- 2 4 * 2 b 2 ---+++++++++++++++++++++++++++++++++++++++++++++++

A 4 1 1 1 3 ----+-+-+-+--- 2 2 * 2 b * 2 * 2 c * 2 * 2 * * 2 * * 2 ---+++-++-+--- abc 3 1 1 1 1 4

A 2 * 2 1 0 2 1 B * 2 0 1 1 2 --+ --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- aab 2 1 2 0 2 0 2 0 2 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2

A 2 * 1 0 1 1 2 B * 2 1 1 1 0 0 2 1 --+---------------------------------------------------------------------------------------------------------------------------------------------------------- 1 2 * 1 2 * 1 1 B 1 * 2 * 0 2 * * 0 2 * 0 -+-++++++++++ abcd 2 * abcd 2 * 2 * 2 * 2

삼각피라미드
(v:3+1, e:3+3; f:3+1)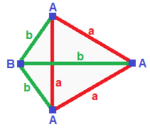

미러드 스피로이드
(v:2+1+1, e:2+2+1+1; f:2+1+1)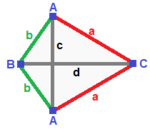

대칭 없음
(v:1+1+1+1; e:1+1+1+1+1+1; f:1+1+1+1)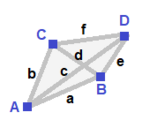

A 3 * 2 1 2 1 B * 1 0 3 3 0 ---++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

A  2 * *   1 1 0 1   1 1 1    B  * 1 *   2 0 1 0   0 2 1    C  * * 1   0 2 1 0   1 2 0  ---+-------+---------+------   a  1 0 1   2 * * *   0 1 1    b  0 1 1   * 2 * *   1 1 0    c  1 1 0   * * 1 *   0 2 0    d  0 0 2   * * * 1   1 0 1  ---+-------+---------+------ ABC  1 1 1   1 1 1 0   2 * * ACC  1 0 2   2 0 0 1   * 1 * BCC  0 1 2   0 2 0 1   ** 1

A   1 0 0 0   1 1 1 0 0 0   1 1 1 0   B   0 1 0 0   1 0 0 1 1 0   1 1 0 1   C   0 0 1 0   0 1 0 1 0 1   1 0 1 1   D   0 0 0 1   0 0 1 0 1 1   0 1 1 1 ----+---------+-------------+--------   a   1 1 0 0   1 0 0 0 0 0   1 1 0 0   b   1 0 1 0   0 1 0 0 0 0   1 0 1 0   c   1 0 0 1   0 0 1 0 0 0   0 1 1 0   d   0 1 1 0   0 0 0 1 0 0   1 0 0 1   e   01 0 1   0 0 0 0 1 0   0 1 0 1   f   0 0 1 1   0 0 0 0 0 1   0 0 1 1 ----+---------+-------------+-------- ABC   1 1 1 0   1 1 0 1 0 0   1 0 0 0 ABD   1 1 0 1   1 0 1 0 1 0   0 1 0 0 ACD   1 0 1 1   0 1 1 0 0 1   0 0 1 0 BCD   0 1 1 1   0 0 0 1 1 1   0 0 0 1

메모들

^ Klitzing, Richard. "Incidence Matrices".
^ Coxeter, 복합 일반 폴리토페스, 페이지 117
^ Lehrer & Taylor 2009, p.87
^ 복합 일반 폴리토페스, 페이지 117

참조

Coxeter, H.S.M. (1948), Regular Polytopes, Methuen and Co.
Coxeter, H.S.M. (1991), Regular Complex Polytopes, Cambridge University Press, ISBN 0-521-39490-2
Coxeter, H.S.M. (1999), "Self-dual configurations and regular graphs", The Beauty of Geometry, Dover, ISBN 0-486-40919-8

[1] Klitzing, Richard. "Incidence Matrices".

[2] Coxeter, 복합 일반 폴리토페스, 페이지 117

[3] Lehrer & Taylor 2009, p.87

[4] 복합 일반 폴리토페스, 페이지 117

[1]

[2]

[3]

[4]

Search