하세 다이어그램

순서 이론에서 하세 도표(/ˈhæsə/; 독일어: [ˈhasə])는 유한 부분 순서 집합을 나타내기 위해 사용되는 수학적 도표의 일종으로, 그 전이적 감소의 도면의 형태다. 구체적으로는 부분 순서의 집합(S, ≤)의 경우, 평면에서 S의 각 요소를 정점으로 나타내며, y가 x를 덮을 때마다(즉, x ≤ y와 x ≤ z가 없을 때마다) x에서 y로 위로 올라가는 선 세그먼트나 곡선을 그린다. 이러한 곡선은 서로 교차할 수 있지만 끝점 이외의 정점에 닿으면 안 된다. 이러한 다이어그램은 정점이 라벨로 표시되어 있으며, 그 순서가 부분적으로 결정된다.

이 도표는 헬무트 하세 (1898–1979)의 이름을 따서 명명되었다. 개럿 비르호프 (1948년)에 따르면, 이 도표들을 효과적으로 사용하기 때문에 그렇게 불린다. 그러나 하세가 이 도표를 처음 사용한 것은 아니었다. 하세보다 앞선 한 예는 앙리 구스타프 보그트(1895)에서 찾을 수 있다. 하세 다이어그램은 원래 부분적으로 순서가 정해진 세트를 손으로 그리기 위한 기법으로 고안되었지만, 최근에는 그래프 그리기 기법을 이용해 자동으로 만들어지고 있다.^[1]

"Hasse diagraphy"라는 문구는 또한 그 그래프의 어떤 도면과 독립적으로 추상적인 방향의 ACyclic graph로서 transitive 감소를 언급할 수 있지만, 이 용도는 여기에서 제외된다.^[2][3][4]

다이어그램 디자인

하세 다이어그램은 유한양행(poset)을 다루기 위한 직관적인 도구일 뿐 아니라 단순하지만, '좋은' 다이어그램은 그리기가 다소 어려운 것으로 나타났다. 그 이유는 일반적으로 주어진 포셋에 대해 Hasse 도표를 그리는 많은 가능한 방법이 있을 것이기 때문이다. 순서의 최소 요소부터 시작하여 점차적으로 더 큰 요소를 그리는 단순한 기법은 종종 꽤 좋지 않은 결과를 낳는다: 대칭과 내부 구조는 쉽게 상실된다.

다음의 예는 그 문제를 보여준다. 포함${\displaystyle }$ordered ${\displaystyle \subseteq }$에 의해 정렬된 4-element 세트의 전원 세트를 고려하십시오$.$ 다음은 이 부분 순서에 대한 4가지 Hasse 다이어그램입니다. 각 하위 집합에는 특정 요소가 하위 집합 (1)에 있는지 여부를 나타내는 이진 인코딩으로 표시된 노드가 있다.

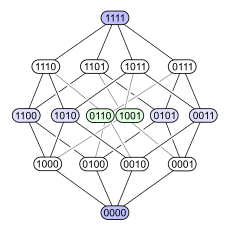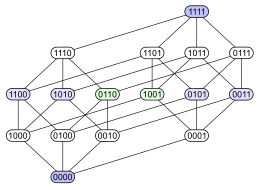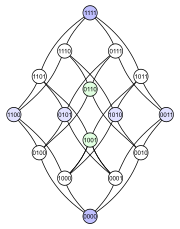첫 번째 도표를 보면 전원 세트가 등급이 매겨진 포셋임을 알 수 있다. 두 번째 도표는 같은 등급의 구조를 가지고 있지만, 다른 도표보다 일부 가장자리를 길게 하여 4차원 입방체는 두 개의 3차원 입방체의 결합체임을 강조하고 있으며, 4차원 입방체(추상 3-폴리토프) 역시 마찬가지로 두 개의 삼각형(추상 2-폴리토프)을 병합한다는 것을 강조한다. 세 번째 도표는 구조물의 내부 대칭의 일부를 보여준다. 네 번째 다이어그램에서 정점은 4×4 행렬의 요소처럼 배열되어 있다.

상향평형성

두 모서리가 교차하지 않는 Hasse 도표로 부분 순서를 그릴 수 있는 경우, 커버 그래프는 위쪽 평면이라고 한다. 상향 평면성 및 교차 없는 Hasse 다이어그램 구성에 대한 많은 결과가 알려져 있다.

• 부분 순서가 격자일 경우 최대 2개의 순서 차원이 있는 경우에만 교차 없이 그릴 수 있다.^[5] 이 경우 순서 차원을 실현하는 두 개의 선형 순서에서 원소의 위치로부터 원소에 대한 카르테시안 좌표를 도출한 다음 45도 각도로 도면을 시계 반대방향으로 회전시켜 비교차 도면을 찾을 수 있다.
• 부분 순서에 최소 요소가 하나 이상 있거나 최대 한 개의 최대 요소가 있는 경우, 교차하지 않는 Hasse 도표가 있는지 여부를 선형 시간 내에 시험할 수 있다.^[6]
• 다중 선원과 싱크가 있는 부분 순서를 교차 없는 Hasse 도표로 그릴 수 있는지 여부를 결정하는 것은 NP 완성이다.^[7] 그러나 교차 없는 Hasse 도표를 찾는 것은 부분 순서의 전이적 감소의 3차원 요소와 관절 지점의 수로 파라메트릭을 구했을 때 고정 매개변수를 추적할 수 있다.^[8]
• 부분 순서 요소의 y 좌표가 지정되면, 그러한 좌표 할당을 존중하는 교차 자유 하세 도표는 선형 시간 내에 찾을 수 있다.^[9] 특히 입력 포셋이 등급화된 포셋이라면 각 정점의 높이가 순위에 비례하는 교차 프리 하세 다이어그램이 있는지 선형적으로 판단할 수 있다.

UML 표기법

포함 체인의 표준 다이오라마는 상속 관계에 의해 세트를 연결하는 UML 등급이다. 그림에는 중첩된 집합 집합 집합 C:

B₁₃ = {♠, ♥, ♦, ♦}, B = {♠, ♥}, B₂ = {♦, ♣}, B = {♣};
C = {B₁, B, B₂, B₃}.

메모들

참조

• Baker, Kirby A.; Fishburn, Peter C.; Roberts, Fred S. (1971), "Partial orders of dimension 2", Networks, 2 (1): 11–28, doi:10.1002/net.3230020103.
• Bertolazzi, R; Di Battista, G.; Mannino, C.; Tamassia, R. (1993), "Optimal upward planarity testing of single-source digraphs" (PDF), Proc. 1st European Symposium on Algorithms (ESA '93), Lecture Notes in Computer Science, 726, Springer-Verlag, pp. 37–48, doi:10.1007/3-540-57273-2_42, ISBN 978-3-540-57273-2.
• Birkhoff, Garrett (1948), Lattice Theory (Revised ed.), American Mathematical Society.
• Chan, Hubert (2004), "A parameterized algorithm for upward planarity testing", Proc. 12th European Symposium on Algorithms (ESA '04), Lecture Notes in Computer Science, 3221, Springer-Verlag, pp. 157–168, doi:10.1007/978-3-540-30140-0_16.
• Di Battista, G.; Tamassia, R. (1988), "Algorithms for plane representation of acyclic digraphs", Theoretical Computer Science, 61 (2–3): 175–178, doi:10.1016/0304-3975(88)90123-5.
• Freese, Ralph (2004), "Automated lattice drawing", Concept Lattices, Lecture Notes in Computer Science, 2961, Springer-Verlag, pp. 589–590. 확장된 사전 인쇄를 온라인으로 이용할 수 있다. [1].
• Garg, Ashim; Tamassia, Roberto (1995a), "Upward planarity testing", Order, 12 (2): 109–133, doi:10.1007/BF01108622, S2CID 14183717.
• Garg, Ashim; Tamassia, Roberto (1995b), "On the computational complexity of upward and rectilinear planarity testing", Graph Drawing (Proc. GD '94), LectureNotes in Computer Science, 894, Springer-Verlag, pp. 286–297, doi:10.1007/3-540-58950-3_384, ISBN 978-3-540-58950-1.
• Jünger, Michael; Leipert, Sebastian (1999), "Level planar embedding in linear time", Graph Drawing (Proc. GD '99), Lecture Notes in Computer Science, 1731, pp. 72–81, doi:10.1007/3-540-46648-7_7, ISBN 978-3-540-66904-3.
• Vogt, Henri Gustav (1895), Leçons sur la résolution algébrique des équations, Nony, p. 91.

외부 링크

• Wikimedia Commons의 관련 미디어:
  • Hasse 다이어그램(갤러리)
  • Hasse 다이어그램(카테고리)
• Weisstein, Eric W. "Hasse Diagram". MathWorld.