편향(엔지니어링)

구조공학에서 편향이란 구조요소의 일부가 변형되기 때문에 하중에 의해 변위되는 정도를 말합니다.각도 또는 거리를 나타낼 수 있습니다.

하중을 받는 부재의 편향 거리는 하중을 받는 부재의 편향된 형상의 기울기를 수학적으로 기술하는 함수를 통합하여 계산할 수 있습니다.

개별 위치에서 일반적인 빔 구성과 로드 케이스를 편향하기 위한 표준 공식이 있습니다.그 외에는 가상작업, 직접적분, 카스틸리아노법, 맥컬레이법 또는 직접강성법 등의 방법을 사용한다.빔 요소의 편향은 보통 오일러-베르누이 빔 방정식을 기반으로 계산되는 반면 플레이트 또는 셸 요소의 편향은 플레이트 또는 셸 이론을 사용하여 계산됩니다.

이러한 맥락에서 편향의 사용의 예는 건물 건설에 있다.건축가와 엔지니어는 다양한 용도에 맞는 재료를 선택합니다.

다양한 하중 및 지지대에 대한 빔 편향

보의 형상 및 구성은 크게 다를 수 있습니다.예를 들어 빔은 직선 또는 곡선일 수 있습니다.단면이 일정하거나 가늘어질 수 있습니다.이는 완전히 동일한 재료(동종)로 구성될 수도 있고 다른 재료(복합)로 구성될 수도 있습니다.이러한 것들 중 일부는 분석을 어렵게 하지만, 많은 엔지니어링 응용 프로그램들은 그리 복잡하지 않은 사례들을 포함합니다.다음과 같은 경우 분석이 간소화됩니다.

• 빔은 원래 직선이고 테이퍼는 약간입니다.
• 빔은 선형 탄성 변형만 경험합니다.
• 빔이 가늘다(길이 대 높이 비율이 10보다 큼)
• 작은 편향만 고려된다(최대 편향은 스팬의 1/10 미만).

이 경우 빔의 편향($\displaystyle$ w$)$을 제어하는 방정식은 다음과 같이 근사할 수 있습니다.

${\displaystyle {\mathrm {d} ^{2}w(x)} {\mathrm {d} x^{2} = frac {M(x)} {E(x)I(x)}}$

여기서 $x$에 $대한{\displaystyle }$ 휘어진 모양의 두 번째 도함수$($$x는$$$빔의 길이를 따라 수평으로 위치)는 곡률로 해석되고, $(\displaystyle$$$E$)$는 영 계수,$I{\displaystyle }$(\$displaystyle$ I$)$는 단면 관성 모멘트, a.$nd{\displaystyle }$ M$(\displaystyle$ M$)$은 빔의 내부 벤딩 모멘트입니다.

또한 빔이 테이퍼되지 않고 균질하며 분산 $부하{\displaystyle }$q\$display$q$\backslash$$style$ q에 의해 작용되는 경우 위의 식은 다음과 같이 쓸 수 있습니다.

${\displaystyle EI~{\cfrac {d}^{4}w(x)}{\mathrm {d} x^{4}}=q(x)}$

이 방정식은 다양한 하중 및 경계 조건에 대해 풀 수 있습니다.몇 가지 간단한 예를 다음에 제시하겠습니다.표현식은 길고 가늘고 균일한 프리즘 빔과 작은 굴절 및 선형 탄성 특성을 위해 개발된 근사치입니다.이러한 제한 하에서 근사치는 실제 편향의 5% 이내에서 결과를 제공해야 한다.

캔틸레버 보

캔틸레버 보에는 한쪽 끝이 고정되므로 해당 끝의 기울기와 처짐은 0이어야 합니다.

엔드 로드 캔틸레버 보

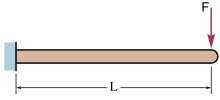
예제 이미지에서 자유단에서의 탄성 편향$\delta {\displaystyle }$ {$displaystyle \delta}$및 편향 각도 $\delta {\displaystyle }$ ${displaystyle \phi$}($$라디안 단위)는 다음과 같이 ^[1]계산할 수 있습니다. 끝 부하가 있는 A(무중력) 캔틸레버 빔은 자유단 B에서 계산됩니다.

${\displaystyle_{B}=flac{FL^{3}}}{3EI}}}$

${\displaystyle\phi_{B}=blac {FL^{2}}{2EI}}}$

어디에

${\displaystyle F}${\$displaystyle$ F$}$ =$$ 빔 선단에 작용하는 힘

${\displaystyle L}${\$displaystyle$L} =$$ 빔 길이(스팬)

${\displaystyle E}${\$displaystyle$E} =$$ 탄성 계수

${\displaystyle I}$\ $displaystyle$ I$$=$$ 빔 단면의 관성 모멘트

스팬이 2배로 늘어나면 편향은 8배로 증가합니다.엔드 로드 캔틸레버 빔의 스팬에 따른 임의의 지점$x{\displaystyle }$ {\$style$ x$\}$에서의 편향은 다음을 ^[1]사용하여 계산할 수 있습니다.

${\displaystyle_{x}=black{Fx^{2}}{6}EI}}(3L-x)}$

${\displaystyle\phi_{x}=black{Fx}{2EI}}(2L-x)}$

주의: x ${\displaystyle =}$ {$displaystyle$ x$=L}$ (빔의 끝)에서 ${\displaystyle x_{}}$x x x \$displaystyle _{x}$ 및$$ ${\displaystyle x_{}}$x \$display$ style $\phi$_{$x}$ 방정식은$$ 위의 ${\displaystyle b_{}}$ B$$\$displaystyle$\$phi$ _${B}$ 및$$$$ ${\displaystyle {\varphi }_{}}$B \$displaystyle \pi$ _${B}$

균일 하중 캔틸레버 보

균일한 하중을 받는 캔틸레버 빔의 자유단 B에서의 편향은 다음과 같습니다.^[1]

${\displaystyle_{B}=blac{qL^{4}}{8}EI}}}$

${\displaystyle\phi_{B}=blac{qL^{3}}{6EI}}}$

어디에

${\displaystyle q}${$displaystyle$q} =$$ 빔의 균일한 하중(단위 길이당 힘)

${\displaystyle L}${\$displaystyle$L} =$$ 빔 길이

${\displaystyle E}${\$displaystyle$E} =$$ 탄성 계수

$\displaystyle$ I$$=$$ 단면 관성 모멘트

균일하게 부하가 가해진 캔틸레버 빔의 스팬에 따른 임의의 점$x{\displaystyle }$ {\$style$ x$\}$에서의 편향은 다음을 ^[1]사용하여 계산할 수 있습니다.

${\displaystyle_{x}=black{qx^{2}}{24EI}}(6L^{2}-4Lx+x^{2})}$

${\displaystyle\phi_{x}=black{qx}{6EI}}(3L^{2}-3Lx+x^{2})}$

단순 지지 보

단순하게 지지된 보의 끝 부분에는 회전이 가능하지만 휘어지지 않는 지지대가 있습니다.

중앙부하형 단순보

단순히 지지된 빔이 로드된 중앙의 스팬을 따라 x$\style$ x$\}$의 임의의 지점에서의 편향은 다음을 ^[1]사용하여 계산할 수 있습니다.

${\displaystyle \display_{x}=syslogfrac {Fx}{48EI}}(3L^{2}-4x^{2})}$

위해서

$\displaystyle 0\leq x\leq\frac {L}{2}}$

두 개의 간단한 지지대에 의해 지지되고 중심에 하중을 가하는 빔의 중간점 C에서의 탄성 편향의 특수한 경우는 다음과 ^[1]같이 주어진다.

${\displaystyle_{C}=flac{FL^{3}}{48}EI}}}$

어디에

${\displaystyle F}${\$displaystyle$ F$}$ =$$ 빔의 중심에 작용하는 힘

${\displaystyle L}${\$displaystyle$ L$}$ =$$ 지지대 사이의 빔 길이

${\displaystyle E}${\$displaystyle$E} =$$ 탄성 계수

$\displaystyle$ I$$=$$ 단면 관성 모멘트

중심에서 벗어난 단순 빔

가장 가까운 지지대로부터 \$displaystyle$ a$}$ 거리에$$ $있는{\displaystyle }$ 두 개의 단순 지지대로 지지된 빔의 최대 탄성 편향은 다음과 같습니다.^[1]

${\displaystyle _{max}=sqrt {Fa(L^{2}-a^{2})^{3/2}}{9{\sqrt {3}}LEI}}}$

어디에

${\displaystyle F}${\$displaystyle$ F$}$ =$$ 빔에 작용하는 힘

${\displaystyle L}${\$displaystyle$ L$}$ =$$ 지지대 사이의 빔 길이

${\displaystyle E}${\$displaystyle$E} =$$ 탄성 계수

${\displaystyle I}$ ${displaystyle$ I$}$ =$$ 단면 관성 모멘트

${\displaystyle \mathrm{하중}}$에서 가장 가까운 지지대까지의 거리$(\displaystyle$ a$)$ =$$

이 최대 편향은 가장 가까운 지지대로부터 x $(\$ x_${1})$ $거리$에서 발생하며 다음과 같이 ^[1]구합니다.

$({displaystyle x_{1}={frac {L^{2}-a^{2}}}:{3}}})$

균일 하중 단순 보

(그림과 같이) 균일한 하중 하에서 두 개의 단순 지지대에 의해 지지된 빔의 탄성 편향(중간점 C)은 다음과 같다.^[1]

${\displaystyle_{C}=blac{5qL^{4}}{384EI}}}$

어디에

${\displaystyle q}${$displaystyle$q} =$$ 빔의 균일한 하중(단위 길이당 힘)

${\displaystyle L}${\$displaystyle$L} =$$ 빔 길이

${\displaystyle E}${\$displaystyle$E} =$$ 탄성 계수

$\displaystyle$ I$$=$$ 단면 관성 모멘트

균일하게 로드된 단순 지지 빔의 스팬에 따른 x$${\$style$x$\}$의 편향은 다음을 ^[1]사용하여 계산할 수 있습니다.

${\displaystyle \displaystyle _{x}=syslogfrac {qx}{24EI}}(L^{3}-2Lx^{2}+x^{3})}$

길이 변경

빔의 $길이{\displaystyle \mathrm{}}$ ${\displaystyle \delta }$ L$(\displaystyle$ \$Delta$L$$)의 변화는 구조에서는 일반적으로 무시할 수 있지만 편향 함수 ${\displaystyle {\delta }_{}}$x {\$displaystyle \theta$ _${$x$$$$$}}$가 모든$$x {\$displaystyle$ x$\}$에 대해 알려진 경우 기울기 ${\displaystyle {\delta }_{}}$x {\$displaystyle \$$theta$ _${x$} 함수를 통합하여 계산할 수 있습니다.

장소:

$L$ \$displaystyle$ \ $Delta$L $$= 길이 변화(항상 음수)

$x$ \$displaystyle$ \ $theta _${ x }$$ = 기울기 함수 ( ${\$ $x$ \$displaystyle$ \ displaystyle $_${$$x }의 첫 번째 ${\displaystyle {\mathrm{도함수}}_{}}$)

$\displaystyle \Delta L=-{\frac {1}{2}}\int _{0}^{L}(\theta(x))^{2}개요}$ ^[2]

빔이 균일하고 어떤 점에서의 편향이 알려진 경우 빔의 다른 특성을 몰라도 이를 계산할 수 있습니다.

단위

위에 제공된 공식에서는 일관된 단위 집합을 사용해야 합니다.대부분의 계산은 SI(International System of Units) 또는 미국 관습 단위로 이루어지지만, 다른 많은 단위 시스템이 있다.

국제 시스템(SI)

힘: 뉴턴 ($\style$ N$)$

길이: 미터 ($\displaystyle$ m$)$

탄성계수: ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{m2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}P}$a$$) { $displaystyle${ $frac${ $N$} { $m^$ {2$}$ } ($Pa )$

관성모멘트: ${\displaystyle {m4\mathrm{}}^{}}${ $displaystyle m^$ { 4$$}

미국 관습 단위(US)

힘: 무게 (${\displaystyle }$ ${\displaystyle b_{}}$ f$${$display$ style $lb_{f$

길이: ${\displaystyle \mathrm{인치}}$ $(\displaystyle$ in$)$

탄성계수: ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{b_{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ n$$ ({$displaystyle {lb_{f}}{in^{2}}})$

관성 모멘트: ${\displaystyle {in\mathrm{}}^{}}$4 { $style$ in ^ { 4$$}

다른이들

다른 유닛도 사용할 수 있습니다.단, 자기 정합성이 있는 경우입니다.$$를 들어, ${\displaystyle {}_{}}$ 힘( ${\displaystyle k_{}}$g f { $displaystyle$kg _ {$$f $\}$ ) 단위가 부하 측정에 사용되는 경우가 있습니다.이 경우 탄성계수는 k ${\displaystyle \frac{g_{}}{}}$ f $({$로 환산하여야 한다.

구조 편향

건물 코드는 최대 굴곡을 결정합니다(일반적으로 1/400 또는 1/600과 같은 스팬의 일부).강도 제한 상태(허용 응력) 또는 사용 가능성 제한 상태(편향 고려 사항 등)가 필요한 부재의 최소 치수를 좌우할 수 있다.

구조물의 목적을 위해 처짐을 고려해야 한다.유리 패널을 고정하는 강철 프레임을 설계할 때 유리의 파열을 방지하기 위해 최소한의 편향만 허용합니다.

빔의 편향된 모양은 모멘트 다이어그램으로 나타낼 수 있습니다(지지 조건을 적용하기 위해 두 번, 회전 및 변환).

참고 항목

• 경사 편향법

레퍼런스

외부 링크

• 보의 편향
• 빔 편향
• 보의 처짐 및 기울기를 위한 계산 도구