직접강성법

구조해석 방법의 하나로, 매트릭스 강성법이라고도 하는 직접강성법은 정적으로 불확실한 유형을 포함한 복잡한 구조물의 컴퓨터 자동화 분석에 특히 적합하다. 구조물의 부재력 계산 및 변위 시 구성원의 강성 관계를 이용하는 매트릭스 방식이다. 직접강성법은 유한요소법(FEM)의 가장 보편적인 구현이다. 이 방법을 적용할 때 시스템은 노드에 상호 연결된 단순하고 이상적인 요소 집합으로 모델링되어야 한다. 이 요소들의 재료 강성 특성은 매트릭스 수학을 통해 전체 이상 구조물의 거동을 지배하는 단일 매트릭스 방정식으로 정리된다. 그 구조의 알려지지 않은 변위와 힘은 이 방정식을 풀어서 결정할 수 있다. 직접강성법은 대부분의 상용 및 자유원소 유한요소 소프트웨어의 기초를 형성한다.

직접강성법은 항공우주 분야에서 비롯되었다. 연구원들은 복잡한 비행기 프레임의 분석을 위한 다양한 접근법을 살펴보았다. 여기에는 탄성 이론, 구조 역학의 에너지 원리, 유연성 방법 및 매트릭스 강성 방법이 포함되었다. 직접강성법이 컴퓨터 구현에 이상적으로 적합한 효율적인 방법으로 등장한 것은 이러한 방법들의 분석을 통해서였다.

역사

1934년과 1938년 사이에 A. R. Collar와 W. J. Duncan은 오늘날 사용되는 매트릭스 시스템의 표현과 용어가 있는 최초의 논문을 발표했다. 공기탄성 연구는 제2차 세계대전을 통해 계속되었지만 1938년부터 1947년까지의 출판 제한으로 인해 이 작품의 추적이 어려워졌다. 매트릭스 구조 해석의 두 번째 큰 돌파구는 1954년과 1955년 존 H 교수 때 일어났다. Argyris는 구조물의 요소 요소들을 방정식 체계로 조립하는 개념을 체계화했다. 마지막으로 1959년 11월 6일, 보잉의 Structural Dynamics Unit의 대표 M. J. Turner는 컴퓨터 구현을 위한 효율적인 모델로서의 직접 강성 방법을 개괄적으로 설명하는 논문을 발표했다(Felippa 2001).

회원강성관계

일반적인 부재 강성 관계는 다음과 같은 일반적인 형태를 가진다.

${\displaystyle \mathbf {Q} ^{m}=\mathbf {k} ^{m}\mathbf {q} ^{m}+\mathbf {Q} ^{om}}}}}$

(1)

어디에

m = 멤버 번호 m.

${\displaystyle {\mathbf{Q}}^{}}$ ${\displaystyle {}^{}}$ ${\$ $$= 알 수 없는 내부 힘인 부재 특성력의 벡터.

${\displaystyle {\mathbf{k}}^{}}$ ${\displaystyle {}^{}}$ ${\$ $$= 변형에 대한 부재의 저항성을 특징짓는 부재 강성 행렬.

${\displaystyle {\mathbf{q}}^{}}$ ${\displaystyle {}^{}}$ ${\$ $$= 부재 특성 변위 또는 변형의 벡터.

${\displaystyle {\mathbf{Q}}^{}}$ ${\displaystyle o^{}}$ m ${\$ = 외부 효과(예: 알려진 힘 및 온도 변화)로 인해 발생하는 멤버 특성 힘의 벡터인 반면 ${\displaystyle {}^{}}$= ${\displaystyle 0}$ ${\displaystyle \mathbf {q} ^{m}=0$ .

${\displaystyle {}^{}}$ ${\$이(가) 절대 변위가 아닌 멤버 변형이라면$$ ${\displaystyle {}^{}}$ ${\$은 독립 멤버 힘이며$$, 이 경우 (1)을 반전시켜 유연성 방법에 사용되는 소위 멤버 유연성 매트릭스를 산출할 수 있다.

시스템 강성 관계

노드라고 하는 지점에서 많은 멤버가 상호 연결된 시스템의 경우, Eq.(1)와 같은 멤버의 강성 관계는 다음과 같은 관찰을 활용하여 통합할 수 있다.

• 멤버 변형 ${\displaystyle {}^{}}$ ${\$은(는) 멤버 간 호환성을 보장하기 위해 시스템 노달 변위 r 단위로 표현할 수 있다$$. 이는 r이 일차 미지의 대상이 될 것임을 암시한다.
• 멤버 힘 ${\displaystyle {}^{}}$ ${\$은(는) 노드가 노드의 평형을 유지하는 데 도움을 준다. 이는 (1)의 우측이 전체 시스템에 대해 다음과 같은 노달 평형 방정식의 우측에 통합된다는 것을 의미한다.

${\displaystyle \mathbf {R} =\mathbf {Kr} +\mathbf {R} ^{o}}}$

(2)

어디에

${\displaystyle \mathbf{R}}$ ${\$ $$$}$ = 시스템 노드에 가해지는 외부 힘을 나타내는 노드 힘의 벡터.

${\displaystyle \mathbf{K}}$ ${\$ $$= 시스템 강성 매트릭스 $k{\displaystyle {\mathbf{}}^{}}$ ${\$을(를) 조립하여 설정한다$.$

${\displaystyle \mathbf{r}}$ ${\$ $$$}$ = 임의의 노드 힘 R에 따라 시스템의 가능한 모든 변형 구성을 정의할 수 있는 시스템 노드 변위 벡터.

${\displaystyle {\mathbf{R}}^{}}$ ${\displaystyle {}^{}}$ ${\$ $$= 앞의 결절력 벡터 R에 이미 포함된 결절력을 제외한 모든 외부 효과를 나타내는 등가 결절력의 벡터. 이 벡터는 $구성원$의 Q ${\displaystyle o^{}}$ m ${\$^{$om$을(를) 조립하여 설정한다.

해결책

벡터 R과 r의 크기가 같기 때문에 시스템 강성 매트릭스 K는 정사각형이다. 또한 $k{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}$ ${\$이(가) 대칭이기 때문에 대칭이다. 서포트의 제약조건을 (2)에서 설명하면, 다음과 같은 상징적으로 선형 방정식 시스템(2)을 풀어서 결절 변위를 발견한다.

${\displaystyle \mathbf {r} =\mathbf {K} ^{1}(\mathbf {R} -\mathbf {R} ^{o})\qquad \qquad \qquad \qquad \mathrmet{(3)}}}}}}}}}$

이후 호환성을 고려하여 q.(1)에서 $q{\displaystyle {\mathbf{}}^{}}$ m ${\$을(를) 찾을 수$$ 있다.

직접강성법

$.($1)를 ${\displaystyle {}^{}}$ m {\displaystyle$\mathbf$ {$q}{m$}}과$($$와{\displaystyle {\mathbf{}}^{}}$) o m ${\$이(가) 각각 r 및 R과 방향에서 일치하는 멤버 엔드 변위 및 힘인 형태로 갖는 것이 일반적이다. 이$$ 경우 $K{\displaystyle \mathbf{}}$ ${\$및$$ $R{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}$ ${\$${\displaystyle {}^{}}$${R} ^{o}}$을(를) 구성원의 행렬 $k{\displaystyle {\mathbf{}}^{}}$ ${\$ $\$$mathbf$ {$k} ^{m$$}$ $및$ Q ${\displaystyle {\mathrm{om}}^{}}$ ${\$$\matbf.$ 이 방법은 직강성법으로 알려져 있다.

매트릭스 강성법의 장단점을 비교하고 유연성 방법 기사에서 논의한다.

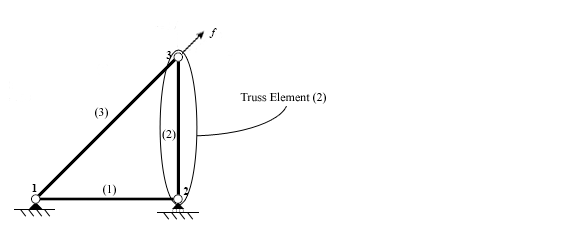
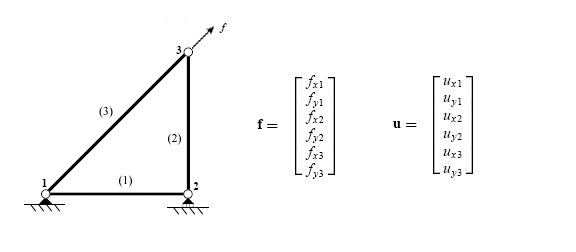
예

고장

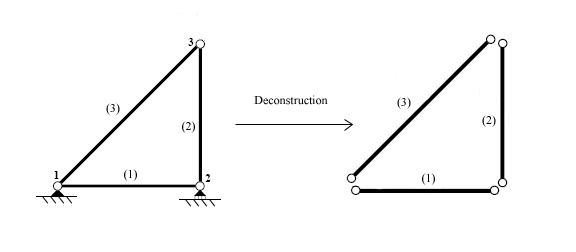
직접강성법을 사용할 때 첫 번째 단계는 구조물을 구성하는 개별 요소를 식별하는 것이다.

요소들이 식별되면, 구조물은 다른 요소들을 서로 연결하는 지점인 노드에서 분리된다.

그런 다음 각 원소를 개별적으로 분석하여 부재 강성 방정식을 개발한다. 힘과 변위는 원소의 기하학적 구조와 특성에 따라 달라지는 요소 강성 행렬을 통해 연관된다.

트러스 요소는 압축이나 장력에서만 힘을 전달할 수 있다. 즉, 2차원에서는 각 노드의 자유도(DOF: 수평 및 수직 변위)가 2개임을 의미한다. 결과 방정식은 4 X 4 강성 행렬을 포함한다.

${\displaystyle {\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}}$

프레임 요소는 압축과 장력 외에도 벤딩 모멘트를 견딜 수 있다. 이는 수평 변위, 수직 변위 및 평면 내 회전 등 3개의 자유도를 초래한다. 이 경우의 강성 행렬은 6 X 6이다.

${\displaystyle{\begin{bmatrix}f_{x1}\\f_{y1}\\m_{z1}\\f_{미국}\\f_{y2}\\m_{z2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&, k_{12}&, k_{13}&, k_{14}&, k_{15}&, k_{16}\\k_{21}&, k_{22}&, k_{23}&, k_{24}&, k_{25}&, k_{26}\\k_{31일}&, k_{32}&, k_{33}&, k_{34}&, k_{35}&, k_{36}\\k_{41}&, k_{42}&, k_{43}&, k_{44}&, k_{45}&앰프, k_{46}\\k_{51}&, k_{52}&, k_{53}&, k_{54}&, k_{55}&, k_{56}\\k_{61}&, k_{62}&, k_{63}&, k_{64}&k_{65}&k_{66}\\\end{bmatrix}}{{bmatrix}u_{x1}\\u_{y1}\\\theta _{z1}\{x2}\u_{y2}\nd{bmatrix}}}}}}}{bmatrix}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

판과 쉘과 같은 다른 요소들도 직접 강성 방법에 통합될 수 있으며 유사한 방정식을 개발해야 한다.

조립

개별 요소 강성 관계가 개발되면 원래 구조로 조립되어야 한다. 이 과정의 첫 단계는 개별 요소에 대한 강성 관계를 전체 구조에 대한 글로벌 시스템으로 전환하는 것이다. 트러스 요소의 경우 강성법의 글로벌 형태는 글로벌 좌표계에 관한 요소의 각도에 따라 달라진다(이 시스템은 일반적으로 전통적인 데카르트 좌표계다).

${\displaystyle {\begin{bmatrix}f_{x1}\f_{y1}\f_{x2}\f_{y2}\\end{bmatrix}}={\frac {EA}{{$$EA}{}}}}}{x}}\f_{x2}\f_}}}}}{$L}}{\begin{bmatrix}c^{2}&, sc&, -c^{2}&, -sc\\sc&, s^{2}&, -sc&, -s^{2}\\-c^{2}&, -sc&, c^{2}&, sc\\-sc&, -s^{2}&, sc&, s^{2}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{미국}\\u_{y2}\\\end{bmatrix}}{\begin{배열}{r}s=\sin\beta \\c=\cos(\\\end{배열}}}(각도에서 트러스 요소 β에)Equivalently, -LSB-. f=1f:1f)2fYUx1너는 y1ux2너는 y2]{\displaystyle{\begin{bmatrix}f_{x1}\\f_{y1}\\\hline f_{미국}\\f_{y2}\end{bmatrix}}={\frac{EA}{L}}\left는 경우에는{\begin{배열}{cccc}c_{)}c_{)}&, c_{)}c_{y}&, -c_{)}c_{)}&, -c_{)}c_{y}\\c_{y}c_{)}&, c_{y}c_{y}&, -c_{y}c_{)}&, -c_{y}c_{y}\\\hline -c_{)}c_{)}&, -c_{)}c_{y}&, c_{)}c._{)}&, c_{)}c_{y}\\-c_{y}c_{)$}}&-c_{y}c_{y}c_{x}&c_{x}&c_{x}\\end{array}\right]{\bmatrix}u_{x1}\u_\hline u_{x2}\u_{bmatrix}}}}}}}}}}$

여기서 $c{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ 및$$ $c{\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\$는 트러스 요소의 방향 코사인(즉, 구성원과 정렬된 단위 벡터의 구성 요소)이다$$. 이 형태는 이 제형에 뚜렷이 나타나는 패턴을 단순히 확장함으로써 요소 강성을 3-D 공간 트러스로 일반화하는 방법을 보여준다.

글로벌 좌표계에서 요소 강성 행렬을 개발한 후에는 반드시 단일 "마스터" 또는 "글로벌" 강성 행렬로 병합해야 한다. 이러한 행렬을 함께 병합할 때 반드시 따라야 할 두 가지 규칙이 있다. 즉, 각 노드의 변위 호환성 및 힘 평형이다. 이러한 규칙은 요소 노달 변위와 전역 노달 변위를 연관시킴으로써 유지된다.

전역 변위와 힘 벡터는 각각 구조물의 각 자유도에 대해 하나의 입력을 포함한다. 소자 강성 행렬은 전역 변위 및 하중 벡터에 따라 각 행렬을 증가시키거나 확장하여 병합된다.

${\displaystyle k^{(1)={\frac {EA}{L}{{}{\begin{bmatrix}1&0&0\\0&0&0&0\\\-1&0&0\\\0&0&0\\\end{bmatrix}}\오른쪽 화살표 K^{(1)={\frac {EA}{\frac {EA}{}}}{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}L}{{{\begin{bmatrix}1&0&0&0&0&0&0\\0&0&0&0&0&0\\1&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0\endmatrix}}}}}}}\{bmatrix}}}$ (위 구조물의 요소 (1)에 대하여)

마지막으로, 글로벌 강성 매트릭스는 확장된 개별 요소 매트릭스를 함께 추가함으로써 구성된다.

해결책

일단 전지구 강성 행렬, 변위 벡터, 힘 벡터가 구성되면, 시스템은 단일 행렬 방정식으로 표현될 수 있다.

구조물의 각 자유도에 대해 변위 또는 힘이 알려져 있다.

각 자유도에 대해 알려진 값을 삽입한 후 마스터 강성 방정식을 완성하고 평가할 준비가 된다. 매트릭스 방정식을 평가하는 데 사용할 수 있는 몇 가지 다른 방법이 있는데, 여기에는 슐레스키 분해 및 방정식 시스템의 짐승력 평가가 포함된다. 구조물이 적절하게 구속되지 않은 경우, 힘을 가하면 구조물이 단단하게 이동하게 되고 추가 지지 조건이 추가되어야 한다.

이 절에서 설명하는 방법은 직접강성법의 개요를 의미한다. 공정에 대한 자세한 내용은 물론 공정에 내재된 재료 특성에 대한 가정을 위해 추가 출처를 참조해야 한다.

적용들

직접강성법은 컴퓨터 소프트웨어로 효율적이고 쉽게 구현해 다수의 요소가 포함된 복잡한 구조를 평가하기 위해 특별히 개발됐다. 오늘날, 이용 가능한 거의 모든 유한요소해결기는 직접강성법에 기초한다. 각 프로그램은 동일한 프로세스를 활용하지만, 많은 프로그램들이 연산 시간을 줄이고 필요한 메모리를 줄이기 위해 능률화되었다. 이를 위해 지름길이 개발됐다.

직접강성법을 활용하는 가장 큰 영역 중 하나는 이 방법이 모델링 소프트웨어에 통합된 구조해석 분야다. 소프트웨어는 사용자가 구조를 모델링할 수 있도록 하며, 사용자가 요소의 재료 특성을 정의한 후 프로그램은 자동으로 요소와 글로벌 강성 관계를 생성한다. 다양한 하중 조건이 적용될 때 소프트웨어는 구조를 평가하고 사용자에 대한 편향을 생성한다.

참고 항목

• 유한요소법
• 구조역학에서의 유한요소법
• 구조해석
• 융통성
• 유한요소 소프트웨어 패키지 목록

외부 링크

• 1-D 스프링 시스템에 대한 직접강성법의 적용
• 매트릭스 구조 해석
• 강성해석 시뮬레이션 애니메이션

참조

• Felippa, Carlos A. (2001), "A historical outline of matrix structural analysis: a play in three acts" (PDF), Computers & Structures, 79 (14): 1313–1324, doi:10.1016/S0045-7949(01)00025-6, ISSN 0045-7949, archived from the original (PDF) on 2007-06-29, retrieved 2005-10-05
• 펠리파, 카를로스 A. 유한요소법의 도입. 2001년 가을. 콜로라도 대학교 2005년 9월 18일
• 로빈슨, 존. 엔지니어를 위한 구조 매트릭스 분석. 뉴욕: John Wiley & Sons, 1966년
• 루빈스타인, 모셰 F. 구조물의 매트릭스 컴퓨터 분석. 뉴저지 주: 프렌티스 홀, 1966년
• 맥과이어, W, 갤러거, R. H, 지미안, R. D. 매트릭스 구조 분석, 2차 에드. 뉴욕: John Wiley & Sons, 2000년.