이중 객체

수학의 한 분야인 범주 이론에서, 이중 물체는 임의의 단일 범주에서 물체에 대한 선형 대수로부터 이중 벡터 공간을 아날로그로 나타낸 것이다.유한차원 벡터 공간에 대한 이중성의 범주형 특성에 기초하여 부분 일반화에 불과하다.이중성을 인정하는 물체를 이중화 가능한 물체라고 한다.이 형식주의에서는 이중 벡터 공간 V가 공리를 만족시키지 못하기^∗ 때문에 무한 차원 벡터 공간은 이원화할 수 없다.^[1]종종 어떤 물체는 그것이 어떤 미세성이나 콤팩트한 특성을 만족시킬 때만 이중화될 수 있다.^[2]

각 물체가 이중성을 갖는 범주를 자율 또는 강체라고 한다.표준 텐서 곱을 가진 유한차원 벡터 공간의 범주는 경직된 반면, 모든 벡터 공간의 범주는 그렇지 않다.

동기

V를 어떤 필드 K 위에 있는 유한차원 벡터 공간이 되게 하라.이중 벡터 공간 V의^∗ 표준 개념은 다음과 같은 특성을 가지고 있다: 모든 K-벡터 공간 U와 W에 대해 Hom_K(U ⊗ V,W) = Hom_K(U, V^∗ ⊗ W)이 있으며, 이는 V를^∗ 고유한 이형성에까지 특성화한다.이 표현은 벡터 공간의 텐서 곱을 적절하게 대체한 어떤 범주에서도 타당하다.모든 단일 범주(C, ⊗)의 경우, 2차 범주의 자연 이형성을 갖는 개체 V^∗ ∈ C로 개체 V의 이중 정의를 시도할 수 있다.

홈_C_C(–)₁ ⊗ V, (–)₂ → 홈(–),₁ V^∗ ⊗ (–)₂

이중성에 대한 올바른 행동 개념을 위해서는 이 지도가 범주 이론의 의미에서 자연적일 뿐만 아니라 어떤 면에서는 단조로운 구조를 존중해야 한다.^[1]따라서 이중 물체의 실제 정의는 더 복잡하다.

닫힌 단면체 범주 C, 즉 내부 Hom functor가 있는 단면체 범주에서 대체 접근법은 이중 벡터 공간의 표준 정의를 함수 공간으로서 시뮬레이션하는 것이다.V ∈ C는 V를^∗ ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ C ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ ( ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ $){\displaystyle {\underline {\mathrm {Hom}}}}{C}(V,\mathb {$ 1 $} _{C})$ 로 정의하며 ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ 여기서 1은_C 단일 ID다.경우에 따라서는 이 물체가 위의 의미에서는 V의 이중적인 물체가 되겠지만, 일반적으로는 다른 이론으로 이어진다.^[3]

정의

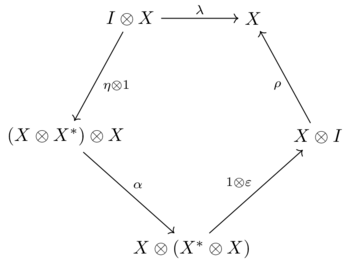
단일 범주 $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ , $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ , $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ , $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ , $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ , $λ$ )에 있는 $X$ $개체$ X ${\displaystyle$ $X}$ 을(를 $)$ 고려하십시오 $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ $X^{*}$ X ${{\$ X $^{*}}$ 는 $X^{*}$ 두 가지 형태론이 있는 경우 $X$ $X$ $X$ 의 왼쪽 이중이라고 한다.

{\

I\to

X

\otimes X^{*}}

은

\eta :I\to X\otimes X^{*}

는) 공동평가로,

\varepsilon :X^{*}\otimes X\to I

:

\varepsilon :X^{*}\otimes X\to I

\varepsilon :X^{*}\otimes X\to I

X

\varepsilon :X^{*}\otimes X\to I

→

\varepsilon :X^{*}\otimes X\to I

{\displaystyle \varepsilon

:

X^{*}\otimes

X

\to

I}은

(

는

\varepsilon :X^{*}\otimes X\to I

평가로 불렀다.

다음과 같은 두 개의 도표가 통근하도록 한다.

그리고

$X$ ${\displaystyle$ X $}$ 라는 $X^{*}$ 는 X $X^{*}$ {\ $displaystyle$ X $^{*}}$ 의 오른쪽 이중으로 불린다 $X$ $X^{*}$ 이 정의는 돌드와 인형에 기인한다.

왼쪽 듀얼은 오른쪽 듀얼과 마찬가지로 표준적으로 이형성이 있다.C가 땋은 경우(또는 대칭) 모든 왼쪽 이중도 역시 오른쪽 이중이며, 그 반대도 마찬가지다.

만약 우리가 단일 범주를 하나의 물체를 가진 2종류로 간주한다면, 이중 쌍은 정확히 부선 쌍이다.

예

표준 텐서 제품을 사용하는 필드 K에 대한 벡터 공간의 단일 범주(Vector_K, ⊗)_K를 고려한다.공간 V는 유한한 차원일 경우에만 이중화할 수 있으며, 이 경우 이중 객체 V는^∗ 이중 벡터 공간의 표준 개념과 일치한다.
표준 텐서 제품과 함께 정류 링 R을 통해 모듈의 단일 범주(Mod_R, ⊗)_R를 고려한다.모듈 M은 정밀하게 생성된 투영 모듈인 경우에만 이중화할 수 있다.이 경우 이중 물체^∗ M은 동형체 Hom_R(M, R)의 모듈에 의해서도 주어진다.
단일체 구조로 스매시 제품이 있는 뾰족한 스펙트럼 Ho(Sp)의 호모토피 범주를 고려한다.M이 $\mathbb {R} ^{n}$ ${\$ ^{ $n}}$ 의 콤팩트한 근린 수축장치인 경우(예: 콤팩트한 부드러운 다지관) 해당 포인트 스펙트럼^∞ ((M⁺)은 이중화 가능하다.이는 스페니어의 결과물이다.화이트헤드 이중성, 컴팩트 매니폴드의 경우 특히 푸앵카레 이중성을 암시한다.^[1]
$\mathrm {End} (\mathbf {C} )$ $\mathbf {C}$ ${\$ $daystyle \mathrm {End}(\mathbf {C$ $})$ 범주 $\mathrm {End} (\mathbf {C} )$ $\mathrm {End} (\mathbf {C} )$ {\ $displaystyle \mathbf {C}$ 는 펑커 구성의 단일 범주다 $\mathbf {C}$ .Functor $F$ $F$ 은 $F$ (는 $G$ ) $F$ $F$ 을(를) G $G$ 에 연결한 경우에만 Functor $G$ $G$ 의 왼쪽 이중이다 $F$ $G$ ^[4]

듀얼이 있는 범주

모든 물체가 왼쪽(우측) 이중(우측)을 갖는 단면형 범주를 왼쪽(우측) 자율 범주라고 부르기도 한다.대수 기하학자들은 이를 좌(우) 경직된 범주라고 부른다.모든 물체가 왼쪽과 오른쪽 이중 모두를 갖는 단면체 범주를 자율 범주라고 한다.또한 대칭인 자율 범주를 콤팩트 클로즈드 범주라고 한다.

트레이스

이중화할 수 있는 물체의 어떤 내형성 f는 추적을 인정하는데, 이것은 C의 단형 단위의 어떤 내형성이다.이 개념은 매우 특별한 경우로서, 선형 대수에서의 추적과 체인 콤플렉스의 오일러 특성을 포함한다.

참고 항목

이원화 객체

참조

^ ^a ^b ^c Ponto, Kate; Shulman, Michael (2014). "Traces in symmetric monoidal categories". Expositiones Mathematicae. 32 (3): 248–273. arXiv:1107.6032. Bibcode:2011arXiv1107.6032P.
^ Becker, James C.; Gottlieb, Daniel Henry (1999). "A history of duality in algebraic topology" (PDF). In James, I.M. (ed.). History of topology. North Holland. pp. 725–745. ISBN 9780444823755.
^ "dual object in a closed category in nLab". ncatlab.org. Retrieved 11 December 2017.
^ "텐서 카테고리"의 Pavel Eting에서 연습 2.10.4를 참조하십시오.

Dold, Albrecht; Puppe, Dieter (1980), "Duality, trace, and transfer", Proceedings of the International Conference on Geometric Topology (Warsaw, 1978), PWN, Warsaw, pp. 81–102, MR 0656721
Peter Freyd and David Yetter (1989). "Braided Compact Closed Categories with Applications to Low-Dimensional Topology". Advances in Mathematics. 77 (2): 156–182. doi:10.1016/0001-8708(89)90018-2.
André Joyal and Ross Street. "The Geometry of Tensor calculus II". Synthese Library. 259: 29–68.

이 범주 이론 관련 기사는 단조롭다.위키피디아를 확장하여 도울 수 있다.

[traces-1] Ponto, Kate; Shulman, Michael (2014). "Traces in symmetric monoidal categories". Expositiones Mathematicae. 32 (3): 248–273. arXiv:1107.6032. Bibcode:2011arXiv1107.6032P.

[2] Becker, James C.; Gottlieb, Daniel Henry (1999). "A history of duality in algebraic topology" (PDF). In James, I.M. (ed.). History of topology. North Holland. pp. 725–745. ISBN 9780444823755.

[3] "dual object in a closed category in nLab". ncatlab.org. Retrieved 11 December 2017.

[4] "텐서 카테고리"의 Pavel Eting에서 연습 2.10.4를 참조하십시오.

[1]

[2]

[3]

[4]

Search

이중 객체

네임스페이스

더

목차

동기

정의

예

듀얼이 있는 범주

트레이스

참고 항목

참조