F-알제브라

수학에서, 특히 범주 이론에서, F-알제브라는 대수 구조의 개념을 일반화한다. 형태론의 관점에서 대수 법칙을 다시 쓰는 것은 공리에서 정량화된 원소들에 대한 모든 참조를 없앨 수 있고, 이러한 대수 법칙들은 서명인 단일 functor F의 관점에서 함께 붙일 수 있다.

F-알제브라는 또한 목록과 나무와 같은 프로그래밍에 사용되는 데이터 구조를 나타내기 위해 사용될 수 있다.

주요 관련 개념은 유도 원리를 캡슐화하는 역할을 할 수 있는 초기 F-algebras와 이중구축 F-coalgebras이다.

정의

$C{\displaystyle }$ ${\displaystyle C}$이(가) 범주이고 F${\displaystyle }$: ${\displaystyle C}$→ ${\displaystyle C}$ ${\displaystyle F:$$C\rightarrow C}$ is an endofunctor of ${\displaystyle C}$, then an ${\displaystyle F}$-algebra is a tuple ${\displaystyle (A,\alpha )}$, where ${\displaystyle A}$ is an object of ${\displaystyle C}$ and ${\displaystyle \alpha }$ is a ${\displaystyle C}$-morphism ${\di$$splaystyle F(A)\오른쪽 화살표$ A$\}.$ 물체 $A{\displaystyle }$ ${\displaystyle A}$을(를) 대수 캐리어라고 한다$$. 문맥에서 허용될 경우, 알헤브라는 종종 튜플 대신 캐리어에 의해서만 언급된다.

A homomorphism from an ${\displaystyle F}$-algebra ${\displaystyle (A,\alpha )}$ to an ${\displaystyle F}$-algebra ${\displaystyle (B,\beta )}$ is a ${\displaystyle C}$-morphism ${\displaystyle f:$$다음$과 같은 A$\$오른쪽 $화살표 B}($$f$ α = ${\displaystyle \beta \beta }$ F${\displaystyle (f}$ ) ${\displaystyle f\circle \alpha =\beta \circ F(f$

이러한 형태론을 갖춘 $F{\displaystyle }$ ${\displaystyle F}$ -algebras는$$ 하나의 범주를 이룬다.

이중구조는 $F{\displaystyle }$ ${\displaystyle F}$ - coalegebras로$$, 형태론 ${\displaystyle {}^{}}$α${\displaystyle {}^{}}$α → F (${\displaystyle {}^{}{\ast }^{}}$) ${\displaystyle \alpha$$^{*}$와 함께 A$\$ {\$displaystystyle$α {}{*}:$A^{*}\오른쪽$ 화살표 $F(A^{*})}$.

예

무리

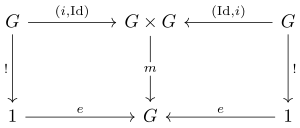
일반적으로$$ $그룹$은 법률 그룹 $m{\displaystyle }$: ${\displaystyle G}$$$${\displaystyle \times }$ G${\displaystyle }$→ ${\displaystyle G}$ ${\displaystyle m:$$G\time G}$ ,$$$m{\displaystyle }$( ${\displaystyle x}$, y${\displaystyle }$)${\displaystyle }$= ${\displaystyle x}$ ${\displaystyle \cdot }$ y ${\displaystyle m(x,y)=x\cdot y}$, ID 요소의 존재, 그룹의 각 요소에 대한 역의 존재, 연관성의 세 가지 공리를 만족한다.

이것을$$ 범주형 프레임워크에 넣으려면 $먼저{\displaystyle }$ $e{\displaystyle }$${\displaystyle (}$ ${\displaystyle \to }$ )$$=${\displaystyle 1}$ ${\displaystyle e$$:1$$(**)=1}$$및{\displaystyle }$i :${\displaystyle G}$ → ${\displaystyle G}$${\$$displaystyle i:$$G\rightarrow G}$ with ${\displaystyle i(x)=x^{-1}}$. Here ${\displaystyle 1}$ denotes the set with one element ${\displaystyle 1=\left\{*\right\}}$, which allows one to identify elements ${\displaystyle x\in G}$ with morphisms ${\displaystyle 1\rightarrow G}$.

그런 다음, 그룹의 공리를 함수의 관점에서 쓸 수 있다(존재하는 정량자가 없는 방법에 주목한다).

• ${\displaystyle \forall x\in G,\forall y\in G,\forall z\in G,m(m(x,y),z)=m(x,m(y,z))}$,
• ${\displaystyle \mathrm{\forall }}$ ${\displaystyle x}$ ${\displaystyle \in }$ ${\displaystyle G}$, m (${\displaystyle e}$ (${\displaystyle (}$ ) , x${\displaystyle }$)${\displaystyle }$= m${\displaystyle }$( ${\displaystyle x}$, e ($=$ ) = ${\displaystyle x}$ ( x , ${\displaystyle e}$ ) = x ${\fall x\in G,m(e(*),x)=m(x,e(*)=x$
• ${\displaystyle \mathrm{\forall }}$ ${\displaystyle x}$ ${\displaystyle \in }$ ${\displaystyle G}$, m${\displaystyle }$(${\displaystyle i}$( ${\displaystyle x}$ ) ,${\displaystyle }$x${\displaystyle }$)${\displaystyle }$= ${\displaystyle m}$( ${\displaystyle x}$, ${\displaystyle i}$)${\displaystyle }$= ${\displaystyle e}$ ($∗$ ${\displaystyle )}$ {\$fall$ x$\in$ G$,m(x$),x)=$m(x)=$m($x,i(x)=e$

그런 다음 이를 정류 다이어그램으로 표현할 수 있다.^[1]

$이제{\displaystyle }$ coproduct(세트 분리 결합)를 사용하여 다음 세 가지 형태(α${\displaystyle }$= e${\displaystyle }$+ ${\displaystyle i}$+ ${\displaystyle m}$ ${\displaystyle \alpha =e+i+m})$를 하나로$$ 접착하십시오.

${\displaystyle {\begin{matrix}\alpha :{1}+G+G\time G&\to &G,\*&\\mapsto &1,\x^{-1},\x(x,y)&\mapsto &x\cdot y.\end{{11}}}$

따라서 $그룹$은 $F{\displaystyle }$ ${\displaystyle F}$ -algebra이고$$ 여기서 F ${\displaystyle F}$은 ${\displaystyle \mathrm{functor}}$ $F{\displaystyle }$(G )${\displaystyle }$=${\displaystyle }$1${\displaystyle }$+ ${\displaystyle G}$+ G ${\displaystyle \times }$ G(\$displaystyle$ F$(G)=1+G+G\times G}$이다$.$ 그러나 그 반대는 반드시 사실인 것은 아니다. 일부 $F{\displaystyle }$ ${\displaystyle F}$ -algebra에서$$ $F{\displaystyle }$ ${\displaystyle F}$이(가) $functor{\displaystyle }$ F${\displaystyle (G)}$= ${\displaystyle 1}$+ G${\displaystyle }$+ ${\displaystyle G}$ ${\displaystyle \times }$ G ${\displaystyle F(G)=1+G+G\time G}$은 그룹이$$ 아니다.

위의 구성은 유한한 제품과 단자 객체 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$을(를) 가진 임의의 범주에 걸쳐 그룹 객체를 정의하는데 사용된다.$$범주가 유한한 결합체를 인정할 때 그룹 객체는 $F{\displaystyle }$ ${\displaystyle F}$ -algebras이다$$. 예를 들어 유한집단은 유한집합 범주에서 $F{\displaystyle }$ ${\displaystyle F}$ -algebras이고$$, Lie 그룹은 평활지도가 있는 평활다지관 $범주$에서 F ${\displaystyle F}$ -algebras이다$$.

대수구조

유니버설 대수보다 한 발 앞서 가는 대부분의 대수 구조는 F-알제브라다. 예를 들어, 아벨리아 그룹은 그룹과 동일한 functor F(G) = 1 + G + G×G에 대한 F-algebras이며, 공통성에 대한 추가 공리는 m∘t = m이며, 여기서 t(x,y) = (y,x)는 GxG의 전치물이다.

모노이드(monoids)는 F(M) = 1 + M×M의 F-algebras이다. 같은 맥락에서, 세미그룹들은 F(S) = S×S의 F-algebras이다.

Rings, domains and fields are also F-algebras with a signature involving two laws +,•: R×R → R, an additive identity 0: 1 → R, a multiplicative identity 1: 1 → R, and an additive inverse for each element -: R → R. As all these functions share the same codomain R they can be glued into a single signature function 1 + 1 + R + R×R + R×R → R, with axioms 연관성, 분배성 등을 표현한다. 이렇게 하면 1 + 1 + R + R×R + R×R + R×R이 있는 세트의 범주에 링 F-알제브라가 된다.

또는 아벨 그룹 범주에서 functor F(R) = 1 + R×R을 볼 수 있다. 그런 맥락에서 곱셈은 동형성(homorphism)으로, 정확하게 분포 조건인 m(x + y, z) = m(x,z) + m(x,y + z) = m(x,y + z) = m(x,y) + m(x,z)을 의미한다. 따라서 반지는 두 개의 공리(복수에 대한 연관성과 정체성)를 만족하는 아벨리아 그룹의 범주 위에 있는 기호 1 + R×R의 F-알제브라이다.

벡터 공간과 모듈을 살펴보면 시그니처 펑터에는 스칼라 곱셈 k×E → E가 포함되며, 시그니처 F(E) = 1 + E + k×E는 필드 또는 링의 범주에 걸쳐 k에 의해 파라메트리된다.

Algebras over a field can be viewed as F-algebras of signature 1 + 1 + A + A×A + A×A + k×A over the category of sets, of signature 1 + A×A over the category of modules (a module with an internal multiplication), and of signature k×A over the category of rings (a ring with a scalar multiplication), when they are associative and unitary.

격자

모든 수학적 구조가 F-알제브라는 아니다. 예를 들어 포셋 P는 하위 객체 분류자(세트 범주에서 Ω = {0,1}, s(x,y)=정확히 x≤y일 때 1)에서 형태론 s:P × P → Ω으로 범주형 용어로 정의할 수 있다. 포셋을 정의하기 위해 형태론 s를 제한하는 공리는 형태론의 관점에서 다시 쓰여질 수 있다. 그러나 s의 코도마인은 P가 아닌 Ω이므로 F-알지브라(F-algebra)는 아니다.

그러나 격자는 두 원소마다 우월성과 최소치를 갖는 부분적인 순서, 특히 전체 순서는 F-알제브라다. 이는 그것들이 x∨y = inf(x,y)와 x∧y = sup(x,y)와 같은 대수적 연산의 관점에서 동등하게 정의될 수 있기 때문이며, 특정한 공리(공칭성, 연관성, 흡수성, 공리력)를 따르기 때문이다. 따라서 그것들은 P x P + P x P의 F-algebras이다. 격자 이론은 종종 순서 이론과 보편적 대수학 둘 다에 끌린다고 한다.

반복

세트$$ $X{\displaystyle }$ ${\displaystyle X}$을(를) ${\displaystyle 1}$+ X ${\$displaystyle X}에 전송하는 $\mathrm {\bf${Set$} \$mathrm {\$bf$ {$Set$}} \$displaystyle 1+X}$\$competector$ $F{\displaystyle }$: ${\displaystyle \mathbf{S}}$ e ${\$ t}을(으)로 간주한다. 여기서 $S{\displaystyle \mathbf{}}$ ${\displaystyle \mathbf{e}}$ ${\displaystyle \mathbf{t}}$ ${\$은 집합의 범주를 나타내고$,{\displaystyle }$ + ${\displaystyle +}$은 분리 유니언에서 주어지는 통상적인 조합물을 나타내며$$$$, $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$은 단자 객체(즉, 모든 싱글톤 세트)이다$$. Then, the set ${\displaystyle \mathbb {N} }$ of natural numbers together with the function ${\displaystyle [\mathrm {zero} ,\mathrm {succ} ]:1+\mathbb {N} \to \mathbb {N} }$—which is the coproduct of the functions ${\displaystyle \mathrm {zero} :1\mapsto 0}$ and $$${\displaystyle \mathrm{s}}$ ${\displaystyle \mathrm{u}}$ ${\displaystyle \mathrm{c}}$: ${\displaystyle n}$ ${\displaystyle \mapsto }$ ${\displaystyle \mathrm{n}}$+ 1 ${\displaystyle \mathrm {such} :n\mapsto n+1}$는 F-algebra이다.

초기 F-알지브라

주어진 엔도프터 F에 대한 F-algebras 범주에 초기 물체가 있으면 초기 대수라고 한다. 위의 예에서$$ 대수$({\displaystyle N\mathbb{}}$,${\displaystyle }$[ z ${\displaystyle e\mathrm{}}$ ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{o}}$, ${\displaystyle s\mathrm{}}$ ${\displaystyle \mathrm{u}}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle ]}$) ${\displaystyle(\mathb {N}, [\mathrm {zero},\mathrm {such} ])$은 초기 대수학이다. 목록과 나무와 같이 프로그래밍에 사용되는 다양한 유한 데이터 구조는 특정 엔드폰터의 초기 알제브라로 얻을 수 있다.

functor F와 함께 최소 고정 점 구조를 사용하여 정의한 형식은 파라메트릭성이 형식을 유지한다면 초기 F-algebra로 간주할 수 있다.^[2]

유니버설 대수학도 참조하십시오.

단자 F-석탄재

이중으로, 가장 큰 고정점 개념과 단자 F-석탄점 사이에 유사한 관계가 존재한다. 이는 강력한 표준화 속성을 유지하면서 잠재적으로 무한 확장 가능한 개체를 허용하는 데 사용될 수 있다.^[2] 강력하게 정상화된 Charity 프로그래밍 언어(즉, 각 프로그램이 종료됨)에서 코인 유도 데이터 유형을 사용하여 놀라운 결과를 얻을 수 있으며, 검색 구성의 정의가 Ackermann 기능과 같은 "강력한" 기능을 구현할 수 있다.^[3]

참고 항목

• 알헤브라스(모나드용
• 대수 데이터 유형
• 카타모르피즘
• 다이얼게브라

메모들

참조

• Pierce, Benjamin C. (1991). "F-Algebras". Basic Category Theory for Computer Scientists. ISBN 0-262-66071-7.
• Barr, Michael; Wells, Charles (1990). Category theory for computing science. New York: Prentice Hall. p. 355. ISBN 0131204866. OCLC 19126000.

외부 링크

• Varmo Vene에 의한 유도형 및 유도형(Wayback Machine에서 보관된 2020-11-30)을 사용한 범주형 프로그래밍
• 필립 와들러: 재귀형 무료! (Wayback Machine에 보관된 2020-11-30) 글래스고 대학교, 1990년 6월. 초안
• CLiki의 대수 및 콜지브라(Archive 2019-04-27, 웨이백 머신에 보관)
• Jacobs, J.러튼: (Co) 알제브라스 및 (Co) 인덕션에 대한 튜토리얼. 유럽 이론 컴퓨터 과학 협회 회보, vol. 62, 1997, 웨이백 기계에 2021-02-12 보관
• Bartosz Milewski의 F-Algebras 이해(Wayback Machine에서 2020-08-04년 자료 보관)