동형성

대수학에서 동형체(同形體)는 같은 유형의 두 개의 대수 구조(예: 두 개의 그룹, 두 개의 고리 또는 두 개의 벡터 공간) 사이에 있는 구조를 보존하는 지도다. 동형사상이라는 단어는 고대 그리스어에서 유래되었다. ὁμός (homos)는 "same"을 의미하고 μ μ (모프)는 "형식" 또는 "shape"을 의미한다. 그러나 이 단어는 '동일한'^[1]을 의미하는 μὁς과 '동일한'을 의미하는 독일어 ä리히의 (잘못된) 번역 때문에 수학에 도입된 것으로 보인다. "동형주의"라는 용어는 독일의 수학자 펠릭스 클라인(1849–1925)의 덕택으로 여겨졌던 1892년에 이르면 나타났다.^[2]

벡터 공간의 동형성을 선형지도라고도 하며, 이들의 연구는 선형대수의 대상이다.

동형성의 개념은 형태주의라는 이름으로, 기초적인 집합이 없거나 대수학적이지 않은 많은 다른 구조로 일반화되었다. 이러한 일반화는 범주론의 출발점이다.

동형사상도 이형상, 내형상, 자동형상 등일 수 있다(아래 참조). 이들 각각은 어떤 종류의 형태론에도 일반화될 수 있는 방식으로 정의될 수 있다.

정의

동형성(同形性)은 구조물의 연산을 보존하는 (동일한 이름의) 형태의 두 대수구조 사이의 지도다. 이것은 지도 $f{\displaystyle }$ :${\displaystyle A}$→ B ${\디스플레이 스타일$ f$:$두 세트 $사이$의 $A\to B$$},$$B{\displaystyle }$ ${\displaystyle \cdot }$이(가$){\displaystyle }$ 구조의 작동(간소화를 위해 여기에 제공됨, 2진수 작업으로 제공됨)인$$ 경우, 동일한 구조를 장착한$$ B$${\$displaystyle B}$ 사이 A\to B}.

${\displaystyle f(x\cdot y)=f(x)\cdot f(y)}$

$모든{\displaystyle }$ 쌍 $x{\displaystyle }$ ${\displaystyle$ x$\},$ y ${\displaystyle y$$}$에 대해$.$ 종종 f {\$displaystyle f}$이(가$)$ 작업을 보존하거나$$ 작업과 호환된다고 한다$.$^{[note 1]}

공식적으로 지도 $f{\displaystyle }$: ${\displaystyle A}$→ B ${\디스플레이 스타일$ f$:$$A\to B}$은(는$$) $A{\displaystyle }$ ${\displaystyle A}$ 및$$ $B{\displaystyle }$ ${\displaystyle B}$에 정의된 아리티$$k의 $\mu {\displaystyle }$ {\$displaystyle \mu }$을(를) 보존한다$$.

${\displaystyle f(\mu _{A}(a_{1},\ldots ,a_{k}),=\mu _{B}(f_{1}),\ldots ,f(a_{k}),}$

$모든{\displaystyle }$ 요소 $a{\displaystyle {}_{}}$. ${\displaystyle .,}$ ${\displaystyle A_{}}$ ${\displaystyle A}$의 ${\displaystyle {}_{}}$ ${\$$\}\}.$

동형성에 의해 보존되어야 하는 수술은 상수인 0-ary 연산을 포함한다. 특히 구조물의 종류에 따라 신분요소가 필요한 경우, 제1구조물의 신분요소를 제2구조물의 해당 신분요소에 매핑해야 한다.

예를 들면 다음과 같다.

• semigroup homoporphism은 semigroup 운영을 보존하는 semigroups 사이의 지도다.
• 모노이드 동형성(monoid homorphism)은 모노이드 연산을 보존하고 첫 번째 모노이드의 아이덴티티 요소를 두 번째 모노이드의 아이덴티티 요소(identity 요소는 0-ari operation)에 매핑하는 모노이드 사이의 맵이다.
• 집단 동형성(同形性)은 집단 운영을 보존하는 집단 간의 지도다. 이는 집단 동형성이 첫 번째 그룹의 정체성 요소를 두 번째 그룹의 정체성 요소에 매핑하고, 첫 번째 그룹의 요소와 이 요소의 이미지의 반전에 매핑한다는 것을 암시한다. 따라서 그룹 간의 세미그룹 동형주의는 반드시 집단 동형성이다.
• 고리 동형성(ling homoporphism)은 고리 덧셈, 고리 곱셈, 곱셈을 보존하는 고리 사이의 지도다. 승법정체성 보존 여부는 사용 중인 링의 정의에 따라 달라진다. 승수 정체성이 보존되지 않으면 rng 동형성이 있다.
• 선형 지도는 벡터 공간의 동형성, 즉 아벨 그룹 구조와 스칼라 곱셈을 보존하는 벡터 공간 사이의 집단 동형성이다.
• 모듈 사이의 선형 지도라고도 하는 모듈 동형성은 유사하게 정의된다.
• 대수동형성(大學同形性)은 대수 연산을 보존하는 지도다.

대수적 구조는 둘 이상의 연산을 가질 수 있으며, 각 연산을 보존하기 위해서는 동형성이 요구된다. 따라서 일부 작업만 보존하는 지도는 구조물의 동형성이 아니라 보존된 작업만을 고려하여 얻은 하부 구조물의 동형성일 뿐이다. 예를 들어, 신분적 요소가 아닌 단조적 연산을 보존하는 모노이드 사이의 지도는 단조적 동형성이 아니라 단지 세미그룹 동형성일 뿐이다.

작전에 대한 표기법은 동형성의 출처와 대상에서 동일할 필요는 없다. 예를 들어, 실수는 덧셈을 위해 그룹을 형성하고, 양의 실수는 곱셈을 위한 그룹을 형성한다. 지수함수

${\displaystyle x\mapsto e^{x}}$

만족시키다

${\displaystyle e^{x+y}=e^{x}e^{y}}}$

그리고 따라서 이 두 집단 사이의 동형상이다. 역함수인 자연 로그가 만족하므로 이형성(아래 참조)까지 된다.

${\displaystyle \ln(xy)=\ln(x)+\ln(y),}$

또한 집단 동형상이다.

예

실제 숫자는 덧셈과 곱셈을 모두 가진 고리다. 모든 2×2 행렬의 집합은 또한 매트릭스 덧셈과 매트릭스 곱셈에서 링이다. 이 링들 사이의 함수를 다음과 같이 정의하면:

${\displaystyle f(r)={\pmatrix}r&0\\0&r\end{pmatrix}}}$

여기서 r은 실제 숫자이고, f는 반지의 동형상이다. f는 두 가지 덧셈을 모두 보존하기 때문이다.

${\displaystyle f(r+s)={\pmatrix}r+s&#0\#0&r+s\end{pmatrix}={pmatrix}r&0\r\end{pmatrix}+{pmatrix}s&#0\s\end{pmatrix}=f(r)+fs}$

및 곱하기:

${\displaystyle f(rs)={\pmatrix}rs&0\\0&rs\end{pmatrix}{pmatrix}r&0\r\end{pmatrix}{pmatrix}s&0\s\end{pmatrix}=f(r)\,f(s).}$

또 다른 예로, 0이 아닌 숫자들은 0이 아닌 실제 숫자와 마찬가지로 곱셈의 작동 하에서 그룹을 형성한다. (영(0)은 그룹의 원소에 필요한 승법 역이 없으므로 두 그룹에서 모두 제외되어야 한다. 0이 아닌 복합 번호에서 0이 아닌 실제 번호로 $기능$ f ${\displaystyle f}$ 정의

${\displaystyle f(z)= z .}$

즉, $f{\displaystyle }$ ${\displaystyle f}$은 복잡한 $숫자{\displaystyle }$ z ${\displaystyle z}$의 절대값(또는 계수)이다$.$ 그러면 $f{\displaystyle }$ ${\displaystyle f}$은 곱셈을 보존하기 때문에 그룹의 동형성이다$$.

${\displaystyle f(z_{1}z_{2})=z_{1}z_{2} = z_{1}z_{2} = z_{1} z_{2} =f(z_{1}f(z_{2}).}$

f는 다음과 같은 추가사항을 보존하지 않기 때문에 (복잡한 숫자에서 실제 숫자로) 반지의 동형성으로 확장할 수 없다는 점에 유의하십시오.

${\displaystyle z_{1}+z_{2} \neq z_{1} + z_{2} .}$

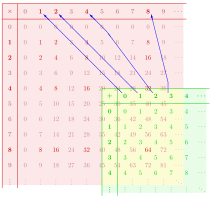
As another example, the diagram shows a monoid homomorphism ${\displaystyle f}$ from the monoid ${\displaystyle (\mathbb {N} ,+,0)}$ to the monoid ${\displaystyle (\mathbb {N} ,\times ,1)}$. Due to the different names of corresponding operations, the structure preservation properties satisfied by ${\displaystyle }$$f$ (${\displaystyle x}$+ y${\displaystyle }$)${\displaystyle }$$=$ ${\displaystyle f}$( x ) x ${\displaystyle f}$( ${\displaystyle y}$ ) = f ( ${\displaystyle x}$) ${\displaystyle \times }$ f ( y${\displaystyle }$) ${\displaystyle f(x+y)=$$f{\displaystyle }$$(x)\f$(${\displaystyle \mathrm{y}}$$)}$ 및 f$$${\displaystyle }$( 0${\displaystyle }$)${\displaystyle }$= 1 ${\displaystyle f(0)=1$

필드 $F{\displaystyle }$ ${\displaystyle F}$에 대한 $합성{\displaystyle }$ 대수 A ${\displaystyle A}$에는 $N{\displaystyle }$ : A${\displaystyle }$→ ${\displaystyle F}$ ${\displaystyle$ N$:$라고 $하는$ 2차 형식이 있다.$A$$\$$to F$ $이것$은 A {\$displaystyle A}$의 곱셈 그룹에서 $F{\displaystyle }$ ${\displaystyle F}$의 곱셈 그룹에 이르는$$ 동형상 집단이다$.$

특수 동형성

몇몇 종류의 동형체들은 특정한 이름을 가지고 있는데, 이것은 일반적인 형태론에도 정의된다.

이소모르퍼시

같은 유형의 대수구조들 사이의 이형성은 일반적으로 비주사적 동형성으로 정의된다.^{[3]: 134 [4]: 28}

보다 일반적인 범주 이론의 맥락에서 이소모르피즘은 또한 형태론인 역성을 갖는 형태론으로서 정의된다. 대수 구조의 특정한 경우, 두 정의는 기초 집합을 갖는 비알제브라 구조물에 대해서는 다를 수 있지만 동등하다.

더 정확히 말하자면

${\displaystyle f:A\to B}$

( hom)동형주의, 동형성이 존재한다면 역행하는 것이다.

${\displaystyle g:B\to A}$

그런

${\displaystyle f\circg=\operatorname {Id} _{B}\qquad {\text{and}\qquad g=\circuffername {Id} _{A}.}$

$A{\displaystyle }$ ${\displaystyle A}$ 및$$ $B{\displaystyle }$ ${\displaystyle B}$에 기본 집합이 ${\displaystyle \mathrm{있고<img\; alt="B"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/47136aad860d145f75f3eed3022df827cee94d7a"\; style="vertical-align:\; -0.338ex;\; width:1.764ex;\; height:2.176ex;">}}$ f${\displaystyle }$: ${\displaystyle A}$→ B ${\displaystyle f:$$A{\displaystyle }$$\to B}$에는 역 $g{\displaystyle }$ ${\displaystyle g}$이$($가) 있고, f ${\displaystyle f}$은(는) 편향적이다. In fact, ${\displaystyle f}$ is injective, as ${\displaystyle f(x)=f(y)}$ implies ${\displaystyle x=g(f(x))=g(f(y))=y}$, and ${\displaystyle f}$ is surjective, as, for any ${\displaystyle x}$ in ${\displaystyle B}$, one has ${$$\displaystyle x=f(g(x))}$및 $x{\displaystyle }$ ${\displaystyle x}$은(는) $A{\displaystyle }$ ${\displaystyle A}$ 요소의 이미지 입니다$.$

반대로 $f{\displaystyle }$: ${\displaystyle A}$→ B ${\displaystyle f:$$A\to B}$은(는) 대수적 구조 사이의 편향적 동형상이다. ${\displaystyle \mathrm{let}}$ g${\displaystyle }$: ${\displaystyle B}$→ A ${\displaystyle g:$$B\to A}$ be the map such that ${\displaystyle g(y)}$ is the unique element ${\displaystyle x}$ of ${\displaystyle A}$ such that ${\displaystyle f(x)=y}$. One has ${\displaystyle f\circ g=\operatorname {Id} _{B}{\text{ and }}g\circ f=\operatorname {Id$$} _{A}}}$ 그리고$$ 그것은 g가 동형상이라는 것을 보여줄 뿐이다. structure$${\$displaystyle$ $*\}{\displaystyle }$이$($가$$) 구조의 이진 연산인 경우$,$ $모든{\displaystyle }$ 쌍$$x {\$displaystyle$$x{\displaystyle }$$},$$$y {\$displaystyle$ y$}$에 대해 다음이 있음

${\displaystyle g(x*_{B}y)=g(f(g(x)))*_{B}f(y)=g(f(g)(x)*_{A}g(y))=g(x)*_{A}g(y),}$

$g{\displaystyle }$ ${\displaystyle g}$은(는) 따라서 $\ast {\displaystyle }$. {\$displaystyle *.}$과(와) 양립할 수 있다$$. 그 증거는 어떤 경지에 대해서도 유사하므로$$, $g{\displaystyle }${\$displaysty g}$이(가) 동형성임을 알 수 있다.

이 증거는 비알브레이크 구조에는 적용되지 않는다. 예를 들어 위상학 공간의 경우 형태론은 연속형 지도가 되며, 생물학적 연속형 지도의 역행성이 반드시 연속형인 것은 아니다. 위상 공간의 이형성(異形性)은 동형성(同形性) 또는 이형성(異形性) 지도(異形性)이라 불리며, 따라서 이형성(異形性)은 편향성 연속 지도(異形性)이며, 이형성(異形性)은

내형성

내형성(endomorphism)은 동형성(homomorphism)이며, 그 영역은 코도메인과 같으며, 더 일반적으로는 근원이 대상과 동일한 형태주의를 말한다.^{[3]: 135}

대수적 구조 또는 범주의 물체의 내형성은 구성 하에서 단모형을 형성한다.

벡터 공간이나 모듈의 내형성은 고리를 형성한다. 벡터 공간이나 유한차원의 자유 모듈의 경우, 기초의 선택은 내형성 링과 같은 차원의 사각 행렬 링 사이에 고리 이형성을 유도한다.

자동형성

자동형성(omotorphism)은 또한 이형성(異形性)인 내형성(內形性)^{[3]: 135} 이다.

대수적 구조 또는 범주의 물체의 자동형은 구성 중인 그룹을 형성하는데, 이를 구조의 자동형 집단이라고 한다.

이름을 받은 많은 집단은 어떤 대수적 구조의 자동형 집단이다. 예를 들어 일반 선형 그룹 ${\displaystyle {\mathrm{GL}}_{}}$ ${\displaystyle n_{}}$ ${\displaystyle (k}$) ${\displaystyle \operatorname {GL} _{n}(k)}$은 필드 $k{\displaystyle }$ ${\displaystyle k}$ 위에$$ 있는 차원 $n{\displaystyle }$ ${\displaystyle n}$의 벡터 공간의 자동형 그룹이다$.$

분야별 오토모르피즘 집단은 다항식의 뿌리를 연구하기 위해 에바리스테 갈루아가 도입한 것으로 갈루아 이론의 근간이다.

단동형성

대수적 구조의 경우, 단형성은 일반적으로 주입성 동형성으로 정의된다.^{[3]: 134 [4]: 29}

카테고리 이론의 보다 일반적인 맥락에서, 단형주의는 취소할 수 있는 상태로 남겨진 형태주의로 정의된다.^[5] 즉, (호모)형상${\displaystyle }f{\displaystyle }$ :${\displaystyle A}$ → ${\displaystyle B}$ ${\displaystyle$ f$:$$A\to B$$}$은(는) 다른 $개체{\displaystyle }$ C ${\displaystyle C}$에서 $A{\displaystyle }$ ${\displaystyle A}$까지의 어떤$$ 쌍 $g$${\displaystyle h}$에 대해$,$ $f{\displaystyle }$ ${\displaystyle \circ }$ ${\displaystyle g}$= f$$${\displaystystyle$ f$\circirc g=\$$circh$을$($)로 내포함$$).

이 단형성의 두 가지 정의는 모든 일반적인 대수 구조에 대해 동등하다. 보다 정확히 말하면, 그것들은 모든 동형성이 단형성이며, 보편대수의 다양성에 대해서는 아무런 제약 없이 연산 및 공리(식별)가 정의되는 대수적 구조(수치적 구조)가 된다(승수적 역행위는 단형 연산 또는 단형연산으로 정의되기 때문에 장(場)은 다양성이 아니다). 두 경우 모두 0이 아닌 원소에 대해서만 정의되는 곱셈의 속성).

특히, 단형성의 두 가지 정의는 세트, 마그마스, 세미그룹, 모노이드, 그룹, 링, 필드, 벡터 공간 및 모듈에 동등하다.

분할 단형주의는 좌 역성을 갖는 동형성이며, 따라서 그 자체가 그 다른 동형성의 우측 역이다. That is, a homomorphism ${\displaystyle f\colon A\to B}$ is a split monomorphism if there exists a homomorphism ${\displaystyle g\colon B\to A}$ such that ${\displaystyle g\circ f=\operatorname {Id} _{A}.$$}}$ 분열된$$ 단성형은 항상 단성형이며, 단성형의 두 가지 의미에 모두 해당된다. 세트와 벡터 공간의 경우, 모든 단성형은 분할된 단성형이지만, 이 특성은 대부분의 일반적인 대수학적 구조에 대해 보유하지 않는다.

에피모르퍼시즘

대수학에서 경구체는 흔히 굴절성 동형성으로 정의된다.^{[3]: 134 [4]: 43} 반면 범주론에서 인식론은 오른쪽 취소형 형태론으로 정의된다.^[5] 즉, (호모)형상${\displaystyle }f{\displaystyle }$ :${\displaystyle A}$ → ${\displaystyle B}$ ${\displaystyle$ f$:$$A{\displaystyle }$$\to B}$은(는) $쌍{\displaystyle }$ $g{\displaystyle }$ ${\displaystyle g$ h ${\displaystyle B}$에서 다른 개체 $C{\displaystyle }$ ${\displaystyle C}$까지의 $형태변환$에 대해$,$ $동일{\displaystyle }$ g${\displaystyle f}$f = $f$ f$${\$displaystysty$ $g=$$h\$$circ$$f}$을 암시하는 경시사이다$$$.$

허탈적 동형성은 언제나 취소할 수 있는 것이 맞지만, 대수학적 구조에 대해서는 그 반대가 항상 사실인 것은 아니다. 단, 에피모르피즘의 두 가지 정의는 집합, 벡터 공간, 아벨리아 그룹, 모듈(증거는 아래 참조), 그룹과 동일하다.^[6] 모든 수학에서, 특히 선형대수학 및 동질대수학에서 이러한 구조의 중요성은 두 가지 비등등한 정의의 공존을 설명할 수 있다.

비주사적 경각성이 존재하는 대수적 구조에는 세미그룹과 링이 포함된다. 가장 기본적인 예는 이성적인 숫자에 정수를 포함시키는 것인데, 이것은 고리와 승수적 의미집단의 동형성이다. 두 구조에서 모두 그것은 단형주의와 비굴절적 경시론이지만 이형성은 아니다.^[5][7]

이 사례의 넓은 일반화는 곱셈 집합에 의한 링의 국산화다. 모든 국산화란 고리 인식론인데, 일반적으로는 허탈하지 않다. 국소화가 정류 대수학 및 대수학 기하학에서 기본이기 때문에, 이것은 이러한 영역들에서 일반적으로 오른쪽 취소 가능한 동음이의어로서 인식의 정의가 선호되는 이유를 설명할 수 있다.

분할 인식론은 우측 역행성을 갖는 동형성이며, 따라서 그 자체도 그 다른 동형성의 좌측 역행이다. That is, a homomorphism ${\displaystyle f\colon A\to B}$ is a split epimorphism if there exists a homomorphism ${\displaystyle g\colon B\to A}$ such that ${\displaystyle f\circ g=\operatorname {Id} _{B}.$$}}$ 분열된$$ 인식론은 인식론의 두 가지 의미에 대해 항상 인식론이다. 세트와 벡터 공간의 경우, 모든 경구체는 분할 경구형이지만, 이 특성은 대부분의 일반적인 대수학적 구조에 대해 유지되지 않는다.

요컨대, 사람은

${\displaystyle {\text{properimorpism}\properties {\text{epimorphism(굴절)}}}\cHB{\텍스트{epimorphism(오른쪽 취소 가능)}};}$

마지막 암시는 세트, 벡터 공간, 모듈 및 아벨 그룹과 동등하다. 첫 번째 암시는 세트와 벡터 공간의 동등성이다.

커널

${\displaystyle \mathrm{모든}}$ 동형상 $f{\displaystyle }$: ${\displaystyle X}$→ Y ${\displaystyle f:X\to Y}$은${\displaystyle (}$는$)$ $f{\displaystyle (}$) = $b$ ${\displaystyle a\$$sim$ b$}$에 의한$$${\displaystyle }$동등성 $관계$ ~ {\$displaystyle \$$sim$ b$}$을$($는$)$로 정의한다$.$ 관계${\displaystyle }$~ ${\displaystyle \sim }$은(는) $f{\displaystyle }$ ${\displaystyle$ $f$$}$의 커널이라고 불리며$$$,$ $X{\displaystyle }$ ${\displaystyle$ X$}$에서 일치된 관계다$.$ The quotient set ${\displaystyle X/{\sim }}$ can then be given a structure of the same type as ${\displaystyle X}$, in a natural way, by defining the operations of the quotient set by ${\displaystyle [x]\ast [y]=[x\ast y]}$, for each operation ${\displaystyle \ast }$ of ${\disp$$레이스타일 X$ $그렇다면{\displaystyle }$ 동형상 $f{\displaystyle }$ ${\displaystyle$ f$}$에 따른$$ Y ${\displaystyle Y}$의 X ${\displaystyle X}$의 이미지는 $반드시{\displaystyle }$ X${\displaystyle }$/${\displaystyle }$~ ${\displaystyle$ X$/\!\sim$}에 이형상이다$.$ 이 사실은 이형상주의 이론 중 하나이다.

대수적 구조가 일부 연산을 위한 그룹인 경우, 이 연산의 ID 요소의 동등성 등급 $K{\displaystyle }$ ${\displaystyle K}$은 동등성 관계를 특징짓는 데 충분하다. 이 경우 동등성 관계에 의한 지수는 ${\displaystyle X}$/ K ${\displaystyle X/K}($일반적으로 "${\displaystyle }$ ${\displaystyle X}$ mod$$ $K{\displaystyle }$ ${\displaystyle$ K$}"$로 읽음)로 표시된다.$$ $또한{\displaystyle }$ 이 경우 f ${\displaystyle f}$의 커널이라고 하는 것은${\displaystyle }$~ ${\displaystyle \sim }$이 아니라$$K ${\displaystyle K}$이다$.$ 주어진 형태의 대수구조의 동형성의 낟알은 자연적으로 어떤 구조를 갖추고 있다. 이 커널의 구조 유형은 고려된 구조와 동일하지만, 아벨 그룹, 벡터 공간 및 모듈의 경우 다르며, 그룹 동형성의 커널에 대한 정상 부분군 및 링 동형성의 커널에 대한 이상(비 커맨티브 링의 경우, ke)과 같은 다른 경우에 특정한 이름을 받았다.rnels는 양면적인 이상이다.

관계 구조

모델 이론에서 대수적 구조의 개념은 운영과 관계를 모두 포함하는 구조로 일반화된다. L은 함수 기호와 관계 기호로 구성된 시그니처가 되고, A, B는 두 개의 L-구조로 구성된다. 그렇다면 A에서 B까지의 동형성은 A의 영역에서 B의 영역으로 h를 매핑하여 다음과 같이 하는 것이다.

• h(F^A(a₁,…,a_n) = 각 n-ari 함수 기호 F(L)에 대해^B F(h(a₁),…,h(a_n)
• R^A(a₁, …,a_n)은 L에서 각 n-arri 관계 기호 R에 대해^B R(h(a₁), …,h_n(a)를 의미한다.

단 하나의 이항 관계를 갖는 특별한 경우에서 우리는 그래프 동형성의 개념을 얻는다. 관계형 동형식과 이형성에 대한 자세한 설명은 다음을 참조하십시오.^[8]

형식언어론

동형체는 형식 언어의^[9] 연구에도 사용되며 종종 간략하게 형태론이라고 일컬어진다.^[10] 알파벳 σ과₁ σ을₂ 주어, σ에서₁^∗ h(uv) = h(u)h(v)가 모든 u와 v에 대해 h(u) h(v)가 되는 함수 h : → → σ을₁^∗₂^∗ σ에서는₁^∗ 동형성이라고 부른다.^{[note 2]} 만약 h가 σ에서₁^∗ 동형체이고 ε이 빈 줄을 나타내는 것이라면, σ에서₁^∗ h(x) ≠의 모든 x for에 대해 h(x) ≠을 when할 때 h를 ε 없는 동형체라고 부른다.

알파벳 σ에서 형성된 단어의 σ^∗ 집합은 σ에 의해 생성되는 자유 단조로 생각할 수 있다. 여기서 모노이드 연산은 결합이고 정체성 요소는 빈말이다. 이러한 관점에서 언어동형주의는 정확히 단성동형주의다.^{[note 3]}

참고 항목

• 연속함수
• 차이점형성
• 동형 암호화
• 동형 비밀 공유 – 단순 분산 투표 프로토콜
• 형태론

메모들

인용구

참조

• Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
• Mac Lane, Saunders (1971), Categories for the Working Mathematician, Graduate Texts in Mathematics, 5, Springer-Verlag, ISBN 0-387-90036-5, Zbl 0232.18001
• Fraleigh, John B.; Katz, Victor J. (2003), A First Course in Abstract Algebra, Addison-Wesley, ISBN 978-1-292-02496-7