패러데이 역설

패러데이 패러데이의 역설 또는 패러데이의 역설은 마이클 패러데이의 전자기유도 법칙이 부정확한 결과를 예측하는 것으로 나타나는 어떤 실험이다. 역설은 두 부류로 나뉜다.

• 패러데이의 법칙은 기전력(EMF)이 0이 될 것이라고 예측하는 것처럼 보이지만, EMF가 0이 아닌 것이 있다.
• 패러데이의 법칙은 0이 아닌 EMF가 있을 것이라고 예측하는 것처럼 보이지만 EMF는 0이다.

패러데이는 1831년 최초의 전자기 발전기나 다이너모어를 발명한 후 자신의 유도 법칙을 추론했지만, 역설에 대한 자신의 설명에는 결코 만족하지 않았다.

맥스웰-파라데이 방정식과 비교한 패러데이 법칙

패러데이 법칙(Faraday-Lenz 법칙이라고도 함)은 기전력(EMF)은 시간 t에 관하여 자속의 총 파생량에 의해 주어진다고 명시한다.

${\displaystyle {\mathcal{E}=-{\frac {d\Phi _{B}{dt},}$

여기서 $E{\displaystyle \mathcal{}}$ ${\$은(는) EMF이고 φ은_B 자속이다. 기전력의 방향은 렌츠의 법칙에 의해 주어진다. 종종 간과되는 사실은 패러데이의 법칙이 자속의 부분파생물이 아닌 총파생물에 기초하고 있다는 것이다.^[1] 이는 표면을 통과하는 총 유속이 일정하더라도 EMF가 발생할 수 있다는 것을 의미한다. 이 문제를 극복하기 위해 특별한 기술이 사용될 수 있다. Faraday의 법칙과 함께 특수 기법의 사용에 대한 섹션은 아래를 참조하십시오.

그러나 패러데이의 법칙에 대한 가장 일반적인 해석은 다음과 같다.

모든 폐쇄 회로에서 유도된 기전력은 회로에 둘러싸인 자속 변화 시간의 음과 같다.^[2][3]

이 패러데이 법전은 폐쇄 회로가 무한히 얇은 철사의 고리일 때만 엄격히 유지되며,^[4] 다른 상황에서는 무효가 된다. 그것은 패러데이의 법칙이 자속의 일부가 아닌 전체 파생상품으로 정의된다는 사실과 또한 EMF가 반드시 폐쇄된 경로에 국한된 것이 아니라 아래에서 논의한 바와 같이 방사형 구성요소를 가질 수 있다는 사실을 무시한다. 다른 버전인 Maxwell-Faraday 방정식(아래에서 설명)은 모든 상황에서 유효하며, 로렌츠 힘 법칙과 함께 사용할 경우 Faraday의 법칙의 올바른 적용과 일치한다.

맥스웰-파라데이 방정식은 시간변동 자기장이 항상 공간변동형, 비보수형 전기장을 동반하고, 그 반대의 경우도 마찬가지라는 패러데이 법칙의 일반화다. Maxwell-Faraday 방정식은 다음과 같다.

(SI 단위에서)${\displaystyle \mathrm{}}$where ${\displaystyle \partial }$이(가) 부분파생 연산자,${\displaystyle \mathrm{}}$curl ${\displaystyle \times }$ ${\displaystyle \nabla \times }$이(가) 컬 연산자, 다시$$ E(r, t)가 전기장, B(r, t) 자기장이다. 이러한 장은 일반적으로 위치 r과 시간 t의 기능이 될 수 있다.

맥스웰-파라데이 방정식은 4개의 맥스웰 방정식 중 하나로, 따라서 고전 전자석 이론에 근본적인 역할을 한다. 켈빈-스토크스 정리에도 적분 형태로 쓸 수 있다.^[8]

패러데이의 유도 법칙이 0 EMF를 예측하는 것처럼 보이지만 실제로는 0이 아닌 EMF를 예측하는 역설

이러한 역설은 일반적으로 패러데이의 법칙에서 설명한 회로의 플럭스 변화나 자기장 내 도체의 움직임에 의해 EMF가 생성될 수 있다는 사실에 의해 해결된다. 이것은 파인만에 의해 아래에 언급된 바와 같이 설명된다. A도 참조하십시오. 소머펠트, Vol III Electrodynamics Academic Press, 362페이지.

장비

실험에는 몇 가지 간단한 구성 요소가 필요하다(그림 1 참조). 원통형 자석, 전도성 림이 있는 전도성 디스크, 전도성 차축, 일부 배선 및 전류계. 디스크와 자석은 차축에 짧은 거리를 두고 장착되며, 차축에서 대칭의 축을 중심으로 자유롭게 회전할 수 있다. 전기 회로는 슬라이딩 접점을 디스크 축에 연결하고 다른 접점은 림에 연결함으로써 형성된다. 회로에 전류를 측정하기 위해 전류를 삽입할 수 있다.

절차

실험은 세 단계로 진행된다.

1. 자석은 자석이 회전하지 못하도록 잡고, 디스크는 축에 돌린다. 그 결과 전류가 직류로 등록된다. 따라서 이 기구는 다양한 명칭으로 패러데이 발생기, 패러데이 디스크 또는 동음이의 발생기(또는 단극)로 불리는 발전기 역할을 한다.
2. 자석이 축에 회전하는 동안 디스크는 정지 상태로 유지된다. 그 결과 전류계는 전류를 등록하지 않는다.
3. 디스크와 자석이 함께 회전한다. 전류계는 1단계에서와 같이 전류를 등록한다.

왜 역설적인가?

이 실험은 어떤 것이 회전해도 원반을 통과하는 유속이 같아 보이기 때문에, 첫눈에 파라다이의 전자기유도 법칙을 위반하는 것처럼 보이는 것처럼, 일부에 의해 "파라독스"로 묘사되고 있다. 따라서 EMF는 세 가지 회전 사례 모두에서 0이 될 것으로 예측된다. 아래 논의는 이러한 관점이 플럭스를 계산하기 위한 표면을 잘못 선택한 데서 비롯되었음을 보여준다.

역설은 플럭스 관점과는 조금 다르게 나타난다: 패러데이의 전자기 유도 모델에서 자기장은 철의 필링을 종이에 뿌리고 자석 근처에 붙일 때 나타나는 선과 유사하게 자속의 상상의 선으로 구성되었다. EMF는 플럭스의 절단선 속도에 비례하도록 제안된다. 만약 플럭스의 선들이 자석에 기원을 둔다고 상상된다면, 그들은 자석의 프레임에서 정지해 있을 것이고 자석을 회전시키든 원반을 회전시키든 자석에 상대적인 원반을 회전시키면 EMF가 생성되지만 둘 다 함께 회전하면 안 된다.

패러데이의 설명

패러데이의 전자기 유도 모델에서 회로는 자속선을 절단할 때 유도 전류를 받았다. 이 모델에 따르면 패러데이 디스크는 디스크나 자석이 회전할 때 작동했어야 하는데 둘 다 작동하지 않았다. 패러데이는 플럭스 라인으로 완성된 자석의 장이 자석이 회전할 때 정지해 있다고 가정함으로써 관찰과의 불일치를 설명하려고 했다(완전히 정확한 그림이지만 아마도 플럭스 선 모델에서는 직관적이지 않을 것이다). 즉, 플럭스의 선은 그 나름의 기준틀을 가지고 있다. 다음 절에서 보게 되겠지만, (전자가 발견된 이후) 현대 물리학은 플룩스 선 그림이 필요하지 않고 역설적인 것을 왜곡한다.

현대적 설명

반환 경로 고려

2단계에서는 전류가 관찰되지 않기 때문에 자장이 회전하는 자석으로 회전하지 않았다고 결론을 내릴 수 있다.(효과적이거나 상대적으로 회전하는지의 여부와 상관없이 v는 실험실 프레임에 상대적인 0이기 때문에 로렌츠 힘은 0이다. 따라서 실험실 프레임에서 측정되는 전류는 없다.) 로렌츠 방정식을 사용하여 이 역설의 설명을 함으로써 자기장이 자석으로 회전하는가에 대한 문헌상의 논쟁을 불러 일으켰다. 로렌츠 방정식에 의해 표현된 전하들에 대한 힘은 EMF가 위치한 도체에 대한 자기장(즉 실험실 프레임)의 상대적인 움직임에 따라 달라지기 때문에, 자석이 디스크와 함께 회전하지만 전압이 여전히 발생할 경우, 자장(즉 실험실 프레임)은 그에 따라 달라져야 한다고 추측되었다.e 자성 물질로 회전하지 않는 동안(물론 실험실 프레임이기 때문에), 자기장 프레임의 효과적인 정의 또는 "장치의 유효/비효율 회전"은 전도성 디스크에 대해 상대적인 움직임 없이 회전한다.

조심해 생각 만약 자기장을 갖는 자석과 자석은 디스크와 함께 회전으로 회전는 것으로 추정되었으며는 기류를 여전히, 기전력에 의해 디스크( 없는 상대 운동 그 디스크와 자석 사이에 있다.)에 있지만 외부 회로에서 어떤 사실에 상대 운동에 대한 존중과 함께 있brushes,[9]기를 연결하는 아니라 생산되어야 한다 보여 줬다t입니다그는 자석을 회전시킨다. (솔은 실험실 틀 안에 있다.)

이 메커니즘은 복귀 경로와 관련된 관찰에 동의한다: 자석의 회전에 관계 없이 디스크가 복귀 경로에 상대적으로 이동할 때마다 EMF가 생성된다. 실제로 디스크와 자석의 움직임에서 유도된 EMF를 측정하기 위해 전류 루프를 사용하는 한 자기장이 자석과 회전하는지 또는 회전하지 않는지를 알 수 없는 것으로 나타났다. (이것은 정의에 따라 다르며, 필드의 운동은 효과적으로/상대적으로만 정의될 수 있다. 필드 플럭스가 물리적 실체라는 보기를 유지하는 경우, 플럭스는 회전하거나 생성 방법에 따라 달라진다. 그러나 이것은 로렌츠 공식, 특히 v, 측정이 이루어지는 프레임에 상대적인 전하 캐리어의 속도 및 어느 틈새 시점에서든 상대성에 따라 전계 강도가 달라지는 것은 아니다.)

이 문제를 해결하기 위해 정전기 측정이나 전자 빔을 이용한 여러 실험이 제안되었지만 현재까지 성공적으로 수행된 실험은 없는 것으로 보인다.^{[citation needed]}

로렌츠 힘 사용

외부 전기장 E와 자기장 B로 인해 순간 속도 v의 전하 q 입자에 작용하는 F 힘은 로렌츠 힘에 의해 주어진다.^[10]

여기서 ×는 벡터 크로스 제품이다. 모든 굵은 글씨체는 벡터다. 점 전하의 상대론적으로 올바른 전기장은 속도에 따라 다음과 같이 변화한다.^[11]

${\displaystyle \mathbf {E} ={\frac {q}{4\pi \epsilon _{0}}}{\frac {1-v^{2}/c^{2}}{(1-v^{2}\sin ^{2}\theta /c^{2})^{3/2}}}{\frac {\mathbf {{\hat {r}}'} }{ \mathbf {r} ' ^{2}}}}$

여기서 $r{\displaystyle {\stackrel{}{\mathbf{}}}^{}}$ ${\displaystyle {\stackrel{}{\mathbf{^}}}^{}}$ ${\displaystyle {^}^{}}$ ${\$은(는) 입자의 현재(비혼합) 위치에서 필드가 측정되는 지점까지 가리키는 단위 벡터이며, $\theta$은 v ${\$과(와) $r{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}${\$displaystytype \mathbf {r}$ 사이의 각도이다$.$ 전하의 자기장 B는 다음과 같다.^[11]

${\displaystyle \mathbf {B} ={\frac {1}{c^{2}}}\mathbf {v} \time \mathbf {E}}}}$

가장 기초적인 수준에서 총 로렌츠 힘은 다른 모든 전하에서 작용하는 모든 전하의 전기장 E와 자기장 B의 누적된 결과물이다.

자석이 회전하지만 플럭스 라인이 정지해 있고 도체가 정지해 있을 때

원통형 전도성 디스크가 정지해 있지만 원통형 자기 디스크가 회전하는 특수한 경우를 고려하십시오. 그러한 상황에서 전도 디스크에서 전하의 평균 속도 v는 초기에는 0이며, 따라서 자기력 F = qv × B는 0이며, 여기서 v는 측정을 하는 프레임에 상대적인 회로의 전하 q의 평균 속도이며, q는 전자에 대한 전하량이다.

자석과 플럭스 라인이 정지해 있고 도체가 회전 중일 때

전자와 그것에 영향을 미치는 힘이 발견된 후, 역설의 미시적인 분해능이 가능해졌다. 그림 1을 참조하십시오. 기구의 금속 부분은 전도되고 있으며, 전자적 움직임으로 인한 전류를 금속 경계 내로 제한한다. 자기장에서 움직이는 모든 전자는 F = qv × B의 로렌츠 힘을 경험하며, 여기서 v는 측정이 이루어지는 프레임에 상대적인 전자의 속도, q는 전자의 전하량을 경험한다. 기억하라, "전자장의 프레임"과 같은 프레임은 없다. 프레임은 수학적 객체로서 연장된 필드나 플럭스 선이 아닌 특정 스페이스타임 포인트에 설정된다. 플럭스를 물리적 실체로 간주하거나(자기 플럭스 양자 참조), 장 운동/회전의 유효/상대적 정의를 고려한다면(아래 참조) 다른 문제다. 이 노트는 역설의 해결에 도움이 된다.

로렌츠 힘은 디스크의 평면에 있는 전자의 속도와 디스크에 정상(표면 정상)인 자기장에 모두 수직이다. 디스크의 프레임에 정지해 있는 전자는 B-필드(즉, 회전축이나 실험실 프레임, 위의 참고 사항 기억)에 상대적인 디스크와 함께 원형으로 움직이며, 따라서 방사형 로렌츠 힘을 경험하게 된다. 그림 1에서 이 힘(전자가 아닌 양전하)은 오른손 법칙에 따라 림을 향해 바깥쪽으로 향한다.

물론 전류의 원인인 이 방사적인 힘은 전자 속도의 반경 성분을 생성하여, 전자의 원형 운동에 반대되는 자체 로렌츠 힘 성분을 차례로 생성하여 디스크의 회전을 늦추려고 하지만, 전자는 전류를 통해 계속적으로 전류를 구동하는 원형 운동 성분을 가지고 있다.그는 방사상 로렌츠 힘.

패러데이 법칙에 따른 특수 기법 사용

자장이 이 경로의 평면(그 경로에 수직이 아닌 수직이 아닌)에 있기 때문에 림의 브러시에서 바깥 루프와 축을 통해 디스크의 중심까지 경로의 부분을 통과하는 유속이 항상 0이다. 따라서 경로의 이 부분을 둘러싼 통합 emf는 항상 0이다. 따라서 디스크를 가로지르는 차축에서 림의 브러시까지 경로 부분에 관심이 집중된다.

패러데이의 유도 법칙은 다음과 같이 말로 표현할 수 있다.^[12]

어떤 폐쇄 회로에서든 유도된 기전력 또는 EMF는 회로를 통과하는 자속의 시간 변화율과 동일하다.

수학적으로 이 법칙은 다음과 같이 명시되어 있다.

${\displaystyle {\mathbf {E}=-{\frac {d\Phi _{d}}{dt}}\iint _{\Sigma(t)_{\Sigma(t)}d\cdot \mathbf {B}(\mathbf {r},\t)\},},},},},},},},}$

여기서 φ은_B 플럭스(flux)이며, dA는 EMF가 발견될 주변의 루프에 의해 경계된 이동 표면 σ(t) 영역의 벡터 요소다.

플럭스 연계가 단지 디스크 면적에 곱한 B-필드인 것처럼 보이는 패러데이 디스크 발생기에 이 법칙을 어떻게 연결할 수 있을까?

한 가지 접근방식은 브러시에서 차축까지 디스크 전체에 가설적인 선을 긋고 단위 시간 당 얼마나 많은 플럭스 연동이 이 선을 통과하여 쓸리는지를 질문함으로써 "플럭스 연동의 변화율" 개념을 정의하는 것이다. 그림 2를 참조하십시오. 디스크의 반지름 R을 가정할 때 중심 각도가 θ인 디스크 섹터에는 다음 영역이 있다.

${\displaystyle A={\frac {\theta}{2\pi }}}}}{2\pi R^{2}\,}$

그래서 플럭스가 상상의 선을 스치는 속도는

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=B{\frac {dA}{dt}}=B\ {\frac {R^{2}}{2}}\ {\frac {d\theta }{dt}}=B\ {\frac {R^{2}}{2}}\omega \ ,}$

Ω = d³ / dt 회전 각도 비율 이 부호는 렌즈의 법칙에 근거하여 선택된다: 움직임에 의해 생성된 장은 회전으로 인한 유동 변화에 반대해야 한다. 예를 들어, 오른쪽 규칙에 따라 그림 2의 방사형 세그먼트가 있는 회로는 적용된 B-필드에 추가되어 플럭스 연결력을 증가시킨다. 이는 이 경로를 통과하는 유속이 회전으로 인해 감소하고 있음을 시사하므로 dθ/dt는 음수임을 의미한다.

EMF에 대한 이러한 플럭스 컷팅 결과는 단위 전하당 수행된 작업을 계산하여 최소 시험 전하가 반경 r에서 로렌츠 힘/단위 전하(v × B = Bv = BrΩ)를 사용하여 가상 라인을 통과하도록 하는 것과 비교할 수 있다.

${\displaystyle {\mathcal{E}=\int _{0}^{R}drBr\omega ={\frac {R^{2}}:B\omega \,}$

같은 결과야

회로에 의해 절단된 플럭스를 찾기 위한 위의 방법론은 경계면 σ(t)의 시간파생물을 적절하게 처리함으로써 플럭스 법칙에 공식화된다. 물론, 시간 의존적 한계가 있는 적분들의 시간 파생상품은 단순히 통합의 시간 파생상품이 아니며, 종종 잊혀지는 지점이다. 라이프니즈 적분 규칙과 로렌츠 힘을 참조하라.

표면 σ(t)을 선택할 때, 제한사항은 (i) EMF가 발견될 주변의 닫힌 곡선에 의해 제한되어야 하며, (ii) 회로의 모든 움직이는 부분의 상대적인 움직임을 포착해야 한다는 것이다. 경계 곡선이 전류의 물리적 흐름 라인에 해당한다는 것은 강조할 필요가 없다. 반면에 유도는 상대운동에 관한 것이며, 길은 어떤 상대운동도 강하게 포착해야 한다. 그림 1과 같이 현재 경로의 일부가 공간의 한 지역에 분산되어 있는 경우, 전류를 구동하는 EMF는 다양한 경로를 사용하여 찾을 수 있다. 그림 2는 두 가지 가능성을 보여준다. 모든 경로는 분명한 리턴 루프를 포함하지만, 디스크에는 기하학적으로 단순한 경로인 두 개의 경로가 표시된다. 하나는 뒤틀린 경로다. 우리는 우리가 원하는 어떤 경로든 자유롭게 선택할 수 있지만, 어떤 허용 가능한 경로의 일부는 디스크 자체에 고정되어 있고 디스크와 함께 회전한다. 플럭스는 전체 경로, 리턴 루프와 디스크 세그먼트, 그리고 그 변화율이 발견되어 계산된다.

이 예에서, 이러한 모든 경로는 동일한 플럭스 변화율, 즉 동일한 EMF로 이어진다. 이 경로의 독립성에 대한 직관력을 제공하기 위해 그림 3에서 패러데이 디스크를 스트립에 풀어서 슬라이딩 직사각형 문제와 유사하게 만든다. 슬라이딩 직사각형 케이스에서 직사각형 내부의 전류 흐름 패턴이 시간 독립적이기 때문에 회로를 연결하는 플럭스의 변화 속도와 무관하다는 것이 명백해진다. 전류가 직사각형(또는 디스크)을 통과하는 방법을 정확히 고려할 필요는 없다. 직사각형의 상단과 하단을 연결하고 직사각형과 함께 이동(디스크와 회전)하는 경로의 선택은 플럭스의 변화율을 동일하게 쓸어내고, 동일한 EMF를 예측한다. 디스크의 경우, 이 플럭스 추정의 변화율은 디스크를 선을 지나 회전하는 것에 기초하여 위에서 행한 것과 같다. 붓을 축에 끼우는 것

반환 경로가 있는 구성

이 분석에서 자석이 "움직이는" 것은 복귀 경로에서 유도되는 유동성 때문에 관련이 없다. 중요한 상대운동은 디스크와 자석의 운동이 아니라 디스크와 복귀 경로의 운동이다. 이는 반환 경로가 와이어가 아닌 다른 디스크인 수정된 패러데이 디스크를 사용하는 경우 더 명확해진다. 즉, 두 개의 전도성 디스크를 같은 축에 서로 바로 옆에 장착하고 중앙과 원주에 슬라이딩 전기 접점을 갖도록 한다. 전류는 두 디스크의 상대 회전과 비례하며 자석의 어떤 회전과도 무관할 것이다.

반환 경로가 없는 구성

패러데이 디스크는 또한 갈바노미터나 리턴 경로로도 작동할 수 없다. 디스크가 회전하면 전자는 림을 따라 모여 축(또는 반대쪽) 근처에 결손을 남긴다. 예를 들어 림과 차축 사이에 발생하는 기전력을 통해(필수적으로 쉬운 것은 아니지만) 전하의 분포를 측정하는 것이 원칙적으로 가능하다. 이 전하 분리는 디스크와 자석 사이의 상대 회전 속도에 비례한다.

패러데이의 유도 법칙이 0이 아닌 EMF를 예측하는 것처럼 보이지만 실제로는 0이 되는 EMF를 예측하는 역설

이러한 역설은 일반적으로 회로의 외관상 움직임이 실제로 회로의 탈구축에 이어 다른 경로에 있는 회로의 재구성이라는 것을 결정함으로써 해결된다.

추가 규칙

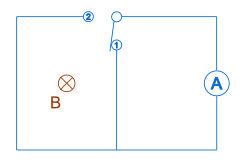
그러나 원반만으로 회선을 통과하는 플럭스의 변화가 없는 경우에는 패러데이의 법칙에 반하여 유도된 기전력이 있다. 플럭스의 변화가 있지만 유도 전압은 없을 때의 예도 보여줄 수 있다. 그림 5(오른쪽 근처)는 틸리의 실험에 사용된 설정을 나타낸다.^[13] 그것은 두 개의 루프나 메쉬가 있는 회로다. 우측 루프에는 갈바노미터, 좌측 루프 중앙에는 자석, 좌측 루프에는 스위치, 루프 사이의 스위치가 연결되어 있다. 우리는 왼쪽의 스위치를 열고 오른쪽의 스위치를 닫는 것부터 시작한다. 좌측의 스위치를 닫고 우측의 스위치를 열면 자석의 장에는 변화가 없지만, 아연도계 회로 영역에는 변화가 있다. 이것은 유동성에 변화가 있다는 것을 의미한다. 그러나 갈바노미터는 유도 전압이 없다는 뜻을 비껴가지 않았으며, 패러데이의 법칙은 이 경우 통하지 않는다. A. G. Kelly에 따르면 이는 패러데이의 실험에서 유도 전압은 플럭스 라인에 의한 회로의 "절단" 때문이지 "플럭스 링크"나 실제 플럭스 변화에 의한 것이 아니라는 것을 암시한다. 이것은 틸리 실험에서 따르며, 회로에 걸친 힘의 선들의 움직임이 없고, 따라서 회로를 통한 플럭스의 변화는 있지만 유도된 전류가 없기 때문이다. 누스바움은 패러데이의 법칙이 유효하기 위해서는 플럭스의 변화를 생산하는 작업이 이루어져야 한다고 제안한다.^[14]
이 생각을 이해하기 위해 누스바움이 제시한 주장을 밟아 나가겠다.^[14] 우리는 두 전류가 흐르는 전선 사이의 힘을 계산하는 것으로 시작한다. 와이어 2로 인한 와이어 1의 힘은 다음과 같다.

${\displaystyle \mathbf {F} _{21}={\frac {\mu _{0}{4\pi }}}{1}I_{2}\oint _{C_{1}}\oint _{C_{2}}{\frac {d\mathbf {l_{1}} \ \mathbf {\times } \ (d\mathbf {l_{2}} \ \mathbf {\times } \ {\hat {\mathbf {r} }}_{21})}{r_{21}^{2}}}}$

두 번째 와이어에서 나오는 자기장은 다음과 같이 주어진다.

${\displaystyle \mathbf {B} _{2}={\frac {\mu _{0}}{4\pi }}I_{2}\oint _{C_{2}}{\frac {(d\mathbf {l_{2}} \ \mathbf {\times } \ {\hat {\mathbf {r} }}_{21})}{r_{21}^{2}}}}$

그래서 우리는 와이어 1의 힘을 다음과 같이 다시 쓸 수 있다.

${\displaystyle \mathbf {F} _{21}=I_{1}\point _{C_{1}d\mathbf {l_{1} \mathbf {\times } \mathbf {B} _{2}}$

이제 일정한 자기장에서 d$$ ${\displaystyle r\mathbf{}}$ ${\$$displaystyle d\mathbf {l}$ 도체의$$ ${\displaystyle 세그먼트\mathbf{}}$ d {\$displaystyle d\mathbf {r}을($를) 고려하십시오. 수행한 작업은 다음에서 찾을 수 있다.

${\displaystyle dW=d\mathbf {F} \cdot d\mathbf {r}$

이전에 $찾은{\displaystyle }$ d ${\displaystyle F\mathbf{}}$ ${\$에 대한 플러그를 꽂으면 다음$$ 정보를 얻을 수 있다.

${\displaystyle dW=(Id\mathbf {l} \mathbf {\times } \mathbf {B} )\cdot d\mathbf {r}}$

도체의 변위가 적용되는 영역은 다음과 같다.

$\d\mathbf {S} =d\mathbf {r} \mathbf {r} \mathbf {\times }d\mathbf {l}}$

따라서 다음과 같다.

${\displaystyle dW=I\mathbf {B} \cdot d\mathbf {S} =Id\Phi _{B}}$

차등 작업은 충전 $d{\displaystyle }$ ${\displaystyle q}$ ${\displaystyle dq}$ 및$$ $잠재적{\displaystyle }$ 차이 V ${\displaystyle$ V$\}:$

${\displaystyle dW=Vdq=VIdt}$

차등 작업에 대한 두 방정식을 서로 동등하게 설정함으로써 우리는 패러데이의 법칙에 도달한다.

${\displaystyle d\Phi _{B}=Vdt}$

더욱이, 이제 우리는 $d{\displaystyle }$ ${\displaystyle W}$ ${\displaystyle dW}$이(가) 비바니싱인 경우에만 해당된다는 것을 알게 되었다. 즉, 패러데이의 법칙은 플럭스의 변화를 가져오는 작업이 수행되어야만 유효하다.

이러한 상황에서 패러데이의 법칙을 검증하는 수학적 방법은 패러데이의 유도 법칙의 증명에서와 같이 EMF의 정의를 일반화하는 것이다.

${\displaystyle \mathrm {EMF} =\point \left(\mathbf {E} +\mathbf {v} \time \mathbf {B} \right)\cdot d{\boldsymbol {\\ell}}}}$

전류를 회로에 기여하는 EMF의 첫 번째 용어만 측정하지만, 때로는 전류를 운동 전자파 측정기로 측정하는 전류의 일부에 기여하는 두 번째 기간(예: 패러데이 디스크 실험)과 같은 두 번째 기간의 통합을 측정할 수 있다. 위의 상황에서는 첫 번째 항이 0이고 첫 번째 항만 전류가 측정되는 전류를 유도하므로 유도 전압이 없다. 단, 위의 EMF 일반화에서 자속의 명백한 변화는 2기로 가기 때문에 패러데이의 법칙은 여전히 유효하다. 그러나 그것은 갈바노미터에 의해 측정되지 않는다. $v{\displaystyle \mathbf{}}$ ${\$}은(는) 충전 캐리어가 아니라 회로에 있는 점의 로컬 속도라는$$ 점을 기억하십시오. 결국, 이 모든 상황은 물질의 상대성 및 미세구조, 그리고/또는 맥스웰 방정식과 로렌츠 공식의 완전성 또는 이들의 조합인 해밀턴 역학과 일치한다.

참고 항목

• 패러데이의 유도 법칙
• 로렌츠 힘
• 이동 자석 및 도체 문제
• 코로팅 전기장

참조

추가 읽기

• Michael Faraday, 전기 실험 연구, Vol I, First Series, 1831년 서구의 위대한 책들, Vol 45, R. M. Hutchins, edd, Edddia Britannica, Inc., 1952년 시카고 대학. [1]
• Giuseppe Giuliani의 "전자기 유도: 물리학과 플래시백"(PDF) – 패러데이 디스크의 로렌츠 힘에 대한 세부 정보
• "Homopolar Electric Dynamo" – 패러데이 디스크의 EMF에 대한 방정식의 파생 포함
• Don Lancaster의 "Tech Musings" 칼럼, 1998년 2월 - 패러데이 디스크의 실제 비효율성에 관한 내용
• "파라데이의 마지막 수수께끼; 필드가 자석을 가지고 회전하는가?" (PDF) – 반론적 이론이지만, 패러데이의 실험에 대한 유용한 언급이 포함되어 있다.
• P. J. Scanlon, R. N. Henricsen, J. R. Allen, "전자 유도 승인", Am. J. Phys. 37, 698–708(1969). – 패러데이의 디스크에 패러데이의 법칙을 적용하는 방법 설명
• 호르헤 구알라-발베르데, 페드로 마조니, 리카르도 아킬레스 "호모폴라 모터: 진정한 상대론적 엔진," Am. J. Phys. 70 (10), 1052–1055 (2002년 10월). – 로렌츠 힘만이 패러데이의 디스크를 설명할 수 있으며 이에 대한 일부 실험 증거를 설명할 수 있다고 주장한다.
• Frank Munley, Faraday의 플럭스 룰에 도전, Am. J. Phys. 72, 1478 (2004) – 위의 Scanlon 참조에서 개념에 대한 최신 토론.
• 리처드 파인만, 로버트 레이튼, 매튜 샌즈, "페인만의 물리학 제2권 강의", 제17장 – 패러데이 "파라독스"(연결 플럭스는 변하지 않지만 emf는 유도되는 경우) 외에도, 그는 연결된 플럭스는 변화하지만 emf는 유도되지 않는 "로킹 플레이트" 실험을 설명한다. 그는 로렌츠 힘과 맥스웰-파라데이 방정식의 조합(견적 상자 참조)에 의해 항상 올바른 물리학이 주어지는 것을 보여주며, 이 두 가지 자신의 "파라독스"를 포즈한다.
• Vanja Janezic에 의한 자기장의 회전 – 누구나 할 수 있는 간단한 실험을 설명한다. 두 개의 몸만 포함하기 때문에 3체 패러데이, 켈리, 구알라-발베르데 실험에 비해 결과가 덜 모호하다.
• W. F. Hughes와 F. J. Young, The Electrogenodynamics of Fluids, John Wiley & Sons (1965) LCCC #66-17631. 1장. 특수상대성의 원칙과 2 무빙 미디어의 전기역학. 이 장들에서 유도된 모든 emf 문제를 다루고 문헌에서 발견되는 모든 관련 역설을 설명할 수 있다.