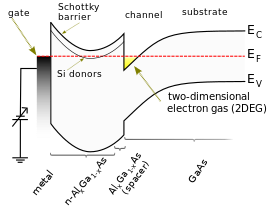
페르미 준위

고체 물체의 페르미 수준은 물체에 하나의 전자를 추가하는 데 필요한 열역학 작업입니다.이것은 열역학적 양으로 일반적으로 간결함을 나타내는 δ 또는_F^[1] E로 표시됩니다.페르미 레벨은 전자가 어디에서 오든 전자를 제거하는 데 필요한 작업을 포함하지 않습니다.페르미 수준을 정확하게 이해하는 것은 고체물리학을 이해하는 데 필수적입니다. 즉, 페르미 수준이 전자특성을 결정할 때 전자밴드 구조와 어떻게 관련되어 있는지, 전자회로의 전압 및 전하 흐름과 어떻게 관련되어 있는지를 이해하는 데 필수적입니다.

고체의 에너지 레벨을 분석하기 위해 고체 물리학에서 사용되는 밴드 구조 이론에서, 페르미 레벨은 전자의 가정적인 에너지 레벨로 간주될 수 있으며, 열역학 평형에서 이 에너지 레벨이 ^{[clarification needed]}주어진 시간에 점유될 확률이 50%일 것입니다.밴드 에너지 레벨에 대한 페르미 레벨의 위치는 전기적 특성을 결정하는 데 중요한 요소입니다.페르미 레벨은 실제 에너지 레벨과 반드시 일치하는 것은 아니며(절연체에서는 페르미 레벨이 밴드 갭에 있다), 밴드 구조의 존재도 필요하지 않습니다.그럼에도 불구하고 페르미 레벨은 정확하게 정의된 열역학적 양이며, 페르미 레벨의 차이는 단순히 전압계로 측정할 수 있다.

전압 측정

전류는 정전위(갈바니 전위)의 차이에 의해 구동된다고 하는 경우도 있습니다만,^[2] 이것은 정확하게 사실이 아닙니다.반례로 p-n 접합과 같은 복합 재료 장치는 평형 상태에서 내부 정전 전위차를 포함하지만 그에 따른 순 전류는 없다. 전압계를 접합부에 연결하면 ^[3]0V만 측정할 수 있다.분명히 정전기 전위가 재료의 전하 흐름에 영향을 미치는 유일한 요인은 아닙니다. Pauli 반발, 반송파 농도 경사, 전자파 유도 및 열 효과도 중요한 역할을 합니다.

실제로 전자회로로 측정된 전압이라 불리는 양은 전자에 대한 화학적 잠재력(페르미 수준)과 단순한 관계가 있습니다.전압계의 리드가 회로의 두 지점에 연결되어 있는 경우 표시되는 전압은 단위 전하가 한 지점에서 다른 지점으로 이동할 수 있을 때 전달되는 총 작업량의 측정값입니다.전압이 다른 두 지점 사이에 간단한 와이어가 연결되어 있는 경우(단락 회로 형성), 전류가 양전압에서 음전압으로 흐르면서 사용 가능한 작업을 열로 변환합니다.

물체의 페르미 수준은 물체에 전자를 추가하는 데 필요한 작업 또는 전자를 제거함으로써 얻은 작업을 동일하게 나타냅니다.따라서 전자회로의_B 두 점 A와 B 사이의 전압차 V - V는 다음_A 식에^[4] 따라 페르미 준위의 화학전위차 δ_A - δ와_B 정확히 관련된다.

여기서 -e는 전자 전하입니다.

위의 설명에서 단순한 경로가 제공되면 전자가 높은 δ(저전압)에서 낮은 δ(고전압)로 이동하는 것을 알 수 있습니다.이러한 전자의 흐름은 낮은 δ를 증가시키고(충전 또는 다른 반발 효과로 인해) 마찬가지로 높은 δ를 감소시킵니다.결국 will는 양쪽에서 같은 값으로 안정된다.이는 전자회로의 평형(OFF) 상태에 관한 중요한 사실로 이어집니다.

이는 평형 상태에서 두 지점 사이의 전압(전압계로 측정)이 0이 된다는 의미이기도 합니다.여기서의 열역학적 평형에서는 회로가 내부적으로 연결되어 있고 배터리나 다른 전원 또는 온도 변화가 없어야 합니다.

고체의 밴드 구조

고체의 띠 이론에서 전자는 각각 θ로 표시된 단일 입자 에너지 고유 상태로 구성된 일련의 띠를 차지하는 것으로 간주된다.이 단일 입자 그림은 근사치이지만, 전자 거동에 대한 이해를 크게 단순화하고 일반적으로 올바르게 적용했을 때 정확한 결과를 제공합니다.

페르미-디락 분포 $)$ {$displaystyle$ f$(\epsilon$는 (열역학적 평형 상태에서) 에너지가 ^[5]θ인 상태가 전자에 의해 점유될 가능성을 제공한다.

여기서 T는 절대 온도이고 k는_B 볼츠만의 상수이다.페르미 레벨의 상태(θ = θ)가 있으면 이 상태가 점유될 확률이 50%가 됩니다.분포는 왼쪽 그림에 표시되어 있습니다.f가 1에 가까울수록 이 상태가 점유될 가능성이 높아집니다.f가 0에 가까울수록 이 상태가 비어 있을 가능성이 높아집니다.

소재의 밴드 구조 내에서 δ의 위치는 소재의 전기적 거동을 결정하는 데 중요하다.

• 절연체에서 θ는 큰 밴드갭 내에 존재하며 전류를 통전할 수 있는 어떤 상태에서도 멀리 떨어져 있습니다.
• 금속, 세미메탈 또는 축퇴 반도체에서 δ는 비국재 대역 내에 있다.δ 근방의 많은 상태는 열활성이며 쉽게 전류를 흐른다.
• 본 발명의 도프형 반도체에서 δ는 밴드 에지에 충분히 가깝고, 그 밴드 에지 근방에 희박한 수의 열여진 캐리어가 존재한다.

반도체 및 세미메탈에서 밴드 구조에 대한 δ의 위치는 보통 도핑 또는 게이트에 의해 유의하게 제어될 수 있다.이러한 컨트롤은 전극에 의해 고정되는 which를 변경하는 것이 아니라 밴드 구조 전체를 상하로 이동시킨다(밴드 구조의 형태를 바꾸는 경우도 있다).반도체의 페르미 수준에 대한 자세한 내용은 (예:) ^[6]Sze를 참조하십시오.

국소전도대역기준, 내부화학전위 및 파라미터 »

기호 θ가 주변 밴드 θ의_C 가장자리에 있는 에너지와 비교하여 측정된 전자 에너지 수준을 나타내기 위해 사용되는 경우 일반적으로 θ = θ – θ가_C 있습니다.밴드 에지를 기준으로 페르미 레벨을 참조하는 파라미터 θ를^[7] 정의할 수 있습니다.

따라서 페르미-디락 분포 함수는 다음과 같이 쓸 수 있다.

금속의 띠 이론은 1927년부터 소머펠트에 의해 처음 개발되었으며, 소머펠트는 기초 열역학 및 통계역학에 많은 관심을 기울였습니다.혼란스럽지만, 어떤 상황에서는 대역 기준량 θ를 페르미 수준, 화학 퍼텐셜 또는 전기 화학 퍼텐셜이라고 부를 수 있으며, 이로 인해 전지구 기준 페르미 수준과의 모호성이 초래된다.본 기사에서는 전도대역 기준 페르미 수준 또는 내부 화학 퍼텐셜이라는 용어가 ζ를 가리키는 데 사용된다.

δ는 활성 전하 운반체의 수와 그들의 전형적인 운동 에너지와 직접적으로 관련이 있으며, 따라서 물질의 국부적 특성(예: 전기 전도성)을 결정하는 데 직접적으로 관여한다.이러한 이유로 단일 균질 전도성 물질에서 전자의 특성에 집중할 때 δ의 값에 초점을 맞추는 것이 일반적입니다.자유전자의 에너지 상태에 비유하면, 상태의 δ는 그 상태의 운동 에너지이고, δ는_C 그 위치 에너지이다.이를 염두에 두고 매개변수 δ는 페르미 운동 에너지로 표기될 수도 있다.

,과 달리 파라미터 ,은 평형상태에서 상수가 아니라 소재의_C 품질, 불순물/도판트 등의 요인에 의해 결정되는 ,의 변화에 따라 소재 내 위치마다 다르다.반도체 또는 세미메탈 표면 근방에서는 전계효과 트랜지스터와 같이 외부적으로 인가되는 전계에 의해 δ를 강하게 제어할 수 있다.멀티밴드 재료에서는 θ가 한 장소에서 여러 값을 가질 수도 있습니다.예를 들어 알루미늄 금속 조각에는 페르미 레벨을 가로지르는 두 개의 전도 밴드가 있습니다(다른 ^[8]재료에서는 더 많은 밴드). 각 밴드에는 서로 다른 에지 에너지인 δ와_C 서로 다른 δ가 있습니다.

0 온도에서 θ의 값은 페르미 에너지로 널리 알려져 있으며, 때로는 θ로₀ 표기되기도 한다.혼란스럽지만 페르미 에너지라는 이름은 때때로 0이 아닌 온도에서 δ를 가리키는 데 사용됩니다.

온도가 평형을 벗어남

페르미 레벨 μ 및 온도 T는 열역학적 평형 상황(예: 선반에 아무것도 하지 않는 경우)에서 고체 소자에 대해 잘 정의된 상수입니다.장치가 평형을 벗어나 사용되면 페르미 수준과 온도는 더 이상 잘 정의되지 않습니다.다행히도, 열 분포의 관점에서 상태 점령을 정확하게 설명하는 특정 위치에 대한 준페르미 수준과 준온도를 정의할 수 있는 경우가 많다.이러한 설명이 가능한 경우, 디바이스는 준균형 상태에 있다고 한다.

준균형 접근방식을 사용하면 금속 조각의 전기 전도율(μ의 경사도 결과) 또는 열 전도율(T의 경사도 결과)과 같은 일부 비균형 효과에 대한 간단한 그림을 작성할 수 있습니다.준μ 및 준T는 다음과 같은 비균형 상황에서 변화할 수 있다(또는 전혀 존재하지 않는다).

• 시스템에 화학적 불균형이 있는 경우(배터리 등).
• 시스템이 변화하는 전자장에 노출되는 경우(콘덴서, 인덕터 및 변압기 등).
• 태양과 같이 온도가 다른 광원의 조명 아래(태양전지 등)
• 장치 내 온도가 일정하지 않은 경우(열전대 등),
• 장치가 변경되었지만 재조정할 시간이 충분하지 않은 경우(압전 또는 초전 물질 등).

물질이 고에너지 레이저 펄스를 경험한 직후와 같은 일부 상황에서는 전자 분포를 열 분포로 설명할 수 없습니다.이 경우 준페르미 수준이나 준온도를 정의할 수 없다.전자는 단순히 비열화라고 한다.일정한 조명 아래 태양 전지와 같이 덜 극적인 상황에서는 준균형 묘사가 가능하지만 다른 대역(접속 대역 대 원자가 대역)에 μ와 T의 개별 값을 할당해야 한다.이 경우에도 전류가 구동될 때 μ 및 T의 값은 재료 계면(예를 들어 p-n 접합부)을 통해 불연속적으로 점프하여 계면 자체에서 잘못 정의될 수 있다.

테크니컬리티

용어 문제

페르미 레벨이라는 용어는 반도체에서 전자의 고체물리학을 논할 때 주로 사용되며, 도핑 레벨이 다른 다른 물질로 구성된 소자에서의 밴드 다이어그램을 기술하기 위해서는 이 용어의 정확한 사용이 필요하다.그러나 이러한 맥락에서, 위의 θ라고 불리는 밴드 기준 페르미 레벨 θ - θ를_C 참조하기 위해 부정확하게 사용되는 페르미 레벨을 볼 수도 있다.과학자와 엔지니어는 도핑이나 전계효과로 인한 δ의_C 변화를 실제로 설명할 때 도체 내부의 페르미 레벨을 "제어", "핀잉" 또는 "조정"하는 것을 흔히 볼 수 있다.사실, 열역학 평형은 도체의 페르미 레벨이 항상 전극의 페르미 레벨과 정확히 같도록 고정되어 있음을 보증합니다. 도핑이나 전계 효과에 의해 밴드 구조(페르미 레벨이 아님)만 변경될 수 있습니다(밴드 다이어그램 참조).화학 퍼텐셜과 전기 화학적 퍼텐셜 사이에는 유사한 모호성이 존재한다.

페르미 레벨이 페르미 에너지와 반드시 같은 것은 아니라는 점도 중요합니다.양자역학에서 페르미 에너지라는 용어는 일반적으로 이상적인 비상호작용, 무질서, 제로 온도 페르미 기체에서 페르미온의 최대 운동 에너지를 가리킨다.이 개념은 매우 이론적이다(비상호작용 페르미 가스 같은 것은 없으며, 0 온도를 달성하는 것은 불가능하다).하지만, 그것은 백색왜성, 중성자별, 원자핵, 그리고 금속의 전자를 대략적으로 묘사하는 데 어느 정도 쓰입니다.한편, 반도체 물리나 공학 분야에서는, 이 ^[9]기사에 기재된 페르미 레벨을 나타내는 데 페르미 에너지가 자주 사용되고 있다.

페르미 레벨 참조 및 0 페르미 레벨의 위치

좌표계의 원점 선택과 마찬가지로 에너지의 영점은 임의로 정의할 수 있습니다.관측 가능한 현상은 에너지 차이에만 의존합니다.그러나 별개의 물체를 비교할 때, 에너지 0의 위치를 선택하는 데 있어 모두 일관성이 있어야 한다. 그렇지 않으면 터무니없는 결과를 얻을 수 있다.따라서 공통점을 명시적으로 지정하여 서로 다른 구성요소가 일치하는지 확인하는 것이 도움이 될 수 있습니다.한편, 기준점이 본질적으로 애매한 경우("진공"과 같이, 아래 참조) 더 많은 문제가 발생합니다.

실용적이고 타당한 공통점은 전기 접지 또는 접지와 같은 부피가 큰 물리적 도체입니다.이러한 도체는 양호한 열역학적 평형 상태에 있다고 간주할 수 있으므로 그 θ는 잘 정의된다.충전 효과를 일으키지 않고 많은 전자를 추가하거나 제거할 수 있도록 전하 저장고를 제공합니다.또, 다른 물체의 페르미 레벨도 간단하게 전압계로 측정할 수 있도록, 액세스 할 수 있는 장점도 있습니다.

"진공 중의 에너지"를 기준 0으로 사용하지 않는 이유

원칙적으로 진공 중의 정지 전자 상태를 에너지의 기준점으로 사용하는 것을 고려할 수 있다.진공이 정확히 어디에 ^[10]있는지 신중하게 정의하지 않는 한 이 방법은 권장되지 않습니다.문제는 진공의 모든 점이 동일하지 않다는 것입니다.

열역학적 평형에서는 1V 차수의 전위차가 진공(Volta 전위)에 존재하는 것이 일반적입니다.이러한 진공 전위 변동의 원인은 진공에 노출된 서로 다른 전도 재료 간의 작업 기능의 변동입니다.도체 바로 밖에서 정전 전위는 재료와 선택된 표면(결정 방향, 오염 및 기타 세부 사항)에 따라 민감하게 달라집니다.

보편성에 가장 적합한 근사치를 제공하는 매개변수는 위에서 제안한 지구 기준 페르미 수준입니다.또한 전압계로 측정할 수 있다는 이점도 있습니다.

소규모 시스템의 개별 충전 효과

단일 전자에 의한 "충전 효과"가 무시할 수 없는 경우 위의 정의를 명확히 해야 한다.예를 들어, 2개의 동일한 병렬 플레이트로 이루어진 콘덴서를 생각해 보겠습니다.콘덴서가 충전되지 않은 경우, 페르미 레벨은 양쪽에서 동일하기 때문에 한 판에서 다른 판으로 전자를 이동시키는 데 에너지가 필요하지 않다고 생각할 수 있습니다.그러나 전자가 이동하면 캐패시터가 (약하게) 충전되므로 약간의 에너지가 필요합니다.일반 캐패시터에서는 무시할 수 있지만 나노 스케일 캐패시터에서는 더 중요할 수 있습니다.

이 경우 화학적 전위의 열역학적 정의와 장치 상태에 대해 정확하게 설명해야 합니다. 즉, 전기적으로 절연된 상태입니까, 아니면 전극에 연결된 상태입니까?

• 신체가 전극(저장고)과 전자와 에너지를 교환할 수 있을 때, 그것은 그랜드 표준 앙상블에 의해 설명된다.화학전위θ의 값은 전극에 의해 고정된다고 할 수 있으며, 체내 전자수 N은 변동할 수 있다.이 경우, 물체의 화학적 잠재력은 평균 전자 수를 극소량만큼 증가시키는 데 필요한 극소량의 작업량이다(항상 전자 수가 정수일지라도, 평균 수는 지속적으로 변화한다).:
  $$\displaystyle \mu(\left\right\rangle, T)=\left(\frac {\frac {\partial \left\right\rangle }}\right)_{T}$$

  
  여기서 F(N, T)는 그랜드 표준 앙상블의 자유 에너지 함수이다.
• 체내의 전자수가 고정되어 있는 경우(그러나 몸은 여전히 열욕에 열적으로 연결되어 있는 경우), 정준 앙상블에 있습니다.이 경우 '화학적 잠재력'을 문자 그대로 N개의 ^[11]전자를 가진 물체에 1개의 전자를 추가하는 데 필요한 작업이라고 정의할 수 있습니다.
  $$(\displaystyle \mu '(N,T)=F(N+1,T)-F(N,T),}$$

  
  여기서 F(N, T)는 표준 앙상블의 자유 에너지 함수이다.
  $$\displaystyle \mu '(N,T)=F(N,T)-F(N-1,T)=\mu '(N-1,T)}$$

  

이러한 화학적 전위는 열역학 한계를 제외하고 등가하지 않습니다.이 구별은 ^[12]쿨롱 봉쇄를 보여주는 것과 같은 작은 시스템에서 중요합니다.파라미터 δ(전자 수가 변동할 수 있는 경우)는 소규모 시스템에서도 전압계 전압과 정확히 관련된 상태로 유지됩니다.정확히 말하면 페르미 레벨은 하나의 전자 전하에 의한 결정론적 충전 이벤트에 의해서가 아니라, 전자의 극소수에 의한 통계적 충전 이벤트에 의해서 정의된다.

각주 및 참고 자료