업무기능

고체물리학에서 일함수(일함수라고도 함)는 고체에서 고체 표면 바로 바깥의 진공점까지 전자를 제거하기 위해 필요한 최소 열역학적인 일(에너지)이다.여기서 "즉시"는 최종 전자 위치가 원자 눈금의 표면에서 멀리 떨어져 있지만 진공 내 주변 전계의 영향을 받기에는 여전히 고체에 너무 가깝다는 것을 의미한다.작업 기능은 벌크 재료의 특성이 아니라 재료 표면의 특성입니다(결정 표면 및 오염에 따라 다름).

정의.

주어진 표면에 대한 작업 $함수$ W는 다음 차이에^[1] 의해 정의된다.

W=-e\phi -E_{\rm {F}

$여기$ 서 -e는 전자의 전하, $θ$ 는 표면 근처의 진공에서의 정전위, $E$ 는_F 물질 내부의 페르미 수준(전자의 전기화학 퍼텐셜)이다.용어 $-eθ$ 는 표면 근처의 진공에서 정지해 있는 전자의 에너지입니다.

금-진공-알루미늄 시스템의 위치에 대한 전자 에너지 수준의 그림입니다.여기에 묘사된 두 금속은 완전한 열역학적 평형 상태에 있다.단, 작업함수의 차이로 인해 진공정전위θ는 평탄하지 않다.

실제로 전극을 통해 재료에 인가되는 전압에 의해 E를 직접 $제어$ 하며_F, 일반적으로 작업함수는 표면재료의 고정특성이다.따라서 재료에 전압을 인가할 때 진공에서 발생하는 $정전위θ$ 가 재료 표면의 작업함수에 따른 인가전압보다 다소 낮아지는 것을 의미한다.위의 방정식을 재정렬하면 다음과 같이 된다.

\displaystyle \phi = V-{\frac {W}{e}}

$여기$ 서 V = $-E F / e$ 는 페르미 레벨이 0인 것으로 정의된 전기 접지에 대한 (전압계로, 부착된 전극을 통해 측정한) 물질의 전압이다. $δ$ 가 재료 표면에 의존한다는 것은 두 개의 다른 도체 사이의 공간이 서로 완전한 평형 상태일 때(전기적으로 서로 단락되고 온도가 동일할 때) 내장 전계를 갖는다는 것을 의미한다.

작업 기능은 표면에서 충분히 떨어진 위치(많은 nm)에서 전자를 제거하는 것으로, 표면에서 전자와 그 상전하 사이의 ^[1]힘이 무시될 수 있습니다.또한 전자는 결정면의 가장 가까운 가장자리 또는 재료 조성, 표면 코팅 또는 재구성 등의 표면 구조의 다른 변화와 비교하여 표면에 가까워야 한다.이러한 구조에서 발생하는 내장 전계 및 진공에 존재하는 다른 주변 전계는 작업 ^[2]기능을 정의하는 데 제외됩니다.

적용들

열전자 방출: 열전자총에서 열음극의 작업함수와 온도는 방출 가능한 전류의 양을 결정하는 데 중요한 매개 변수입니다.진공관 필라멘트의 일반적인 선택인 텅스텐은 고온에서도 견딜 수 있지만 상대적으로 높은 작업 기능(약 4.5eV)으로 인해 배출량이 다소 제한됩니다.텅스텐에 작업기능이 낮은 물질(예를 들어 토륨이나 산화바륨)을 도포함으로써 방출량을 크게 높일 수 있다.이는 낮은 온도에서 작동할 수 있게 함으로써 필라멘트의 수명을 연장시킵니다(자세한 내용은 핫 캐소드 참조).
솔리드 스테이트 전자 장치의 밴드 벤딩 모델: 솔리드 스테이트 디바이스의 동작은 금속, 반도체 및 절연체와 같은 다양한 재료의 접합부에 있는 다양한 쇼트키 장벽 및 밴드 오프셋의 크기에 크게 좌우됩니다.앤더슨 법칙과 쇼트키-모트 법칙과 같이 재료 사이의 밴드 정렬을 예측하기 위해 일반적으로 사용되는 몇몇 발견적 접근법은 표면이 접촉하기 직전에 충전되고 그들의 작업 기능이 같아지도록 진공 상태에서 함께 오는 두 재료의 사고 실험에 기초한다.실제로 이러한 작업 기능 휴리스틱은 수많은 현미경 효과를 무시하기 때문에 부정확하다.그러나 실제 ^[3]^[4]값을 실험을 통해 확인할 수 있을 때까지 편리한 추정치를 제공합니다.
진공 챔버 내 평형 전계: 서로 다른 표면 간의 작업 기능의 변화는 진공에서 불균일한 정전 전위를 발생시킵니다.표면적으로 균일한 표면에서도 패치 퍼텐셜로 알려진 W의 $변화$ 는 항상 존재하며, 이는 미세한 불균형으로 인해 발생합니다.패치 전위는 카시미르 힘 실험이나^[5] 중력 프로브 B ^[6]실험과 같이 완전히 균일한 진공에 의존하는 민감한 장치를 교란시켰습니다.중요한 장치는 몰리브덴으로 덮인 표면을 가질 수 있으며, 이는 서로 다른 결정면 ^[7]간의 작업 기능 편차가 낮음을 보여준다.
접점 전화: 두 개의 도전 표면이 서로 상대적으로 이동하며 그 사이의 공간에 전위차가 있으면 전류가 구동됩니다.이는 도체의 표면 전하가 전기장의 크기에 따라 달라지고, 이는 표면 간의 거리에 따라 달라지기 때문입니다.외부에서 관찰되는 전기적 효과는 도체가 접촉하지 않고 가장 작은 거리만큼 떨어져 있을 때 가장 큽니다(일단 접촉하면 대신 전하가 도체 사이의 접합부를 통해 내부적으로 흐릅니다).평형 상태에 있는 두 도체는 작업 기능 차이로 인해 전위차가 내장될 수 있기 때문에 이종 도체를 접촉시키거나 분리하여 전류를 구동할 수 있습니다.이러한 접촉 전류는 민감한 마이크로 전자 회로를 손상시킬 수 있으며,^[8] 움직임이 없을 때 컨덕터가 접지된 경우에도 발생합니다.

측정.

특정 물리적 현상은 작업 기능의 값에 매우 민감합니다.이러한 효과에서 관측된 데이터를 단순화된 이론 모형에 적합시킬 수 있으므로 작업 함수의 값을 추출할 수 있습니다.이러한 현상학적으로 추출된 작업 함수는 위에서 설명한 열역학적 정의와 약간 다를 수 있습니다.불균일한 표면의 경우, 작업 함수는 장소마다 다르며, 방법마다 현미경 작업 함수 ^[9]간에 평균화 또는 선택 방식이 다르기 때문에 일반적인 "작업 함수"의 다른 값을 산출한다.

샘플의 전자 작업 기능을 측정하기 위해 다양한 물리적 효과를 기반으로 많은 기술이 개발되었습니다.작업 기능 측정에 대한 두 가지 실험 방법 그룹, 즉 절대 및 상대 그룹을 구별할 수 있습니다.

절대 방법은 광자 흡수(광전자 방출), 고온(열전자 방출), 전계(전계 전자 방출) 또는 전자 터널링에 의해 유도되는 샘플로부터의 전자 방출을 사용한다.
상대적인 방법은 샘플과 기준 전극 사이의 접촉 전위차를 이용한다.실험적으로 다이오드의 양극전류를 이용하거나 샘플과 기준 사이의 정전용량의 인위적인 변화에 의해 생성되는 변위전류를 측정한다(켈빈프로브법, 켈빈프로브력현미경).그러나 팁이 먼저 기준 ^[10]샘플에 대해 보정된 경우 절대 작업 함수 값을 얻을 수 있습니다.

열전자 방출에 기초한 방법

열변동이 뜨거운 물질('에미터'라고 함)에서 진공으로 전자를 "증발"하기에 충분한 에너지를 제공하는 열전자 방출 이론에서 작업 기능은 중요합니다.이러한 전자가 다른 차가운 물질(컬렉터라고 함)에 흡수되면 측정 가능한 전류가 관찰됩니다.열전자 방출을 사용하여 핫 이미터와 콜드 콜렉터의 작업 기능을 측정할 수 있습니다.일반적으로 이러한 측정은 리처드슨의 법칙에 적합해야 하므로 공간 전하 효과가 없는 저온 및 저전류 상태에서 수행해야 합니다.

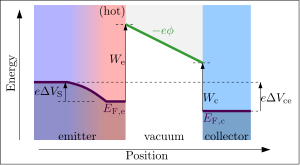
전방 바이어스 구성의 열전자 다이오드에 대한 에너지 레벨 다이어그램. 이미터의 표면에서 나오는 모든 뜨거운 전자를 추출하는 데 사용됩니다.장벽은 이미터 표면 근처의 진공입니다.

뜨거운 이미터에서 진공으로 이동하기 위해서는 전자의 에너지가 이미터 페르미 수준을 어느 정도 초과해야 한다.

\displaystyle E_{\rm {display}}=W_{\rm {e}}}

단순히 이미터의 열전자 작용 기능에 의해 결정된다.전계가 이미터의 표면에 인가되면 모든 탈출 전자가 이미터에서 가속되어 전계를 인가하는 물질에 흡수됩니다.리처드슨의 법칙에 따르면 방출 전류 밀도(이미터의 단위 면적당) J_e(A/m²)는 다음 방정식으로 이미터의 절대 온도_e T와 관련이 있습니다.

{\displaystyle J_{\rm {e}}=-A_{\rm {e}}T_{\rm {e}}^{2}e^{-E_{\rm {barrier}}/kT_{\rm {e}}}}:

여기서 k는 볼츠만 상수이고, 비례_e 상수 A는 이미터에 대한 리차드슨의 상수입니다.이 경우 T에 대한_e J의 의존성을_e W로_e 적합시킬 수 있습니다.

콜드 일렉트론 컬렉터의 작업 기능

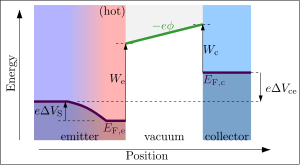
지연 전위 구성의 열전자 다이오드에 대한 에너지 레벨도.장벽은 집진기 근처의 진공 표면입니다.

인가 전압을 조정하는 것만으로 집전기의 작업 기능을 측정할 수 있습니다.대신 이미터에서 떨어진 곳에 전계가 인가되면 이미터에서 나오는 대부분의 전자는 이미터로 반사됩니다.가장 높은 에너지 전자만이 집전기에 도달하기에 충분한 에너지를 가지며, 이 경우 전위 장벽의 높이는 이미터가 아닌 집전기의 작업 기능에 따라 다릅니다.

물살은 여전히 리처드슨의 법칙에 의해 지배되고 있다.단, 이 경우 장벽 높이는 W에 의존하지_e 않습니다.이제 장벽 높이는 수집기의 작동 기능과 추가 인가 ^[11]전압에 따라 달라집니다.

\displaystyle E_{\rm {display}}=W_{\rm {c}}-e(\Delta V_{\rm {ce}}-\Delta V_{\rm {S}})}:

여기서_c W는 콜렉터의 열전자 작업 함수, δV는_ce 인가된 콜렉터-이미터 전압_S, δV는 핫 이미터의 제벡 전압입니다(차수 10mV의 작은 기여이므로 δV의_S 영향은 종종 생략됩니다).수집기를 통과하는 결과 전류 밀도_c J(수집기 영역 단위당)는 리처드슨의 법칙에 의해 다시 지정됩니다(단, 지금은 제외).

{\displaystyle J_{\rm {c}}}=AT_{\rm {e}}^{2}e^{-E_{\rm {barrier}}/kT_{\rm {e}}}}:

여기서 A는 수집기 재료에 따라 달라지지만 이미터 재료 및 다이오드 형상에 따라 달라지는 Richardson 유형의 상수입니다.이 경우, T에_e 대한 J의_c 의존성 또는_ce δV를 W로 적합시킬 수 있다_c.

이 지연 전위 방법은 작업 기능을 측정하는 가장 간단하고 오래된 방법 중 하나이며, 고온에서 살아남기 위해 측정된 물질(콜렉터)이 필요하지 않기 때문에 유용합니다.

광방사에 근거한 방법

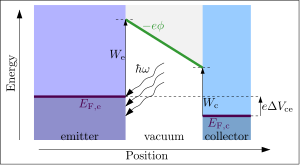
순방향 바이어스 구성의 광전 다이오드. 조명된 이미터의 작업_e 함수 W를 측정하는 데 사용됩니다.

광전 작업 기능은 광전 효과에서 물질로부터 전자를 해방시키는 데 필요한 최소 광자 에너지입니다.광자의 에너지가 물질의 작업 기능보다 크면 광전 방출이 일어나 전자가 표면에서 해방된다.상기 열전자 케이스와 마찬가지로 이미터 표면에 전계가 인가되면 해방된 전자를 집전기로 추출하여 검출 가능한 전류를 발생시킬 수 있다.과도한 광자 에너지는 운동 에너지가 0이 아닌 자유 전자를 발생시킨다.전자 방출(및 전류 생성)에 필요한 최소 광자 에너지 $(\displaystyle\hbar\obega)$ 는 $\hbar \omega$ 다음과 같습니다.

\displaystyle \hbar \mega = W_{\rm {e}}

여기서_e W는 이미터의 작업 함수입니다.

광전 측정은 잘못 설계된 실험 기하학으로 인해 ^[9]작업 기능의 측정이 잘못될 수 있으므로 많은 주의가 필요합니다.이는 과학 문헌에서 업무 함수 값의 큰 변동의 원인이 될 수 있다.게다가 들뜸에 사용할 수 있는 페르미 수준의 실제 전자 상태가 없는 물질에서는 최소 에너지가 오해의 소지가 있습니다.예를 들어, 반도체에서 최소 광자 에너지는 실제로 작업 ^[12]함수보다는 원자가 밴드 단애에 해당된다.

물론 광전효과는 상기 서미온 기기와 마찬가지로 리터치 모드에서도 사용할 수 있다.지각의 경우 대신 다크 콜렉터의 작업함수를 측정한다.

켈빈 프로브법

평면 진공 구성의 켈빈 프로브 에너지 다이어그램. 샘플과 프로브 간의 작업 기능 차이를 측정하는 데 사용됩니다.

Kelvin 프로브 기술은 샘플 재료와 프로브 재료 사이의 전계(θ 단위 경사) 검출에 의존합니다.전계는 시료에 대해 프로브에 인가되는 전압 δV에_sp 따라 변화할 수 있습니다.전계가 제거되도록 전압을 선택한 경우(평탄한 진공 상태),

e\Delta V_{\rm {sp}}}=W_{\rm {s}}-W_{\rm {p}},\quad {text {when}}~\phi~{\text {is flat}}.

실험자가 δV를_sp 제어하고 알기 때문에 평탄한 진공 상태를 찾으면 두 재료 간의 작업 기능 차이를 직접 알 수 있습니다.유일한 질문은, 평평한 진공 상태를 어떻게 감지하느냐는 것입니다.일반적으로 전계는 시료와 프로브 사이의 거리를 변화시킴으로써 검출됩니다.거리가 변경되지만 δV가_sp 일정하게 유지되면 캐패시턴스의 변화로 인해 전류가 흐릅니다.이 전류는 진공 전계에 비례하므로 전계가 중화되면 전류가 흐르지 않습니다.

Kelvin 프로브 기법은 작업 기능의 차이만 측정하지만, 먼저 기준 물질에 대해 프로브를 보정하고(알려진 작업 기능을 사용하여) 동일한 프로브를 사용하여 원하는 ^[10]샘플을 측정함으로써 절대적인 작업 함수를 얻을 수 있습니다.Kelvin 프로브 기술은 프로브에 날카로운 팁을 사용하여 공간 분해능이 매우 높은 표면의 작업 기능 맵을 얻는 데 사용할 수 있습니다(Kelvin 프로브 힘 현미경 참조).

요소의 업무 기능

작업 기능은 재료 표면에 있는 원자의 구성에 따라 달라집니다.예를 들어 다결정 은의 경우 작업 함수는 4.26 eV이지만 은 결정의 경우 (100)면: 4.64 eV, (110)면: 4.52 eV, (111)면: 4.74 ^[13]eV와 같이 결정면에 따라 달라집니다.일반적인 표면의 범위는 ^[14]아래 표에 나와 있습니다.

요소의 작업 기능(eV)

아그	4.26 – 4.74	알	4.06 – 4.26	~하듯이	3.75
오	5.10 – 5.47	B	~4.45	바	2.52 – 2.70
있다	4.98	비	4.31	C	~5
Ca	2.87	CD	4.08	Ce	2.9
회사	5	Cr	4.5	Cs	1.95
CU	4.53 – 5.10	에우	2.5	Fe:	4.67 – 4.81
가	4.32	Gd	2.90	HF	3.90
Hg	4.475	인	4.09	Ir	5.00 – 5.67
K	2.29	라	3.5	리	2.9
루	~3.3	Mg	3.66	Mn	4.1
모	4.36 – 4.95	나	2.36	Nb	3.95 – 4.87
Nd	3.2	니	5.04 – 5.35	OS	5.93
PB	4.25	PD	5.22 – 5.60	Pt	5.12 – 5.93
Rb	2.261	레	4.72	Rh	4.98
루	4.71	Sb	4.55 – 4.70	스케이	3.5
세	5.9	시	4.60 – 4.85	Sm	2.7
스니	4.42	시르	~2.59	타	4.00 – 4.80
Tb	3.00	테	4.95	Th(Th)	3.4
티	4.33	Tl	~3.84	U	3.63 – 3.90
V	4.3	W	4.32 – 5.22	Y	3.1
YB	2.60^[15]	Zn	3.63 – 4.9	Zr	4.05

업무 기능을 결정하는 물리적 요인

아래 모델링 섹션에서 설명하는 복잡성 때문에 이론적으로 작업 기능을 정확하게 예측하는 것은 어렵습니다.그러나 다양한 추세가 확인되고 있다.작업 함수는 열린 ^{[clarification needed]}격자를 가진 금속의 경우 더 작고 원자가 촘촘히 채워진 금속의 경우 더 큰 경향이 있습니다.열린 결정면보다 밀도가 높은 결정면에서 다소 높으며, 주어진 결정면에 대한 표면 재구성에 따라 다릅니다.

표면 쌍극자

표면에서 ^[7]원자 규모의 전기 이중층이 형성되기 때문에 작업 기능은 단순히 재료 내부의 "내부 진공 수준"(즉, 평균 정전위)에 의존하지 않는다.이 표면 전기 쌍극자는 물질과 진공 사이의 정전위 점프를 제공합니다.

표면 전기 쌍극자에는 다양한 요인이 작용합니다.표면이 완전히 깨끗하더라도 전자는 진공으로 약간 퍼질 수 있으며 약간의 양의 전하를 띤 물질층을 남길 수 있습니다.이는 주로 금속에서 발생하며, 금속에서는 결합 전자가 표면에서 단단한 벽 전위와 접촉하지 않고 오히려 상전하 흡인력에 의한 점진적인 상승 전위와 접촉합니다.표면 쌍극자의 양은 재료 표면에 있는 원자의 상세한 레이아웃에 따라 달라지며, 이는 결정면에 따라 작업 함수의 변화를 초래한다.

도핑 및 전계효과(반도체)

전자 친화성_EA E를 나타내는 반도체-진공 계면의 밴드 다이어그램. 근표면 진공 에너지_vac E와 근표면 전도 밴드 에지_C E의 차이로 정의된다.또, 다음과 같이 표시됩니다.페르미 레벨E_F, 원자가 밴드 에지_V E, 작업 함수 W.

반도체에서 작업함수는 반도체 표면의 도핑레벨에 민감하다.표면 근처의 도핑도 전계에 의해 제어될 수 있기 때문에 반도체의 작업 기능도 진공 중의 전계에 민감합니다.

의존성의 이유는 일반적으로 진공 레벨과 전도 밴드 가장자리가 도핑과 무관하게 일정한 간격을 유지하기 때문입니다.이 간격은 전자 친화력이라고 불립니다(이것은 화학의 전자 친화력과는 다른 의미를 가집니다). 예를 들어 실리콘의 전자 친화력은 4.05 ^[16]eV입니다.전자 친화도_EA E와 표면의 밴드 기준 페르미 레벨 E-E가_F_C 알려진 경우, 작업 함수는 다음과 같이 주어진다.

W=E_{\rm {EA}}+E_{\rm {C}}-E_{\rm {F}

여기서_C E는 표면에서 측정됩니다.

이것에 의해, 반도체의 대부분을 도핑 하는 것으로, 작업 기능을 튜닝 할 수 있다고 기대할 수 있다.그러나 실제로는 표면 ^[17]상태의 영향으로 인해 표면 근처의 밴드 에너지가 페르미 수준에 고정되는 경우가 많습니다.만약 표면 상태의 밀도가 높다면, 반도체의 작업 기능은 도핑이나 ^[18]전계에 대한 매우 약한 의존성을 나타낼 것입니다.

금속 작업 기능의 이론적 모델

정확한 모델은 전자적으로 많은 신체 효과와 표면 화학을 주의 깊게 다루어야 하기 때문에 작업 기능의 이론적 모델링은 어렵습니다. 이 두 가지 주제 모두 그 자체로 이미 복잡합니다.

금속 작업 기능 경향에 대한 최초의 성공적인 모델 중 하나는 젤리움 ^[19]모델입니다. 젤리움 모델은 표면 밖으로 확장되는 전자 밀도의 꼬리뿐만 아니라 갑작스러운 표면 근처의 전자 밀도(Friedel 진동과 유사함)의 진동을 가능하게 했습니다.이 모델은 (위그너-세이츠 반지름_s r로 표현되는) 전도 전자의 밀도가 작업 함수를 결정하는 데 중요한 매개 변수인 이유를 보여주었다.

젤리움 모델은 예측이 여전히 실제 업무 함수에서 상당한 편차를 보이기 때문에 부분적인 설명일 뿐이다.보다 최근의 모델들은 결정면 의존성뿐만 아니라 보다 정확한 형태의 전자 교환과 상관 효과의 포함에 초점을 맞추고 있다(이는 젤륨 ^[7]^[20]모델에서 무시되는 실제 원자 격자를 포함해야 한다).

전자 작업 기능의 온도 의존성

금속의 전자 거동은 온도에 따라 다르며 전자 작용 기능에 의해 크게 반영됩니다.Rahemi 등에 의해 개발된 전자작업함수의 온도 의존성을 예측하기 위한 이론모델은 기초 메커니즘을 설명하고 계산가능하고 측정가능한 파라미터를 통해 다양한 결정구조에 대한 이 온도 의존성을 예측한다.일반적으로 온도가 상승함에 따라 EWF는 ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ ( ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ T ) ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ 0 - ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ 0 ( k ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ T ) ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ display 0 ( \ $textstyle$ \ $varphi$ ( T ) $=$ \ $varphi$ _ { 0 } - \ $frac$ { ( k _ { \ $text$ { $B }})^{ 2$ } - $0$ $\gamma$ 0 ${\textstyle \varphi (T)=\varphi _{0}-\gamma {\frac {(k_{\text{B}}T)^{2}}{\varphi _{0}}}}$ display $displaydisplaydisplay$ displaydisplay displaydisplay displaydisplaydisplaydisplay displaydisplaydisplaydisplay 、 0 、 0 、 0 、 0 （ frac { frac { k _ frac { k _ frac { k _ ty { {CC, FCC) $\varphi _{0}$ displaystyle \ $varphi _{$ 0 $\varphi _{0}$ })은 T= $\beta$ 에서의 전자작용 함수이며, $β$ (\ $displaystyle$ \display }는 $\beta$ 변화 $\beta$ 내내 일정하다.

레퍼런스

^ ^a ^b Kittel, Charles (1996). Introduction to Solid State Physics (7th ed.). Wiley.
^ Gersten, Joel (2001). The physics and chemistry of materials. New York: Wiley. ISBN 978-0-471-05794-9. OCLC 46538642.
^ Herbert Kroemer, "준전기장과 밴드 오프셋: 전자에게 새로운 기술을 가르치다" 노벨상 강의
^ "Barrier Height Correlations and Systematics". academic.brooklyn.cuny.edu. Retrieved 11 April 2018.
^ Behunin, R. O.; Intravaia, F.; Dalvit, D. A. R.; Neto, P. A. M.; Reynaud, S. (2012). "Modeling electrostatic patch effects in Casimir force measurements". Physical Review A. 85 (1): 012504. arXiv:1108.1761. Bibcode:2012PhRvA..85a2504B. doi:10.1103/PhysRevA.85.012504. S2CID 119248753.
^ Will, C. M. (2011). "Finally, results from Gravity Probe B". Physics. 4 (43): 43. arXiv:1106.1198. Bibcode:2011PhyOJ...4...43W. doi:10.1103/Physics.4.43. S2CID 119237335.
^ ^a ^b ^c "Metal surfaces 1a". venables.asu.edu. Retrieved 11 April 2018.
^ Thomas Iii, S. W.; Vella, S. J.; Dickey, M. D.; Kaufman, G. K.; Whitesides, G. M. (2009). "Controlling the Kinetics of Contact Electrification with Patterned Surfaces". Journal of the American Chemical Society. 131 (25): 8746–8747. CiteSeerX 10.1.1.670.4392. doi:10.1021/ja902862b. PMID 19499916.
^ ^a ^b Helander, M. G.; Greiner, M. T.; Wang, Z. B.; Lu, Z. H. (2010). "Pitfalls in measuring work function using photoelectron spectroscopy". Applied Surface Science. 256 (8): 2602. Bibcode:2010ApSS..256.2602H. doi:10.1016/j.apsusc.2009.11.002.
^ ^a ^b Fernández Garrillo, P. A.; Grévin, B.; Chevalier, N.; Borowik, Ł. (2018). "Calibrated work function mapping by Kelvin probe force microscopy" (PDF). Review of Scientific Instruments. 89 (4): 043702. Bibcode:2018RScI...89d3702F. doi:10.1063/1.5007619. PMID 29716375.
^ G.L. Kulcinski, "열전자 에너지 변환" [1]
^ "Photoelectron Emission". www.virginia.edu. Retrieved 11 April 2018.
^ Dweydari, A. W.; Mee, C. H. B. (1975). "Work function measurements on (100) and (110) surfaces of silver". Physica Status Solidi A. 27 (1): 223. Bibcode:1975PSSAR..27..223D. doi:10.1002/pssa.2210270126.
^ CRC Handbook of Chemistry and Physics 버전 2008, 12–114.
^ Nikolic, M. V.; Radic, S. M.; Minic, V.; Ristic, M. M. (February 1996). "The dependence of the work function of rare earth metals on their electron structure". Microelectronics Journal. 27 (1): 93–96. doi:10.1016/0026-2692(95)00097-6. ISSN 0026-2692.
^ Virginia Semiconductor (June 2002). "The General Properties of Si, Ge, SiGe, SiO2 and Si3N4" (PDF). Retrieved 6 Jan 2019.
^ "Semiconductor Free Surfaces". academic.brooklyn.cuny.edu. Retrieved 11 April 2018.
^ Bardeen, J. (1947). "Surface States and Rectification at a Metal Semi-Conductor Contact". Physical Review. 71 (10): 717–727. Bibcode:1947PhRv...71..717B. doi:10.1103/PhysRev.71.717.
^ Lang, N.; Kohn, W. (1971). "Theory of Metal Surfaces: Work Function". Physical Review B. 3 (4): 1215. Bibcode:1971PhRvB...3.1215L. doi:10.1103/PhysRevB.3.1215.
^ Kiejna, A.; Wojciechowski, K.F. (1996). Metal Surface Electron Physics. Elsevier. ISBN 9780080536347.
^ Rahemi, Reza; Li, Dongyang (April 2015). "Variation in electron work function with temperature and its effect on the Young's modulus of metals". Scripta Materialia. 99 (2015): 41–44. arXiv:1503.08250. doi:10.1016/j.scriptamat.2014.11.022. S2CID 118420968.

추가 정보

Ashcroft; Mermin (1976). Solid State Physics. Thomson Learning, Inc.
Goldstein, Newbury; et al. (2003). Scanning Electron Microscopy and X-Ray Microanalysis. New York: Springer.

요소의 작업 기능 값에 대한 간단한 참조:

Michaelson, Herbert B. (1977). "The work function of the elements and its periodicity". J. Appl. Phys. 48 (11): 4729. Bibcode:1977JAP....48.4729M. doi:10.1063/1.323539. S2CID 122357835.

외부 링크

[Kittel-1] Kittel, Charles (1996). Introduction to Solid State Physics (7th ed.). Wiley.

[Gersten_2001-2] Gersten, Joel (2001). The physics and chemistry of materials. New York: Wiley. ISBN 978-0-471-05794-9. OCLC 46538642.

[3] Herbert Kroemer, "준전기장과 밴드 오프셋: 전자에게 새로운 기술을 가르치다" 노벨상 강의

[4] "Barrier Height Correlations and Systematics". academic.brooklyn.cuny.edu. Retrieved 11 April 2018.

[5] Behunin, R. O.; Intravaia, F.; Dalvit, D. A. R.; Neto, P. A. M.; Reynaud, S. (2012). "Modeling electrostatic patch effects in Casimir force measurements". Physical Review A. 85 (1): 012504. arXiv:1108.1761. Bibcode:2012PhRvA..85a2504B. doi:10.1103/PhysRevA.85.012504. S2CID 119248753.

[6] Will, C. M. (2011). "Finally, results from Gravity Probe B". Physics. 4 (43): 43. arXiv:1106.1198. Bibcode:2011PhyOJ...4...43W. doi:10.1103/Physics.4.43. S2CID 119237335.

[venables-7] "Metal surfaces 1a". venables.asu.edu. Retrieved 11 April 2018.

[8] Thomas Iii, S. W.; Vella, S. J.; Dickey, M. D.; Kaufman, G. K.; Whitesides, G. M. (2009). "Controlling the Kinetics of Contact Electrification with Patterned Surfaces". Journal of the American Chemical Society. 131 (25): 8746–8747. CiteSeerX 10.1.1.670.4392. doi:10.1021/ja902862b. PMID 19499916.

[pitfalls-9] Helander, M. G.; Greiner, M. T.; Wang, Z. B.; Lu, Z. H. (2010). "Pitfalls in measuring work function using photoelectron spectroscopy". Applied Surface Science. 256 (8): 2602. Bibcode:2010ApSS..256.2602H. doi:10.1016/j.apsusc.2009.11.002.

[calib-10] Fernández Garrillo, P. A.; Grévin, B.; Chevalier, N.; Borowik, Ł. (2018). "Calibrated work function mapping by Kelvin probe force microscopy" (PDF). Review of Scientific Instruments. 89 (4): 043702. Bibcode:2018RScI...89d3702F. doi:10.1063/1.5007619. PMID 29716375.

[11] G.L. Kulcinski, "열전자 에너지 변환" [1]

[12] "Photoelectron Emission". www.virginia.edu. Retrieved 11 April 2018.

[13] Dweydari, A. W.; Mee, C. H. B. (1975). "Work function measurements on (100) and (110) surfaces of silver". Physica Status Solidi A. 27 (1): 223. Bibcode:1975PSSAR..27..223D. doi:10.1002/pssa.2210270126.

[14] CRC Handbook of Chemistry and Physics 버전 2008, 12–114.

[15] Nikolic, M. V.; Radic, S. M.; Minic, V.; Ristic, M. M. (February 1996). "The dependence of the work function of rare earth metals on their electron structure". Microelectronics Journal. 27 (1): 93–96. doi:10.1016/0026-2692(95)00097-6. ISSN 0026-2692.

[16] Virginia Semiconductor (June 2002). "The General Properties of Si, Ge, SiGe, SiO2 and Si3N4" (PDF). Retrieved 6 Jan 2019.

[17] "Semiconductor Free Surfaces". academic.brooklyn.cuny.edu. Retrieved 11 April 2018.

[18] Bardeen, J. (1947). "Surface States and Rectification at a Metal Semi-Conductor Contact". Physical Review. 71 (10): 717–727. Bibcode:1947PhRv...71..717B. doi:10.1103/PhysRev.71.717.

[19] Lang, N.; Kohn, W. (1971). "Theory of Metal Surfaces: Work Function". Physical Review B. 3 (4): 1215. Bibcode:1971PhRvB...3.1215L. doi:10.1103/PhysRevB.3.1215.

[20] Kiejna, A.; Wojciechowski, K.F. (1996). Metal Surface Electron Physics. Elsevier. ISBN 9780080536347.

[21] Rahemi, Reza; Li, Dongyang (April 2015). "Variation in electron work function with temperature and its effect on the Young's modulus of metals". Scripta Materialia. 99 (2015): 41–44. arXiv:1503.08250. doi:10.1016/j.scriptamat.2014.11.022. S2CID 118420968.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

v t 열전자 밸브
이론적 원리	열전자 방출 업무기능 열음극 공간 차지 제어 그리드 억제기 그리드 양극 빛나는 양극 게터
종류들	다이오드 오디오 트라이오데 도토리관 뉴비스터 테트로이드 비임 사극 펜토데 펜타그리드(헥소드, 헵토드, 옥토드) 노노드 음극선관 애드론 역파 발진기 빔 편향 튜브 캐릭터론 콤팩트론 아이도포르 아이콘스코프 유도 출력 튜브 키네스코프 클라이스트론 매직 아이 마그네트론 모노스코프 포토튜브 광전자 증배기 셀렉트론 튜브 저장관 서튼 튜브 탈라리아 프로젝터 진행파관 트로코트론 비디오 카메라 튜브 윌리엄스 튜브 플레밍 밸브
번호부여시스템	RMA 리트마 마르코니오스람 멀라드-필립스 JIS 러시아어
예	진공관 목록 튜브 소켓 목록

Search