그랜드 캐논 앙상블

통계역학
열역학 운동 이론
입자 통계 스핀-통계 정리 동일입자 맥스웰-볼츠만 보스아인슈타인 페르미-디락 패러스타틱스 애니오닉 통계량 브레이드 통계량
열역학적 앙상블 NVE 마이크로캐논학 NVT 규범적 µVT 그랜드 캐논어 NPH 이센탈피크-이소바르어 NPT 등온-이소바르식
모델 데비예 아인슈타인 이싱 팟츠
가능성 내부 에너지 엔탈피 헬름홀츠 자유 에너지 기브스 자유 에너지 잠재력 / 란다우 자유 에너지
과학자들 맥스웰 볼츠만 깁스 아인슈타인 에렌페스트 폰 노이만 톨먼 데비예 페르미 보스
v t

통계역학에서 웅장한 규범적 앙상블(일명 매크로캐논적 앙상블)은 저장소와 열역학적 평형(열과 화학)에 있는 입자의 기계적 시스템의 가능한 상태를 나타내기 위해 사용되는 통계적 앙상블이다.^[1] 이 시스템은 시스템이 저장소와 에너지와 입자를 교환할 수 있다는 의미에서 개방되어 있어 시스템의 다양한 가능한 상태가 총 에너지와 총 입자수에서 모두 다를 수 있다고 한다. 시스템의 볼륨, 형태 및 기타 외부 좌표는 시스템의 모든 가능한 상태에서 동일하게 유지된다.

그랜드 캐논 앙상블의 열역학적 변수는 화학적 전위(심볼: µ)와 절대 온도(심볼: T. 앙상블도 부피와 같은 기계적 변수에 의존한다(기호: V) 시스템 내부 상태의 특성에 영향을 미치는 기능 따라서 이 세 가지 수량이 각각 앙상블의 상수이기 때문에 이 앙상블을 µVT 앙상블이라고 부르기도 한다.

기본 사항

간단히 말해서, 그랜드 캐논 앙상블은 다음 지수에서 주어지는 각각의 뚜렷한 미시 상태에 확률 P를 할당한다.

${\displaystyle P=e^{\frac {\Oomega +\mu N-E}{kT}},}$

여기서 N은 마이크로스테이트의 입자의 수이고 E는 마이크로스테이트의 총 에너지다. k는 볼츠만의 상수다.

숫자 Ω은 그랜드 포텐셜로 알려져 있으며 앙상블에 대해 일정하다. 단, 서로 다른 µ, V, T를 선택하면 확률과 Ω이 달라진다. 최대 잠재력 Ω은 확률 분포에 대한 정규화 인자(확률, 마이크로스테이트의 전체 집합에 걸쳐 최대 1을 추가해야 함)를 제공하는 역할과 많은 중요한 앙상블 평균은 Ω(µ, V, T) 함수에서 직접 계산할 수 있다.

둘 이상의 종류의 입자가 숫자에 따라 달라질 수 있는 경우, 확률 표현은 다음과 같이 일반화된다.

${\displaystyle P=e^{\frac {\오메가 +\mu _{1}N_{1}++\mu _{2}+\ldots +\mu _{s}N_{s}-E}{k.T}},}$

여기서 µ는₁ 첫 번째 종류의 입자에 대한 화학적 전위, N은₁ 마이크로스테이트에 있는 그러한 종류의 입자의 수, µ는₂ 두 번째 종류의 입자에 대한 화학적 전위(s는 구별되는 종류의 입자의 수)이다. 그러나 이러한 입자 번호는 신중하게 정의해야 한다(아래의 입자 번호 보존 참고 참조).

웅장한 앙상블은 도체의 전자나 공동의 광자와 같은 시스템을 설명할 때 사용하기 쉬운데, 형태는 고정되어 있지만 에너지와 입자의 수는 저장장치(예: 이 경우 전기 접지나 어두운 표면)와의 접촉으로 인해 쉽게 변동할 수 있다. 웅장한 표준 앙상블은 비 상호작용 양자 입자 시스템에 대한 페르미-디락 통계 또는 보세-아인슈타인 통계를 정확하게 도출하기 위한 자연적인 설정을 제공한다(아래 예 참조).

제형에 대한 참고 사항

An alternative formulation for the same concept writes the probability as ${\displaystyle \textstyle P={\frac {1}{\mathcal {Z}}}e^{(\mu N-E)/(kT)}}$, using the grand partition function ${\displaystyle \textstyle {\mathcal {Z}}=e^{-\Omega /(kT)}}$ rather than t그의 위대한 잠재력. 이 글의 방정식(위대한 잠재력의 측면에서)은 간단한 수학 조작에 의해 대격차 함수의 관점에서 재작성될 수 있다.

적용가능성

그랜드 캐논 앙상블은 저수지와 열·화학 평형 상태에 있는 고립된 시스템의 가능한 상태를 설명하는 앙상블이다(일반 캐논 앙상블의 열탕 유도와 유사한 선으로 파생이 진행되며, 레이프에서^[2] 찾을 수 있다). 웅장한 표준 앙상블은 크고 작은 어떤 크기의 시스템에도 적용된다. 단지 그것이 접촉하고 있는 저수지가 훨씬 더 크다고 가정할 필요가 있다(즉, 거시적인 한도를 취하기 위해서).

시스템이 열역학적 양과 진화가 잘 정의되어 있는지 확인하기 위해서는 시스템이 분리되어 있다는 조건이 필요하다.^[1] 그러나 실제로는 저수지와의 직접적인 접촉이 평형을 보장하는 것이기 때문에 저수지와의 직접적 접촉 시스템을 기술하는 데 그랜드 캐논 앙상블을 적용하는 것이 바람직하다. 이러한 경우에 웅장한 표준 앙상블의 사용은 대개 1) 접촉이 약하다고 가정하여 정당화하거나 2) 저장장치 연결의 일부를 분석 중인 시스템에 통합하여 관심 영역에 대한 연결의 영향을 올바르게 모델링한다. 또는 이론적 접근법을 사용하여 개방적인 통계적 앙상블을 제공하면서 연결의 영향을 모델링할 수 있다.

웅장한 규범적 앙상블이 등장하는 또 다른 경우는 거대하고 열역학적인 시스템(그 자체와 평형을 이루는 시스템)을 고려할 때다. 시스템의 정확한 조건이 실제로 에너지나 입자 수의 변화를 허용하지 않더라도, 거대한 표준 앙상블을 사용하여 일부 열역학적 성질의 계산을 단순화할 수 있다. 그 이유는 일단 시스템이 매우 커지면, 다양한 열역학 앙상블(마이크로캐논, 표준)이 대정론적 앙상블과 어떤 면에서는 동등하게 되기 때문이다.^{[note 1]} 물론 소규모 시스템의 경우, 다른 앙상블은 평균에서도 더 이상 동등하지 않다. 그 결과, 원핵과 같이 고정된 입자수의 작은 시스템에 적용했을 때 그랜드 캐논 앙상블은 매우 부정확할 수 있다.^[3]

특성.

잠재력, 앙상블 평균 및 정확한 차이

Ω(µ₁, …, µ_s, V, T) 함수의 부분 파생 모델은 다음과 같은 ^[1][4]중요한 표준 앙상블 평균 양을 제공한다.

정확한 차이: 위의 식을 보면 Ω 함수가 정확한 차이를 가지고 있음을 알 수 있다.

${\displaystyle d\Oomega =-SdT-\langle N_{1}\langle d\mu_{1}\langle N_{s}\langle d_{s}\langle dV.}$

열역학 제1법칙: 위의 관계를 ⟨E⟩에 대한 정확한 차이 Ω으로 대체하면, 열역학 제1법칙과 유사한 방정식이 발견된다. 단, 일부 수량에 대한 평균 기호는 제외한다.^[1]

${\displaystyle d\langle E\rangle =TdS+\mu _{1}d\langle N_{1}\langle \langle \ldots +\mu _{s}\langle N_{s}\langle -\langle p\langle dV.}$

열역학적 변동: 에너지와 입자 수의 분산은^[5][6]

${\displaystyle \langle E^{2}\angle -\langle E\angle ^{2}=kT^{2}{\frac {\partial \langle E\rangle }{\partial T}}+kT\mu _{1}{\frac {\partial \langle E\rangle }{\partial \mu _{1}}}+kT\mu _{2}{\frac {\partial \langle E\rangle }{\partial \mu _{2}}}+\ldots ,}$

${\displaystyle \langle N_{1}^{2}\langle N_{1}\langle ^{2}=kT{\frac {\partial \langle N_{1}\rangele }{\partial \langlemu _{1}.}$

변동 상관 관계: 입자 수와 에너지의 공분류는^[1]

${\displaystyle \langle N_{1}N_{2}\rangle -\langle N_{1}\rangle \langle N_{2}\rangle =kT{\frac {\partial \langle N_{2}\rangle }{\partial \mu _{1}}}=kT{\frac {\partial \langle N_{1}\rangle }{\partial \mu _{2}}}.}$

${\displaystyle \langle N_{1}E_\langle N_{1}\langle \langle E\rangele =kT{\partial \langle E\rangle }{\partial \mu _{1}}},$

앙상블 예

웅장한 표준 앙상블의 유용성은 아래 예에 설명되어 있다. 각각의 경우에, 큰 잠재력은 관계에 기초하여 계산된다.

${\displaystyle \Oomega =-kT\ln \left(\sum _{\text{microstates}e^{\frac {\mu N-E}{k){kT}\오른쪽)}$

마이크로스테이트의 확률을 최대 1까지 더하기 위해 필요한 것이다.

불연속 입자 통계

보손과 페르미온(양)

많은 비상호작용 입자가 있는 양자 시스템의 특별한 경우, 열역학은 계산하기 간단하다.^[7] 입자들은 비 상호작용적이기 때문에 일련의 단일 입자 정지 상태를 계산할 수 있으며, 각 입자는 시스템의 총 양자 상태에 포함될 수 있는 분리 가능한 부분을 나타낸다. 일단 이러한 단일 입자 정지 상태를 궤도(이러한 "상태"를 전체 다체 상태와 혼동하지 않도록 하기 위해), 각각의 가능한 내부 입자 특성(스핀 또는 양극화)이 별도의 궤도(궤도)로 계산된다는 조항으로 언급하자. 각 궤도에는 입자(또는 입자)가 점유하거나 비어 있을 수 있다.

입자들은 비 상호작용적이기 때문에, 우리는 각각의 궤도들이 별도의 열역학 시스템을 형성한다는 관점을 취할 수 있다. 따라서 각각의 궤도들은 그 자체로 거대한 규범적 앙상블이며, 그 통계는 여기서 즉시 도출될 수 있을 정도로 간단하다. i라고 표시된 하나의 궤도상에 초점을 맞추면, 이 궤도 내 N 입자의 미세 상태에 대한 총 에너지는 Nϵ가_i 될 것이다. 여기서 ϵ은_i 그 궤도상의 특징적인 에너지 수준이다. 궤도상에 대한 큰 잠재력은 궤도상이 보소닉인지 페르미온인지에 따라 두 가지 형태 중 하나에 의해 주어진다.

In each case the value ${\displaystyle \scriptstyle \langle N_{i}\rangle =-{\tfrac {\partial \Omega _{i}}{\partial \mu }}}$ gives the thermodynamic average number of particles on the orbital: the Fermi–Dirac distribution for fermions, and the Bose–Einstein distribution for bosons. 전체 시스템을 다시 한 번 생각해 보면, 모든 궤도상에 대해 Ω을_i 더하면 전체 전위가 발견된다.

구별할 수 없는 고전 입자

고전역학에서는 구별할 수 없는 입자를 고려할 수도 있다(사실, 구별할 수 없는 입자는 화학적 전위를 일관성 있게 정의하기 위한 전제 조건이며, 특정 종류의 모든 입자는 서로 교환할^[1] 수 있어야 한다). 우리는 다시 같은 종류의 여러 입자를 동일한 미세 상태의 단일 입자 위상 공간에 배치하는 것을 고려하는데, 이것을 다시 "오르비탈"이라고 부른다. 그러나, 양자역학에 비해 고전역학에서 미시국가는 위상공간에서 단 한 점을 가리키는 것이 아니라 위상공간에서 확장된 영역을 가리킨다는 사실 때문에 고전적인 경우는 복잡하다: 하나의 미시국가는 모두 구별되지만 유사한 성격을 가진 무한한 수의 상태를 포함한다. 그 결과, 다수의 입자를 동일한 궤도 안으로 배치했을 때, (계통 위상 공간에서) 입자의 전체 수집은 하나의 전체 미시상태로 계산되지 않고 오히려 미시상태의 일부분으로 계산되는데, 이는 동일한 상태(동일한 입자의 순열에 의해 형성됨)를 과대계상해서는 안 되기 때문이다. 과대계수 보정 계수는 입자수의 요인이다.

이 경우 통계는 지수 전력 시리즈의 형태를 취한다.

${\displaystyle {\begin{aigned}\Oomega _{\rm {orb}&=-kT\ln {\big(}\sum _{N=0}^{\inflat }{\frac {1}{N!}}}{{\frac {N\mu -N\epsilon _{\rm {orb}}{kT}{{\big )}\\&=-kT\ln {\big (}e^{e^{\frac {\mu -\epsilon _{\rm {orb}}}{kT}}{\\Big )}\\&=-kTe^{\frac {\mu -\epsilon _{\rm {orb}{k}{kT},\end{정렬}}$

맥스웰-볼츠만 통계량에 해당하는$$ ⟨${\displaystyle }$N ${\displaystyle \frac{{\mathrm{o}}_{}}{}{}_{}\frac{{=}_{}}{\mathrm{}}}$ = -${\displaystyle \frac{\mathrm{}}{}}$∂ ${\displaystyle \frac{{\Omega \mathrm{}}_{}}{}}$ ${\displaystyle \frac{\mu }{}}$ ${$ ㎕\$displaystyle \langle N_{\rm$ {$orb}\rangel =-{\tfrac {\partial \mo}{\orb}}}{\partial \m$ \m$$}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

고립된 원자의 이온화

원자가 중립 상태에 있는 것을 선호하는지 또는 이온화 상태에 있는 것을 선호하는지 여부를 예측하는 데 그랜드 캐논 앙상블을 사용할 수 있다. 원자는 중립에 비해 전자가 많거나 적은 전리 상태로 존재할 수 있다. 아래 나온 것처럼 이온화 상태는 환경에 따라 열역학적으로 선호될 수 있다. 원자가 중립 상태 또는 두 개의 이온화된 상태 중 하나에 있을 수 있는 단순화된 모델을 고려하십시오(세부적인 계산에는 주의^[8] 퇴행성 요소도 포함된다).

• N₀ 전자와 에너지 E로₀ 충전 중립 상태.
• 에너지 E₀ + ΔE_I + q³의 산화 상태(N₀ - 1 전자)
• 에너지가₀ 있는₀ 감소된 상태(N + 1 전자) E - ΔE_A - qϕ

여기서 ΔE와_I ΔE는_A 각각 원자의 이온화 에너지와 전자 친화력이며, ΔE는 원자 근처의 진공에서 국소 정전기 전위, -q는 전자 전하다.

따라서 이 경우 잠재력은 다음과 같이 결정된다.

${\displaystyle {\begin{aigned}\Oomega &=-kT\ln {\big (}e^{\frac {\mu N_{0}-E_}}}}{0}}}}{0}}}}{k){kT}}+e^{\frac {\mu N_{0}-\mu -E_{0}-\Delta E_{\rm{I}-q-phi }{kT}}+e^{\frac {\mu N_{0}+\mu -E_{0}+\Delta E_{{\rm{A}+q\phi}}{kT}{\Big )}.\\&=E_{0}-\mu N_{0}-kT\ln {\Big (}1+e^{-\frac {-\mu -\Delta E_{\rm}-q\phi }{{}kT}}+e^{\frac {\mu +\Delta E_{\rm{A}+q\phi }{{kT}{\Big )}.\\end{aigned}}$

이 경우 다양한 상태 간의 균형을 결정하려면 -q³ - µ의 양이 중요하다. 이 값은 원자 주위의 환경에 의해 결정된다.

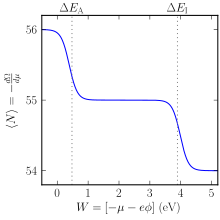
이러한 원자 중 하나를 진공 박스에 넣으면 박스 라이닝 재료의 작업 함수인 -q³ - µ = W. 다양한 고형물질의 작업함수 표와 원자종의 전자 친화력 및 이온화 에너지 표를 비교해 보면, 많은 조합이 중성 원자를 낳을 것이 분명하지만, 어떤 특정한 조합은 원자가 이온화 상태를 선호하게 될 것이다(예: 이터비움 박스의 할로겐 원자 또는 ce).텅스텐 박스에 있는 시움 원자 실온에서는 원자가 자유롭게 떠다니지 않고 상자의 노출된 라이닝에 흡착하는 경향이 있기 때문에 이 상황은 안정적이지 않다. 그러나 고온에서 원자들은 표면에서 이온 형태로 증발된다. 이 자발적인 표면 이온화 효과는 세슘 이온원으로 사용되어 왔다.^[9]

상온에서 도판 원자의 이온화가 이 앙상블에 의해 잘 묘사되는 반도체에서 이 예는 응용을 발견한다.^[8] 반도체에서 전도 대역 엣지 ϵ은_C 진공 에너지 레벨(대체 -qϕ)의 역할을 하며, µ는 페르미 레벨로 알려져 있다. 물론 도판트 원자의 이온화 에너지와 전자 친화력은 진공 값에 비해 강하게 변형된다. 실리콘, 인의 대표적인 공여 도판트는 ΔE_I = 45 mV를 가지고 있으며,^[10] 본질적인 실리콘의_C µ - µ의 값은 초기에 약 600 mV로 도판트의 이온화를 보장한다. 그러나 µ_C - µ의 값은 전기 공학에 크게 의존하므로 어떤 상황에서는 도판트를 탈이온화할 수 있다.

화학적 전위, 일반화된 "입자 번호"의 의미

입자 번호가 관련 화학적 전위를 가지려면 시스템의 내부 역학 중에 보존되어야 하며, 시스템이 외부 저장소와 입자를 교환할 때만 변경할 수 있다.

시스템의 역학 중에 에너지로 입자를 생성할 수 있는 경우, 연관된 µN 용어가 그랜드 캐논 앙상블의 확률 표현식에 나타나지 않아야 한다. 사실상 이는 그러한 종류의 입자에 대해 µ = 0을 요구하는 것과 같다. 충치벽의 흡수와 방출로 인해 숫자가 정기적으로 변하는 검은 충치 광자의 경우도 이와 같다.(반면 반사율이 높은 충치의 광자는 보존할 수 있고 0µs가 되지 않는 것을 유발할 수 있다.^[11]

어떤 경우에는 입자의 수가 보존되지 않고 N은 더 추상적으로 보존된 양을 나타낸다.

• 화학 반응: 화학반응은 한 유형의 분자를 다른 분자로 변환시킬 수 있다. 만약 반응이 일어난다면, N은_i 화학반응 중에 변하지 않도록 정의되어야 한다.
• 고에너지 입자 물리학: 일반적인 입자는 해당 항정신병 물질이 생성되면 순수한 에너지로 생성될 수 있다. 만약 이런 종류의 과정이 허용된다면, 입자의 수나 입자의 수가 보존되지 않는다. 대신 N = (입자 번호 - 항정신병자 번호)를 보존한다.^{[12][note 3]} 입자 에너지가 증가함에 따라, 입자 유형 간에 변환할 가능성이 더 많아지고, 따라서 진정으로 보존되는 숫자는 더 적다. 가장 높은 에너지에서 보존된 유일한 숫자는 전하, 약한 이소스핀, 그리고 바리온 번호인 렙톤 번호뿐이다.

한편, 어떤 경우에는 한 종류의 입자가 여러 개의 보존 숫자를 가질 수도 있다.

• 닫힌 컴파트먼트: 에너지를 공유하지만 입자를 공유하지 않는 다중 구획으로 구성된 시스템에서는 각 구획에 대해 화학 전위를 별도로 설정할 수 있다. 예를 들어, 콘덴서는 두 개의 분리된 도체로 구성되며 전자 화학 전위의 차이를 적용하여 충전된다.
• 느린 등가진동: 어떤 준균형 상황에서는 동일한 위치에 동일한 종류의 입자의 두 개의 구별되는 모집단을 둘 수 있는데, 각각은 내부적으로 평형화되지만 서로 평형화되지 않는다. 정확히 평형상태는 아니지만, 다른 모집단 간에 차이가 있을 수 있는 준균형 화학적 전위성의 명칭을 지정하는 것이 유용할 수 있다. 예: (반도체 물리학) 전도 대역과 발랑 대역의 구별되는 준페르미 수준(전자의 화학적 전위), (스핀트로닉스) 구별되는 스핀업 및 스핀다운 화학적 전위, (결정학) 구별되는 파라수소 및 정형수소 화학적 전위.

앙상블에 대한 정확한 표현

통계적 앙상블에 대한 정확한 수학적 표현은 "마이크로스테이트"의 개념이 상당히 다르기 때문에 고려 중인 역학의 유형(양 또는 고전)에 따라 뚜렷한 형태를 가진다. 양자역학에서, 대각선화는 각각 잘 정의된 에너지와 입자 수를 가진, 시스템의 뚜렷한 미세현상들을 제공하기 때문에, 원대한 규범적 앙상블은 간단한 설명을 제공한다. 고전적인 기계 케이스는 고정된 상태가 아니라 표준 위상 공간보다 통합된 상태를 포함하기 때문에 더 복잡하다.

양자역학

양자역학에서 통계적 앙상블은 $밀도{\displaystyle \stackrel{}{}}$ 행렬로 표현되며, ^ ${\displaystyle \stackrel{}{^}}$ ${\$로 표시된다$.$ 웅장한 표준 앙상블은 밀도 행렬이다^{[citation needed]}.

${\displaystyle {\hat {\rho }=\exp {\big(}{\tfrac {1}{k)T}}(\Oomega +\mu _{1}{{1}_{1}+\ldots +\mu _{s}{\hat{N}_{s}-{\hat {H}}{\big )}}}}}}$

여기서 ĥ은 시스템의 총 에너지 연산자(해밀턴어), N̂₁는 타입 1의 입자에 대한 시스템의 총 입자 번호 연산자, N̂₂는 타입 2의 입자에 대한 총 입자 번호 연산자, 기타 등등. exp는 매트릭스 지수 연산자다. 최대 잠재력 Ω은 밀도 매트릭스의 ${\displaystyle \mathrm{트레이스}}$가 1인 T r condition ^ =${\displaystyle \stackrel{}{}}$1${\displaystyle Tr{\rho }:{\$rho $}=1}$인 확률 표준화 조건에 의해 결정된다$.$

${\displaystyle e^{-{\frac {\Oomega}{k}T}}}=\operatorname {Tr} \exp {\big (}{\tfrac {1}{k)T}}}(\mu _{1}{{1}{{N}_{1}+\ldots +\mu _{s}{{N}_{s}-{\hat {H}}{\big )}.}$

그랜드 앙상블의 경우 연산자 Ⅱ, N̂₁ 등의 기본 상태는 모두 Fock 공간에 여러 개의 입자가 있는 상태이며, 밀도 매트릭스는 동일한 기준으로 정의된다. 에너지와 입자수는 모두 별도로 보존되기 때문에 이들 운영자는 상호 통근하고 있다.

(에너지 및 입자수 연산자의 상호 통근 특성을 고려할 때) 동시 고유성 ψ_i⟩의 완전한 기초를 찾을 수 있으므로 대정합주체는 브라켓 표기법을 사용하여 간단한 형태로 작성될 수 있다. 여기서 ĥ_i = = E_ii ,, N̂₁ = N_i1,ii ⟩ 등. 그런 고유기반을 감안할 때, 웅대한 규범적 앙상블은 단순하다.

${\displaystyle {\hat {\rho }}}=\sum _{i}e^{\frac {\\mo_{1}N_{1}{1,i}+\ldots +\mu _{s}N_{s}-E_}}{i}}}}{kT}} \psi _{i}\랑글 \langle \psi _{i}}$

${\displaystyle e^{-{\frac {\Oomega}{k}T}}}=\sum _{i}e^{\frac {\mu _{1}N_{1,i}+\ldots +\mu _{s}N_{s}-E_}}}{{i}}}}}}{k}T}}.}$

여기서 합계는 상태_i I의 총 에너지, 유형 1의_1,i N 입자, 유형 2의 N_2,i 입자 등을 갖는 상태의 전체 집합에 걸쳐 있다.

고전 기계학

고전 역학에서, 웅장한 앙상블 대신에 그 p1, 쭉 펼쳐져 pn과 q1, 쭉 펼쳐져 qn 있는 정준 좌표 자유의 시스템의 내부도( 일반화된 momenta과 일반화된 좌표) 결합 확률 밀도 함수 다양한 치수의 여러 단계 이상의 남자 공간들을 정의한 ρ(N1, 쭉 펼쳐져 Nsp1, 쭉 펼쳐져 pn, q1, 쭉 펼쳐져 qn),로 표시됩니다.. 웅장한 정설앙상블의 표현은 다음과 같은 점에서 정설앙상블보다 다소 섬세하다.^[1]

• 입자의 수와 따라서 좌표 n은 상공간마다 다르다.
• 유사한 입자의 허용이 구별되는 상태로 간주되는지 여부를 고려하는 것이 중요하다.

입자의 시스템에서 자유도 n의 수는 물리적 상황에 따라 달라지는 방식으로 입자의 수에 따라 달라진다. 예를 들어, 모노아텀s n = 3N의 3차원 기체에서는, 그러나 분자 가스에서는 또한 회전과 진동 자유도가 존재할 것이다.

웅장한 표준 앙상블의 확률밀도함수는 다음과 같다.

${\displaystyle \rho ={\frac {1}{h^{n}C}e^{\frac {\frac {\Oomega +\mu _{1}N_{1}+\ldots +\mu _{s}-{s}-E}{1}kT}},}$

어디에

• E는 시스템의 에너지로서, 위상의 함수(N₁, …N_s, p₁, …p_n, q_1n),
• h는 에너지×시간의 단위로 임의적이지만 미리 결정된 상수로, 하나의 마이크로 상태의 범위를 설정하고 정확한 치수를 ρ에 제공한다.^{[note 4]}
• C는 N₁, …N의_s 함수인 과대계수 보정계수(아래 참조)이다.

다시 Ω 값은 ρ이 정규화된 확률밀도함수라고 요구함으로써 결정된다.

${\displaystyle e^{-{\frac {\Oomega}{k}T}}}=\sum _{N_{1}=0}^{\infty }\ldots \sum _{N_{s}=0}^{\infty }\int \ldots \int {\frac {1}{h^{n}C}}e^{\frac {\mu _{1}N_{1}+\ldots +\mu _{s}N_{s}-E}{kT}}\,dp_{1}\ldots dq_{n}}$

이 적분은 주어진 입자 수에 대해 사용 가능한 위상 공간 전체를 차지한다.

과대계수수정

유체의 통계적 역학(가스, 액체, 플라스마)에서 잘 알려진 문제는 성질이 비슷하거나 동일한 입자를 처리하는 방법이다. 입자를 구별할 수 있는 입자로 간주해야 하는가, 그렇지 않은가? 이 시스템의 운동 방정식에서 각 입자는 구별 가능한 실체로 영원히 추적된다. 그러나 각 입자의 위치가 단순히 교환된 시스템의 유효한 상태도 있다. 이러한 상태는 위상 공간의 서로 다른 위치에 나타나지만 동등한 것처럼 보인다.

유사한 입자의 순열이 구별되는 상태로 간주되는 경우 위의 요인 C는 단순히 C = 1. 이 관점에서 앙상블은 모든 순열 상태를 별도의 미세 상태로 포함한다. 처음에는 양성인 것처럼 보이지만, 이는 오늘날 기브스의 역설로 알려진 표준 앙상블에서 심각한 비폭력의 엔트로피 문제를 초래한다. 웅장한 표준 앙상블에서 추가적인 논리적 불일치가 발생한다: 구별 가능한 순열의 수는 시스템 내의 입자 수뿐만 아니라 저장소에 있는 입자 수(시스템이 저장소와 입자를 교환할 수 있기 때문에)에 따라 달라진다. 이 경우 엔트로피와 화학적 전위는 비확장성이지만 관련이 없어야 하는 매개변수(저수지 크기)에 따라 정의되지 않는다.

이러한 문제를 해결하려면 두 개의 유사한 입자(시스템 내부 또는 시스템과 저장장치 간)의 교환이 시스템의 뚜렷한 상태를 주는 것으로 간주되어서는 안 된다.^{[1][note 5]} 이 사실을 통합하기 위해 통합은 여전히 전체 위상 공간에 걸쳐 수행되지만 결과는 다음과 같이 나뉜다.

$[\displaystyle C=N_{1}!N_{2}!\ldots N_{s}!,}$

가능한 다른 순열의 수입니다. C에 의한 분할은 모든 위상 공간에 걸쳐 적분에서 발생하는 오버카운팅을 깔끔하게 수정한다.

각 구별 가능한 타입 $i{\displaystyle }$ ${\displaystyle i}$은(는) 별도의 입자 $계수기{\displaystyle {}_{}}$ N ${\displaystyle i_{}}${\$displaystyle N_{i}$와 화학 전위 ${\displaystyle {\mu i}_{}}${\$displaystyle \mu _{i$에 의해 추적되므로$$, 대정규학적 앙상블에 구별 가능한 유형의 입자를 포함시키는 것이 물론 가능하다. 웅장한 표준 앙상블에서 "완전히 구별 가능한" 입자는 가능한 모든 구별 가능한 형태의 입자를 고려하고, 각각의 가능한 모든 유형을 별도의 입자 계수기와 분리된 화학 전위로 추적하는 것이다.

메모들

참조