데카르트의 폴륨

기하학에서 데카르트의 엽은 방정식에 의해 정의된 대수곡선이다.

${\displaystyle x^{}}$ ${\displaystyle {3\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ -${\displaystyle {}^{}3}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle y}$= ${\displaystyle 0}$ ${\$ x$^{3}+y^{3}-3axy=0\,}$.

그 이름은 "잎"을 뜻하는 라틴어 엽에서 유래되었다.

역사

이 곡선은 1638년 르네 데카르트에 의해 처음 제안되고 연구되었다.^[1] 그 명성에 대한 주장은 미적분학의 발달에 관한 사건에 있다. 데카르트는 최근 페르마트가 접선선을 찾는 방법을 발견했기 때문에 임의의 지점에서 곡선에 대한 접선선을 찾으라고 피에르 드 페르마에게 도전했다. 페르마트는 데카르트가 할 수 없는 일을 쉽게 해결했다.^[2] 미적분학의 발명 이후, 접선선의 경사는 암묵적인 분화를 이용하여 쉽게 찾을 수 있다.^[3]

곡선 그래프 작성

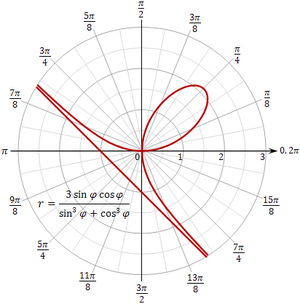
데카르트의 엽은 극좌표로 표현할 수 있다.

${\displaystyle r={\frac {3a\sin \theta \coses \coses \coses \coses \coses \}{3}\coses }},}$

왼쪽에 있는 것. 이것은^[4] 와 같다.

${\displaystyle r={\frac {3a\sec \tan \tan \tan \tan }{1+\tan ^{3}\ta }}.}$

$또{\displaystyle }$ 다른 기법은 y${\displaystyle }$= ${\displaystyle p}$ ${\displaystyle x}$ ${\displaystyle y=px}$을(를) 쓰고 p ${\displaystyle x}$ 및$$ $y{\displaystyle }$ ${\displaystyle y}$에 대해 $p{\displaystyle }$ ${\displaystyle p}$의 관점에서 푸는$$ 것이다$.$ 이렇게 하면 합리적인 파라메트릭 방정식이 나온다.^[5]

${\$$$$}}}}\,y={3ap^{2}} \{1+p^{3$$}}}{3 이상$$}}}}$.

매개변수가 다음과 같이 곡선의 위치와 관련됨을 알 수 있다.

• <- ${\displaystyle p<-1}$은(는) > 0 ${\displaystyle$ x$>0$ < ${\displaystyle y<0}$: 오른쪽, 아래쪽, "윙"에 해당한다.
• $><1<p>$는 x > 0 $<<\displaystyle x<0$ > $<<\displaystyle y>0$ : 왼쪽, 위쪽 "윙"에 해당한다.
• > ${\displaystyle p>0}$은(는) > 0 ${\displaystyle x>0$ > ${\displaystyle$ y$>0$ : 곡선의 루프에 해당한다.

$함수$를 표시하는 또 다른 방법은 y = ${\displaystyle y=x}$에 대한 대칭에서 도출할 수 있다$.$ 대칭은 그 방정식에서 직접 볼 수 있다(x와 y는 상호 교환할 수 있다). 예를 들어 45°CW의 회전을 적용하면 X축의 회전과 대칭으로 함수를 표시할 수 있다.

이 작업은 다음과 같은 대체 작업에 해당한다.

${\displaystyle x={{u+v} \over {\sqrt{2}}}\,y={{u-v} \\sqrt{2}}:$

수확량

${\displaystyle v=\pm u{\sqrt{3a{\sqrt{2}}~2}}:{6u+3a{\sqrt{2}}:}}}$

$({\displaystyle u}$, ${\displaystyle v}$) ${\displaystyle (u,v)}$의 데카르트 시스템에서 플로팅하면 엽이$$ 45° 회전하여 $u{\displaystyle }$ ${\displaystyle u}$ - 축에$$ 의해 대칭이 된다.

특성.

제1 사분면에 고리를 형성하며, 원점에는 2점, 점근은 무증상이다.

${\displaystyle \mathrm{x}}$+ ${\displaystyle y}$+ ${\displaystyle a}$= 0 ${\$

선 $y{\displaystyle }$= ${\displaystyle x}$ ${\displaystyle y=x$$}$을(를) 대칭으로 한다$.$ 따라서 두 선은 원점과 지점$({\displaystyle }$3 $a$/ ${\displaystyle 2\mathrm{}}$,$$ $a$/ 2${\displaystyle }$)에서 $교차$한다$.$

암묵적 분화는 이 곡선에 대한 접선 선의 기울기가 다음과^[3] 같은 공식을 제공한다.

${\displaystyle {\frac}{dx}={\frac {ay-x^{2}}:{y^{2}-ax}}}}$

위의 극성 표현 중 하나를 사용하여 루프의 내부 면적은 $3{\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$ $[\displaystyle 3a^{2}/2$}인 것으로 확인되며$,$ 곡선의 "윙"과 기울어진 점증상 사이의 영역도 또한 ${\displaystyle {}^{}}$ a ${\displaystyle {2\mathrm{}}^{}2\mathrm{}}$ ${\displaystyle 3a^{2}$이다$.$^[1]

맥클라우린의 트라이섹트릭스와의 관계

데카르트의 엽은 아핀 변환에 의한 마클로린의 삼색트릭스와 관련이 있다. 이를 확인하려면 방정식부터 시작하십시오.

${\displaystyle x^{}}$ ${\displaystyle {3\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$= ${\displaystyle 3}$ ${\displaystyle a}$ x ${\displaystyle y}$ ${\$ x$^{3}+y^{3}=3axy$

그리고 45도 회전 좌표계의 방정식을 찾기 위해 변수를 변경한다. 이것은 설정에 해당된다.

${\displaystyle x={X+Y} \over {\sqrt{2},y={X-Y} \over {\sqrt{2}}.}$

$X{\displaystyle }$, ${\displaystyle Y}$ ${\displaystyle X,Y}$ 평면에서$$ 방정식은 다음과 같다.

${\displaystyle 2X(X^{2}+3$$$$Y^{2}=3{\sqrt{2}a(X^{2}-Y^{2}})}$.

$Y{\displaystyle \sqrt{\mathrm{}}}$ ${\displaystyle Y}$ 방향으로$$ 곡선을 3 ${\$의 계수로 확장하면 이 값은$$

${\displaystyle 2X(X^{2}+)Y^{2}=a{\sqrt{2}(3X^{2}-Y^{2}),}$

매클라우린의 트리섹트릭스 방정식이야

메모들

참조

• J. 데니스 로렌스: 1972년 도버 출판사의 특별 평면 곡선의 카탈로그. ISBN 0-486-60288-5, 페이지 106-108
• 조지 F. 시몬스: 미적분 젬스: 짧은 삶과 기억나는 수학, 1992년 뉴욕, 맥그라우 힐, xiv,355 ISBN 0-07-057566-5; 2007년 신판 The Mathemical Association of America(MAA)

외부 링크

위키미디어 커먼즈에는 데카르트의 폴륨과 관련된 미디어가 있다.

• Weisstein, Eric W. "Folium of Descartes". MathWorld.
• 맥튜터의 유명한 곡선지수에서 "데카르트의 사람들"
• 매트릭커브의 "카테시안 폴륨"