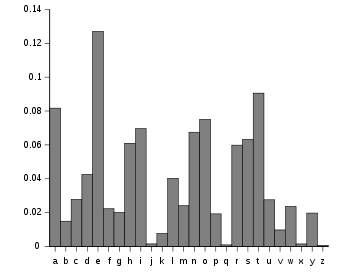
주파수 분석

Frequency analysis
다른 용도는 주파수 분석(동음이의)을 참조하십시오.
영어 텍스트의 일반적인 문자 배포입니다.취약한 암호는 배포를 충분히 마스킹하지 않으며 암호 분석가가 이를 이용하여 메시지를 읽을 수 있습니다.

암호 해석학에서 빈도 분석(문자 카운트라고도 함)은 암호문 내의 문자 또는 문자 그룹의 빈도에 대한 연구입니다.그 방법은 고전적인 암호를 해독하는 데 도움이 된다.

빈도 분석은 주어진 문자 언어 범위에서 특정 문자와 문자의 조합이 다양한 빈도로 발생한다는 사실에 기초한다.게다가, 그 언어의 거의 모든 샘플에서 거의 같은 문자의 특징적인 분포가 있다.예를 들어, 영어 섹션의 , 및 가 가장 일반적인 반면 , 및 은 희귀합니다.마찬가지로 , , , 및 는 가장 일반적인 문자 쌍(큰 문자 또는 디그래프)이고 , , , , 는 가장 일반적인 [1]반복입니다."ETAOIN SHRDLU"라는 말도 안 되는 문구는 전형적인 영어 텍스트에서 가장 많이 사용되는 12개의 글자를 나타냅니다.

일부 암호에서는 자연어 평문의 이러한 특성이 암호문에 보존되어 있으며, 이러한 패턴은 암호문만의 공격에 악용될 가능성이 있다.

단순 치환 암호의 주파수 분석

단순 치환 암호에서는 평문의 각 문자가 다른 문자로 대체되며 평문의 특정 문자는 항상 암호문의 동일한 문자로 변환됩니다.예를 들어, 레터의 모든 항목이 레터로 바뀌었을 경우, 레터의 수많은 인스턴스를 포함하는 암호문 메시지가 를 나타내는 암호분석 전문가에게 제안됩니다.

주파수 분석의 기본 용도는 우선 암호문자의 빈도를 세고 추측된 평문자를 관련짓는 것입니다.암호문 내의 s가 다른 어떤 것보다 많으면 그것이 보통 텍스트에 대응한다고 생각되지만 이는 확실치 않습니다.또한 영어에서도 매우 일반적이기 때문에 둘 중 하나일 수도 있습니다.그것은 평문일 가능성이 낮거나 덜 흔하다.따라서 암호 분석가는 암호문자와 일반문자의 매핑을 여러 가지 조합으로 시도해야 할 수 있습니다.

문자 쌍(큰 문자), 세 쌍둥이(트리거) 등의 수를 고려하는 등 통계의 보다 복잡한 사용을 생각할 수 있다.이는 예를 들어 암호 분석가에게 더 많은 정보를 제공하기 위해 수행되며, 거의 항상 영어로 같은 순서로 함께 발생합니다. 비록 그 자체는 드물지만요.

예

Eve가 아래의 암호문을 가로채고 다음과 같이 간단한 치환 암호를 사용하여 암호화되어 있다고 가정합니다.

리빗츠위브위크위크위크위크익스위크익스위크익스위클리키픽스피키위스위스퍼림 WQLermglimXXXX리위크ITWAWSQWXXWXXXXXRSJ GSTVRIEYVIXCVMUIMWERGMIWXMJMGCSMWX조미QXLIVIQIVIXQSVSTWHKPEGARCSXRWIIBXV IZMXFSJX라이크개WIWIWIXLIVXLIRGIIBIMYLXSJX림브릿지XXEAMWYEPP XLMWYRMWXGSWRMHIVEXMSMSTHPHPHPHPXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXPHPHPHPHPHPHPHPHPHPHPHPHPHPHPHPHPHPHPXXXXXXXXXXXXXXXXXXIVJSVLMSMSWVIRCXMWYMX

이 예에서는 대문자는 암호문을 나타내고 소문자는 평문을 나타내며(t또는 추측), ~는 암호문이 평문을 나타낸다는 추측을 나타내기 위해 사용됩니다.

이브는 주파수 분석을 사용하여 다음 행에 따라 메시지를 해결할 수 있습니다. 암호문자의 개수는 가장 일반적인 단일 문자,[2] 가장 일반적인 빅그램 및 가장 일반적인 트리거임을 나타냅니다.e 영어에서 가장 흔한 문자이고, 가장 흔한 빅램이며, 가장 흔한 삼각법이다.이것은 ~,th ~, ~Ie을 강하게 시사한다.암호문자에서 두 번째로 흔한 문자는 영어에서 첫 번째와 두 번째로 빈번한 문자와 설명되고 있기 때문에, 이브는 a~가 세 번째로 빈번한 문자인 것으로 추측한다.이러한 전제조건에 따라 다음과 같은 부분 복호화 메시지를 얻을 수 있습니다. 

HeVeTCSWPeYVaVSReQMthaYVaOeaWHRTatePFaMVaWHKVSTYZethKEetPeJVSZaYPaRRGaReM WQhMtQaReWGPSReHMtQaRaKeaKeaTtMJTPRGaVaKaeTRAWHATTHATTHATTMZeTWATSWATTVaPMRTRSJGSTVReaYVetCVMUeRMeWtMGCSMWtJOMeQtheVSTWHKPaGARCStrweEAVSWeeBtVeZMTFSJKAGAAWHaPSWYSWeWeAVStheVtheRGaPeRQeBGeeHMWYPFhaVHAWHa WHYPSRFQMtha PPtheaCCeaVaWGeSJKTV WMRheHYSPHeQeMYHTSJtheMWReGtQaRoEVeZaaKPeaWHTAAMWYAPP thMWYRMWtSGSWRMHeVatMSWMGSTPHhaVHPFKPazeNTCMTEVJSVhMSMSWeRCeGtMWYM

이러한 초기 추측을 이용하여, 이브는 ""와 that같은 그녀의 선택을 확인하는 패턴을 발견할 수 있다.게다가, 다른 패턴들은 더 많은 추측을 암시한다.""Rtate는 states~를 의미하는 ""일 수 있으며,atthattMZe 마찬가지로 ""는 ~와 m~를 생성하는 i""atthattime로 추측할 수 있다.게다가 heVe「」는 here「~」r를 주는 것일지도 모른다.이 추측을 채우면서, 이브는 다음과 같이 된다.

여기서 TCSWPeYraWHarSseQithaYraOeaWHstate PFairaWHKRSTYHtmetheKeetPeJrSmaYPassGasei WQhiGhitQaseWGPSseHitQasaKeaTtiJTPsGaraKaeTsa그때TWAWSQWattTraPistsSJ GSTrseaYreatCriUeiWasGiWtiJiGCSiWtJOieQeretQSRSTWHKPAGACSTS웨어SWeeBtr 방출FSJtheKaGAAWHaPSWYSWeStherthesGaPesQereeBGeeHiWYPFharHaWHIPSSSFQithaPPtheaCCearaWGeSJKTrWisheHYSPHeQeiYhtSJWseGtQasOerFremarAaKPeaWHTAAiWYaPP thiWysiWGSWsiHeratiSWiGSTHarHPFKPameNTCiterJSrhisSCiWiSWresCeGtiWYit

그 결과, 이러한 추측은 다른 것(예를 들어,remarA ""k는 ~을 암시하는 ""remark일 수 있음) 등을 시사하며, 나머지 문자를 추론하는 것은 비교적 간단하며, 결국 평문을 산출한다. 

이 때문에, 폐색되어 있던 아글라스카세이 nauglasscasei nautifulscarabaeus와 그 당시 알려지지 않은 자연주의자의 코스로서 우리는 근원적인 흑색 스포트 근방에 있는 광우병 emandritiity emandlanderenalongeneatherstelleshandscarviewswehandlassechandlassechandlasscandlandlandsweeshandlandsweeshandlandsweateshandlandlandlandlandsoeshandsechands그 무게감은 매우 주목할 만했고 모든 것을 고려하기 위해 그것을 존중하는 것에 대해 맹렬히 비난해야 했다.

이 때 이브가 공백과 구두점을 삽입하는 것이 좋습니다.

그러자 레그랑드는 엄숙하고 위풍당당한 태도로 일어나 딱정벌레가 들어 있는 유리 상자에서 내게 가져다 주었다.그것은 아름다운 스카라베우스였고, 그 당시에는 자연학자들에게 알려지지 않은-물론 과학적인 관점에서 보면 큰 상이었다.등 한쪽 끝 부근에 동그란 검은 점이 두 개 있고 다른 쪽 끝에는 긴 점이 하나 있었다.비늘은 매우 단단하고 광택이 났으며 금빛을 발하고 있었다.곤충의 무게는 매우 놀라웠고, 모든 것을 고려했을 때, 나는 목성의 그것에 대한 의견을 탓할 수 없었다.

The Gold-Bug의 이 예에서는 이브의 추측이 모두 맞았다.그러나 이러한 경우가 항상 있는 것은 아닙니다. 개별 평문에 대한 통계량의 변동은 초기 추측이 틀렸다는 것을 의미할 수 있습니다.잘못된 추측을 역추적하거나 위의 예에서 제시된 다소 단순화된 정당성보다 훨씬 더 깊이 있는 통계 분석이 필요할 수 있습니다.

또한 일반 텍스트가 예상된 문자 빈도 분포를 나타내지 않을 수도 있습니다.메시지가 짧을수록 더 많은 변화가 나타날 수 있습니다.인위적으로 왜곡된 텍스트를 작성할 수도 있습니다.예를 들어, 전체 소설은 ""라는 e글자를 모두 생략한 채 쓰이고 있는데, 이는 리포그램으로 알려진 문학의 한 형태이다.

이력 및 사용방법

알 킨디의 9세기 암호 메시지 해독 원고 첫 페이지
아랍어 문자 빈도 분포.

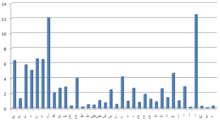
주파수 분석(실제로 모든 종류의 암호 분석)에 대한 최초의 기록된 설명은 9세기에 아랍의 수학자인 알 킨디에 의해 암호 [3]메시지 해독에 관한 필사본에서 제공되었습니다.아랍어에 특징적인 문자 빈도가 [4]있다는 것을 처음으로 밝혀낸 것은 코란에 대한 면밀한 텍스트 연구였다.그것의 사용은 확산되었고, 비슷한 시스템은 르네상스 시대에 유럽 국가들에서 널리 사용되었다.1474년까지 시코 시모네타는 라틴어와 이탈리아어의 [5]암호 해독에 관한 매뉴얼을 작성했다.

간단한 대체 암호화의 이러한 약점을 극복하기 위해 암호학자들이 몇 가지 계획을 고안했습니다.다음과 같은 것이 있습니다.

  • 동음이의 대체:동음이의 사용: 모노알파벳 치환 암호의 가장 일반적인 문자에 대한 몇 가지 대체 방법.예를 들어 영어의 경우 X 암호문과 Y 암호문이 모두 일반 텍스트E 를 의미할 수 있습니다.
  • 폴리알파벳 치환, 즉 여러 알파벳을 사용한다.다양한 방법으로 선택된다(Leone Alberti가 이것을 최초로 제안한 것 같다).
  • 폴리그래픽 치환, 예를 들어 19세기 중반에 찰스 휘트스톤이 발명한 Playfair 암호와 같이 평문자의 쌍 또는 세 쌍이 치환을 위한 단위로 취급되는 체계입니다.

이러한 주파수 카운트 공격의 단점은 암호화와 복호화가 모두 복잡해져 오류가 발생한다는 것입니다.영국의 한 외무장관이 플레이페어 암호를 거부한 것은 휘트스톤과 플레이페어가 보여준 것처럼 남학생들이 성공적으로 대처할 수 있었다고 해도, "우리의 보좌관들은 절대 그것을 배울 수 없었다!"는 이유에서라고 한다.

20세기 전반의 회전자 기계(예: Enigma 기계)는 기본적으로 간단한 주파수 분석의 영향을 받지 않았다.그러나 다른 종류의 분석("공격")을 통해 이러한 머신 중 일부에서 메시지가 성공적으로 디코딩되었습니다.

스페인어로 된 편지 빈도.

빈도 분석을 위해서는 평문 언어의 통계와 문제 해결 기술에 대한 기본적인 이해만 필요하며, 손으로 수행하는 경우 광범위한 서신 부기에 대한 내성이 필요합니다.제2차 세계대전 동안, 영국과 미국 모두 주요 신문에 십자말 퍼즐을 게재하고 누가 가장 빨리 풀 수 있는지를 겨루어 코드브레이커를 모집했다.추축국이 사용하는 암호는 주파수 분석을 통해 해독할 수 있는 것이 몇 가지 있는데, 예를 들어 일본인이 사용하는 영사 암호도 있습니다.문자 계수 및 통계 분석의 기계적 방법(일반적으로 IBM 카드 유형 기계)은 제2차 세계대전 때 처음 사용되었으며, 아마도 미국 육군의 SIS에 의해 사용되었을 것입니다.오늘날, 문자 세기와 분석의 힘든 작업은 컴퓨터 소프트웨어로 대체되었고, 컴퓨터 소프트웨어는 이러한 분석을 몇 초 만에 수행할 수 있다.현대의 컴퓨팅 능력에서는 기존의 암호로는 기밀 데이터를 실질적으로 보호할 수 없습니다.

픽션의 주파수 분석

댄싱맨의 암호문 일부

주파수 분석은 소설로 묘사되었다.에드거 앨런 포의 "황금벌레"와 아서 코난 도일 경의 셜록 홈즈 이야기 "춤추는 사람의 모험"은 단순한 대체 암호를 공격하기 위해 주파수 분석을 사용하는 것을 묘사한 이야기의 예이다.포 이야기 속 암호는 몇 가지 속임수로 뒤덮여 있지만, 이것은 암호학적으로 중요한 어떤 것보다도 문학적 장치에 가깝다.

「 」를 참조해 주세요.

추가 정보

  • Helen Fouché Gaines, "암호분석", 1939년, 도버. ISBN0-486-20097-3
  • Abraham Sinkov, "초급 암호 분석:"A Mathemical approach", The Mathemical Association of America, 1966.ISBN 0-88385-622-0.

레퍼런스

  1. ^ Singh, Simon. "The Black Chamber: Hints and Tips". Retrieved 26 October 2010.
  2. ^ "A worked example of the method from bill's "A security site.com"". Archived from the original on 2013-10-20. Retrieved 2012-12-31.
  3. ^ 이브라힘 A. Al-Kadi "암호학의 기원:아랍의 공헌", Cryptologia, 16(2)(1992년 4월) 페이지 97~126.
  4. ^ "In Our Time: Cryptography". BBC Radio 4. Retrieved 29 April 2012.
  5. ^ Kahn, David L. (1996). The codebreakers: the story of secret writing. New York: Scribner. ISBN 0-684-83130-9.

외부 링크