퓨전 트리

컴퓨터 과학에서 퓨전 트리는 유한한 우주의 w비트 정수에 연관 배열을 구현하는 트리 데이터 구조의 한 종류이며, 여기서 각 입력 정수는 크기가^w 2 미만이고 음이 아닙니다.n개의 키-값 $쌍$ 으로 구성된 컬렉션에서 동작하는 $경우$ O $(n$ ) 공간을 $사용$ 하여_w $O ($ log n) $시간$ 내에 검색을 수행합니다. 이는 기존의 자가 밸런싱 바이너리 검색 트리보다 점근적으로 빠르며 w의 $큰$ 값에 대해서도 van Emde Boas 트리보다 우수합니다.이 속도는 머신워드에서 실행할 수 있는 일정한 시간 연산을 사용하여 달성됩니다.퓨전 트리는 1990년 마이클 프레드먼과 댄 윌러드에 ^[1]의해 발명되었다.

프레드먼과 윌러드의 1990년 원본 논문 이후 몇 가지 진전이 있었다.1999년에는^[2] 알고리즘의 모든 기본 연산이 AC에 속하는⁰ 계산 모델 하에서 퓨전 트리를 구현하는 방법이 제시되었으며, AC는 추가 및 비트 단위 부울 연산을 허용하지만 원래의 퓨전 트리 알고리즘에서 사용되는 곱셈 연산을 허용하지 않는 회로 복잡도 모델이다.해시 테이블을 사용하는 퓨전 트리의 동적 버전은 1996년에^[3] 제안되었으며, 이는 예상대로 원래 구조의 $O (log w$ n $)$ 런타임과 일치했다.지수 트리를 사용하는 또 다른 동적 버전은 2007년에^[4] 제안되었으며, 이 버전은 연산당 최악의 경우 $O w$ ( $log n$ + $log$ n $)$ 의 $실행$ 시간을 산출합니다.동적 융합 트리가 높은 확률로 연산당 O $(log w$ n $)$ 를 $달성$ 할 수 있을지는 미해결 상태로 남아 있다.

이 데이터 구조는 쿼리 키보다 작은 최대 키 값 또는 쿼리 키보다 큰 최소 키 값으로 출력을 제공하는 이전 키 및 후속 키 검색 작업에 유용합니다.일정 시간 내에 가장 중요한 비트 로케이터의 부분적인 결과도 많은 추가 연구에 도움이 되었습니다.이 작업이 효율적인 주된 이유는 단어 수준의 병렬화를 도입하기 때문입니다.즉, 여러 단어에 대한 연산이 동시에 이루어지기 때문에 전체 연산 수가 필요한 것보다 훨씬 적습니다.이 데이터 구조에서 수행할 수 있는 다른 작업은 키를 추가하고 키를 제거하는 것입니다.

구조

융접 트리는 기본적으로 분기 $계수$ 가^1/5 w인 B-트리로, O $(log w$ n $)$ 의 높이를 제공하는 트리의 높이에 큰 영향을 주지 않기 때문에 작은 지수도 가능합니다.업데이트 및 쿼리에 필요한 런타임에 도달하려면 퓨전 트리가 최대 $w개$ 의^1/5 키를 포함하는 노드를 일정한 시간에 검색할 수 있어야 합니다.이는 키를 압축("스케치")하여 모든 것이 하나의 기계 단어에 들어갈 수 있도록 함으로써 이루어집니다.이것에 의해, 병렬로 비교가 가능하게 됩니다.따라서 스케치, 병렬 비교 및 가장 중요한 비트 인덱스 로케이터를 포함한 일련의 연산을 통해 필요한 솔루션에 도달할 수 있습니다.

스케치

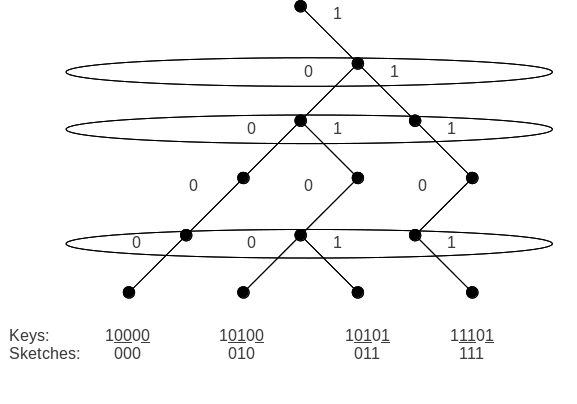
스케치란 k개의 키를 $포함$ 하는 노드의 각 w비트 $키$ 를 k - $1비트$ 로 압축하는 방법입니다.각 $키$ x는 루트에서 시작하여 x에 $대응$ 하는 리프에서 끝나는 $높이$ w의 풀 바이너리 트리 내의 경로로 생각할 수 있다.이 경로는 일반적으로 모든 비트가 스캔될 때까지 i의 왼쪽 아이(ith 비트가 0인 경우)와 오른쪽 아이(ith 비트가 1인 경우)를 재귀적으로 검색하여 처리할 수 있습니다.두 경로를 구별하려면 분기점(두 키가 서로 다른 첫 번째 비트)을 보면 됩니다.최대 k개의 키가 있기 때문에 k-1개 이상의 분기점은 존재하지 않습니다.즉, 키를 식별하는 데 필요한 것은 k-1비트 이하입니다.따라서 k-1비트보다 큰 스케치는 없습니다.

스케치 함수의 중요한 특성은 키의 순서를 유지하는 것입니다.즉, 임의의 $2개$ 의 키 x < y에 대해 $sketch$ $($ x) < sketch( $y)>$ 이므로 키의 전체 범위에 대해 sketch(x₀₁) <...<binary(x_k-1)> 왜냐하면 바이너리 트리와 같은 경로를 따를 경우 노드가 x<x₁<...와 같은 순서로₀ 정렬되기 때문입니다.<x_k-1.

스케치 근사

스케치 비트의 위치가 b₁ < b₂ < · · < b_r >인 경우, 키_w-1 x · · xx₁₀ 의 스케치는 r 비트 $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ x $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ - 1 $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ x b $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ 1 (\ $display$ style $x_{b_{r}x_{b_1}}\cdots x_{b_{$ 1 $x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}$ 입니다.

C 프로그래밍 언어와 같은 표준 단어 연산만으로 일정한 시간에 키의 완벽한 스케치를 직접 계산하기는 어렵습니다.대신 스케치 비트는 대략적인 스케치라고 불리는 비트 AND 및 곱셈을 사용하여 최대⁴ r의 크기 범위로 패킹할 수 있습니다. 이 스케치에는 모든 중요한 비트는 물론 예측 가능한 패턴으로 퍼져 있는 일부 불필요한 비트가 있습니다.비트 AND 연산은 키에서 이러한 모든 비스케치 비트를 제거하는 마스크 역할을 하며 곱셈은 스케치 비트를 작은 범위로 이동합니다."완벽한" 스케치와 마찬가지로 대략적인 스케치는 키의 순서를 유지하며 스케치(x₀)<sketch(x₁)<...<block(x_k-1)>를 참조해 주세요.

올바른 곱셈 상수를 결정하려면 몇 가지 전처리가 필요합니다.위치_i b의 각 스케치 비트는 m = $\textstyle \sum _{i=1}^{r}$ $\textstyle \sum _{i=1}^{r}$ $\textstyle \sum _{i=1}^{r}$ r \ $displaystyle \textstyle \sum$ _ ${i=1}^{r}$ 2의 $\textstyle \sum _{{i=1}}^{r}$ ^m_i 곱셈을 통해 b + m으로_i 이동합니다_i.대략적인 스케치가 작동하려면 다음 세 가지 특성이 있어야 합니다.

b_i + m은_j 모든 쌍(i, j)에 대해 구별됩니다.그러면 스케치 비트가 곱셈에 의해 손상되지 않습니다.
b_i + m은_i i의 엄밀하게 증가하는 함수이다.즉, 스케치 비트의 순서는 x'm에서도 유지됩니다.
(b_r + m_r) - (b₁ + m₁) r⁴ r. 즉, 스케치 비트는 최대⁴ r의 크기 범위(r w O(w^1/5))로 채워진다.

유도 인수는 m이_i 어떻게 구성될 수 있는지를 보여줍니다.m₁ = w - b로₁ 하자.1 < t µ r과 m₁, m₂...m이_t-1 이미 선택되었다고 가정합니다.그런 다음 속성 (1)과 (2)가 모두 충족될 수 있도록 가장_t 작은 정수 m을 선택합니다.속성(1)에서는 모든 1 µ i, j µ r 및 1 µ l µ t-1에 대해 m µ_i b - b_j + m이_l 필요합니다_t.따라서 m이 피해야 할 값은_t tr µr보다²³ 작습니다.m은 최소값으로 선택되므로_t (b_t + m_t) ( (b_t-1 + m_t-1) + r³. 이는 속성 (3)을 의미합니다.

대략적인 스케치는 다음과 같이 계산됩니다.

비트 AND가 x와 $\sum _{i=0}^{r-1}2^{b_{i}}$ i $\sum _{i=0}^{r-1}2^{b_{i}}$ r - 1 2 b i { $displaystyle \sum$ _ { $i$ }^{ $r-1} 2^{b_{i$ 인 스케치 비트를 제외한 모든 비트를 마스크합니다.
위에서 계산한 대로 키에 미리 정해진 상수 m을 곱합니다.이 작업에는 실제로 두 개의 기계어가 필요하지만, 이 작업은 일정한 시간 내에 수행할 수 있습니다.
시프트된 스케치 비트를 제외한 모든 비트를 마스크합니다.이것들은 현재 최대⁴ r < w비트의^4/5 연속된 블록에 포함되어 있습니다.

병렬 비교

스케치에 의한 압축의 목적은 모든 키를 하나의 w비트 워드에 저장하는 것입니다.노드의 노드 스케치를 비트 문자열로 합니다.

1sketch(x₁) 1sketch(x₂)...sketch(x_k)

여기서 모든 스케치 워드는 각각에 설정된 비트를 부가하여 하나의 문자열로 묶는다.스케치 함수는 정확히 b µr⁴ 비트를 사용한다고 가정할 수 있습니다.그 후 각 블록은 1 + b µ^4/5 w비트를 사용합니다.k µ^1/5 w이기 때문에 노드 스케치 내의 비트 수는 최대 w가 됩니다.

간단한 알림은 제외하고 비트 문자열 s와 음이 아닌 정수 m의 경우 s는 s를 m회 그 자체에 연결하는 것을 나타냅니다^m.t가 비트 문자열인 경우 st는 t와 s의 연결을 나타냅니다.

노드 스케치를 사용하면 임의의 b비트 정수 y 키를 검색할 수 있습니다.z = (0y),^k 이것은 노드 스케치의 각 워드를 한 번의 작업으로 쿼리 정수 y와 비교할 수 있도록 노드가 스케치하는 한 일정 시간(상수(01^b)^k으로 계산할 수 있으며 워드 수준의 병렬성을 입증할 수 있도록 합니다.y의 길이가 5비트일 경우 스케치(y)^k를 얻기 위해 000001....000001을 곱합니다.sketch_i(x)와 0y의 차이는 sketch(y) ${\$ \displaystyle \ $leq$ } sketch(x_i)인 $\leq$ 경우에만 각 블록의 선행 비트가 1이 됩니다.따라서 다음과 같이 최소 지수 i를 계산할 수 있다.sketch(x_i) y y는 다음과 같다.

노드 스케치에서 z를 뺍니다.
차이의 비트 AND와 상수(10^b)^k를 구합니다.그러면 각 블록의 선두 비트를 제외한 모든 비트가 지워집니다.
결과의 가장 중요한 비트를 찾아 쿼리 스케치보다 작은 스케치를 가진 요소에서 쿼리 스케치보다 큰 요소로의 정확한 전환 인덱스를 식별합니다.
i번째 블록의 선두 비트가 인덱스 i(b+1)를 가지고 있다는 사실을 사용하여 스케치의 순위인 i를 계산합니다.

데스크에칭

임의 쿼리 q에 대해 병렬 비교는 다음과 같이 지수 i를 계산합니다.

sketch10_i-1 ≤sketch(q) ≤sketch(x_i)

모든 값의 스케치 중 q의 스케치 위치가 모든 실제 값에서 q의 위치와 동일하지 않을 수 있기 때문에 아쉽게도 q의 정확한 이전 또는 후속이 됩니다.모든 키 중에서 x 또는_i x의_i-1 공통 프레픽스가 q와 가장 긴 것은 사실입니다.이는 q와 공통 프레픽스가 긴 키y도 q와 공통되는 스케치비트가 많아지기 때문입니다sketch(y) 에 더 가깝습니다.sketch(q) 어떤 것보다도sketch(x_j)

2개의 w비트 정수 a와 b 사이의 가장 긴 공통 프리픽스는 a와 b 사이의 비트 단위 XOR의 최상위 비트를 찾아 일정한 시간에 계산할 수 있습니다.다음으로 가장 긴 공통 프레픽스를 제외한 모든 프레픽스를 마스크하기 위해 사용할 수 있습니다.

p는 일련의 키에서 q가 분기하는 위치를 정확하게 식별합니다.q의 다음 비트가 0일 경우 q의 후속 비트가 p1 서브트리에 포함되어 q의 다음 비트가 1일 경우 q의 이전 비트가 p0 서브트리에 포함되어 있습니다.이를 통해 q의 정확한 위치를 결정하기 위한 다음 알고리즘을 제안합니다.

병렬 비교를 사용하여 다음과 같은 지수 i를 구합니다.sketch10_i-1 ≤sketch(q) ≤sketch(x_i)
가장 긴 공통 프리픽스 p(q)와 x 또는_i x 중 하나를_i-1 계산합니다(둘 중 긴 것을 사용).
l-1을 가장 긴 공통 프리픽스 p의 길이라고 합니다.
1. q의 l번째 비트가 0일 경우 e = p10이라고^w-l 합니다.병렬 비교를 사용하여 다음 항목을 검색합니다.sketch(e) 이것은 q의 실제 이전 버전이다.
2. q의 l번째 비트가 1이면 e = p01로^w-l 한다.병렬 비교를 사용하여 이전 버전을 검색합니다.sketch(e) 이것이 q의 실제 후계자.
q의 이전 또는 후속 중 하나가 발견되면 키 세트 중 q의 정확한 위치가 결정됩니다.

퓨전 해시

해시테이블에 대한 퓨전트리의 응용은 Willard에 의해 제공되었으며, Willard는 해시체인을 포함한 외부 레벨 해시테이블과 각 해시체인을 나타내는 퓨전트리가 결합되는 해시용 데이터 구조를 기술한다.해시체인에서는 부하계수가 일정한 해시테이블에서는 체인의 평균 사이즈는 일정하지만 모든 체인의 $사이즈$ 는 O $(log$ n $/log$ $log$ n $)$ 이며, $여기$ 서 n은 해시된 항목의 수이다.이 체인 크기는 퓨전 트리가 작업당 일정한 시간에 검색 및 업데이트를 처리할 수 있을 정도로 작습니다.따라서 데이터 구조의 모든 작업에 대한 시간은 높은 확률로 일정합니다.보다 정확하게는, 이 데이터 구조에서, 모든 역-다중공칭 $확률$ p $(n)$ = $exp(log$ n $) O (1)$ 에 대해, $시간$ C를 초과하는 연산이 존재할 확률이 $최대$ p $(n)$ ^[5]가 되도록 $상수$ C가 존재한다.

레퍼런스

^ 를 클릭합니다Fredman, M. L.; Willard, D. E. (1990), "BLASTING Through the Information Theoretic Barrier with FUSION TREES", Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing (STOC '90), New York, NY, USA: ACM, pp. 1–7, doi:10.1145/100216.100217, ISBN 0-89791-361-2.
^ 를 클릭합니다Andersson, Arne; Miltersen, Peter Bro; Thorup, Mikkel (1999), "Fusion trees can be implemented with $AC 0$ instructions only", Theoretical Computer Science, 215 (1–2): 337–344, doi:10.1016/S0304-3975(98)00172-8, MR 1678804.
^ 를 클릭합니다Raman, Rajeev (1996), "Priority queues: small, monotone and trans-dichotomous", Fourth Annual European Symposium on Algorithms (ESA '96), Barcelona, Spain, September 25–27, 1996, Lecture Notes in Computer Science, vol. 1136, Berlin: Springer-Verlag, pp. 121–137, doi:10.1007/3-540-61680-2_51, MR 1469229.
^ 를 클릭합니다Andersson, Arne; Thorup, Mikkel (2007), "Dynamic ordered sets with exponential search trees", Journal of the ACM, 54 (3): A13, arXiv:cs/0210006, doi:10.1145/1236457.1236460, MR 2314255.
^ 를 클릭합니다Willard, Dan E. (2000), "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree", SIAM Journal on Computing, 29 (3): 1030–1049, doi:10.1137/S0097539797322425, MR 1740562.

외부 링크

MIT CS 6.897: 고급 데이터 구조: 강의 4: 퓨전 트리, 교수님.Erik Demaine (2003년 봄)
MIT CS 6.897: 고급 데이터 구조: 강의 5, 더 많은 퓨전 트리, 자기 조직적인 데이터 구조, 전면 이동, 정적 최적성, 교수Erik Demaine (2003년 봄)
MIT CS 6.851: 고급 데이터 구조: 강의 13, 퓨전 트리 노트입니다, 교수님.Erik Demaine (2007년 봄)
MIT CS 6.851: 고급 데이터 구조: 강의 12, 퓨전 트리 노트입니다, 교수님.Erik Demaine (2012년 봄)

[1] 를 클릭합니다Fredman, M. L.; Willard, D. E. (1990), "BLASTING Through the Information Theoretic Barrier with FUSION TREES", Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing (STOC '90), New York, NY, USA: ACM, pp. 1–7, doi:10.1145/100216.100217, ISBN 0-89791-361-2.

[2] 를 클릭합니다Andersson, Arne; Miltersen, Peter Bro; Thorup, Mikkel (1999), "Fusion trees can be implemented with $AC 0$ instructions only", Theoretical Computer Science, 215 (1–2): 337–344, doi:10.1016/S0304-3975(98)00172-8, MR 1678804.

[3] 를 클릭합니다Raman, Rajeev (1996), "Priority queues: small, monotone and trans-dichotomous", Fourth Annual European Symposium on Algorithms (ESA '96), Barcelona, Spain, September 25–27, 1996, Lecture Notes in Computer Science, vol. 1136, Berlin: Springer-Verlag, pp. 121–137, doi:10.1007/3-540-61680-2_51, MR 1469229.

[4] 를 클릭합니다Andersson, Arne; Thorup, Mikkel (2007), "Dynamic ordered sets with exponential search trees", Journal of the ACM, 54 (3): A13, arXiv:cs/0210006, doi:10.1145/1236457.1236460, MR 2314255.

[5] 를 클릭합니다Willard, Dan E. (2000), "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree", SIAM Journal on Computing, 29 (3): 1030–1049, doi:10.1137/S0097539797322425, MR 1740562.

[1]

[2]

[3]

[4]

[5]

v t 트리 데이터 구조
트리 검색 (다이나믹 세트/어소시에이션 어레이)	2–3 2–3–4 AA (a, b) AVL B B+ B* B^x. (최적) 바이너리 검색 춤추다 HTree 간격 주문통계 (좌향) 레드-블랙 희생양 스플라이 T 나무 UB 무게 밸런스
수북이	바이너리 이항 브로달 피보나치 좌파 페어링 스큐 판 엠데 보아스 약한
시도하다	Ctrie C-trie(압축 ADT) 해시 기수 서픽스 삼진수 검색 X-Fast 고속
공간 데이터 파티션 트리	공 BK BSP 데카르트어 힐베르트 R k-d(표준 k-d) M 미터법 MVP 옥트리 PH 우선 순위 R 쿼드 R R+ R* 부분 부사장 X
기타 트리	덮다 지수 펜윅 손가락. 프랙탈 트리 인덱스 퓨전 해시 캘린더 i디스턴스 K-ary 좌측자녀 우측자매 링크/컷 로그 구조화 결합 머클 p q. 범위 SPQR 정상

Search