붉은-검은 나무
Red–black tree| 붉은-검은 나무 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 유형 | 나무 | ||||||||||||||||||||||||||||
| 발명된 | 1972 | ||||||||||||||||||||||||||||
| 발명된 사람 | 루돌프 바이어 | ||||||||||||||||||||||||||||
| 큰 O 표기법의 복잡성 | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
컴퓨터 과학에서, 적색-검은 일종의 자기 균형 이진 검색 트리다.각 노드는 삽입 및 삭제 시 트리의 균형을 유지하는 데 사용되는 "색상"("빨간색" 또는 "검은색")을 나타내는 여분의 비트를 저장한다.[3]
트리가 수정되면 새 트리는 다시 배열되고 "다시 칠"되어 최악의 경우 나무가 얼마나 불균형해질 수 있는지 구속하는 색소 특성을 복원한다.속성 재배치와 회수가 효율적으로 수행될 수 있도록 설계된다.
재균형이 완벽하지는 않지만 ) O 시간 내 검색을 보장하며, 여기서 은(는) 항목 수입니다.트리 재배열 및 회수 작업과 함께 삽입 및 삭제 작업도 O) O n시간에 수행된다.[4]
각 노드의 색상을 추적하려면 색상이 두 개뿐이기 때문에 노드당 1비트 정보만 있으면 된다.트리에는 빨간색-검은색 트리에 특정한 다른 데이터가 포함되어 있지 않으므로, 메모리 설치 공간은 고전적인 (코어링되지 않은) 이진 검색 트리의 그것과 거의 동일하다.많은 경우, 추가 정보 비트는 추가 메모리 비용 없이 저장할 수 있다.
역사
1972년 루돌프 바이엘은[5] B-트리의 특별한 주문-4 케이스인 데이터 구조를 발명했다.이 나무들은 같은 수의 노드로 뿌리부터 잎까지 모든 경로를 유지하여 완벽하게 균형 잡힌 나무를 만들었다.하지만, 그것들은 바이너리 검색 트리는 아니었다.바이엘은 논문에서 그들을 "대칭적 이진수 B-트리"라고 불렀고, 후에 그들은 2–3–4 나무 또는 단지 2–4 나무로 유명해졌다.[6]
1978년 논문 '균형있는 나무를 위한 이분법적 틀'에서 레오니다스 J. 기바스와 로버트 세지윅은 대칭적인 2진법 B-트리로부터 적-검은 나무를 도출했다.[7][8]'빨간색'은 제록스 PARC에서 근무하면서 저자들이 사용할 수 있는 컬러 레이저 프린터가 제작한 가장 잘 생긴 색이기 때문에 선택됐다.[9]기바스의 또 다른 반응은 나무를 그릴 수 있는 빨간색과 검은색 펜 때문이라고 말한다.[10]
1993년 아르네 안데르손은 삽입과 삭제 작업을 간소화하기 위해 오른쪽 기울어진 나무의 아이디어를 소개했다.[11]
1999년, Chris Okasaki는 삽입 작업을 순수하게 기능하게 만드는 방법을 보여주었다.밸런스 기능은 4개의 불균형 케이스와 1개의 디폴트 밸런스 케이스만을 관리해야 했다.[12]
원래의 알고리즘은 8개의 불균형 사례를 사용했지만, 코멘 외 연구진. (2001) 이를 불균형 사례 6개로 줄였다.[3]세지윅은 46줄의 자바 코드만으로 인서트 작업이 가능하다는 것을 보여주었다.[13][14]2008년 세지윅은 삽입과 삭제 작업을 단순화한다는 안데르손의 생각을 살려 좌편향 적색-흑색 트리를 제안했다.세지윅은 원래 두 아이가 붉은색인 노드를 허용해 나무가 2~3~4그루의 나무처럼 만들었지만, 이후 이 제한이 추가돼 새로운 나무는 2~3그루의 나무처럼 되었다.세지윅은 인서트 알고리즘을 단 33줄로 구현하여 원래 코드 46줄을 상당히 단축시켰다.[15][16]
용어.
적색-흑색 트리는 컴퓨터 공학에서 텍스트 조각이나 숫자(예: 그림 1과 2의 숫자)와 같이 비교 가능한 데이터의 조각을 조직하는 데 사용되는 특별한 유형의 이진 검색 트리다.키 및/또는 데이터를 운반하는 노드를 흔히 "내부 노드"라고 부르지만, 이를 매우 구체적으로 하기 위해 이 문서에서는 비 NIL 노드라고도 부른다.
빨간색-검은색 나무의 잎 노드(그림 1의 NIL)는 키나 데이터를 포함하지 않는다.이러한 "리브"는 컴퓨터 메모리에 명시적인 개인이 될 필요는 없다. NULL 포인터는 모든 이진 트리 데이터 구조에서와 같이 (상위) 노드의 이 위치에 하위 노드가 없다는 사실을 암호화할 수 있다.그럼에도 불구하고, 트리에서 이들의 위치에 따라, 이러한 물체는 RB 구조와 관련된 다른 노드와 관련되며, 부모, 형제(즉 부모의 다른 자식), 삼촌, 조카 노드, 심지어 자식 노드일 수 있지만, 다른 노드의 부모일 수는 없다.이 조건의 "색상"은 "경로 끝 객체에" 귀속시킬 필요는 없다.NIL또는BLACK"는 " is"라는 조건에 의해 암시된다.NIL(이 발언도 참조).
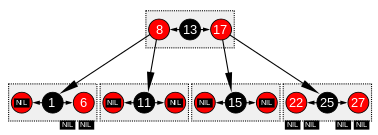
그림 2는 이러한 NIL 잎이 없는 개념적으로 동일한 빨간색-검은색 나무를 보여준다.동일한 경로 개념에 도달하기 위해서는 예를 들어, 3개의 경로가 노드 1을 통과한다는 것, 즉 1left+2의right 추가 경로를 통과하는 경로, 즉left 6과right 6의 경로를 통과한다는 것을 알아야 한다.이 방법으로, 이 경로의 끝은 또한 그림 1의 NIL 잎과 완전히 동등한 새 노드의 도킹 지점이다.
반면에, 한계적인 실행 시간을 절약하기 위해, 이러한 (아마도 많은) NIL 잎은 (값 NULL의 포인터 대신) 하나의 고유한 (및 검은색) 센티넬 노드에 대한 포인터로 구현될 수 있다.
결론적으로 어린이가 존재하지 않는다는 사실(참 노드가 아니며 데이터를 포함하지 않음)은 모든 발생에서 동일한 NULL 포인터 또는 보초 노드에 대한 동일한 포인터로 지정할 수 있다.이 글 전체에서 어느 하나를 선택하든 NIL 노드라고 하며 일정한 값을 갖는다. NIL.
노드의 검은 깊이는 루트부터 그 노드에 이르는 검은 노드의 수(즉, 검은 선조들의 수)로 정의된다.적색-흑색 트리의 검은 높이는 뿌리부터 잎까지의 경로에 있는 흑색 노드의 수로서, 요건 4에 의해 일정하게 된다(대안적으로 어떤 잎 노드의 검은 깊이로도 정의할 수 있다).[17]: 154–165 노드의 검은 높이는 노드에 의해 뿌리내린 하위 트리의 검은 높이다.이 글에서 NIL 노드의 하위 트리는 그림 2에서 제시한 바와 같이 비어 있고 트리 높이도 0이므로 NIL 노드의 검은색 높이는 0으로 설정해야 한다.
특성.
이진 검색 트리에 부과된 요구 사항 외에 적색-흑색 트리가 다음을 충족해야 한다.[18]
- 각 노드는 빨간색 또는 검은색이다.
- 모든 NIL 노드(그림 1)는 검은색으로 간주된다.
- 빨간 노드는 빨간 아이를 갖지 않는다.
- 지정된 노드에서 하위 NIL 노드로 가는 모든 경로는 동일한 수의 검은색 노드를 통과한다.
코멘 & 알과 같은 일부 저자들은 [18]"뿌리가 검은 것"을 다섯 번째 요건이라고 주장하지만 멜혼 & 샌더스나[17] 세지윅 & 웨인은 그렇지 않다.[16]: 432–447 뿌리는 항상 적색에서 흑색으로 바꿀 수 있기 때문에 이 규칙은 분석에 거의 영향을 미치지 않는다.이 글은 또한 그것을 생략하는데, 그것은 재귀적 알고리즘과 증거를 약간 방해하기 때문이다.
예를 들어, 블랙 노드만으로 구성된 모든 완벽한 이진 트리는 레드-블랙 트리다.
검색 또는 트리 통과와 같은 읽기 전용 작업은 요구 사항에 영향을 주지 않는다.한편, 수정작업은 요건 1과 2를 쉽게 유지하지만, 다른 요건과 관련하여, '적색폭행'이라 불리는 요건 3의 위반 또는 '흑색폭행'이라 불리는 요건 4의 도입을 피하기 위해 약간의 추가적인 노력을 기울여야 한다.
이 요구사항은 적색-흑색 나무의 중요 특성을 강제한다. 즉, 뿌리부터 가장 먼 잎까지의 경로는 뿌리부터 가장 가까운 잎까지의 경로의 두 배 이상 길지 않다.그 결과 나무의 높이가 균형이 잡혔다.값 삽입, 삭제, 찾기 등의 작업은 트리의 h 에 비례하는 최악의 시간을 요구하므로, 높이에 대한 이 상한은 최악의 경우, 즉 항목 n{\의 로그(즉, o O( ){)에서 적색-검은 나무를 효율적으로 만들 수 있다.는 일반 바이너리 검색 트리의 경우는 그렇지 않다.수학적 증명은 교정쇄 단원을 참조하십시오.
빨간색-검은색 트리는 모든 이진 검색 트리와 마찬가지로 매우 효율적인 순차적 액세스(예: 순서상 통과, 즉 왼쪽-루트-오른쪽 순서로)를 허용한다.그러나 그들은 또한 root에서 leaf까지 트래버설을 통한 점증적으로 최적의 직접 액세스를 지원하여 O ) O n 검색 시간을 발생시킨다.
주문서 4의 B-tree와 유사함
적색-흑색 트리는 각 노드가 1에서 3 사이의 값과 2에서 4개의 어린이 포인터 사이의 (귀납적으로) 포함할 수 있는 순서[19] 4의 B-트리와 구조가 유사하다.그러한 B-트리에서는 각 노드가 빨간색-검은색 트리의 검은색 노드에 있는 값과 일치하는 값을 하나만 포함하며, 동일한 노드 앞뒤에 있는 선택적 값은 빨간색-검은색 트리의 동등한 빨간색 노드와 일치한다.
이러한 동등성을 확인하는 한 가지 방법은 빨간색-검은색 트리를 그래픽으로 표현하여 빨간색 노드가 부모 검은색 노드와 수평으로 정렬되도록 수평 클러스터를 함께 만들어 "위로 이동"하는 것이다.B-트리 또는 빨간색-검은색 트리의 수정된 그래픽 표현에서 모든 리프 노드는 동일한 깊이에 있다.
빨간색-검은색 트리는 구조적으로 순서 4의 B 트리와 동등하며, 최소 충만 계수는 클러스터당 값의 33%이고 최대 용량은 3개이다.
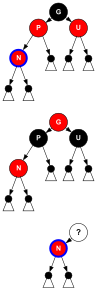
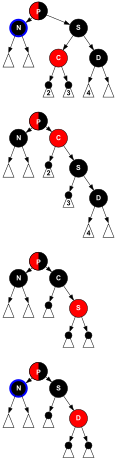
이 B-트리 유형은 적-검은 나무 변환에서 모호성을 허용하기 때문에 적-검은 나무보다 더 일반적이지만, 적-검은 나무 순서 4의 등가 B-트리로부터 여러 개의 적-검은 나무를 생성할 수 있다(그림 3 참조).B-트리 클러스터가 1개의 값만 포함하는 경우 최소값인 검은색이며 두 개의 자식 포인터가 있다.클러스터에 3개의 값이 포함되어 있는 경우, 중앙값은 검은색이고, 각 값은 옆에 저장된 값이 빨간색이 된다.그러나 클러스터에 두 개의 값이 포함되어 있으면 한 개의 값이 빨간색-검은색 트리의 검은색 노드가 될 수 있으며 다른 하나는 빨간색이다.
따라서 순서-4 B-트리는 각 군집에 포함된 값 중 어느 것이 전체 군집의 루트 블랙 트리인지 그리고 동일한 군집의 다른 값의 상위인지를 유지하지 않는다.그럼에도 불구하고 적색-흑색 나무의 수술은 가치의 벡터를 유지할 필요가 없기 때문에 적색-흑색 나무의 수술이 제때에 더 경제적이다.[20]값을 참조로 저장하기보다는 각 노드에 직접 저장하면 비용이 많이 들 수 있다.그러나 B-트리 노드는 각 노드의 색상 속성을 저장할 필요가 없기 때문에 공간이 더 경제적이다.대신 클러스터 벡터에서 어떤 슬롯이 사용되는지 알아야 한다.예를 들어, 객체와 같이 값이 참조에 의해 저장되는 경우 null 참조를 사용할 수 있으므로, 클러스터는 값 포인터의 슬롯 3개와 트리의 하위 참조의 슬롯 4개를 포함하는 벡터로 나타낼 수 있다.그 경우, B-트리는 메모리에서 더 콤팩트해질 수 있어 데이터 인접성을 개선할 수 있다.
구조적으로 색상이 있는 이진수 나무와 같은 큰 순서를 가진 B-tree에서도 같은 유추를 할 수 있다. 단지 더 많은 색이 필요할 뿐이다.파란색을 추가한 다음 청색-적색-흑색 트리를 빨간색-흑색 나무와 같이 정의하지만, 계층의 두 연속 노드가 파란색이 아니며 모든 청색 노드가 빨간색 노드의 자식 노드가 된다는 추가적인 제약조건이 있는 경우, 이 트리는 청색, 적색, bl 등 최대 7개의 값을 가진 군집을 가진 B-트리와 동일하다고 가정합시다.ue, black, blue, red, blue (각 클러스터의 경우, 최대 1개의 검은색 노드, 2개의 빨간색 노드, 4개의 파란색 노드가 있을 것이다.)
적당한 양의 값의 경우 색상이 있는 이진 트리는 각 수평 노드 클러스터의 채우기 계수를 최대화하려고 시도하지 않기 때문에(색상이 있는 이진 트리에서는 최소 채우기 계수만 보장되므로 클러스터의 분할 또는 결합 횟수가 제한됨) 색상이 있는 이진 트리에 비해 삽입 및 삭제 속도가 빠르다.B-tree는 회전을 수행하는 데 더 빠를 것이다(색상 이진 트리에 여러 개의 개별 노드를 두는 것보다 동일한 클러스터 내에서 회전이 자주 발생하기 때문이다).그러나 대용량 저장의 경우 B-tree는 로컬에서 액세스할 수 있는 동일한 클러스터에 여러 명의 어린이를 그룹화하여 더욱 소형화되므로 훨씬 더 빠를 것이다.
군집의 평균 채우기 계수를 증가시키기 위해 B-tree에서 가능한 모든 최적화는 등가의 다중색 이진수에서 가능하다.특히 구조적으로 동등한 B-트리에서의 평균 채우기 계수를 최대화하는 것은 비흑색 노드의 수를 늘림으로써 다색 트리의 총 높이를 줄이는 것과 같다.최악의 경우는 컬러 바이너리 트리의 모든 노드가 검은색일 때 발생하며, 가장 좋은 경우는 3분의 1만 검정(그리고 나머지 3분의 2는 빨간색 노드)일 때 발생한다.
적색-흑색 트리는 삽입 시간, 삭제 시간, 검색 시간 등에 대해 최악의 경우를 보장한다.이는 실시간 애플리케이션과 같이 시간에 민감한 애플리케이션에서 유용할 뿐만 아니라 최악의 경우 보증을 제공하는 다른 데이터 구조에서 중요한 구성 요소를 만든다. 예를 들어, 컴퓨터 기하학에 사용되는 많은 데이터 구조는 적색-흑색 나무와 커러에 사용되는 완전 공정 스케줄러에 기초할 수 있다.리눅스 커널과 epoll 시스템 호출 구현은[21] 적색-흑색 트리를 사용한다.
AVL 트리는 ) 검색, 삽입 및 제거를 지원하는 또 다른 구조물이다.AVL 트리는 빨강-검은 색상이 될 수 있으므로 RB 트리의 하위 집합이다.최악의 경우 높이가 RB 나무의 0.720배여서 AVL 나무의 균형이 더 단단하다.79회 주행에서 실제 시험 케이스를 가진 벤 파프의 성능 측정에서는 AVL 대 RB 비율이 0.677과 1.077 사이, 중위수가 0.947이고 기하 평균이 0.910이다.[22]WAVL 트리는 그 두 나무 사이에서 공연을 한다.
적색-흑색 트리는 기능 프로그래밍에서도 특히 중요하며, 기능 프로그래밍에서는 가장 일반적인 영구 데이터 구조 중 하나로서 돌연변이 후 이전 버전을 유지할 수 있는 연관 배열과 세트를 구성하는데 사용된다.빨간색-검은색 나무의 영구 버전은 시간 외에도 삽입 또는 삭제 시마다 O O n의 공간이 필요하다.
2-4 트리마다 동일한 순서로 데이터 요소를 가진 적색 흑색 트리가 있다.2~4그루의 나무에 대한 삽입·삭제작업도 적색-검은 나무의 색채 플립과 회전에 해당한다.이것은 2-4그루의 나무를 적-흑-흑 나무의 이면을 이해하는 중요한 도구로 만들고, 2-4그루의 나무를 실제로 자주 사용하지 않더라도 적-흑-흑 나무 바로 앞에 2-4그루의 나무를 도입하는 알고리즘 입문서가 많은 이유다.
2008년, 세지윅은 이전에 불특정화된 이행의 자유도를 제거함으로써, 왼쪽 편향 적색 흑색 나무라고[23] 하는 보다 단순한 버전의 적색 흑색 나무를 도입했다.LLRB는 삽입 및 삭제 중을 제외하고 모든 빨간색 링크가 왼쪽으로 기울어져야 하는 추가 불변성을 유지한다.적색-흑색 나무는 2-3그루의 나무 또는 [24]2-4그루의 나무 중 하나에 대해 등축적으로 만들 수 있다.[23]2–4 나무 등각도는 1978년 Sedgewick에 의해 설명되었다.[7]2-4그루의 나무를 가지고, 이등분법은 분할에 해당하는 "색깔 뒤집기"로 해결되는데, 두 아이 노드의 빨간색이 아이들을 떠나 부모 노드로 이동한다.
빠른 검색을 위해 최적화된 나무의 일종인 탱고 트리의 원래 설명은 특히 데이터 구조의 일부로 빨간색-검은색 트리를 사용한다.[25]
Java 8의 경우, 해시맵을 수정하여 LinkedList를 사용하여 충돌 해시코드로 다른 요소를 저장하는 대신, 적색-흑색 트리를 사용하도록 하였다.따라서 요소를 (m) 에서 m) m으)로 검색하는 시간 복잡성이 개선되며, 서 m 은 충돌 해시코드가 있는 요소의 수입니다.[26]
운영
적색-흑색 트리에서 검색 또는 트리 통과와 같은 읽기 전용 작업은 모든 적색-흑색 트리는 단순한 이진 검색 트리의 특수한 경우이기 때문에 이항 검색 트리에 사용되는 작업에서 수정할 필요가 없다.그러나 삽입 또는 제거의 즉각적인 결과는 적색-흑색 나무의 특성을 침해할 수 있으며, 적색-흑색 나무가 자체 균형을 이루도록 복원을 재조정이라고 한다. It requires in the worst case a small number, in Big O notation, where is the number of objects in the tree, on average or amortized , a constant number,[27]: 310 [17]: 158 of color changes (which are very quick in practice); and no more than three tree r오트먼트[28](삽입용 2개)
아래 예시 구현이 적합하지 않은 경우, 벤 파프의 주석이[29] 달린 C 라이브러리 GNU libavl(2019년 6월 기준 v2.0.3)에서 설명이 포함된 다른 구현을 찾을 수 있다.
인서트 및 탈거 작업의 세부 사항은 C++ 코드 예와 함께 시연된다.예제 코드는 아래의 유형 정의와 매크로를 사용하며, 회전에는 도우미 기능을 사용한다.
// 기본 유형 정의: 열거하다 color_t { 블랙, 빨간색 }; 구조상의 RB노드 { // 빨간색-검은색 나무의 노드 RB노드* 부모; // == 트리의 루트가 있는 경우 NULL RB노드* 어린아이의[2]; // == 하위 항목이 비어 있는 경우 NIL // 인덱스: // 왼쪽 := 0인 경우(키 <부모->키) // 오른쪽 :=1, 만일 (키 > 부모->키) 열거하다 color_t 색을 칠하다; 인트로 핵심을; }; #NIL NULL 정의// sentinel 노드에 대한 Null 포인터 또는 포인터 #왼쪽 0도 정의 #오른쪽 1번 정의 #왼쪽 아이를 정의하다[왼쪽] #우아[우아] 정의 구조상의 RB트리 { // 적색-검은색 나무 RB노드* 뿌리를 내리다; // == 트리가 비어 있는 경우 NIL }; // 하위 방향 가져오기({ 왼쪽, 오른쪽} 참조) // NIL이 아닌 비 루트 RBnode* N: #define childDir(N)(N == (N->parent)->오른쪽 ? : 왼쪽 ) RB노드* RotateDirRoot( RB트리* T, // 적색-검은색 나무 RB노드* P, // 뿌리를 내리다 의 하위 계통 (할 수 있다 있다 그 뿌리를 내리다 의 T) 인트로 디르) { // dir ∈ { 왼쪽, 오른쪽 } RB노드* G = P->부모; RB노드* S = P->어린아이의[1-디르]; RB노드* C; 주장하다(S != NIL); // 실제 노드에 대한 포인터가 필요함 C = S->어린아이의[디르]; P->어린아이의[1-디르] = C; 만일 (C != NIL) C->부모 = P; S->어린아이의[ 디르] = P; P->부모 = S; S->부모 = G; 만일 (G != NULL) G->어린아이의[ P == G->맞다 ? 맞다 : 왼쪽 ] = S; 다른 T->뿌리를 내리다 = S; 돌아오다 S; // 하위 트리의 새 루트 } #define RotateDir(N,dir) RotateDirRoot(T,N,dir) #Define RotateLeft(N) RotateDirRoot(T, N, 왼쪽) #Define RotateRight(N) RotateDirRoot(T, N, Right)
삽입 및 제거의 샘플 코드 및 다이어그램에 대한 참고 사항
제안서는 삽입과 제거(일부 매우 간단한 경우는 언급하지 않음)를 모두 6개의 노드와 가장자리, 색상으로 구분하는데, 이를 케이스라고 한다.사례의 코드 수리(재조정)는 때때로 후속 사례의 코드를 사용한다.이 제안서는 삽입과 제거, 정확히 한 검은색 레벨을 뿌리와 루프에 더 가깝게 진화하는 한 가지 경우, 나머지 다섯 가지 경우는 자신의 트리를 재조정하는 내용을 담고 있다.더 복잡한 사건들은 도표로 그려진다.
- 변수
N현재 노드를 나타내며, 다이어그램에 N이라는 레이블이 붙어 있다.  빨간색 노드와 (NIL이 아닌) 검은색 노드(검은색 높이 ≥1)를 기호화하며, NIL 노드가 아닌 노드의 빨간색 또는 검은색이지만 동일한 다이어그램에서 동일한 색상을 나타낸다.NIL 노드는 다이어그램에 표시되지 않는다.
빨간색 노드와 (NIL이 아닌) 검은색 노드(검은색 높이 ≥1)를 기호화하며, NIL 노드가 아닌 노드의 빨간색 또는 검은색이지만 동일한 다이어그램에서 동일한 색상을 나타낸다.NIL 노드는 다이어그램에 표시되지 않는다.- 다이어그램에는 세 개의 열과 두 개에서 네 개의 동작이 포함되어 있다.왼쪽 열은 첫 번째 반복을 나타내고 오른쪽 열은 높은 반복을 나타내며, 가운데 열은 사례를 다른 동작으로 분할하는 것을 나타낸다.[30]
- "엔트리"라는 동작은 사례를 정의하고 대부분의 요구 사항을 위반하는 노드의 색상을 표시한다.
파란색 테두리가 현재 노드 N을 울리고 다른 노드에는 N과의 관계에 따라 레이블이 지정된다. - 회전이 유용하다고 간주되는 경우, 이것은 "회전"이라는 라벨이 붙어 있는 다음 동작에서 그려진다.
- 만약 어떤 기억들이 유용하다고 여겨진다면, 이것은 "색"[31]이라는 라벨이 붙어 있는 다음 동작에서 그려진다.
- 여전히 수리할 필요가 있는 경우, 케이스는 현재 노드 N을 재할당한 후 다른 사례의 코드와 이를 사용하며, 다시 블루 링을 장착하고 다른 노드도 재할당해야 할 수 있다.이 작업은 "재할당"이라는 레이블이 붙어 있다.
삽입과 삭제 둘 다에 대해, 한 가지 경우(정확히) 루트에 더 가까운 하나의 검은색 레벨을 반복한 다음, 재할당된 별자리는 각각의 루프 불변성을 만족한다.
- 검은색 원이 맨 위에 있는 가능한 숫자의 삼각형은 검정색 높이에서 1을 뺀 검정색 높이, 즉 첫 번째 반복에서 0을 뺀 검정색 하위 계수를 나타낸다.그것의 뿌리는 빨갛거나 까맣다.
가능한 숫자의 삼각형은 검은색 높이가 1보다 작은 빨간색-검은색 하위 트리를 나타낸다. 즉, 부모의 높이는 2차 반복에서 검은색이다.
- 비고
- 단순성을 위해 샘플 코드는 다음과 같은 분리를 사용한다.
U == NIL U->color == BLACK // considered black
- 그리고 접속사:
U != NIL && U->color == RED // not considered black
- 따라서 두 진술이 모두 종합 평가되지 않는다는 점을 명심해야 한다.
U == NIL두 경우 모두U->color접촉되지 않음(단락 평가 참조).
(코멘트)considered black요구 사항 2에 따른다.) - 관련자
if-제안이[30] 실현되면 훨씬 덜 자주 발생해야 한다.
삽입
삽입은 새 (NIL이 아닌) 노드를 N이라고 하는 NIL 노드의 이진 검색 트리의 위치에 배치하는 것으로 시작되며, N은 주문 중인 전임자의 키가 새 노드의 키보다 적게 비교되고, 차례로 새 노드의 키보다 적게 비교된다.(이 위치는 종종 바로 앞의 트리 내에서 검색의 결과물이다.)그는 수술을 삽입하고 노드로 구성된다.P방향과 함께dir…과 함께새로 삽입된 노드는 모든 경로에 이전과 동일한 수의 검은색 노드가 포함되도록 일시적으로 빨간색이다.그러나 만약 그것의 부모인 P가 또한 빨강이라면, 이 행동은 적색폭력을 도입한다.
공허하게 하다 RBinsert1( RB트리* T, // -> 적색-흑색 나무 구조상의 RB노드* N, // -> 삽입할 노드 구조상의 RB노드* P, // -> 부모 마디를 짓다 의 N ( 할 수 있다 있다 NULL ) 바이트 디르) // N을 삽입할 위치 P의 측면(왼쪽 또는 오른쪽 ) { 구조상의 RB노드* G; // -> P의 상위 노드 구조상의 RB노드* U; // -> N의 삼촌 N->색을 칠하다 = 빨간색; N->남겨진 = NIL; N->맞다 = NIL; N->부모 = P; 만일 (P == NULL) { // 부모가 없음 T->뿌리를 내리다 = N; // N은 T 나무의 새로운 루트다. 돌아오다; // 삽입 완료 } P->어린아이의[디르] = N; // N을 P의 dir-child로 삽입 // (실행하는 동안) 시작-기울기: 하다 { 리밸런싱 루프는 다음과 같은 불변성을 가진다.
- 현재 노드 N은 각 반복이 시작될 때 (빨간색)이다.
- 요구사항 3은 P가 빨간색일 때(N에서 적색폭력이 발생할 경우) 가능한 예외 N withP와 함께 모든 쌍에 대해 충족된다.
- 다른 모든 속성(요구사항 4 포함)은 트리 전체에서 충족된다.
삽입 다이어그램 참고 사항
| 전에 | 케이스 → | 로타- 티온 | 어시그- 네멘트 | 다음에 | → 다음에 | Δh | ||||||
| P | G | U | x | P | G | U | x | |||||
| — | I3 | → | ||||||||||
| I1 | → | |||||||||||
| — | I4 | → | ||||||||||
| I2 | N:=G | ? | ? | 2 | ||||||||
| i | I5 | P↶N | N:=P | o | I6 | 0 | ||||||
| o | I6 | PgG | → | |||||||||
| 삽입:이 개요는 앞의 열에 모두 나와 있다. 가능한 별자리 케이스가[32] 가려진다. | ||||||||||||
- 도표에서 P는 N의 부모에게, G는 조부모에게, U는 N의 삼촌을 나타낼 것이다.
- 도표는 P가 어느 한 쪽에 있을 수 있음에도 불구하고 부모 노드 P를 부모 G의 왼쪽 자식으로 보여준다.샘플 코드는 측면 변수를 통해 두 가지 가능성을 모두 커버한다.
dir. - N은 삽입 노드지만, 작업이 진행됨에 따라 다른 노드가 최신 상태가 될 수 있다(사례 I2 참조).
- 도표는 P가 빨갛게 된 사례, 즉 적색폭행.
- x 열은 자식 방향의 변화를 나타낸다. 즉, ("외부"의 경우)는 P와 N이 모두 왼쪽 또는 오른쪽 어린이임을 의미하지만, i(내부"의 경우)는 자식 방향이 P에서 N으로 바뀐다는 것을 의미한다.
- 열 그룹이 대소문자를 정의하기 전의 열 그룹. 대소문자에는 이름이 지정되어 있다.따라서 비어 있는 셀의 가능한 값은 무시된다.따라서 I2 사례의 경우 해당 다이어그램에 N의 하위 방향 두 가지 가능성이 모두 수록되어 있지만, 샘플 코드는 N의 하위 방향 두 가지 가능성을 모두 포함한다.
- 시놉시스의 행은 가능한 모든 RB 사례의 적용 범위를 쉽게 이해할 수 있도록 정렬된다.
- 열 회전은 회전이 균형 재조정에 기여하는지 여부를 나타낸다.
- 열 할당은 후속 단계를 입력하기 전에 N의 할당을 보여준다.이는 다른 노드 P, G, U의 재할당을 유발할 수 있다.
- 케이스에 의해 어떤 것이 변경되었다면, 이것은 다음의 칼럼 그룹에 표시된다.
- 화살표 → 다음 열은 이 단계를 통해 재조정이 완료되었음을 나타낸다.다음 열에 정확히 하나의 사례가 결정되면 이 사례가 후속 사례로 제공되며 그렇지 않으면 물음표가 있다.
- 루프는 "사례 1 삽입"과 "사례 2 " 섹션에 포함되어 있는데, 여기서 I2의 경우 재조정 문제가 h= 레벨이 트리에서 더 높게 상승하여 할아버지 G가 새로운 현재 노드 N이 된다.따라서 트리를 수리하는 데는 최대 회 반복이 필요하다(여기서 는 트리의 높이임).단계적 상승 확률은 각 반복에 따라 기하급수적으로 감소하기 때문에 총 재조정 비용은 평균적으로 상각 상각 상각한다.
- 루프 본체에서 케이스 I1이 저절로 빠져나가고 케이스 I4, I6, I5 + I6, I3에 대한 출구 분기가 있다.
- 회전은 I6 및 I5 + I6 – 루프 바깥에서 발생한다.따라서, 최대 두 번의 회전이 일어난다.
케이스 1 삽입
현재 노드의 상위 P는 검은색이기 때문에 요구사항 3은 유지된다.요구사항 4는 루프 불변성에 따라 유지된다.
만일 (P->색을 칠하다 == 블랙) { // Case_I1(P black): 돌아오다; // 삽입 완료 } // 지금부터 P는 빨간색이다. 만일 ((G = P->부모) == NULL) 에 가다 케이스_I4; // P 빨강과 뿌리 // 기타: P 빨강과 G!=NULL 디르 = 차일드디르(P); // 노드 P가 위치한 상위 G의 측면 U = G->어린아이의[1-디르]; // 삼촌 만일 (U == NIL U->색을 칠하다 == 블랙) // 검정색으로 간주됨 에 가다 케이스_I56; // P 레드&&U 블랙 케이스 2 삽입
부모 P와 삼촌 U가 모두 빨간색이면 둘 다 검정색으로 칠할 수 있고 조부모 G는 요구 사항 4를 유지하기 위해 빨간색으로 칠할 수 있다.부모나 삼촌을 통과하는 어떤 길도 조부모를 통과해야 하기 때문에 이들 길의 검은 노드의 수는 변하지 않았다.그러나, 조부모 G는 만약 그것이 빨간 부모를 가지고 있다면, 이제 요건 3을 위반할 수 있다.G에서 N으로 다시 샘플링한 후 루프 불변성이 충족되어 한 검정색 수준(= 2 트리 수준)에서 재조정이 반복될 수 있다.
// Case_I2(P+U 빨간색): P->색을 칠하다 = 블랙; U->색을 칠하다 = 블랙; G->색을 칠하다 = 빨간색; N = G; // 새 현재 노드 // 검은색 1단계 더 높게 반복 // (= 2 트리 수준) } 하는 동안에 ((P = N->부모) != NULL); // (실행하는 동안)-기울기 종료 케이스 3 삽입
삽입 케이스 2는 - }}회 실행되었으며 트리의 전체 높이가 1 증가하여 h. 현재 노드 N은 트리의 (빨간색) 루트로서 모든 RB-속성이 충족된다.
// (실행하는 동안)-루프(Case_I2에서 떨어진 후). // 케이스_I3: N은 뿌리와 빨강이다. 돌아오다; // 삽입 완료 케이스 4 삽입
부모 P는 빨간색이고 뿌리는 빨간색이다.N도 적색이기 때문에 요건 3을 위반한다.그러나 P의 색을 바꾼 후에 트리는 RB 형상을 하고 있다.나무의 검은 높이가 1씩 증가한다.
케이스_I4: // P는 루트 및 레드: P->색을 칠하다 = 블랙; 돌아오다; // 삽입 완료 케이스 5 삽입
부모님 P는 빨간색이지만 삼촌 U는 검은색이다.궁극적인 목표는 부모 노드 P를 조부모 위치로 회전시키는 것이지만, N이 G의 "내부" 손자(즉, N이 G의 오른쪽 자녀 또는 G의 왼쪽 자녀인 경우)인 경우에는 이 방법이 통하지 않는다.P에서 A -rotation은 현재 노드 N과 상위 P의 역할을 전환한다.회전은 N까지의 경로(하위 트리의 경로 2번, 도표 참조)를 추가하고 P까지의 경로(하위트리의 경로 4번)를 제거한다.그러나 P와 N은 모두 적색이기 때문에 요건 4는 보존된다.요건 3은 사례 6에서 복구한다.
케이스_I56: // P 레드 && U 블랙: 만일 (N == P->어린아이의[1-디르]) { // Case_I5(P red &&&U black &&N inner grandhood of G): RotateDir(P,디르); // P는 결코 루트가 아니다. N = P; // 새 현재 노드 P = G->어린아이의[디르]; // N의 새 부모 // Case_로 넘어가다.I6 } 케이스 6 삽입
현재 노드 N은 이제 G(왼쪽 아이의 왼쪽 또는 오른쪽 아이의 오른쪽)의 "외부" 손자임이 확실시된다.이제 -rotate at G, 즉 P를 G 대신 배치하고, P를 N과 G의 부모로 만들고, 이전 자녀 P를 빨간색으로 하는데, 요건 3을 위반하였기 때문이다.P와 G의 색을 바꾼 후에 결과 트리는 요구 사항 3을 만족한다.요구사항 4 또한 만족스러운 것으로, 블랙 G를 거쳤던 모든 경로가 이제 블랙 P를 거치기 때문이다.
// Case_I6 (G의 P red &&& U black &&N 외손자): RotateDirRoot(T,G,1-디르); // G가 루트일 수 있음 P->색을 칠하다 = 블랙; G->색을 칠하다 = 빨간색; 돌아오다; // 삽입 완료 } // RBinsert1의 끝 알고리즘은 보조 데이터 구조를 사용하지 않고, 보조 변수를 위해 소량의 여분의 저장 공간만 사용하여 입력을 변환하기 때문에, 그것은 그 안에 있다.
제거: 간단한 사례
라벨 N은 항목에서 삭제할 노드인 현재 노드를 나타낸다.
N이 NIL이 아닌 자식을 갖지 않은 루트인 경우, N은 NIL 노드로 대체되고, 그 후에 트리가 비어 있고, RB 모양으로 N은 N은 NIL 노드로 대체된다.
N이 NIL이 아닌 두 개의 하위 그룹을 가지고 있는 경우, 왼쪽 하위 트리의 최대 요소(순서 중인 선행 요소) 또는 오른쪽 하위 트리의 최소 요소(순서 중인 후속 요소)에 대한 추가 탐색은 (여기 표시된 대로) 사이에 다른 노드가 없는 노드를 찾는다.R이라고 하는 이 "교체 노드"는 하위 트리의 최대 또는 최소 요소로서 NIL이 아닌 아이 한 명 이상이다.소프트웨어를 사용자가 정의한 노드 구조로부터 완전히 독립적으로 유지하기 위해 N과 R, 즉 두 노드의 색과 포인터와 관련된 모든 적색-흑색 트리 데이터를 교환한다.(수정된 적색-흑색 트리는 N과 R 사이의 역순을 제외하고 이전과 동일하며, N을 제거함으로써 즉시 해결되는 문제) 이제 N은 NIL이 아닌 아이를 기껏해야 한 명 가지고 있다.
만약 N이 NIL이 아닌 아이가 정확히 한 명이라면, 그것은 빨간 아이여야 한다. 왜냐하면 만약 그것이 검은색이라면, 요건 4는 두 번째 검정색 NIL이 아닌 아이를 강제할 것이기 때문이다.
N이 빨간색 노드인 경우, NIL이 아닌 하위 노드를 가질 수 없으며, 이는 요구 사항 3에 따라 검정색이 되어야 하기 때문이다.게다가, 그것은 바로 위에서 주장했던 것처럼 정확히 한 명의 흑인 아이를 가질 수 없다.결과적으로, 빨간색 노드 N은 아이가 없으며 간단히 제거될 수 있다.
N이 검은색 노드인 경우, 빨간색 아이를 가지거나 NIL이 아닌 아이가 전혀 없을 수 있다.N이 빨간 아이를 가지고 있다면, 단순히 후자를 검은색으로 칠한 후 이 아이로 대체된다.
검은색 비루트 잎 제거
복잡한 경우는 N이 뿌리가 아닌 검은색이고 NIL 자식만 있는 경우다.첫 번째 반복에서 N은 NIL로 대체된다.
공허하게 하다 RBdelete2( RB트리* T, // -> 적색-흑색 나무 구조상의 RB노드* N) // -> 삭제할 노드 { 구조상의 RB노드* P = N->부모; // -> N의 상위 노드 바이트 디르; // N이 위치한 P의 측면({ 왼쪽, 오른쪽 } 참조) 구조상의 RB노드* S; // -> N의 형제 구조상의 RB노드* C; // -> 친한 조카 구조상의 RB노드* D; // -> 먼 조카 // P != N은 루트가 아니기 때문에 NULL. 디르 = 차일드디르(N); // 노드 N이 위치한 상위 P의 측면 // 상위 P의 N을 NIL로 대체: P->어린아이의[디르] = NIL; 에 가다 시작_D; // 루프에 뛰어들다 // (실행하는 동안) 시작-기울기: 하다 { 디르 = 차일드디르(N); // 노드 N이 위치한 상위 P의 측면 시작_D: S = P->어린아이의[1-디르]; // N의 형제(검은색 키 >= 1) D = S->어린아이의[1-디르]; // 먼 조카 C = S->어린아이의[ 디르]; // 가까운 조카 만일 (S->색을 칠하다 == 빨간색) 에 가다 케이스_D3; // S 빨강 ===> P+C+D 검정 // S는 검은색: 만일 (D != NIL && D->색을 칠하다 == 빨간색) // 검은색으로 간주되지 않음 에 가다 케이스_D6; // D 레드 && S 블랙 만일 (C != NIL && C->색을 칠하다 == 빨간색) // 검은색으로 간주되지 않음 에 가다 케이스_D5; // C 레드 && S+D 블랙 // 여기 두 조카는 모두 == NIL(첫 번째 반복) 또는 검은색(더 늦음)이다. 만일 (P->색을 칠하다 == 빨간색) 에 가다 케이스_D4; // P 레드 && C+S+D 블랙 리밸런싱 루프는 다음과 같은 불변성을 가진다.
- 각 반복이 시작될 때 검은색 높이 N은 반복 번호에서 1을 뺀 값과 같으며, 이는 첫 번째 반복에서 0이고 N은 더 높은 반복에서 진정한 검은색 노드임을 의미한다.
- N을 통과하는 경로의 블랙 노드 수는 삭제 이전보다 1개 줄어든 반면, 다른 모든 경로에서는 변경되지 않아 다른 경로가 존재할 경우 P에서 블랙 폭력이 발생한다.
- 다른 모든 속성(요구사항 3 포함)은 트리 전체에서 충족된다.
다이어그램 삭제에 대한 참고 사항
| 전에 | 케이스 → | 로타- 티온 | 어시그- 네멘트 | 다음에 | → 다음에 | Δh | ||||||
| P | C | S | D | P | C | S | D | |||||
| — | D2 | → | ||||||||||
| D3 | PHS | N:=N | ? | ? | ? | 0 | ||||||
| D1 | N:=P | ? | ? | 1 | ||||||||
| D4 | → | |||||||||||
| D5 | 씨제스 | N:=N | D6 | 0 | ||||||||
| D6 | PHS | → | ||||||||||
| 삭제:이 개요는 앞의 열에 모두 나와 있다. 가능한 색 별자리 케이스가[32] 가려진다. | ||||||||||||
- In the diagrams below, P is used for N’s parent, S for the sibling of N, C (meaning close nephew) for S’s child in the same direction as N, and D (meaning distant nephew) for S’s other child (S cannot be a NIL node in the first iteration, because it has to have black height one, which was the black height of N before its deletion, but C and D may be NIL 노드).
- 다이어그램은 N이 어느 한 쪽에 있을 수 있음에도 불구하고 현재 노드 N을 부모 P의 왼쪽 자식으로 보여준다.코드 샘플은 측면 변수를 통해 두 가지 가능성을 모두 커버한다.
dir. - 제거 시작(첫 번째 반복에서)에서 N은 삭제할 노드를 대체하는 NIL 노드다.부모 노드의 위치만이 중요하기 때문에 삭제 다이어그램의 왼쪽 열에는 (현재 노드 N은 NIL 노드 및 왼쪽 하위 노드라는 의미)로 상징된다.작업이 진행됨에 따라 적절한 노드(검은색 높이 ≥1)도 최신 상태가 될 수 있다(예: 사례 D1 참조).
- 삭제 다이어그램에서 검정 글머리 기호(
 및 )를 세면 N을 통과하는 경로에 다른 경로보다 한 글머리 기호가 적음을 확인할 수 있다.이것은 P에서의 흑색폭력을 의미한다. 만약 그것이 존재한다면.
및 )를 세면 N을 통과하는 경로에 다른 경로보다 한 글머리 기호가 적음을 확인할 수 있다.이것은 P에서의 흑색폭력을 의미한다. 만약 그것이 존재한다면. - 열 그룹의 색상 별자리는 대소문자를 정의하며, 대소문자에는 이름이 지정된다.따라서 비어 있는 셀의 가능한 값은 무시된다.
- 시놉시스의 행은 가능한 모든 RB 사례의 적용 범위를 쉽게 이해할 수 있도록 정렬된다.
- 열 회전은 회전이 균형 재조정에 기여하는지 여부를 나타낸다.
- 열 할당은 후속 단계를 입력하기 전에 N의 할당을 보여준다.이는 다른 노드 P, C, S, D의 재할당을 유발할 수 있다.
- 케이스에 의해 어떤 것이 변경되었다면, 이것은 다음의 칼럼 그룹에 표시된다.
- 화살표 → 다음 열은 이 단계를 통해 재조정이 완료되었음을 나타낸다.다음 열에 정확히 하나의 사례가 결정되면 이 사례가 후속 사례로 제공되며 그렇지 않으면 물음표가 있다.
- 루프는 다음 섹션에 포함되어 있다.
Start_D"Delete case 1"을 통해, 재조정 문제가 = 1} 트리에서 상위 P가 새로운 현재 노드 N이 되는 경우.따라서 트리를 수리하는 데 최대 번 반복이 필요하다(서 h{\는 트리의 높이임).단계적 상승 확률은 각 반복에 따라 기하급수적으로 감소하기 때문에 총 재조정 비용은 평균적으로 상각 상각 상각한다.(한편으로는 다음과 같다.멜혼앤샌더스는 "AVL 트리는 지속적인 상각 업데이트 비용을 지원하지 않는다"[17]: 165, 158 고 지적한다.이는 삭제 후 재조정하는 경우 해당되지만 AVL 삽입은 해당되지 않는다.)[33] - 루프의 본체에서 케이스 D3, D6, D5 + D6, D4 및 D2로 나가는 지점들이 있다; 섹션 "Delete Case 3"는 케이스 D6, D5 및 D4와 세 개의 다른 기존 지점들이 있다.
- 회전은 사례 D6 및 D5 + D6 및 D3 + D5 + D6에서 모두 루프 밖에서 발생한다.따라서, 최대 세 번의 회전이 일어난다.
사례 1 삭제
P, S, S의 아이들은 흑인이다.S red를 도색한 후, 정확히 N을 통과하지 않는 S를 통과하는 모든 경로는 하나 더 적은 검은색 노드가 있다.이제 P에 의해 루팅된 하위 트리의 모든 경로는 동일한 수의 검은색 노드를 가지고 있지만, P를 통과하지 않는 경로보다 한 개 적기 때문에 요건 4가 여전히 위반될 수 있다.P에서 N으로 다시 샘플링한 후 루프 불변성이 충족되어 한 검정색 수준(=1 트리 수준)에서 재조정이 반복될 수 있다.
// Case_D1(P+C+S+D 검은색): S->색을 칠하다 = 빨간색; N = P; // 새 현재 노드(아마 루트) // 검은색 1레벨 반복 // (= 1 트리 수준) 더 높음 } 하는 동안에 ((P = N->부모) != NULL); // (실행하는 동안)-기울기 종료 사례 2 삭제
현재 노드 N은 새로운 루트다.모든 경로에서 하나의 검은색 노드가 제거되었으므로 RB-속성이 보존된다.나무의 검은 높이는 1만큼 줄어든다.
// Case_D2(P == NULL): 돌아오다; // 삭제 완료 사례 3 삭제
S형제는 빨강색이라 P와 조카 C와 D형은 검정색이어야 한다.P에서의 A -rotation은 S를 N의 조부모로 바꾼다.그리고 나서 P와 S의 색상을 반전시킨 후에도, N을 통과하는 길은 여전히 짧은 하나의 검은 노드가 된다.그러나 N은 빨간색 부모 P와 검정색 형제 S를 가지고 있기 때문에 사례 D4, D5 또는 D6에서의 변환은 RB 형상을 복원할 수 있다.
케이스_D3: // S 레드 && P+C+D 블랙: RotateDirRoot(T,P,디르); // P가 루트일 수 있음 P->색을 칠하다 = 빨간색; S->색을 칠하다 = 블랙; S = C; // != NIL // now: P red&&&S black D = S->어린아이의[1-디르]; // 먼 조카 만일 (D != NIL && D->색을 칠하다 == 빨간색) 에 가다 케이스_D6; // D 레드 && S 블랙 C = S->어린아이의[ 디르]; // 가까운 조카 만일 (C != NIL && C->색을 칠하다 == 빨간색) 에 가다 케이스_D5; // C 레드 && S+D 블랙 // 그렇지 않으면 C+D가 검은색으로 간주된다. // Case_D4로 넘어감 사례 4 삭제
S형제와 S형제의 아이들은 검은색이지만 P형은 빨간색이다.S와 P의 색상을 교환하는 것은 S를 통과하는 경로의 블랙 노드 수에 영향을 미치지 않지만, N을 통과하는 경로의 블랙 노드 수에 1을 더하여 해당 경로에서 삭제된 블랙 노드를 보충한다.
케이스_D4: // P 레드 && S+C+D 블랙: S->색을 칠하다 = 빨간색; P->색을 칠하다 = 블랙; 돌아오다; // 삭제 완료 사례 5 삭제
S형제는 검은색, S형의 가까운 아이 C는 빨간색, S의 먼 아이 D는 검은색이다.S에서의 회전 후 조카 C는 S의 부모, N의 새 동생이 된다.S와 C의 색상은 교환된다.모든 경로에는 여전히 동일한 수의 검은색 노드가 있지만, 현재 N에는 먼 아이가 빨간색인 검정색 형제자매가 있으므로 별자리는 사례 D6에 적합하다. N도 부모 P도 이러한 변환의 영향을 받지 않으며, P도 빨간색이나 검은색(![]() 도표에서)일 수 있다.
도표에서)일 수 있다.
케이스_D5: // C 빨간색 && S+D 검은색: RotateDir(S,1-디르); // S는 결코 루트가 아니다. S->색을 칠하다 = 빨간색; C->색을 칠하다 = 블랙; D = S; S = C; // 지금: D red &&&s black // Case_D6으로 넘어감 사례 6 삭제
S형제는 검은색, S형제의 먼 아이 D는 빨간색이다.P에서 -rotation 후 형제 S는 P와 S의 먼 아이 D의 부모가 된다.P와 S의 색을 교환하고, D를 검정색으로 만든다.하위 트리는 여전히 뿌리에 같은 색, 즉 빨강이나 검정(![]() 도표에서)을 가지고 있는데, 이는 변환 전과 후 모두 같은 색상을 가리킨다.이 방법의 요건 3은 보존된다.N을 통과하지 않는 하위 트리의 경로(도표에서 D와 노드 3을 통과하는 i.o.w.)는 이전과 동일한 수의 검은색 노드를 통과하지만, N은 이제 P가 검은색이 되었거나, 아니면 검은색이었고 S가 흑인 조부모로 추가되었다.따라서 N을 통과하는 경로는 1개의 추가 검은색 노드를 통과하므로 요건 4가 복원되고 전체 트리가 RB 형으로 표시된다.
도표에서)을 가지고 있는데, 이는 변환 전과 후 모두 같은 색상을 가리킨다.이 방법의 요건 3은 보존된다.N을 통과하지 않는 하위 트리의 경로(도표에서 D와 노드 3을 통과하는 i.o.w.)는 이전과 동일한 수의 검은색 노드를 통과하지만, N은 이제 P가 검은색이 되었거나, 아니면 검은색이었고 S가 흑인 조부모로 추가되었다.따라서 N을 통과하는 경로는 1개의 추가 검은색 노드를 통과하므로 요건 4가 복원되고 전체 트리가 RB 형으로 표시된다.
케이스_D6: // D 레드 && S 블랙: RotateDirRoot(T,P,디르); // P가 루트일 수 있음 S->색을 칠하다 = P->색을 칠하다; P->색을 칠하다 = 블랙; D->색을 칠하다 = 블랙; 돌아오다; // 삭제 완료 } // RBdelete2의 끝 알고리즘은 보조 데이터 구조를 사용하지 않고, 보조 변수를 위해 소량의 여분의 저장 공간만 사용하여 입력을 변환하기 때문에, 그것은 그 안에 있다.
경계 증명
의 경우 높이 의 빨간색-검은색 트리가 있다.
(플로어 기능 포함 경우
노드 및 노드가 더 적은 이 트리 높이의 빨간색-검은색 트리는 없다. 따라서 최소화된 것이다.
검은색 높이는 ⌈ / (검은색 루트 포함) 또는 홀수 (당시 빨간색 루트 포함) (- )/ . 이다.
- 증명
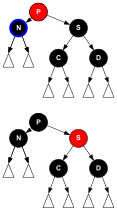
특정 높이의 적색-흑색 트리가 최소의 노드 수를 가지려면 최소 흑색 높이로 최대 적색 노드 수를 가진 하나의 긴 경로를 정확히 가져야 한다.이 경로 외에 다른 모든 노드는 검은색이어야 한다.[16]: 444 Proof sketch 노드가 이 트리에서 분리되면 높이가 손실되거나 RB 속성이 손실된다.
빨간색 루트가 있는 높이 = 의 RB 트리는 최소값이다.이것은 와 일치한다.
높이 > 의 최소 RB 트리(그림 4의 RBh)는 두 자식 하위 트리의 키가 다른 루트를 가지고 있다.The higher child subtree is also a minimal RB tree, RBh–1, containing also a longest path that defines its height ; it has nodes and the black height The other subtree is a perfect binary tree of (black) height having black nodes—and no red node.그러면 노드 수는 유도에 의한 것이다.
| (하위 하위 트리) | (뿌리) | (두 번째 하위 트리) | ||||||||
| 결과적으로 | ||||||||||
| / + (h+ )/ - { - 2 {\ h }-2 ■ | ||||||||||
The graph of the function is convex and piecewise linear with breakpoints at where The function has been tabulated as 에 대한 A027383(h–1)(OEIS에서 순차 A027383).
- 에 대한 기능 해결
> = 3 2^{은는 > 2 3 / 2 {\ 3}}으로 이어지고 홀수 에 대해서는 이(가) 다음과 같이 된다.
- .
따라서 홀수 사례뿐만 아니라 짝수 사례에서도 이(가) 간격 내에 있음
| (완벽한 이진 트리) | (빨간색-검은색 나무) |
이(가) 노드 수입니다.[34]
- 결론
노드(키)가 있는 빨간색-검은 트리 높이 ∈ 로그 ). n)를 갖는다
작업 및 대량 작업 설정
단일 요소 삽입, 삭제 및 조회 작업 외에도 적색-흑색 트리에 조합, 교차로, 설정 차이 등 여러 설정 작업이 정의되었다.그런 다음 이러한 설정 함수에 따라 삽입 또는 삭제에 대한 빠른 대량 작업이 구현될 수 있다.이러한 설정 작업은 분할 및 결합이라는 두 가지 도우미 작업에 의존한다.새로운 운영으로, 적색-흑색 나무의 구현은 더 효율적이고 매우 평행할 수 있다.[35]시간 복잡성을 달성하기 위해 이 구현은 뿌리가 빨간색 또는 검은색일 수 있도록 허용되고 모든 노드가 자신의 검은 높이를 저장하도록 요구한다.
- 조인: 조인 기능은 두 개의 적색-검은색 t와1 t와2 키 k에 있는데, 여기서 t1 < k < t2, 즉 t의1 모든 키가 k 미만이고 t의2 모든 키가 k보다 크다.그것은 k뿐만 아니라 t1, t의2 모든 원소를 포함하는 트리를 반환한다.
- 두 나무의 높이가 같은 검은색이면 조인(Join)은 단순히 왼쪽 하위 트리 t1, 루트 k, 오른쪽2 하위 트리 t로 새 노드를 만든다.t와1 t2 둘 다 검은 루트가 있는 경우 k를 빨간색으로 설정한다.그렇지 않으면 k는 검은색으로 설정된다.
- 검은색 높이가 동일하지 않으면1 t가 t보다2 큰 검은색 높이를 가졌다고 가정한다(다른 경우는 대칭).조인(Join2)은 t와 균형을 이루는 검정 노드 c까지 t의1 오른쪽 척추를 따른다.이때 왼쪽 child c, 루트 k(빨간색으로 설정) 및 오른쪽 child t가2 있는 새로운 노드가 생성되어 c를 대체한다.새 노드는 빨간색-검은색 불변성을 무효화할 수 있다. 왜냐하면 빨간색 노드는 3개까지 연속으로 나타날 수 있기 때문이다.이것은 이중 회전으로 고칠 수 있다.이중 적색 문제가 루트로 전파되면 루트는 검은색으로 설정되어 속성을 복원한다.이 기능의 비용은 두 입력 트리 사이의 검은색 높이 차이다.
- 분할: 적색-검은색 나무를 키 x보다 작은 나무와 키 x보다 큰 나무 두 그루로 분할하려면 먼저 적색-검은 나무에 x를 삽입하여 뿌리부터 경로를 그린다.이 삽입 후 경로 왼쪽에서 x보다 작은 값을 모두 찾으며, 오른쪽에서 x보다 큰 값을 모두 찾는다.조인을 적용하면 왼쪽의 모든 하위 트리가 아래쪽부터 위쪽까지의 중간 노드로 경로의 키를 사용하여 상향식 통합되고 오른쪽 부분은 대칭이다.
- 일부 응용 프로그램의 경우 분할은 x가 트리에 나타날 경우 나타내는 부울 값도 반환한다.분할 비용은 트리 높이의 ), O n순이다.이 알고리즘은 실제로 빨간색-검은색 트리의 어떤 특별한 특성과도 무관하며, AVL 트리와 같이 결합 연산이 있는 트리에 사용될 수 있다.
조인 알고리즘은 다음과 같다.
function joinRightRB(TL, k, TR): if (TL.color=black) and (TL.blackHeight=TR.blackHeight): return Node(TL,⟨k,red⟩,TR) T'=Node(TL.left,⟨TL.key,TL.color⟩,joinRightRB(TL.right,k,TR)) if (TL.color=black) and (T'.right.color=T'.right.right.color=red:T'.right.right.color=black; return Left(T') return T' /* t't'[rete T'] */ function LeftRB(TL, k, TR): /* 대칭으로 RightRB */ funnight(TLL, K, TR): 만약R T.blackheight:T'=joinRightRBL(T,kR,T) if (T'.color=red) 및 (T'.right.color=red):TR'.color=blackhight>TL.blackHight: /* 대칭 */ if (TL.color=black) 및 (TR.color=black): 반환 노드(TL, ⟨k, red⟩, TR) 반환 노드(TL, ⟨k, black⟩, tR)
분할 알고리즘은 다음과 같다.
function split(T, k): if (T = nil) return (nil, false, nil) if (k = T.key) return (T.left, true, T.right) if (k < T.key): (L',b,R') = split(T.left, k) return (L',b,join(R',T.key,T.right)) (L',b,R') = split(T.right, k) return (join(T.left,T.key,L'),b,T.right)
세트 A와 B를 나타내는 두 개의 적색-검은색1 t와2 t의 결합은 A b B를 나타내는 적색-검은색 t이다.다음과 같은 재귀 함수는 이 결합을 계산한다.
함수 유니언(t1, t2): t12 = nil 반환21 t(L,b1,R1)=split(t1,t2.key) proc1=start인 경우:TL=union(L1,t2.left) proc2=start:TR=union(R1,t2.right) 모든 proc1,proc2 리턴 조인(TL, t2.key, TR) 대기
여기서, 분할은 두 개의 나무를 돌려주는 것으로 추정된다. 하나는 키를 덜 쥐고 있고, 다른 하나는 더 큰 키를 쥐고 있다.(알고리즘은 비파괴적이지만, 내부 파괴 버전도 존재한다.)
교차점이나 차이에 대한 알고리즘은 유사하지만 조인(Join)과 동일하지만 중간 키가 없는 조인2 도우미 루틴이 필요하다.조합, 교차로 또는 차이에 대한 새로운 기능에 기초하여 하나의 키 또는 복수의 키를 적색-흑색 트리에 삽입하거나 삭제할 수 있다.스플릿은 조인(Join)을 호출하지만 적색-흑색 나무의 균형 기준을 직접 다루지 않기 때문에, 이러한 구현을 보통 "조인 기반" 구현이라고 부른다.
, 교차로 및 차이의 복잡도는 m 과와) 와 크기의 적색-흑색 나무 두 그루에 대해 \ m이다이 복잡성은 비교 횟수에 있어서 최적이다.이후 노조, 교차로 또는 차이에 반복적인 호출은 서로 독립적이다 더욱 중요한 것은, 그들은 병렬로 언제 m=1{\displaystyle m=1}O{O(m\log n\log)\displaystyle}.[35](로그 m로그 n)는 평행하는 깊이를 실행할 수 있으면join-based 구현은 같은 computational 원자가 비고리형인그램을 감독했다.aph(DAG) 작은 트리를 분할하는 데 큰 트리의 루트를 사용하는 경우 단일 요소 삽입 및 삭제로 한다.
병렬 알고리즘
정렬된 항목 목록에서 적색-흑색 트리를 구성하기 위한 병렬 알고리즘은 컴퓨터 모델에 따라 사용 가능한 수가 →】 항목의 n 수에 무증상적으로 비례하는 경우, O) O n시간에 실행될 수 있다. 빠른 검색, 삽입, 삭제 병렬 알고리즘도 알려져 있다.[36]
적색-흑색 나무의 결합 기반 알고리즘은 조합, 교차로, 건설, 필터, 지도 축소 등을 포함한 대량 작업에서 평행하다.
병렬 대량 작업
삽입, 제거 또는 업데이트와 같은 기본 작업은 여러 요소의 돌출부를 처리하는 작업을 정의하여 병렬화할 수 있다.또한 몇 가지 기본 연산을 통해 불룩을 처리하는 것도 가능하다. 예를 들어 불룩은 삽입할 요소와 트리로부터 제거할 요소도 포함할 수 있다.
대량 작업을 위한 알고리즘은 적색-흑색 트리에만 적용되는 것이 아니라 2-3 트리, 2-3-4 트리, (a,b)-트리처럼 정렬된 다른 시퀀스 데이터 구조에도 적용할 수 있다.다음의 대량 삽입 알고리즘에서는 설명하겠지만, 제거와 업데이트에도 동일한 알고리즘을 적용할 수 있다.대량 삽입은 시퀀스 의 각 요소를 T 에 삽입하는 작업이다
가입 기반
이 접근방식은 효율적인 결합 및 분할 연산을 지원하는 모든 정렬된 시퀀스 데이터 구조에 적용할 수 있다.[37]일반적인 아이디어는 과 을(를) 여러 부분으로 나누고 이들 부분에 삽입을 병렬로 수행하는 것이다.
- 먼저 삽입할 요소의 대량 I을(를) 정렬해야 한다.
- 그 후 알고리즘은 을(를) N+ 부분 I , k 로 분할한다.
- Next the tree has to be split into parts in a way, so that for every following constraints hold:
- 이제 알고리즘은 의 각 요소를 에 순차적으로 삽입한다.이 단계는 모든 에 대해 수행되어야 하며 최대 프로세서가 병렬로 수행할 수 있다.
- 마지막으로 결과수목들이 합류하여 전체 수술의 최종 결과를 형성하게 된다.
3단계에서 을 분할하기 위한 제약 {\displaystyle 은(는) 5단계에서 트리를 다시 결합하고 결과 시퀀스를 정렬할 수 있음을 보장한다는 점에 유의하십시오
의사 코드는 대량 삽입을 위한 조인 기반 알고리즘의 단순한 분할 및 커커 구현을 보여준다.두 재귀 호출은 병렬로 실행할 수 있다.여기서 사용되는 조인 연산은 이 기사에서 설명하는 버전과 다르며, 대신 조인2가 사용되어 두 번째 매개 변수 k를 놓친다.
bulkInsert(T, I, k): I.sort() bulklInsertRec(T, I, k) bulkInsertRec(T, I, k): if k = 1: forall e in I: T.insert(e) else m := ⌊size(I) / 2⌋ (T1, _, T2) := split(T, I[m]) bulkInsertRec(T1, I[0 .. m], ⌈k / 2⌉) bulkInsertRec(T2, I[m + 1 .. size(I) - 1], ⌊k / 2⌋) T ← join2(T1, T2)
실행시간
{\ I} 이 분석에서 고려되지 않는다
| #재발 수준 | |
| T(분할) + T(조인) | |
| 나사산당 삽입 | |
| T(삽입) | |
| 이(가) 있는 T(bulkInsert) = #processor |
이것은 분할과 결합에 병렬 알고리즘을 사용함으로써 개선될 수 있다.이 경우 실행 시간은 + I T ) T T \right 입니다[38]
일
| #오직, #오직 | |
| W(분할) + W(조인) | |
| #삽입 | |
| W(삽입) | |
| W(bulkInsert) |
파이프라이닝
대량 작업을 병렬화하는 또 다른 방법은 파이프라인 방식을 사용하는 것이다.[39]이것은 기본적인 조작을 일련의 하위 작업으로 처리하는 작업을 세분화함으로써 이루어질 수 있다.여러 기본 작업의 경우 각 하위 작업을 별도의 프로세서에 할당하여 하위 작업을 병렬로 처리할 수 있다.
- 먼저 삽입할 요소의 대량 I을(를) 정렬해야 한다.
- 의 각 요소에 대해 알고리즘은 T 의 삽입 위치에 따라 위치한다 이 에서 T 은(는) 변경되지 않으므로 각 요소 for I에 대해 병렬로 수행할 수 있다.이제 은(는) 각 요소의 삽입 위치에 S S로 분할되어야 한다.예를 들어 s , e 은(는) 노드 의 왼쪽에 삽입 위치가 있는 요소를 포함하는 의 반복성이다
- 모든 {\의 중간 m, d 이(가) 노드 에 삽입된다이것은 각 , r 의 삽입 위치가 정의상 고유하므로 각 m , d i m_{에 대해 병렬로 수행할 수 있다.If contains elements to the left or to the right of , those will be contained in a new set of subsequences as or ,
- 이제 은(는) 경로 끝에 최대 2개의 연속적인 빨간 노드를 포함할 수 있으며, 이 노드는 수리가 필요하다.수리하는 동안 해당 노드가 회전 영향을 받는 경우 S 요소의 삽입 위치를 업데이트해야 한다는 점에 유의하십시오.
두 개의 노드가 가장 가까운 흑인 조상이 서로 다를 경우 병렬로 수리할 수 있다.최대 4개의 노드에서 동일한 가장 가까운 검은색 조상을 가질 수 있으므로, 가장 낮은 수준의 노드는 일정한 수의 병렬 스텝으로 수리할 수 있다.
이 단계는 이(가) 완전히 수리될 때까지 위의 검은색 수준에 연속적으로 적용된다. - 부터 5단계까지는 S S이(가) 비어 있을 때까지 새로운 반복에서 반복된다.이때 모든 요소 I 이(가) 삽입되었다.이 단계들의 각각의 적용은 스테이지라고 불린다. 의 부분 길이는 O( I) O ( 이고, 모든 단계에서 부분 부분적인 부분들은 are O ( 로그 ) O I )}이다
모든 단계가 나무의 검은 층으로 올라가기 때문에, 그것들은 파이프라인에서 평행해질 수 있다.한 스테이지가 한 검정 레벨의 처리를 마치면, 다음 스테이지가 그 레벨에서 위로 올라가 계속할 수 있다.
실행시간
{\ I} 이 분석에서 고려되지 않는다또한 I이(가) T보다 작은 것으로 가정하고 그렇지 않으면 결과 트리를 처음부터 구성하는 것이 더 효율적일 것이다.
| T(삽입 위치 찾기) | |
| #stages | |
| T(삽입) + T(수리) | |
| ~ #프로세서가 있는 T(bulkInsert) |
일
| W(삽입 위치 찾기) | |
| #삽입, #장식 | |
| W(삽입) + W(수리) | |
| W(bulkInsert) |
대중문화
Robert Sedgewick이 강의 중 하나에서 언급한 바와 같이, 빨간색-검은색 트리가 Missing의[40] 에피소드에서 정확하게 언급되었다.[41]
제스
: 다시빨간 문이었다.
폴록:빨간 문이 창고인 줄 알았어.
제스:하지만 그것
은 더이상 빨간색
이 아니라검은색이었어.
안토니오:그래서 빨간색이 검은색으로 바뀐다는 것은 무엇을 의미하는가?
폴록:예산 적자, 적색 잉크, 흑색 잉크.
안토니오:바이너리 검색 트리에서 나온 것일 수도 있다.
빨간색-검은색 트리는 한 노드에서 동일한 수의 검은색 노드를 가진 하위 잎까지의 모든 간단한 경로를 추적한다.
제스:그게 여자들한테 도움이 돼?
참고 항목
- 데이터 구조 목록
- 트리 데이터 구조
- 나무 회전
- AA 나무, 적색-흑색 나무의 변형
- AVL 트리
- B-트리(2–3 트리, 2–3–4 트리, B+ 트리, B*-트리, UB-트리)
- 희생양나무
- 스플레이 트리
- T-트리
- WAVL 트리
참조 및 참고 사항
- ^ a b c d James Paton. "Red–Black Trees".
- ^ a b 균형만 재조정(조회 없음), 타르잔과 멜혼을 보라.
- ^ a b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Red–Black Trees". Introduction to Algorithms (second ed.). MIT Press. pp. 273–301. ISBN 978-0-262-03293-3.
- ^ Morris, John (1998). "Red–Black Trees". Data Structures and Algorithms.
- ^ Rudolf Bayer (1972). "Symmetric binary B-Trees: Data structure and maintenance algorithms". Acta Informatica. 1 (4): 290–306. doi:10.1007/BF00289509. S2CID 28836825.
- ^ Drozdek, Adam (2001). Data Structures and Algorithms in Java (2 ed.). Sams Publishing. p. 323. ISBN 978-0534376680.
- ^ a b Leonidas J. Guibas and Robert Sedgewick (1978). "A Dichromatic Framework for Balanced Trees". Proceedings of the 19th Annual Symposium on Foundations of Computer Science. pp. 8–21. doi:10.1109/SFCS.1978.3.
- ^ "Red Black Trees". eternallyconfuzzled.com. Archived from the original on 2007-09-27. Retrieved 2015-09-02.
- ^ Robert Sedgewick (2012). Red–Black BSTs. Coursera.
A lot of people ask why did we use the name red–black. Well, we invented this data structure, this way of looking at balanced trees, at Xerox PARC that was the home of the personal computer and many other innovations that we live with today entering[sic] graphic user interfaces, ethernet and object-oriented programmings[sic] and many other things. But one of the things that was invented there was laser printing and we were very excited to have nearby color laser printer that could print things out in color and out of the colors the red looked the best. So, that’s why we picked the color red to distinguish red links, the types of links, in three nodes. So, that’s an answer to the question for people that have been asking.
- ^ "Where does the term "Red/Black Tree" come from?". programmers.stackexchange.com. Retrieved 2015-09-02.
- ^ Andersson, Arne (1993-08-11). "Balanced search trees made simple". In Dehne, Frank; Sack, Jörg-Rüdiger; Santoro, Nicola; Whitesides, Sue (eds.). Algorithms and Data Structures (Proceedings). Lecture Notes in Computer Science. Vol. 709. Springer-Verlag Berlin Heidelberg. pp. 60–71. CiteSeerX 10.1.1.118.6192. doi:10.1007/3-540-57155-8_236. ISBN 978-3-540-57155-1. Archived from the original on 2018-12-08. Alt URL
- ^ Okasaki, Chris (1999-01-01). "Red–black trees in a functional setting". Journal of Functional Programming. 9 (4): 471–477. doi:10.1017/S0956796899003494. ISSN 1469-7653. Archived from the original (PS) on 2007-09-26. Retrieved 2007-05-13.
- ^ Sedgewick, Robert (1983). Algorithms (1st ed.). Addison-Wesley. ISBN 978-0-201-06672-2.
- ^ Sedgewick, Robert; Wayne, Kevin. "RedBlackBST.java". algs4.cs.princeton.edu. Retrieved 7 April 2018.
- ^ Sedgewick, Robert (2008). "Left-leaning Red–Black Trees".
- ^ a b c Sedgewick, Robert; Wayne, Kevin (2011). Algorithms (4th ed.). Addison-Wesley Professional. ISBN 978-0-321-57351-3.
- ^ a b c d Mehlhorn, Kurt; Sanders, Peter (2008). "7. Sorted Sequences" (PDF). Algorithms and Data Structures: The Basic Toolbox. Berlin/Heidelberg: Springer. CiteSeerX 10.1.1.148.2305. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
- ^ a b Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2009). "13. Red–Black Trees". Introduction to Algorithms (3rd ed.). MIT Press. pp. 308–309. ISBN 978-0-262-03384-8.
- ^ Knuth의 순서 정의 사용: 최대 자녀 수
- ^ Sedgewick, Robert (1998). Algorithms in C++. Addison-Wesley Professional. pp. 565–575. ISBN 978-0-201-35088-3.
- ^ "The Implementation of epoll (1)". September 2014.
- ^ 파프 2004
- ^ a b "Robert Sedgewick" (PDF). Cs.princeton.edu. Retrieved 26 March 2022.
- ^ "Balanced Trees" (PDF). Cs.princeton.edu. Retrieved 26 March 2022.
- ^ Demaine, E. D.; Harmon, D.; Iacono, J.; Pătraşcu, M. (2007). "Dynamic Optimality—Almost" (PDF). SIAM Journal on Computing. 37 (1): 240. doi:10.1137/S0097539705447347. S2CID 1480961.
- ^ "How does a HashMap work in JAVA". coding-geek.com.
- ^ Tarjan, Robert Endre (April 1985). "Amortized Computational Complexity" (PDF). SIAM Journal on Algebraic and Discrete Methods. 6 (2): 306–318. doi:10.1137/0606031.
- ^ 이러한 나무 회전의 중요한 점은 나무 노드의 순서 순서를 보존한다는 것이다.
- ^ "Ben Pfaff (2007): Online HTML version of a well-documented collection of binary search tree and balanced tree library routines".
- ^ a b 왼쪽 열에는 특히 제거를 위해 오른쪽 열보다 훨씬 적은 노드가 포함되어 있다.이는 명명된 노드 중 상당수가 첫 번째 반복에서 NIL 노드이고 나중에 확실히 NIL이 아닌 노드이기 때문에 삽입 및 삭제의 리밸런싱 루프에서 첫 번째 반복을 당겨서 어느 정도 효율성을 얻을 수 있음을 나타낸다.(이 발언도 참조)
- ^ 명확한 이유로 회전이 기억되기 전에 놓여졌다.그러나 두 사람은 통근하기 때문에 자유롭게 꼬리로 회전을 이동시킬 수 있다.
- ^ a b 벤 파프에서도 같은 칸막이를 찾을 수 있다.
- ^ 디네시 P.Mehta, Sartarj Sani (Ed.) 데이터 구조 및 애플리케이션 핸드북 10.4.2
- ^ 상단의 균등성은 짝수 2 k 2k}의 최소 RB2k 트리에 대해 유지되며, = 2k - {\}-2 노드에 대해서만 유지된다.따라서 불평등은 코멘 페이지 264에서와 같이 널리 퍼져 h< 2 (+ 1), )보다 약간 더 정밀하다
게다가, 이 나무들은 RB 요구 조건 1~4에 부합하는 한 가지 색상과 한 가지 색상만 허용하는 이진수다.그러나 어린이를 검은 잎에 붙이는 것과 같은 그러한 나무들이 더 있다. (홀수 키의 최소 RB 트리는 빨간 색에서 검은 색으로 뿌리의 색을 바꿀 수 있다.) - ^ a b Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just Join for Parallel Ordered Sets" (PDF), Symposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Parallel Algorithms and Architectures (SPAA 2016), ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.
- ^ Park, Heejin; Park, Kunsoo (2001). "Parallel algorithms for red–black trees". Theoretical Computer Science. 262 (1–2): 415–435. doi:10.1016/S0304-3975(00)00287-5.
Our parallel algorithm for constructing a red–black tree from a sorted list of items runs in time with processors on the CRCW PRAM and runs in time with processors on the EREW PRAM.
- ^ Sanders, Peter (2019). Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (eds.). Sequential and Parallel Algorithms and Data Structures : The Basic Toolbox. Springer eBooks. Cham: Springer. pp. 252–253. doi:10.1007/978-3-030-25209-0. ISBN 9783030252090. S2CID 201692657.
- ^ Akhremtsev, Yaroslav; Sanders, Peter (2016). "Fast Parallel Operations on Search Trees". HiPC 2016, the 23rd IEEE International Conference on High Performance Computing, Data, and Analytics, Hyderabad, India, December, 19-22. IEEE, Piscataway (NJ): 291–300. arXiv:1510.05433. Bibcode:2015arXiv151005433A. ISBN 978-1-5090-5411-4.
- ^ Jájá, Joseph (1992). An introduction to parallel algorithms. Reading, Mass. [u.a.]: Addison-Wesley. pp. 65–70. ISBN 0201548569.
- ^ Missing (Canadian TV series). A, W Network (Canada); Lifetime (United States).
- ^ Robert Sedgewick (2012). B-Trees. Coursera. 10:37 minutes in.
So not only is there some excitement in that dialogue but it’s also technically correct that you don’t often find with math in popular culture of computer science. A red–black tree tracks every simple path from a node to a descendant leaf with the same number of black nodes they got that right.
추가 읽기
- 수학 세계: 빨간색-검은색
- 샌디에이고 주립 대학교: CS 660: Roger Whitney의 Red-Black 트리 노트
- Pfaff, Ben (June 2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.
외부 링크
- Ben Paff: Binary Search Tree와 Balance Tree에 대한 소개.무료 소프트웨어 재단, Boston 2004, ftp.gnu.org (PDF gzip; 1662 kB)
- 빨간색-검은색 나무 구현(C)
- C에서 완전하고 효과적인 구현
- OCW MIT 교수 강연 붉은 검은 나무의 에릭 데메인
- YouTube의 바이너리 검색 트리 삽입 시각화 – 기본 바이너리 검색 트리 및 왼쪽 편향 적색-흑색 트리에서의 랜덤 및 사전 정렬 데이터 삽입 시각화
- C++로 쓰여진 침입식 적색-검은색 나무
- 3.3 균형 탐색 트리의 적색-흑색 BST
- 빨간색-검은색 BST 데모
- Isabelle에서 검증된 기능 구현(증빙 보조):기능 알고리즘 8장, 확인됨!



 (는) 항목 수입니다.트리 재배열 및 회수 작업과 함께 삽입 및 삭제 작업도 O
(는) 항목 수입니다.트리 재배열 및 회수 작업과 함께 삽입 및 삭제 작업도 O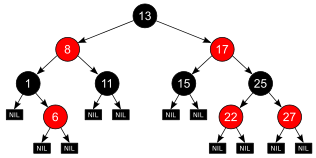




 m
m  충돌 해시코드가 있는 요소의 수입니다.
충돌 해시코드가 있는 요소의 수입니다.


















































![{\displaystyle {\bigl [}<2\log _{2}(n+1)\;{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0c1043c587524d2a645896481b77387cb1ca96e)






 삽입하는 작업이다
삽입하는 작업이다








 순차적으로 삽입한다.이 단계는 모든
순차적으로 삽입한다.이 단계는 모든 















 중간
중간 



























