이항 힙

컴퓨터 과학에서 이항 힙은 우선 큐로 작동하지만 힙 쌍을 병합할 수 있는 데이터 구조입니다.이는 병합 작업을 지원하는 priority 큐인 병합 가능한 힙 추상 데이터 유형(일명 멜더블 힙)의 구현으로 중요합니다.이는 바이너리 힙과 비슷하지만 바이너리 ^[1]힙이 사용하는 완전한 바이너리 트리와는 다른 특수한 트리 구조를 사용하여 구현됩니다.이항 힙은 1978년 장 비유민에 ^[1]^[2]의해 발명되었다.

이항 힙

이항 힙은 다음과 같이 ^[1]재귀적으로 정의되는 이항 트리 집합(단일 이진 트리 모양을 가진 이진 힙과 비교)으로 구현됩니다.

순서 0의 이항 트리는 단일 노드입니다.
$순서$ $k의$ 이항 트리(\ $displaystyle$ k $)$ 에는 $k$ 루트 노드가 있으며, 이 루트 노드는 순서 $k-1$ k - $k-1$ (\ $displaystyle k-1$ $k-2$ - $k-2$ (\ $displaystyle k-2$ ..., 2, 1, 0(이 순서대로)의 이항 트리의 루트입니다.

순서 0 ~ 3의 이항 트리: 각 트리에는 하위 이항 트리의 하위 트리가 강조 표시된 루트 노드가 있습니다.예를 들어, 3차 이항 트리는 2, 1, 0차(각각 파란색, 녹색 및 빨간색으로 강조 표시됨) 이항 트리에 연결됩니다.

$k$ k의이항 트리에는 $노드$ $($ $표시$ $스타일$ 2 $^{$ k} $개$ $)$ 와 $높이$ k(표시 $2^{k}$ $스타일$ k $k$ 가 있습니다.이 이름은 모양에서 유래했습니다 $.k$ \ $k$ k의 이항 트리에는 ${\tbinom {k}{d}}$ $displaystyle$ d에 (k $displaystyle$ ${\tbinom {k}{d}}$ { $d})$ 의 ${\tbinom {k}{d}}$ 노드가 있습니다 ${\tbinom {k}{d}}$ 이 구조상 k ${displaystyle$ k $}$ 의 $k$ 이항 트리는 $k-1$ { $displaystyle$ k-1 $}$ 의 $k-1$ 2개의 트리로 구성되며, 그 중 하나는 다른 트리의 뿌리의 가장 왼쪽 자식으로 부착됩니다.이 기능은 이항 힙의 병합 작업에 중심적이며, 이는 다른 기존 ^[1]^[3]힙에 비해 가장 큰 장점입니다.

이항 힙의 구조

이항 힙은 이항 힙 ^[1]속성을 충족하는 이항 트리 집합으로 구현됩니다.

힙 내의 각 이항 트리는 최소 히프속성에 준거합니다.노드 키는 부모 키보다 크거나 같습니다.
각 순서에는 0차수를 포함하여 이항 트리가 하나만 있을 수 있습니다.

첫 번째 속성은 각 이항 트리의 루트에 트리에서 가장 작은 키가 포함되도록 합니다.따라서 힙 전체에서 가장 작은 키가 루트 ^[1]중 하나입니다.

두 번째 속성은n개의 $노드$ 를 $n$ $가진$ 이항 힙이 최대 $1+\log _{2}n$ + $1+\log _{2}n$ 2 $1+\log _{2}n$ \ $displaystyle$ 1 + \ $log$ _ { $2}n$ 이항 트리로 구성됨을 의미합니다. $\log _{2}$ 서 $\log _{2}$ 2 \ $displaystyle$ \ $log$ _ { $2}}$ 은 $\log _{2}$ 이진 로그입니다.이러한 트리의 수와 순서는 $노드$ 수 n ${displaystyle$ n $n$ $숫자$ n{ $displaystyle$ n $n$ 의 바이너리 표현에서 0이 아닌 비트마다 1개의 이항 트리가 있습니다.예를 들어, 10진수 13은 $2^{3}+2^{2}+2^{0}$ ( $2^{3}+2^{2}+2^{0}$ 2)+ $({$ 2 $^3}+2^{2}+2$ }+2)+ $2^{3}+2^{2}+2^{0}$ 입니다. $^{0$ 따라서 13개의 노드를 가진 이항 힙은 순서 3, 2, 0의 3개의 이항 트리로 구성됩니다(아래 ^[1]^[3]그림 참조).

고유 키를 가진 13개의 노드를 포함하는 이항 힙의 예.
힙은 순서가 0, 2, 3인 3개의 이항 트리로 구성됩니다.

고유한 키를 가진n개의 \ $display$ n개의 $n$ 항목을 이항 힙으로 배열할 수 있는 $n$ 한 방법은 n $!\display n$ 의 $최대$ 홀수입니다 $.$ n $n=1,2,3,\dots$ , $n=1,2,3,\dots$ , $n=1,2,3,\dots$ , $n=1,2,3,\dots$ \ $display style$ n $=$ 1, 2, 3 $,$ $\display$ n }의 $경우 이러한$ 숫자는 $n=1,2,3,\dots$ $n=1,2,3,\dots$ 과 같습니다 $.$

1, 1, 3, 3, 15, 45, 315, 315, 2835, 14175, ...(OEIS의 시퀀스 A049606)

$n$ 의\ $displaystyle$ n개의 $n$ 항목을 이항 힙에 균등하게 랜덤 순서로 삽입하면 각 배열이 동일하게 ^[3]됩니다.

실행

이항 트리의 루트 노드에 대한 랜덤 액세스를 필요로 하는 연산은 없으므로 이항 트리의 루트는 트리의 순서를 늘려 링크된 목록에 저장될 수 있습니다.각 노드의 자녀 수는 가변적이기 때문에 바이너리 트리에서 흔히 볼 수 있는 것처럼 각 노드에 각각의 자녀에 대한 개별 링크가 있는 것은 잘 동작하지 않습니다.대신 각 노드에서 트리의 최상위 자녀 및 그보다 작은 순서의 형제자매에 대한 링크를 사용하여 이 트리를 구현할 수 있습니다.이러한 형제 포인터는 각 노드의 자식 링크 리스트의 다음 포인터로 해석될 수 있지만 루트 링크 리스트의 순서와는 반대입니다.즉, 가장 큰 순서에서 가장 작은 순서로, 반대로 해석되지 않습니다.이 표현을 사용하면 같은 순서의 두 트리를 서로 연결하여 다음 순서의 트리를 일정한 ^[1]^[3]시간에 만들 수 있습니다.

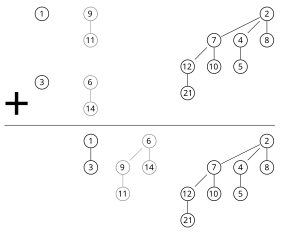
머지

같은 순서의 이항 트리를 병합하려면 먼저 루트 키를 비교합니다.7 > 3 이후 왼쪽(루트 노드 7 포함)의 검은 트리가 오른쪽(루트 노드 3)의 회색 트리에 서브트리로 부착됩니다.결과는 3차 트리입니다.

두 힙을 병합하는 작업은 대부분의 다른 작업에서 서브루틴으로 사용됩니다.이 절차 내의 기본 서브루틴은 같은 순서의 이항 트리의 쌍을 병합합니다.이것은, 2개의 트리의 루트에 있는 키(양쪽 트리에서 가장 작은 키)를 비교하는 것으로 실시할 수 있습니다.키가 큰 루트노드는 키가 작은 루트노드의 자노드로 만들어지며 순서는 ^[1]^[3]다음과 같이1개씩 증가합니다.

p.root.key <= q.root.key가 p.addSubTree(q)를 반환하는 경우 함수 mergeTree(p, q)가 q.addSubTree(p)를 반환합니다.

이것은 두 이항 힙의 병합을 보여줍니다.이 작업은 같은 순서의 이항 트리를 하나씩 병합하여 수행됩니다.결과적으로 병합된 트리의 순서가 두 힙 중 하나의 이항 트리와 같으면 두 개의 이항 트리가 다시 병합됩니다.

일반적으로 두 힙을 병합하기 위해 두 힙의 루트 목록은 병합 알고리즘과 유사한 방식으로 트리의 작은 순서에서 큰 순서로 동시에 통과됩니다.병합되는 두 힙 중 하나만 $순서$ j $\displaystyle$ j의 트리를 포함하는 경우 이 트리는 출력 힙으로 이동합니다.두 힙에 순서 $j$ 의 트리(\ $displaystyle$ j $)$ 가 포함되어 있는 경우 최소 힙 속성이 충족되도록 두 트리가 $j+1$ j + $j+1$ 의 $트리$ (\ $displaystyle$ j+1)로 $j+1$ 병합됩니다.나중에 이 트리를 2개의 입력 힙 중 하나로 j $j+1$ + $(\displaystyle$ j $+1)$ 의 $j+1$ 다른 트리와 병합해야 할 수 있습니다.알고리즘의 실행중에, 최대 3개의 트리(마지하는 2개의 힙으로부터 2개, 2개의 작은 ^[1]^[3]트리로 구성되는 트리)를 조사합니다.

heap.currentTree().empty() tree = mergeTree(p.end() 및 q.end()가 아닌 경우 mergeTree(p.currentTree), q.currentTree()의 heap.addTree(tree).

이항 힙의 각 이항 트리는 크기의 이진 표현에 있는 비트에 대응하므로, 두 힙의 병합과 두 힙의 크기의 이진 덧셈 사이에 오른쪽에서 왼쪽으로 유추됩니다.덧셈 중에 이항이 발생할 때마다 ^[1]^[3]이항 트리가 병합되는 동안 병합됩니다.

각 이항 트리의 Marge 중 트래버설은 루트만 포함되므로 로그 $\log _{2}n$ 의 $\log _{2}n$ 소요시간은 n $(\display\log_{2}n})$ 이므로 $\log _{2}n$ 실행시간은 O $O(\log n)$ n $)\displaystyle$ O $(\log$ n $O(\log n)$ ^[1]^[3]입니다.

삽입

새 요소를 힙에 삽입하려면 이 요소만 포함하는 새 힙을 만든 다음 원래 힙과 병합하면 됩니다.Marge에 의해 1개의 삽입에는 O $O(\log n)$ ( $O(\log n)$ n $O(\log n)$ ) { $displaystyle$ O ( \ $log$ n ) $O(\log n)$ }가 소요됩니다.단, Marge된 힙 중 하나에만 더 큰 순서의 트리가 있는 지점에 도달한 후 Marge를 단축하는 Marge 절차를 사용하여 이 작업을 가속화할 수 있습니다.이 속도 향상으로 $k$ 된 $k$ $k개의$ 삽입에 걸쳐 삽입의 총 시간은 O $(k$ $log$ n $)$ 입니다.다른 표현으로는 (시퀀스의 첫 $삽입$ 에 대한 로그 오버헤드 후) 연속된 삽입마다 O(\)의 $O(1)$ 상각 시간이 1 $(\)$ 입니다. $삽입당$ 표시 $스타일$ O(1 $)}($ ,^[1]^[3] 상수)

이항 힙의 변형인 스큐 이항 힙은 트리 크기가 2진수 ^[4]시스템이 아닌 스큐 2진수 시스템을 기반으로 하는 포레스트를 사용함으로써 최악의 경우 삽입 시간을 일정하게 달성합니다.

최소값 찾기

힙의 최소 요소를 찾으려면 이항 트리의 루트 중 최소 요소를 찾습니다.O $O(\log n)$ n $)\$ $displaystyle$ O $(\log$ n $)\$ displaystyle O(\log n)}개의 $O(\log n)$ $O(\log n)$ 트리 $O(\log n)$ 만 ^[1]있기 때문에 O $O(\log n)$ n)\ $displaystyle$ O $(\log$ n $)$ 시간 $O(\log n)$ 에 확인할 수 있습니다.

최소 요소를 포함하는 이항 트리에 대한 포인터를 사용하면 이 작업의 시간을 O ( $O(1)$ 1 ) $O(1)$ \ $display style$ O (1) $O(1)$ }(으)로 단축할 수 있습니다.최소값 찾기 이외의 작업을 수행할 때는 포인터를 업데이트해야 합니다.이것은 O $O(\log n)$ $O(\log n)$ n $)(\displaystyle$ O $(\log$ n $))$ 로 $O(\log n)$ 업데이트당 실행할 수 있으며 조작의 ^{[citation needed]}전체 점근적 실행 시간을 증가시키지 않습니다.

최소 삭제

힙에서 최소 요소를 삭제하려면 먼저 이 요소를 찾아 이항 트리의 루트에서 제거한 후 하위 하위 트리 목록(각 하위 트리 자체 이항 트리이며 순서가 구분됨)을 가져옵니다.가장 작은 순서에서 가장 큰 순서로 순서를 변경하여 이 하위 트리 목록을 별도의 이항 힙으로 변환합니다.그런 다음 이 힙을 원래 힙과 병합합니다.각 루트에는 $\log _{2}n$ 의 $\log _{2}n$ $로그가 있기$ 때문에 이 새로운 힙을 작성하려면 O $log$ n $O(\log n)$ $)(\$ $displaystyle$ O $(\log$ $O(\log n)$ n $O(\log n)$ 가 $O(\log n)$ 합니다.히프 머지에는 $O(\log n)$ ( $log$ n $O(\log n)$ 가 소요되므로 삭제 최소 $O(\log n)$ 에는 $O(\log n)$ O $($ n $)$ 가 소요됩니다.

함수 deleteMin(heap) min = heap.first()의 각 전류에 대해 current.root < min.root이면 min.subTrees() tmp.addTree(tree) 힙.removeTree(min)의 각 트리에 대해 merge(mp, tmp)

축소 키

요소의 키를 줄인 후 해당 요소의 키가 부모 키보다 작아져 최소 힙 속성을 위반할 수 있습니다.이 경우 최소 히프 속성이 위반되지 않을 때까지 요소를 부모 및 조부모와 교환합니다.각 이항 트리는 최대 $\log _{2}n$ $(\displaystyle \log$ _ ${2}n$ 의 높이를 가지므로 O $O(\log n)$ † $)\displaystyle$ O $(\log$ n $)}$ ^[1]시간이 $O(\log n)$ $O(\log n)$ .단, 이 조작에서는 트리의 표현에 각 노드에서 트리의 부모 노드로의 포인터가 포함되어 있어야 하므로 다른 ^[3]조작의 실장이 다소 복잡해집니다.

삭제

요소를 힙에서 삭제하려면 해당 키를 음의 무한대(또는 힙 내의 요소보다 낮은 값)로 줄인 다음 ^[1]힙 내의 최소값을 삭제합니다.

적용들

「」를 참조해 주세요.

이진 힙과 이항 힙 데이터 구조의 조합인 약한 힙

레퍼런스

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Chapter 19: Binomial Heaps". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 455–475. ISBN 0-262-03293-7.
^ Vuillemin, Jean (1 April 1978). "A data structure for manipulating priority queues". Communications of the ACM. 21 (4): 309–315. doi:10.1145/359460.359478.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Brown, Mark R. (1978). "Implementation and analysis of binomial queue algorithms". SIAM Journal on Computing. 7 (3): 298–319. doi:10.1137/0207026. MR 0483830.
^ Brodal, Gerth Stølting; Okasaki, Chris (November 1996), "Optimal purely functional priority queues", Journal of Functional Programming, 6 (6): 839–857, doi:10.1017/s095679680000201x

외부 링크

이항 힙의 2개의 C 실장(일반적인 실장 및 정수 키에 최적화된 실장)
이항 힙의 Haskell 구현
이항 힙의 일반적인 Lisp 구현

[clrs-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Chapter 19: Binomial Heaps". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 455–475. ISBN 0-262-03293-7.

[2] Vuillemin, Jean (1 April 1978). "A data structure for manipulating priority queues". Communications of the ACM. 21 (4): 309–315. doi:10.1145/359460.359478.

[brown-3] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Brown, Mark R. (1978). "Implementation and analysis of binomial queue algorithms". SIAM Journal on Computing. 7 (3): 298–319. doi:10.1137/0207026. MR 0483830.

[4] Brodal, Gerth Stølting; Okasaki, Chris (November 1996), "Optimal purely functional priority queues", Journal of Functional Programming, 6 (6): 839–857, doi:10.1017/s095679680000201x

[1]

[2]

[3]

[4]

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

이항 힙

네임스페이스

더

목차

이항 힙

이항 힙의 구조

실행

머지

삽입

최소값 찾기

최소 삭제

축소 키

삭제

적용들

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

이항 힙

이항 힙

이항 힙의 구조

실행

머지

삽입

최소값 찾기

최소 삭제

축소 키

삭제

적용들

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.