스플레이 트리

스플레이 트리
스플레이 트리
유형	트리
발명된	1985
발명자	다니엘 도미닉 슬레토르와 로버트 엔드레 타잔
빅 O 표기법에서의 복잡도
공간
공간의 복잡성
공간
시간의 복잡성
기능.
서치
삽입
삭제

스플레이 트리는 최근에 액세스한 요소가 빠르게 다시 액세스할 수 있는 추가 속성이 있는 이진 검색 트리입니다.자가 밸런싱 바이너리 검색 트리와 마찬가지로 스플레이 트리는 O(log n) 상각 시간 내에 삽입, 룩업 및 제거와 같은 기본 작업을 수행합니다.불균일한 랜덤 분포에서 도출된 랜덤 액세스 패턴의 경우, 상각된 시간은 액세스 패턴의 엔트로피에 비례하여 로그보다 빠를 수 있습니다.또한 많은 비랜덤 연산 패턴의 경우 패턴에 대한 사전 지식이 없어도 스플레이 트리가 로그 시간보다 더 오래 걸릴 수 있습니다.증명되지 않은 동적 최적성 추측에 따르면 모든 접근 패턴에서의 퍼포먼스는 다른 어떤 자체 조정 바이너리 검색 트리에 의해 달성될 수 있는 최고의 퍼포먼스의 일정한 요소 내에 있습니다.그 패턴에 맞도록 선택된 바이너리 검색 트리라도 마찬가지입니다.스플레이 트리는 1985년 ^[1]다니엘 슬레이터와 로버트 타잔에 의해 발명되었다.

이진 검색 트리의 모든 일반 연산은 분할이라는 하나의 기본 연산과 결합됩니다.특정 요소에 대해 트리를 분할하면 트리가 트리 루트에 배치되도록 정렬됩니다.기본 검색 조작으로 이를 수행하는 한 가지 방법은 먼저 해당 요소에 대해 표준 이진 트리 검색을 수행한 다음 특정 방식으로 트리 회전을 사용하여 요소를 맨 위로 가져오는 것입니다.또는 하향식 알고리즘은 검색과 트리 재구성을 단일 단계로 결합할 수 있습니다.

이점

스플레이 트리의 뛰어난 성능은 자주 액세스하는 노드가 보다 빠르게 액세스할 수 있는 루트에 가까워진다는 자체 최적화 여부에 달려 있습니다.최악의 경우 높이는 O(n)이며, 평균은 O(log n)입니다.루트 근처에 자주 사용되는 노드가 있는 것은 많은 실용적인 응용 프로그램(참조 위치 참조)의 이점이며 캐시 및 가비지 수집 알고리즘을 구현하는 데 특히 유용합니다.

장점은 다음과 같습니다.

동등한 퍼포먼스:평균 케이스 퍼포먼스는 다른 ^[3]트리와 마찬가지로 효율적입니다.
메모리 공간 절약: 스플레이 트리는 부기 데이터를 저장할 필요가 없습니다.

단점들

스플레이 트리의 가장 큰 단점은 스플레이 트리의 높이가 ^[2]^{: 1}선형일 수 있다는 것입니다.예를 들어 n개의 요소에 모두 비감소 순서로 접근한 후가 이에 해당합니다.트리의 높이는 최악의 액세스 시간에 대응하므로, 이것은 단일 조작의 실제 비용이 높을 수 있음을 의미합니다.그러나 이 최악의 경우 상각된 액세스 비용은 로그 O(log n)입니다.또, 랜덤화된 ^[4]변종을 이용하는 것으로, 기대 액세스 코스트를 O(log n)까지 저감 할 수 있다.

스플레이 트리의 표현은 '읽기 전용' 방식으로 액세스되는 경우에도(즉, 찾기 작업을 통해) 변경될 수 있습니다.이로 인해 멀티 스레드 환경에서 이러한 스플레이 트리의 사용이 복잡해집니다.특히 여러 스레드가 동시에 찾기 작업을 수행할 수 있는 경우 추가 관리가 필요합니다.이 때문에 priority 큐를 구현하기 위해 제한된 방법으로 사용할 수 있지만 순수 기능적 프로그래밍에서는 일반적으로 사용하기에는 적합하지 않습니다.

마지막으로, 액세스 패턴이 랜덤인 경우, 추가 분할 오버헤드는 덜 역동적인 대체 요소에 비해 비용에 중요한 고정 요소를 추가합니다.

운용

스플라이잉

노드 x에 액세스하면 x에 대해 스플레이 연산을 실행하여 노드 x를 루트로 이동합니다.스플레이 작업을 수행하기 위해 일련의 스플레이 단계를 수행합니다. 스플레이 단계는 각각 x를 루트에 가깝게 움직입니다.액세스 후 대상 노드에서 스플레이 연산을 실행함으로써 최근 액세스된 노드가 루트 근처에 유지되고 트리는 대략적인 균형을 유지하므로 원하는 상각된 시간 범위를 달성할 수 있습니다.

각 단계는 다음 세 가지 요인에 따라 달라집니다.

x가 부모 노드 p의 왼쪽 자식인지 오른쪽 자식인지에 관계없이
p가 루트인지 아닌지를 확인합니다.
p가 부모 g(x의 조부모)의 왼쪽 또는 오른쪽 자식인지 여부.

스플레이 조작 후에 gg(x의 증조)를 x를 가리키도록 설정하는 것이 중요합니다.gg가 null인 경우 x가 루트가 되므로 업데이트해야 합니다.

스플레이 단계에는 세 가지 유형이 있으며, 각각 왼쪽과 오른쪽의 두 가지 대칭 변형이 있습니다.간결하게 하기 위해 각 유형별로 이 두 가지 중 하나만 표시됩니다.(다음 그림에서 원은 관심 노드를 나타내고 삼각형은 임의의 크기의 하위 트리를 나타냅니다.)세 가지 유형의 스플레이 단계는 다음과 같습니다.

Zig 스텝: 이 스텝은 p가 루트일 때 실행됩니다.트리는 x와 p 사이의 가장자리에서 회전합니다. Zig 스텝은 패리티 문제를 처리하기 위해 존재하며, 스플레이 동작의 마지막 스텝으로만 수행되며, 동작 시작 시 x의 깊이가 홀수인 경우에만 수행됩니다.

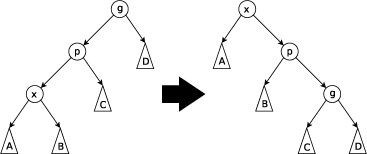
Zig-zig 스텝: 이 스텝은 p가 루트가 아니고 x와 p가 둘 다 오른쪽 아이이거나 둘 다 왼쪽 아이일 때 수행됩니다.아래 그림은 x와 p가 둘 다 왼쪽 자녀인 경우입니다.트리는 부모 g와 함께 p를 결합하는 모서리에서 회전한 다음 x와 p를 결합하는 모서리에서 회전합니다.지그지그 스텝은 스플레이 트리를^[5] 도입하기 전에 앨런과 먼로가 도입한 로테이션 투 루트 방식과 구별하는 유일한 방법이라는 점에 주의해 주십시오.

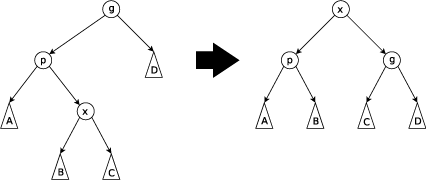
지그재그 스텝: 이 스텝은 p가 루트가 아니고 x가 오른쪽 아이이고 p가 왼쪽 아이이거나 그 반대일 때 실행됩니다(x는 왼쪽, p는 오른쪽).트리는 p와 x 사이의 가장자리에서 회전한 다음 x와 g 사이의 결과 가장자리에서 회전합니다.

합류하다

S의 모든 요소가 T의 요소보다 작도록 2개의 트리 S와 T를 지정하면 다음 단계를 사용하여 이들을 단일 트리에 결합할 수 있습니다.

S에서 가장 큰 아이템을 분할합니다.이제 이 항목은 S의 루트에 있고 오른쪽의 Null 하위 항목이 있습니다.
새 루트의 오른쪽 자식을 T로 설정합니다.

분열되다

트리와 요소 x를 지정하면 두 개의 새 트리를 반환합니다. 하나는 x보다 작거나 같은 모든 요소를 포함하고 다른 하나는 x보다 큰 모든 요소를 포함합니다.이것은, 다음의 방법으로 실시할 수 있습니다.

스플레이 x. 이제 루트에 있으므로 왼쪽 트리는 x보다 작은 모든 요소를 포함하고 오른쪽 트리는 x보다 큰 모든 요소를 포함합니다.
트리의 나머지 부분으로부터 오른쪽 서브트리를 분할합니다.

삽입

값 x를 스플레이 트리에 삽입하려면:

일반 바이너리 검색 트리와 마찬가지로 x를 삽입합니다.
항목이 삽입되면 스플레이가 수행됩니다.
그 결과 새로 삽입된 노드 x가 트리의 루트가 된다.

대체 방법:

분할 연산을 사용하여 x 값으로 트리를 2개의 서브 트리(S 및 T)로 분할합니다.
x가 루트, S가 왼쪽 서브트리, T가 오른쪽 서브트리로 구성된 새 트리를 만듭니다.

삭제

노드 x를 삭제하려면 바이너리 검색 트리와 같은 방법을 사용합니다.

x에 2명의 자녀가 있는 경우:
- 이 값을 왼쪽 서브트리의 오른쪽 끝 노드(순서대로 이전 노드) 또는 오른쪽 서브트리의 왼쪽 끝 노드(순서대로 후속 노드) 중 하나로 바꿉니다.
- 대신 해당 노드를 제거하십시오.

이렇게 하면 삭제가 0 또는 1의 자녀가 있는 노드를 삭제하는 문제로 줄어듭니다.바이너리 검색 트리와 달리 삭제 후 분할 트리에서 제거된 노드의 부모를 트리 맨 위에 분할합니다.

대체 방법:

삭제할 노드가 먼저 분할됩니다. 즉, 트리의 루트로 가져온 다음 삭제됩니다.두 개의 하위 트리가 있는 트리를 남깁니다.
그런 다음 "join" 연산을 사용하여 두 개의 하위 트리가 결합됩니다.

구현 및 변형

위에서 설명한 바와 같이 스플레이잉은 노드의 액세스 경로 상에서 두 번째 상향식 패스 중에 수행됩니다.첫 번째 패스 중에 액세스 패스를 기록할 수 있지만 두 번째 패스 중에 사용할 수 있도록 하려면 액세스 조작 중에 여분의 공간이 필요합니다.또 하나의 대안은 부모 포인터를 모든 노드에 유지하는 것입니다.이것에 의해, 액세스 조작중에 여분의 공간이 필요 없게 됩니다만,^[1] 이러한 포인터를 갱신할 필요가 있기 때문에, 전체적인 시간의 효율이 저하될 수 있습니다.

사용할 수 있는 또 다른 방법은 두 번째 패스를 하지 않고 접근경로를 내려가는 길에 트리를 재구성할 수 있다는 인수에 기초하고 있습니다.이 하향식 분할 루틴에서는 왼쪽 트리, 오른쪽 트리 및 중간 트리라는 세 세트의 노드를 사용합니다.처음 두 개의 항목은 각각 현재 항목보다 작거나 큰 것으로 알려진 원래 트리의 모든 항목을 포함합니다.중간 트리는 현재 노드에 루트된 하위 트리로 구성됩니다.이들 3세트는 스플레이 동작을 체크하면서 접근경로를 따라 갱신됩니다.또 다른 방법인 세미플레이는 지그지그 케이스를 수정하여 모든 작업에서 수행되는 ^[1]^[6]재구성의 양을 줄입니다.

아래는 C++의 스플레이 트리의 구현으로, 트리의 각 노드를 나타내는 포인터를 사용합니다.이 구현은 상향식 분할 버전을 기반으로 하며 분할 트리에서 두 번째 삭제 방법을 사용합니다.또한 위의 정의와 달리 이 C++ 버전은 트리를 찾을 때 트리를 분할하지 않습니다.삽입 및 삭제 시에만 분할되므로 찾기 작업이 선형적으로 복잡해집니다.

#실패하다 <기능>  #ifndef SPLAY_TREE #SLAY_TREE의 정의  템플릿< >타이프네임 T, 타이프네임 컴포넌트 = 표준::더 적은< >T>> 학급 스플라이 트리 { 사적인:   컴포넌트 컴포넌트;   서명되어 있지 않다 긴 p_size;      구조 노드 {     노드 *왼쪽, *맞다;     노드 *부모;     T 열쇠;     노드(컨스턴트 T& 초기화 = T()) : 왼쪽(특수), 맞다(특수), 부모(특수), 열쇠(초기화) { }     ~노드() {      }   } *뿌리;      무효 왼쪽_바깥쪽(노드 *x) {     노드 *y = x->맞다;     한다면 (y) {       x->맞다 = y->왼쪽;       한다면 (y->왼쪽) y->왼쪽->부모 = x;       y->부모 = x->부모;     }          한다면 (!x->부모) 뿌리 = y;     또 다른 한다면 (x == x->부모->왼쪽) x->부모->왼쪽 = y;     또 다른 x->부모->맞다 = y;     한다면 (y) y->왼쪽 = x;     x->부모 = y;   }      무효 right_filename(오른쪽)(노드 *x) {     노드 *y = x->왼쪽;     한다면 (y) {       x->왼쪽 = y->맞다;       한다면 (y->맞다) y->맞다->부모 = x;       y->부모 = x->부모;     }     한다면 (!x->부모) 뿌리 = y;     또 다른 한다면 (x == x->부모->왼쪽) x->부모->왼쪽 = y;     또 다른 x->부모->맞다 = y;     한다면 (y) y->맞다 = x;     x->부모 = y;   }      무효 스플래시(노드 *x) {     하는 동안에 (x->부모) {       한다면 (!x->부모->부모) {         한다면 (x->부모->왼쪽 == x) right_filename(오른쪽)(x->부모);         또 다른 왼쪽_바깥쪽(x->부모);       } 또 다른 한다면 (x->부모->왼쪽 == x & & x->부모->부모->왼쪽 == x->부모) {         right_filename(오른쪽)(x->부모->부모);         right_filename(오른쪽)(x->부모);       } 또 다른 한다면 (x->부모->맞다 == x & & x->부모->부모->맞다 == x->부모) {         왼쪽_바깥쪽(x->부모->부모);         왼쪽_바깥쪽(x->부모);       } 또 다른 한다면 (x->부모->왼쪽 == x & & x->부모->부모->맞다 == x->부모) {         right_filename(오른쪽)(x->부모);         왼쪽_바깥쪽(x->부모);       } 또 다른 {         왼쪽_바깥쪽(x->부모);         right_filename(오른쪽)(x->부모);       }     }   }      무효 교체하다(노드 *u, 노드 *v) {     한다면 (!u->부모) 뿌리 = v;     또 다른 한다면 (u == u->부모->왼쪽) u->부모->왼쪽 = v;     또 다른 u->부모->맞다 = v;     한다면 (v) v->부모 = u->부모;   }      노드* 서브트리_오브젝트(노드 *u) {     하는 동안에 (u->왼쪽) u = u->왼쪽;     돌아가다 u;   }      노드* 서브트리_최대(노드 *u) {     하는 동안에 (u->맞다) u = u->맞다;     돌아가다 u;   } 일반의:   스플라이 트리() : 뿌리(특수), p_size(0) { }      무효 삽입하다(컨스턴트 T &열쇠) {     노드 *z = 뿌리;     노드 *p = 특수;          하는 동안에 (z) {       p = z;       한다면 (컴포넌트(z->열쇠, 열쇠)) z = z->맞다;       또 다른 z = z->왼쪽;     }          z = 신규 노드(열쇠);     z->부모 = p;          한다면 (!p) 뿌리 = z;     또 다른 한다면 (컴포넌트(p->열쇠, z->열쇠)) p->맞다 = z;     또 다른 p->왼쪽 = z;          스플래시(z);     p_size++;   }      노드* 발견하다(컨스턴트 T &열쇠) {     노드 *z = 뿌리;     하는 동안에 (z) {       한다면 (컴포넌트(z->열쇠, 열쇠)) z = z->맞다;       또 다른 한다면 (컴포넌트(열쇠, z->열쇠)) z = z->왼쪽;       또 다른 돌아가다 z;     }     돌아가다 특수;   }            무효 지우다(컨스턴트 T &열쇠) {     노드 *z = 발견하다(열쇠);     한다면 (!z) 돌아가다;          스플래시(z);          한다면 (!z->왼쪽) 교체하다(z, z->맞다);     또 다른 한다면 (!z->맞다) 교체하다(z, z->왼쪽);     또 다른 {       노드 *y = 서브트리_오브젝트(z->맞다);       한다면 (y->부모 != z) {         교체하다(y, y->맞다);         y->맞다 = z->맞다;         y->맞다->부모 = y;       }       교체하다(z, y);       y->왼쪽 = z->왼쪽;       y->왼쪽->부모 = y;     }          삭제하다 z;     p_size--;   }  /* //대체 구현 무효 소거(계속 T&키) { 노드 *z = find(키); (!z)가 반환되는 경우;          스플라이(z);          노드 *s = z-> 왼쪽; 노드 *t = z->오른쪽; z를 삭제합니다;          노드 *sMax = NULL; (s)의 경우 s-> parent = NULL; sMax = subtree_maximum(s); 스플라이(sMax); 루트 = sMax; } (t)의 경우 (s)의 경우 sMax->오른쪽 = t; 또 다른 루트 = t; t->부모 = sMax; }          p_size--; } */      컨스턴트 T& 최소의() { 돌아가다 서브트리_오브젝트(뿌리)->열쇠; }   컨스턴트 T& 최대치() { 돌아가다 서브트리_최대(뿌리)->열쇠; }      부울 빈() 컨스턴트 { 돌아가다 뿌리 == 특수; }   서명되어 있지 않다 긴 크기() 컨스턴트 { 돌아가다 p_size; } };  #엔디프// 스플레이_트리

분석.

이 전위법을 사용하여 정적 스플레이 트리의 간단한 상각분석을 실시할 수 있다.정의:

size(r) = 노드 r(r 포함)에 루트된 서브트리 내 노드의 수.
rank(r) = log₂(size(r)).
δ = 트리 내 모든 노드의 순위 합계.

δ는 균형이 맞지 않는 나무는 높고 균형이 잘 잡힌 나무는 낮은 경향이 있습니다.

전위법을 적용하기 위해 먼저 스플레이 연산에 의한 전위 변화인 δ을 계산한다.케이스별로 체크합니다.작업 후 순위'로 순위 함수를 나타냅니다.x, p 및 g는 회전 동작의 영향을 받는 노드입니다(위 그림 참조).

지그 스텝

ΔΦ	= 랭크'(p) - 랭크(p) + 랭크'(x) - 랭크(x)	[P와 X만 순위가 바뀌기 때문에]
	= 랭크'(p) - 랭크(x)	[랭크(x)=랭크(p) 이후]
	§ 랭크'(x) - 랭크(x)	[랭크(p) 이후 <랭크(x)]

지그재그 스텝

ΔΦ	= 랭크'(g) - 랭크(g) + 랭크(p) - 랭크(p) + 랭크'(x) - 랭크(x)
	= 랭크'(g) + 랭크'(p) - 랭크(p) - 랭크(x)	[랭크(x)=랭크(g) 이후]
	§ 랭크'(g) + 랭크'(x) - 2랭크(x)	[랭크(x) 이후 <랭크(p) 및 랭크(x)>랭크(p)]
	§ 3(랭크'(x)-랭크(x)-2	[로그 함수의 오목함 때문에]

지그재그 스텝

ΔΦ	= 랭크'(g) - 랭크(g) + 랭크(p) - 랭크(p) + 랭크'(x) - 랭크(x)
	§ 랭크'(g) + 랭크'(p) - 2랭크(x)	[rank'(x)=rank(g) 및 rank(x) <rank(p)>
	§ 3(랭크'(x)-랭크(x)-2	[로그 함수의 오목함 때문에]

모든 작업에 대한 상각 비용은 φ에 실제 비용을 더한 금액입니다.지그재그 또는 지그재그 동작의 실제 비용은 2회전이 필요하기 때문에 2회입니다.이 때문에,

상각비의	= 비용 + δδ
	§ 3(랭크)(x)-랭크(x)

전체 스플레이 연산을 합산하면, 이 망원경은 O(log n)인 3(rank(root)-rank(x)까지 확장됩니다.Zig 연산은 상각비용 1을 더하지만, 이러한 연산은 기껏해야 1개입니다.

이제 일련의 m 연산에 대해 상각된 총 시간은 다음과 같습니다.

{displaystyle T_{\mathrm {sysized}}(m)=O(m\log n)}

상각된 시간에서 실제 시간으로 이동하기 위해서는 모든 작업이 완료된 후(φ_i) 최종 상태에 모든 작업이 완료되기 전의 초기 상태(φ)에서 잠재력 감소를 더해야 합니다(φ_f).

\displaystyle \Phi _{f}=\sum _{x}{\mathrm {rank}_{i}(x)-\mathrm {rank}_{f}(x)=O(n\log n)}

여기서 마지막 부등식은 모든 노드 x에 대해 최소 순위는 0이고 최대 순위는 log(n)이다.

이제 드디어 실제 시간을 제한할 수 있습니다.

({displaystyle T_{\mathrm {display}}}(m)=O(m\log n+n\log n)}

가중 분석

위의 분석은 다음과 같이 일반화할 수 있다.

무게 w(r)를 각 노드에 할당합니다.
size(r) = 노드 r(r 포함)에 루트된 하위 트리의 노드 가중치 합계를 정의합니다.
위와 같이 랭크(r)와 δ를 정확히 정의하십시오.

동일한 분석이 적용되며 분할작업의 상각원가는 다시 다음과 같습니다.

\displaystyle \mathrm {rank}(root)-\mathrm {rank}(x)=O(\log {W}-\log {w(x)})=O\left(\log {W}{w(x)}}\right)}

여기서 W는 모든 무게의 합계입니다.

초기 전위부터 최종 전위까지의 감소는 다음과 같이 제한된다.

\displaystyle \Phi _{i}-\Phi _{f}\leq \sum _{x\in tree}{\log \frac {W}{w(x)}}}}

단일 노드의 최대 사이즈는 W이고 최소 사이즈는 w(x)이기 때문입니다.

따라서 실제 시간은 다음과 같이 제한됩니다.

O\left(\sum _{x\in sequence}{\log {frac {W}{w(x)}}+\sum _{x\in tree}{\log {frac {W}{w(x)}}}\right

퍼포먼스 정리

n개의 요소를 포함하는 스플레이 트리에서 m개의 액세스 시퀀스 S를 수행하기 위한 최악의 경우 런타임에 관한 몇 가지 이론과 추측이 있다.

Balance Orginary : 시퀀스S $O\left[m\log n+n\log n\right]$ 비용은 O [ $O\left[m\log n+n\log n\right]$ log $O\left[m\log n+n\log n\right]$ + n $O\left[m\log n+n\log n\right]$ log $O\left[m\log n+n\log n\right]$ \ $displaystyle$ O \ $left$ [ $m$ \ $log$ n + $n$ \ $log$ n \ $right$ 입니다.

증명

모든 노드 x에 대해 w ( $w(x)=1$ ) $=$ 1 { $displaystyle$ w $(x$ 1 $}$ 과 $w(x)=1$ $같이$ 일정한 가중치를 측정합니다. $W=n$ 으로 W $W=n$ \ $displaystyle$ W $=n$ 입니다 $W=n$

이 정리는 스플레이 트리가 최소 n개의 ^[1]액세스 시퀀스에서 정적 균형 이진 검색 트리만큼 잘 수행된다는 것을 의미합니다.

Static Optimality Correm: $q_{x}$ x { $displaystyle q$ _ { $x$ } $q_{x}$ 、 S s x x isx in x isx 。모든 요소에 1회 이상 액세스할 경우 S를 실행하는 비용은 $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ O [ $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ + $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ + $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ t $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ r $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ x $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ mm $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ x $O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]$ ]{ $style$ O\ $left$ [ $m+\sum$ _ ${x\in$ tree $}q_{x}\log {frac {m}{q_x}}\$ right $}$ 입니다.

증명

$w(x)=q_{x}$ ( $w(x)=q_{x}$ ) $w(x)=q_{x}$ $w(x)=q_{x}$ x {\ $displaystyle$ w $(x$ )= $q_{x$ 다음으로 $W=m$ $W=m$ $W=m$ ${\displaystyle$ W $=m$

이 정리는 스플레이 트리가 최소 n개의 ^[7]액세스 시퀀스에 대해 최적의 정적 이진 검색 트리만큼 잘 수행된다는 것을 의미합니다.그들은 더 빈번한 항목에 ^[1]더 적은 시간을 소비한다.같은 결과를 나타내는 또 다른 방법은 항목이 n개 항목에 대한 불균일한 확률 분포로부터 독립적으로 랜덤하게 도출되는 입력 시퀀스에서 각 접근의 상각 예상(평균 케이스) 비용이 ^[8]분포의 엔트로피에 비례하는 것이다.

정적 핑거 정리: 항목에 오름차순으로 번호가 매겨진다고 가정합니다.f를 임의의 고정 요소('핑거')로 합니다.다음으로 S를 실행하는 $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ 은 $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ + n log $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ + $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ n $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ ( x $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ - $O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]$ + 1 $)\$ $displaystyle$ O $\ left$ [ m + $n$ \ $log$ n + \ $sum$ _ { x \ in $sequence$ }\ log ( x $- f$ + $1$ )\ $right$ 입니다.

증명

$w(x)=1/(|x-f|+1)^{2}$ ( $w(x)=1/(|x-f|+1)^{2}$ x ) $w(x)=1/(|x-f|+1)^{2}$ / ( $w(x)=1/(|x-f|+1)^{2}$ - $w(x)=1/(|x-f|+1)^{2}$ + $w(x)=1/(|x-f|+1)^{2}$ ) 2 $w(x)=1/(|x-f|+1)^{2}$ {{ $displaystyle$ w ( x ) = $1$ / ( x - f + $1$ )^{ $2$ 그 $W=O(1)$ W $W=O(1)$ ( $W=O(1)$ ) { $displaystyle$ W $= O$ (1) $W=O(1)$ } $W=O(1)$ 。임의의 항목의 무게가 최소 $1/n^{2}$ / $({$ 1/ $n^{2$ ^[1]이므로 순전위하중은 O(n log n)입니다.

동적 핑거 정리 - 요소 y에 액세스하는 각 단계의 '핑거'가 이전 단계 x에서 액세스한 요소라고 가정합니다.S를 실행하는 $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ 은 $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ [ $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ + n + $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ , $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ e $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ e $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ log $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ - $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ + $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ ]{ $display O \ left$ [ m + n + \ $sum _$ { x , y \ in sequence }^{ $m }$ \ $log$ ( $y$ - x + 1) \ right $O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]$ ^[9]^[10] 입니다.

작업 세트 정리: 시퀀스 중에 언제든지 t $t(x)$ ( $t(x)$ ) { $displaystyle$ t $(x)}$ 을 $t(x)$ (를) 이전 시간 요소 x에 액세스하기 전에 액세스한 개별 요소의 수로 $t(x)$ . $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ 를 실행하는 $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ 은 $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ O [ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ log $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ e log $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ ( $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ ( $O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]$ ) + $]{$ $displaystyle$ O \ $left$ [ m + $n$ \ $log$ n + \ $sum$ _ ${ x$ \ $in$ sequence }\ $log$ ( $x$ + 1 $)$ \ $right$ } 입니다.

증명

$w(x)=1/(t(x)+1)^{2}$ ( $w(x)=1/(t(x)+1)^{2}$ ) $w(x)=1/(t(x)+1)^{2}$ / ( $w(x)=1/(t(x)+1)^{2}$ ( $w(x)=1/(t(x)+1)^{2}$ ) + $w(x)=1/(t(x)+1)^{2}$ ) $w(x)=1/(t(x)+1)^{2}$ {{ $displaystyle$ w $(x$ ) = $1/(t(x)+1$ )^2 $w(x)=1/(t(x)+1)^{2}$ 로 합니다.여기서 무게는 시퀀스 중에 변화합니다.그러나 무게의 순서는 $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ 1, $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ 1 $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ , $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ 9 $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ 1 $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ ,, $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ $({$ 1, {\ $tfrac {$ 1}{4 $}},$ {\ $tfrac$ {1 $}{9}}),$ \ $cdots,$ {\ $tfrac {1}{n^{$ 2 $1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}$ 의 순열입니다. 따라서 W $= 1$ 1 $)$ $W=O(1)$ 과 같습니다.순잠재적 폐기는 O(n log n)입니다.

이 정리는 키에 의존하지 않는 최적성을 ^[1]갖는 스플레이 트리와 동등합니다.

스캔 정리: 시퀀셜액세스 정리 또는 큐 정리라고도 불립니다.스플레이 ^[11]트리의 초기 구조에 관계없이 대칭 순서로 스플레이 트리의 n개 요소에 액세스하려면 O(n) 시간이 걸립니다. $지금$ 까지 입증된 가장 엄격한 상한선은 $5n$ 입니다 $4.5n$ ^[12]

동적 최적성 추측

컴퓨터 과학에서 해결되지 않은 문제:

스플레이 트리는 다른 바이너리 검색 트리 알고리즘과 같은 성능을 발휘합니까?

(컴퓨터 사이언스의 미해결 문제 증가)

스플레이 트리에 대한 입증된 성능 보증 외에도, 원본 Sleator 및 Tarjan 논문으로부터 많은 관심을 받고 있는 입증되지 않은 추측이 있습니다.이 추측은 동적 최적성 추측으로 알려져 있으며 기본적으로 스플레이 트리가 일정한 요소까지 다른 이진 검색 트리 알고리즘과 마찬가지로 수행한다고 주장한다.

동적 최적성 추측:^[1]

(\displaystyle

A

)

는

A

요소

x

(\displaystyle

x

)

에

x

x

대한 경로를 d

d(x)+1

+

d(x)+1

(\

displaystyle

d

(x)+1

의 비용으로 통과하여 액세스 간에 트리를 회전시키는 바이너리 검색 트리 알고리즘입니다.A

)

{

style

A

(S

)} {

displaystyle

A

}

이

A(S)

A

(

가

) 액세스 시퀀스

S(\

displaystyle

S

)

를 실행하기

위한

비용을 A

(S

) {displaystyle A(S

)

{\displaystyle S}로

S

A(S)

.같은 접근을 실행하는 스플레이 트리의 비용은 O

O[n+A(S)]

[

O[n+A(S)]

+

O[n+A(S)]

(

O[n+A(S)]

S )

]{

display

O [

n

+

A

( S )

O[n+A(S)]

입니다.

검증되지 않은 상태로 남아 있는 동적 최적성 추측에는 다음과 같은 몇 가지 결과가 있습니다.

통과 추측:^[1]

({

T_

{1})

과

T_{1}

({

를

T_{2}

동일한 요소를 포함하는 2개의 스플라이 트리로

T_{1}

.

(\displaystyle

S

)

는

S

(\

의

T_{2}

요소를 사전 순서(즉 깊이 우선 검색 순서)로 방문한 시퀀스입니다.

({

에서

T_{1}

액세스

({displaystyle

S})를

S

실행하는 총 비용은

O(n)

(n

O(n)

{displaystyle

O

(n

입니다.

추측:^[11]^[13]^[14]S

{\displaystyle

S

}

를

S

m

{\

displaystyle

m

}

의

m

더블 엔드 큐 조작(푸시, 팝, 주입, 이젝트)으로

합니다

.스플레이 트리에서 S

(\display style

S

)

를

S

실행하는 데

O(m+n)

비용은 O

O(m+n)

+

)

{\

display

style

O(m+

n

O(m+n)

입니다.

스플릿 추측:^[6]

S

(\

displaystyle

S

)

는

S

스플레이 트리 요소의 배열입니다.

(\displaystyle

S

)

순서로

S

요소를 삭제하는 비용은 O

)

{

displaystyle

O

(n

입니다.

변종

재구성 작업 횟수를 줄이기 위해 요소를 ^[1]^[2]루트를 향해 반만 분할하는 반분할로 대체할 수 있다.

재구성을 줄이는 또 다른 방법은 풀스플레이잉을 실행하는 것입니다.단, 액세스패스가 임계값보다 길 때 또는 첫 번째 m 액세스 ^[1]동작에서만 실시합니다.

「」를 참조해 주세요.

메모들

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ Sleator & Tarjan 1985.
^ ^a ^b ^c Brinkmann, Degraer & De Loof 2009.
^ Goodrich, Tamassia & Goldwasser 2014.
^ Albers & Karpinski 2002.
^ 앨런 & 먼로 1978.
^ ^a ^b 루카스 1991년
^ Knuth 1997, 478페이지
^ Greenberg 외 연구진(1995년)
^ 콜 등 2000년.
^ 콜 2000
^ ^a ^b 타잔 1985년
^ 2004년 엘마스리
^ Pettie 2008.
^ 순다르 1992년

레퍼런스

Albers, Susanne; Karpinski, Marek (28 February 2002). "Randomized Splay Trees: Theoretical and Experimental Results" (PDF). Information Processing Letters. 81 (4): 213–221. doi:10.1016/s0020-0190(01)00230-7.
Allen, Brian; Munro, Ian (October 1978). "Self-organizing binary search trees". Journal of the ACM. 25 (4): 526–535. doi:10.1145/322092.322094. S2CID 15967344.
Brinkmann, Gunnar; Degraer, Jan; De Loof, Karel (January 2009). "Rehabilitation of an unloved child: semi-splaying" (PDF). Software: Practice and Experience. 39 (1): 33–45. CiteSeerX 10.1.1.84.790. doi:10.1002/spe.v39:1. hdl:11382/102133. The results show that semi-splaying, which was introduced in the same paper as splaying, performs better than splaying under almost all possible conditions. This makes semi-splaying a good alternative for all applications where normally splaying would be applied. The reason why splaying became so prominent while semi-splaying is relatively unknown and much less studied is hard to understand.
Cole, Richard; Mishra, Bud; Schmidt, Jeanette; Siegel, Alan (January 2000). "On the Dynamic Finger Conjecture for Splay Trees. Part I: Splay Sorting log n-Block Sequences". SIAM Journal on Computing. 30 (1): 1–43. CiteSeerX 10.1.1.36.4558. doi:10.1137/s0097539797326988.
Cole, Richard (January 2000). "On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof". SIAM Journal on Computing. 30 (1): 44–85. CiteSeerX 10.1.1.36.2713. doi:10.1137/S009753979732699X.
Elmasry, Amr (April 2004). "On the sequential access theorem and Deque conjecture for splay trees". Theoretical Computer Science. 314 (3): 459–466. doi:10.1016/j.tcs.2004.01.019.
Goodrich, Michael; Tamassia, Roberto; Goldwasser, Michael (2014). Data Structures and Algorithms in Java (6 ed.). Wiley. p. 506. ISBN 978-1-118-77133-4.
Grinberg, Dennis; Rajagopalan, Sivaramakrishnan; Venkatesan, Ramarathnam; Wei, Victor K. (1995). "Splay trees for data compression". In Clarkson, Kenneth L. (ed.). Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, 22–24 January 1995. San Francisco, California, USA. ACM/SIAM. pp. 522–530. Average depth of access in a splay tree is proportional to the entropy.
Knuth, Donald (1997). The Art of Computer Programming. Vol. 3: Sorting and Searching (3rd ed.). Addison-Wesley. p. 478. ISBN 0-201-89685-0. The time needed to access data in a splay tree is known to be at most a small constant multiple of the access time of a statically optimum tree, when amortized over any series of operations.
Lucas, Joan M. (1991). "On the Competitiveness of Splay Trees: Relations to the Union-Find Problem". On-line Algorithms: Proceedings of a DIMACS Workshop, February 11–13, 1991. Series in Discrete Mathematics and Theoretical Computer Science. Vol. 7. Center for Discrete Mathematics and Theoretical Computer Science. pp. 95–124. ISBN 0-8218-7111-0.
Pettie, Seth (2008). Splay Trees, Davenport-Schinzel Sequences, and the Deque Conjecture (PDF). Proc. 19th ACM-SIAM Symposium on Discrete Algorithms. Vol. 0707. pp. 1115–1124. arXiv:0707.2160. Bibcode:2007arXiv0707.2160P.
Sleator, Daniel D.; Tarjan, Robert E. (1985). "Self-Adjusting Binary Search Trees" (PDF). Journal of the ACM. 32 (3): 652–686. doi:10.1145/3828.3835. S2CID 1165848.
Sundar, Rajamani (1992). "On the Deque conjecture for the splay algorithm". Combinatorica. 12 (1): 95–124. doi:10.1007/BF01191208. S2CID 27422556.
Tarjan, Robert E. (1985). "Sequential access in splay trees takes linear time". Combinatorica. 5 (4): 367–378. doi:10.1007/BF02579253. S2CID 34757821.

외부 링크

[SleatorTarjan-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ Sleator & Tarjan 1985.

[BrinkmannDegraerDeLoof-2] Brinkmann, Degraer & De Loof 2009.

[3] Goodrich, Tamassia & Goldwasser 2014.

[4] Albers & Karpinski 2002.

[AllenMunro-5] 앨런 & 먼로 1978.

[Lucas-6] 루카스 1991년

[7] Knuth 1997, 478페이지

[FOOTNOTEGrinbergRajagopalanVenkatesanWei1995-8] Greenberg 외 연구진(1995년)

[ColeEtAl-9] 콜 등 2000년.

[Cole-10] 콜 2000

[Tarjan-11] 타잔 1985년

[Elmasry-12] 2004년 엘마스리

[Pettie-13] Pettie 2008.

[Sundar-14] 순다르 1992년

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

v t 트리 데이터 구조
트리 검색 (다이나믹 세트/어소시에이션 어레이)	2–3 2–3–4 AA (a, b) AVL B B+ B* B^x. (최적) 바이너리 검색 춤추다 HTree 간격 주문통계 (좌향) 레드-블랙 희생양 스플라이 T 나무 UB 무게 밸런스
수북이	바이너리 이항 브로달 피보나치 좌파 페어링 스큐 판 엠데 보아스 약한
시도하다	Ctrie C-trie(압축 ADT) 해시 기수 서픽스 삼진수 검색 X-Fast 고속
공간 데이터 파티션 트리	공 BK BSP 데카르트어 힐베르트 R k-d(표준 k-d) M 미터법 MVP 옥트리 PH 우선 순위 R 쿼드 R R+ R* 부분 부사장 X
기타 트리	덮다 지수 펜윅 손가락. 프랙탈 트리 인덱스 퓨전 해시 캘린더 i디스턴스 K-ary 좌측자녀 우측자매 링크/컷 로그 구조화 결합 머클 p q. 범위 SPQR 정상

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

스플레이 트리

네임스페이스

더

목차

이점

단점들

운용

스플라이잉

합류하다

분열되다

삽입

삭제

구현 및 변형

분석.

지그 스텝

지그재그 스텝

지그재그 스텝

가중 분석

퍼포먼스 정리

동적 최적성 추측

변종

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

Search

스플레이 트리

이점

단점들

운용

스플라이잉

합류하다

분열되다

삽입

삭제

구현 및 변형

분석.

지그 스텝

지그재그 스텝

지그재그 스텝

가중 분석

퍼포먼스 정리

동적 최적성 추측

변종

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

「」를 참조해 주세요.