GOST(블록 암호)

GOST (block cipher)
GOST 28147-89 (매그마)
GOSTDiagram.png
GOST의 그림
일반
디자이너소련, KGB, 제8부
초판1994-05-23 (비밀 해제)
후계자GOST 해시 함수, Kuznyechik
인정.GOST 표준
암호 상세
키 사이즈256 비트
블록 크기64비트
구조.파이스텔 네트워크
라운드32

GOST 블록암호(Magma)는 표준 GOST 28147-89(RFC 5830)에 정의되어 있으며 블록사이즈가 64비트인 소련 및 러시아 정부의 표준 대칭키 블록암호입니다.1989년에 발표된 원래의 표준에서는 암호에 어떠한 이름도 붙이지 않았지만, 최신 개정판인 GOST R 34.12-2015(RFC 7801, RFC 8891)에서는 암호는 [1]마그마라고 불리고 있습니다.GOST 해시 함수는 이 암호에 기초하고 있습니다.새로운 표준은 또한 Kuznyechik이라고 불리는 새로운 128비트 블록 암호를 지정합니다.

1970년대에 개발된 이 표준은 "일급비밀"로 표기된 후 1990년에 "비밀"로 강등되었다.구소련이 해체된 지 얼마 되지 않아 기밀 해제되어 1994년에 일반에 공개되었다.GOST 28147은 미국 표준 알고리즘인 [2]DES의 소련 대체품이었다.따라서, 그 둘은 구조가 매우 유사하다.

알고리즘

GOST의 블록사이즈는 64비트이고 키 길이는 256비트입니다.S박스는 비밀일 수 있으며 약2 354비트(16!)8의 비밀정보를 포함하고 있기 때문에 유효키 사이즈를 610비트로 늘릴 수 있습니다.다만, 선택 키 공격에 의해서, 약32 2개의 암호화로 [3]S박스의 내용을 회복할 수 있습니다.

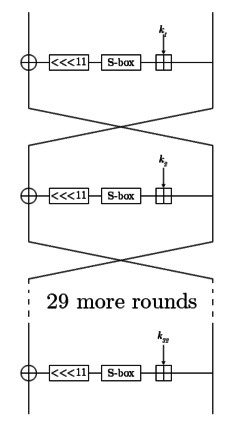
GOST는 32라운드의 Feistel 네트워크입니다.라운드 기능은 매우 간단합니다: 32비트 서브키 모듈로32 2를 추가하고 결과를 S박스 층에 넣은 후 결과를 왼쪽으로 11비트 회전시킵니다.그 결과 라운드 함수의 출력이 됩니다.인접한 그림에서 1개의 선은 32비트를 나타냅니다.

서브키는 미리 지정된 순서로 선택됩니다.키 스케줄은 매우 간단합니다.256비트키를 32비트 서브키 8개로 분할하여 각 서브키를 알고리즘으로 4회 사용합니다.첫 번째 24라운드는 키워드를 순서대로 사용하고 마지막 8라운드는 키워드를 역순으로 사용합니다.

S박스는 4비트 입력을 받아 4비트 출력을 생성합니다.라운드 기능의 S박스 대체는 8개의 4 × 4 S박스로 구성된다.S박스는 구현에 따라 다르므로 GOST를 사용하여 통신을 보호하려는 당사자는 동일한 S박스를 사용해야 합니다.보안을 강화하기 위해 S박스는 비밀로 할 수 있습니다.GOST가 지정된 원래 규격에서는 S박스가 제공되지 않았지만 어떻게든 공급되어야 했다.이 때문에 정부가 염탐하려는 조직에 약한 S박스가 주어졌다는 추측이 나왔다.한 GOST 칩 제조업체는 의사 난수 발생기를 [4]사용하여 직접 S박스를 생성했다고 보고했습니다.

예를 들어, 러시아 연방 중앙은행은 다음과 같은 S박스를 사용했습니다.

# S박스
1 4 A 9 2 D 8 0 E 6 B 1 C 7 F 5 3
2 E B 4 C 6 D F A 2 3 8 1 0 7 5 9
3 5 8 1 D A 3 4 2 E F C 7 6 0 9 B
4 7 D A 1 0 8 9 F E 4 6 C B 2 5 3
5 6 C 7 1 5 F D 8 4 A 9 E 0 3 B 2
6 4 B A 0 7 2 1 D 3 6 8 5 C F E
7 DB 4 1 3 F 5 9 0 A E 7 6 8 2 C
8 1 F D 0 5 7 A 4 9 2 3 E 6 B 8 C

그러나 최신 개정판 GOST R 34.12-2015에서는 누락된 S-box 사양을 추가하여 다음과 [1]같이 정의하고 있습니다.

# GOST R 34.12-2015 S박스
1 C 4 6 2 A 5 B 9 E 8 D 7 0 3 F 1
2 6 8 2 3 9 A 5 C 1 E 4 7 B D 0 F
3 B 3 5 8 2 F A D E 1 7 4 C 9 6 0
4 C 8 2 1 D 4 F 6 7 0 A 5 3 E 9 B
5 7 F 5 A 8 1 6 D 0 9 3 E B 4 2 C
6 5 D F 6 9 2 C A 7 8 1 4 3 E 0
7 8 E 2 5 6 9 1 C F 4 B 0 D A 3 7
8 1 7 E D 0 5 8 3 4 F A 6 9 C B 2

GOST의 암호화

GOST의 최신 암호화는 이론적으로 안전한 것으로 나타났습니다.실제로 가장 잘 공개된 공격의 데이터와 메모리의 복잡성은 실제 수준에 도달한 반면, 가장 잘 공개된 공격도 2개의 데이터를 사용할 수 있을64 때 시간의 복잡성은 여전히192 2개입니다.

2007년 이후 축소된 GOST 구현 및/또는 취약한 [5][6]키에 대한 공격이 여러 차례 개발되었습니다.

2011년에 여러 저자가 GOST에서 더 중요한 결함을 발견하여 처음으로 32라운드 GOST 전체를 임의의 키로 공격할 수 있게 되었습니다.심지어 니콜라 [7]쿠르투아는 이것을 "심각한 결함이 있는 암호"라고 불렀습니다.초기 공격은 엄청난 메모리 [8]요건을 희생시키면서 시간의 복잡성을 2개에서256 2개로 줄일228 수 있었고, 곧 2개의 메모리 및64 [9][10]2개의 데이터 비용으로70 복잡성이 최대 2개까지178 개선되었습니다.

2012년 12월 Courtois, Gawinecki 및 Song은 GOST 라운드를 [11]2회만101 계산하여 GOST에 대한 공격을 개선했습니다.Isobe는 이미 GOST [12]암호에 대한 단일 키 공격을 발표했으며, Dinur, Dunkelman 및 Shamir는 이를 개선하여 2개의 데이터와36 [13]2개의 메모리에 대해 2배의3264 복잡도에 도달했습니다224192.

공격은 예상 강도를 2(키 길이)에서256 약178 2로 낮추기 때문에 암호는 깨진 것으로 간주할 수 있습니다.단, 블록사이즈가 n비트인 모든 블록암호에서는 생일 [14]패러독스에 의해 키 재생성을 수행하기 전에 암호화할 수 있는 플레인텍스트의 최대량은 2블록이며n/2, 앞서 말한 공격 중 2개 미만의32 데이터가 필요한 것은 없습니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b "GOST R 34.12-2015 (Russian only)" (PDF). Archived from the original (PDF) on 2015-09-24. Retrieved 2015-08-28.
  2. ^ Fleischmann, Ewan; Gorski, Michael; Hühne, Jan-Hendrik; Lucks, Stefan (2009). "Key Recovery Attack on Full GOST Block Cipher with Zero Time and Memory". Published as ISO/IEC JTC. 1.
  3. ^ Saarinen, Markku-Juhani (1998). "A chosen key attack against the secret S-boxes of GOST". We show that a simple "black box" chosen-key attack against GOST can recover secret S-boxes with approximately 2^32 encryptions {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
  4. ^ Schneier, Bruce (1996). Applied cryptography : protocols, algorithms, and source code in C (2. ed., [Nachdr.] ed.). New York [u.a.]: Wiley. ISBN 978-0-471-11709-4.
  5. ^ Eli Biham; Orr Dunkelman; Nathan Keller (2007). "Improved Slide Attacks" (PDF).
  6. ^ Orhun Kara (2008). "Reflection Cryptanalysis of Some Ciphers".
  7. ^ Courtois, Nicolas T. (9 May 2011). "Security Evaluation of GOST 28147-89 In View Of International Standardisation". Cryptology ePrint Archive. IACR. Until 2011 researchers unanimously agreed that GOST could or should be very secure, which was summarised in 2010 in these words: despite considerable cryptanalytic efforts spent in the past 20 years, GOST is still not broken". Unhappily, it was recently discovered that GOST can be broken and is a deeply flawed cipher
  8. ^ Nicolas T. Courtois; Michał Miształ (2011). "Differential Cryptanalysis of GOST". IACR.
  9. ^ Nicolas T. Courtois (2012). "An Improved Differential Attack on Full GOST" (PDF). IACR.
  10. ^ Courtois, Nicolas T. (Jun 13, 2011). "Algebraic Complexity Reduction and Cryptanalysis of GOST" (PDF). Cryptology ePrint Archive. IACR.
  11. ^ Nicolas T. Courtois; Jerzy A. Gawinecki; Guangyan Song (2012). "CONTRADICTION IMMUNITY AND GUESS-THEN-DETERMINE ATTACKS ON GOST" (PDF). Versita. Retrieved 2014-08-25.
  12. ^ Isobe, Takanori (2011). "A Single-Key Attack on the Full GOST Block Cipher". Fast Software Encryption. Lecture Notes in Computer Science. Vol. 6733. pp. 290–305. doi:10.1007/978-3-642-21702-9_17. ISBN 978-3-642-21701-2.
  13. ^ Dinur, Itai; Dunkelman, Orr; Shamir, Adi (2012). "Improved Attacks on Full GOST". Lecture Notes in Computer Science. 7549 (Fast Software Encryption): 9–28. doi:10.1007/978-3-642-34047-5_2.
  14. ^ "Draft of ISO/IEC JTC 1/SC 27 Standing Document No. 12 (SD12) on the Assessment of Cryptographic Techniques and Key Lengths, 4th edition" (PDF). 2016.

추가 정보

외부 링크