소형 암호화 알고리즘

Tiny Encryption Algorithm
티
TEA InfoBox Diagram.png
티아 파이스텔[1] 라운드 2회(1사이클)
일반
디자이너로저 니덤, 데이비드 휠러
초판1994
후계자XTEA
암호 상세
키 사이즈128비트
블록 크기64비트
구조.파이스텔 네트워크
라운드가변, 64 Feistel 라운드 권장(32 사이클)
최고의 퍼블릭 암호 분석
TEA는 동등한 키에 시달리고 있으며(텍스트; 켈시 등, 1996 참조), 선택된 2개의 평문과 [2]2의32 시간 복잡도를 필요로23 하는 관련 키 공격을 사용하여 해독할 수 있다.표준 단일 비밀 키 설정에서 TEA의 가장 좋은 구조 암호 해독은 완전한 코드 북보다 적은 2회에 걸쳐121.5 21라운드를 돌파하는 제로 상관 암호 분석입니다.

암호학에서 Tiny Encryption Algorithm(TEA; 작은 암호화 알고리즘)은 일반적으로 몇 줄의 코드와 같은 간단한 설명과 구현으로 유명한 블록 암호입니다.Cambridge Computer Laboratory의 David Wheeler와 Roger Needham에 의해 설계되었으며, 1994년 Leuven에서 열린 Fast Software Encryption 워크숍에서 처음 발표되었으며,[4] 이 워크숍에서 처음 발표되었습니다.

암호는 특허의 대상이 아닙니다.

특성.

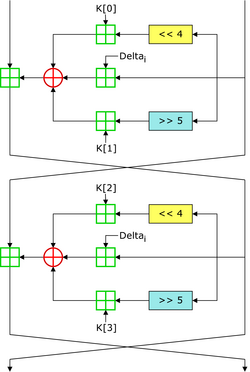
TEA는 2개의 32비트 부호 없는 정수(64비트 데이터 블록에서 파생될 수 있음)로 동작하며 128비트키를 사용합니다.64라운드를 권장하는 파이스텔 구조로 되어 있으며, 일반적으로 사이클이라고 불리는 쌍으로 구현됩니다.모든 주요 재료를 각 사이클에 대해 정확히 동일한 방식으로 혼합하는 매우 간단한 키 스케줄을 가지고 있습니다.라운드 대칭을 기반으로 한 단순한 공격을 방지하기 위해 서로 다른 매직 상수의 배수가 사용됩니다.매직 상수 2654435769 또는 0x9E3779B9는 '232/'로 선택됩니다.여기서 '는 황금비율(Nothing-up-my-slet 수치로서)[4]입니다.

TEA에는 몇 가지 단점이 있습니다.특히 각 키는 다른 3개의 키와 동일하기 때문에 유효한 키 [5]사이즈는 126비트밖에 되지 않습니다.그 결과 TEA는 암호화 해시함수로서 특히 좋지 않습니다.이 약점은 마이크로소프트의 Xbox 게임기를 해킹하는 방법으로 이어졌고, 이 암호는 해시 [6]함수로 사용되었다.또한 TEA는 관련 키 쌍에서 2개의 선택된 평문을 필요로23 하는 관련 키 공격에 취약하며 시간이32 [2]2개 복잡합니다.이러한 약점으로 인해 XTEA 암호는 설계되었습니다.

버전

TEA의 첫 번째 공개 버전은 보안을 강화하기 위해 확장을 도입한 두 번째 버전으로 보완되었습니다.블록 TEA(XTEA와 함께 지정됨)는 원래 64비트 블록 대신 임의의 크기의 블록으로 작동합니다.

1998년에 발표된 세 번째 버전(XXTEA)에서는 Block TEA 알고리즘의 보안을 강화하기 위한 추가 개선 사항을 설명했습니다.

참조코드

다음은 David Wheeler와 Roger Needham에 [4]의해 공개 도메인에 공개된 C의 참조 암호화 및 복호화 루틴을 수정한 것입니다.

#실패하다 < stdint >h>  무효 암호화 (uint32_t v[2], 컨스턴트 uint32_t k[4]) {     uint32_t v0=v[0], v1=v[1], 합=0, i;           /* 셋업 */     uint32_t 델타=0x9E3779B9;                     /* 주요 일정 상수 */     uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* 캐시 키 */     위해서 (i=0; i< >32; i++) {                         /* 기본 사이클 시작 */         합 += 델타;         v0 += ((v1<< >4) + k0) ^ (v1 + 합) ^ ((v1>>5) + k1);         v1 += ((v0<< >4) + k2) ^ (v0 + 합) ^ ((v0>>5) + k3);     }                                              /* 종료 사이클 */     v[0]=v0; v[1]=v1; }  무효 복호화 (uint32_t v[2], 컨스턴트 uint32_t k[4]) {     uint32_t v0=v[0], v1=v[1], 합=0xC6EF3720, i;  /* 설정; 합계는 (델타 < 5) & 0xFFFFFF */     uint32_t 델타=0x9E3779B9;                     /* 주요 일정 상수 */     uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* 캐시 키 */     위해서 (i=0; i< >32; i++) {                         /* 기본 사이클 시작 */         v1 -= ((v0<< >4) + k2) ^ (v0 + 합) ^ ((v0>>5) + k3);         v0 -= ((v1<< >4) + k0) ^ (v1 + 합) ^ ((v1>>5) + k1);         합 -= 델타;     }                                              /* 종료 사이클 */     v[0]=v0; v[1]=v1; }

참조 실장은 멀티바이트 수치로 동작합니다.원본 문서에서는 이진수 또는 기타 내용에서 어떻게 동작하는 숫자를 도출하는지에 대해 명시되어 있지 않습니다.

「 」를 참조해 주세요.

  • RC4 – TEA와 마찬가지로 구현이 매우 간단하도록 설계된 스트림 암호입니다.
  • XTEA – Block TEA의 후속 버전 첫 번째 버전입니다.
  • XXTEA – Block TEA의 후속 버전 수정.
  • 트레이퍼 – 심플하고 콤팩트한 암호화 알고리즘으로 64비트의 키 사이즈와 블록 사이즈를 갖추고 있습니다.

메모들

  1. ^ Matthew D. Russell (27 February 2004). "Tinyness: An Overview of TEA and Related Ciphers". Archived from the original on 12 August 2007.
  2. ^ a b Kelsey, John; Schneier, Bruce; Wagner, David (1997). Related-key cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X NewDES, RC2, and TEA. Lecture Notes in Computer Science. Vol. 1334. pp. 233–246. CiteSeerX 10.1.1.35.8112. doi:10.1007/BFb0028479. ISBN 978-3-540-63696-0.
  3. ^ Bogdanov, Andrey; Wang, Meiqin (2012). Zero-Correlation Linear Cryptanalysis with Reduced Data Complexity (PDF). Lecture Notes in Computer Science. Vol. 7549. Fast Software Encryption 2012. pp. 29–48. doi:10.1007/978-3-642-34047-5_3. ISBN 978-3-642-34046-8.
  4. ^ a b c Wheeler, David J.; Needham, Roger M. (16 December 1994). TEA, a tiny encryption algorithm. Lecture Notes in Computer Science. Vol. 1008. Leuven, Belgium: Fast Software Encryption: Second International Workshop. pp. 363–366. doi:10.1007/3-540-60590-8_29. ISBN 978-3-540-60590-4.
  5. ^ Kelsey, John; Schneier, Bruce; Wagner, David (1996). Key-schedule cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES (PDF). Lecture Notes in Computer Science. Vol. 1109. pp. 237–251. doi:10.1007/3-540-68697-5_19. ISBN 978-3-540-61512-5.
  6. ^ Michael Steil. "17 Mistakes Microsoft Made in the Xbox Security System". Archived from the original on 16 April 2009.

레퍼런스

외부 링크