측지 다면체

{3,5+}_6,0에 대한 3개의 구성




삼각형 면을 더 작은 삼각형으로 나누고 모든 새로운 정점을 구에 투영함으로써 높은 지오데틱 다면체를 정의하는 데 이코사면체와 관련 대칭 다면체를 사용할 수 있다.고차 다각형 면은 각 면 중심의 새로운 정점을 추가하여 삼각형으로 나눌 수 있다.구체의 새로운 면은 등변 삼각형이 아니라 대략 가장자리 길이가 같다.모든 정점은 valence-5인 12 정점을 제외한 valence-6이다.

{3,5+}_3,3 건설


지리학적 세분화는 또한 오구체화된 도데카헤드론에서 수행될 수 있으며, 펜타곤을 중심점이 있는 삼각형으로 나누고, 그것으로부터 세분화한다.

{3,5+}_6,3 건설


고차 다각형 면이 있는 치랄 다면체는 중앙점과 새로운 삼각형 면으로 증강할 수 있다.그 삼각형들은 새로운 지질학적 다면체를 위해 더 작은 삼각형으로 세분될 수 있다.모든 정점은 Valence-5인 원래 정점에 중심을 맞춘 12개를 제외하고 valence-6이다.

혼합지오데틱 형태 구축

지오데틱 세분화는 또한 증원된 사각형 면에 의해 수행될 수 있지만, 결과 삼각형은 정삼각형이 아니라 정삼각형 근처에 있을 것이다.이 Rhombicosidodechadron의 예는 각 꼭지점 주위에 4~7개의 삼각형을 가지고 있다.

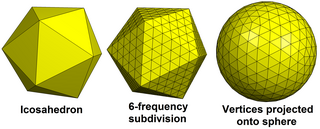
지질 다면체(geodesic polyhedron)는 삼각형으로 만들어진 볼록 다면체다.그들은 보통 정점에 6개의 삼각형이 있는 등, 5개의 삼각형이 있는 정점 12개를 제외하고, 이등면 대칭을 가지고 있다.대부분 육각형의 얼굴을 가진 해당 골드버그 폴리헤드라(Goldberg Polyheadra)의 듀얼이다.

지오데식 다면체는 여러 가지 목적을 위한 구에 대한 좋은 근사치로, 여러 가지 다른 맥락에서 나타난다.가장 잘 알려진 것은 버크민스터 풀러가 설계한 지오디컬 돔일 수 있는데, 지오디컬 다면체의 이름을 따서 지오디컬 돔이라고 한다.지오데이에 사용되는 지오데틱 그리드는 지오데틱 다면체의 기하학적 구조도 가지고 있다.일부 바이러스의 캡시드는 지오데틱 폴리헤드라의 모양을 하고 있으며,^[1]^[2] 풀레렌 분자는 골드버그 폴리헤드라의 모양을 하고 있다.지오데틱 다면체는 ICosper라고 불리는 블렌더 3D 모델링 소프트웨어 패키지에서 기하학적 원시성으로 이용 가능하다. 그들은 UV 구에 대한 대안으로서 UV 구보다 정점 분포가 더 규칙적이다.^[3]^[4]Goldberg-Coxeter 구조는 지질 다면체의 기초가 되는 개념의 확장이다.

지오데틱 표기법

Magnus Wenninger의 구형 모델에서 다면체에는 {3,q+}_b,c 형식의 지오데틱 표기법이 부여되며, 여기서 {3,q}은 삼각형 면과 q-valance 정점을 가진 일반 다면체의 Schléfli 기호다.+ 기호는 정점이 증가하는 valence를 나타낸다. b,c는 하위분할 설명을 나타내며, 1,0은 기본 형태를 나타낸다.형태에는 3가지 대칭 등급이 있다: 사면체에는 {3,3+},_1,0 팔면체에는 {3,4+},_1,0 이면체에는 {3,5+}._1,0

골드버그 폴리헤드라의 이중 표기법은 valence-3 정점을 가진 {q+,3}_b,c이며, q-곤과 육각면이다.형태에는 3가지 대칭 등급이 있다: 사면체에는 {3,3},_1,0 큐브에는 {4+,3},_1,0 도면체에는 {5+,3}._1,0

b,c에 대한 값은 세 가지 등급으로 나뉜다.

클래스 I(b=0 또는 c=0): {3,q+}_b,0 또는 {3,q+}_0,b은(는) 원래 가장자리가 b 하위 에지로 분할되는 단순한 분할을 나타낸다.

클래스 II(b=c): {3,q+}_b,b은(는) q-곤면 이중 다면 {q,3}에서 먼저 중심점이 있는 삼각형으로 나눈 다음 모든 가장자리를 b 하위 에지로 나눈다.

클래스 III: {3,q+}_b,c은(는) b,c에 대해 0이 아닌 불평등 값을 가지며, 키랄 쌍으로 존재한다.b > c에 대해서는 오른손잡이의 형태로 정의할 수 있으며, c > b는 왼손잡이의 형태다.

여기서 등급3의 세분류는 단순히 원래의 가장자리에 정렬하지 않는다.서브그리드들은 한 방향으로 한 꼭지점 b 스텝에서 격자 정점과 보행로 위에 큰 삼각형을 위치시키고, 시계방향 또는 반시계방향으로 한 바퀴 돌고, 그리고 다음 1차 정점으로 다른 c 스텝을 배치하는 삼각형 타일링을 보고 추출할 수 있다.

예를 들어, 이코사면체는 {3,5+}_1,0이고 펜타키스 도데면체 {3,5+}_1,1은 5개의 삼각형으로 나뉘어진 오각형의 얼굴을 가진 일반 도데면체로 보인다.

구획의 1차 면을 주 다면 삼각형(PPT) 또는 고장 구조라고 한다.단일 PPT를 계산하면 전체 수치가 생성될 수 있다.

지오데믹 다면체의 주파수는 + = b + c의 합으로 정의된다. 고조파는 ν = 2b이므로 ν의 모든 분위가 될 수 있다. 클래스 II는 항상 2의 고조파를 가진다.

삼각측량 번호는 T = b + bc² + c이다².이 숫자의 원래 면의 수는 새 다면체의 삼각형 수를 나타낸다.

**주파수 8의 PPT**

요소들

원소의 수는 $T=b^{2}+bc+c^{2}$ = $T=b^{2}+bc+c^{2}$ $T=b^{2}+bc+c^{2}$ + b $T=b^{2}+bc+c^{2}$ + c + $T=b^{2}+bc+c^{2}$ 2 ${\$ 두 개의 다른 지오데믹 다면체는 동일한 수의 원소를 가질 수 있다 $T=b^{2}+bc+c^{2}$ 예를 들어, {3,5+}_5,3 및 {3,5+}_7,0는 모두 T=49를 가지고 있다.

대칭	이코사헤드랄	팔면체	사면체
베이스	이코사헤드론 {3,5} = {3,5+}_1,0	팔면체 {3,4} = {3,4+}_1,0	사면체 {3,3} = {3,3+}_1,0
이미지
기호	{3,5+}_b,c	{3,4+}_b,c	{3,3+}_b,c
정점	$10T+2$	$(\디스플레이 스타일 4T+2})$	$2T+2$
얼굴	$(\디스플레이 스타일 20T)$	$8T}$	$(\displaystyle 4T)$
가장자리	$(\디스플레이 스타일 30T)$	$(\displaystyle 12T)$	$(\디스플레이 스타일 6T)$

건설

지오데식 다면체는 보다 단순한 다면체의 면을 세분화한 다음 새로운 정점을 구의 표면에 투영하는 방식으로 구성된다.지오데틱 다면체는 구에 근접한 직선 가장자리와 평면을 가지지만 구면 및 구면 삼각면 표면에 진정한 지오데틱 곡선 가장자리가 있는 구형 다면체(구면 테셀레이션)로도 만들 수 있다.

콘웨이	u₃I = (kt)i	(k)tI	ktI
이미지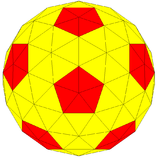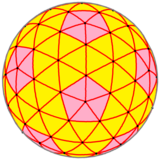
형태	3주파수 세분화된 이도사면체	키스가 잘린 이코사면체	측지 다면체(3,0)	구면 다면체

이 경우 주파수 $\nu =3$ = $\nu =3$ $\nu =3$ 및 삼각측량 $\nu =3$ $T=9$ T $T=9$ = 9 $T=9$ 을 $T=9$ 를) 갖는 {3,5+},_3,0 폴리곤의 4가지 버전은 각각 92개의 꼭지점(가장자리 6개가 결합하는 80개, 5개가 결합하는 12개), 270개의 가장자리와 180면을 가진다.

골드버그 폴리헤드라와의 관계

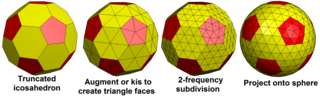
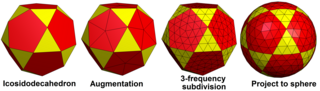
Geodesic Polyedra는 Goldberg Polyedra의 이중이다.골드버그 폴리헤드라(Goldberg Polyedra)는 키스 연산자(중앙점과 면 삼각형을 나누면)를 적용하면 새로운 지오데틱 폴리헤드라가 생성되고, 지오데틱 폴리헤드론의 정점을 잘라내면 새로운 골드버그 폴리헤드론이 생성된다는 점에서도 관련이 있다.예를 들어, 골드버그 G(2,1)의 kized, {3,5+}_4,1이(가) 되고, G(6,3)이 되는 잘림 현상이 나타난다.그리고 비슷하게 {3,5+}_2,1이(가) 잘리면 G(4,1)가 되고, 그 kized는 {3,5+}_6,3이(가) 된다.

예

1급

1급 지오데틱 다면체
빈도	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	(m,0)
T	1	4	9	16	25	36	49	64	m²
면 삼각형의									...
이코사헤드랄									더 많은
팔면체								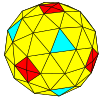	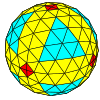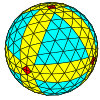더 많은
사면체									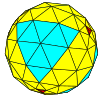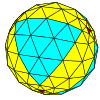더 많은

클래스 II

II급 지오데틱 다면체
빈도	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	(m,m)
T	3	12	27	48	75	108	147	192	3m²
면 삼각형의									...
이코사헤드랄								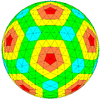	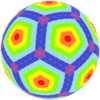더 많은
팔면체									더 많은
사면체									더 많은

3급

3급 지오데틱 다면체
빈도	(2,1)	(3,1)	(3,2)	(4,1)	(4,2)	(4,3)	(5,1)	(5,2)	(m,n)
T	7	13	19	21	28	37	31	39	m²+mn+n²
면 삼각형의									...
이코사헤드랄									더 많은
팔면체									더 많은
사면체									더 많은

구면 모형

Magnus Wenninger의 책 "구면 모델"은 다면체 모델을 제작할 때 이러한 세분화를 탐구한다.이 모델들의 구조를 설명한 후, 그는 패턴을 표시하기 위해 삼각망 사용을 설명했는데, 삼각망은 모델에서 색칠되거나 제외되었다.^[5]

예제 모델
마그누스 웬닝거 신부가 만든 예술적 모델 혼돈의 질서라고 불리는 것으로, 16주파수 이코사헤드랄 지오데시스 구체의 치랄 부분집합, {3,5+}_16,0	이두각 대칭 원들을 보여주는 가상 복사본.6배 회전 대칭은 환상적이며, 이코사헤드론 자체에 존재하지 않는다.	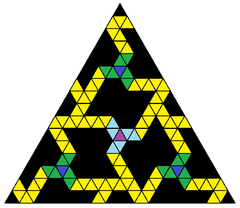16주파수분할이 있는 단일한 이두면 삼각형

참고 항목

콘웨이 다면체 표기법

참조

^ Caspar, D. L. D.; Klug, A. (1962). "Physical Principles in the Construction of Regular Viruses". Cold Spring Harb. Symp. Quant. Biol. 27: 1–24. doi:10.1101/sqb.1962.027.001.005. PMID 14019094.
^ Coxeter, H.S.M. (1971). "Virus macromolecules and geodesic domes.". In Butcher, J. C. (ed.). A spectrum of mathematics. Oxford University Press. pp. 98–107.
^ "Mesh Primitives", Blender Reference Manual, Version 2.77, retrieved 2016-06-11.
^ "What is the difference between a UV Sphere and an Icosphere?". Blender Stack Exchange.
^ 구면 모형, 페이지 150-159

로버트 윌리엄스 자연 구조의 기하학적 기초: 디자인 출처, 1979, 페이지 142–144, 그림 4-49,50,51 12개의 구, 42개의 구, 92개의 구를 가진 고객
안토니우스 푸그, 폴리헤드라: 시각적 접근, 1976년 6장.R의 지오데틱 폴리헤드라.벅민스터 풀러 및 관련 폴리헤드라
Wenninger, Magnus (1979), Spherical Models, Cambridge University Press, ISBN 978-0-521-29432-4, MR 0552023, archived from the original on July 4, 2008 도버 1999 ISBN 978-0-486-40921-4
에드워드 S.Popko, Divided spheres: Geodesics & the Orderly Subdivision of the Sphere (2012) Chapter 8 Subdivision schemas, 8.1 Geodesic Notation, 8.2 Triangulation number 8.3 Frequency and Harmonics 8.4 Grid Symmetry 8.5 Class I: Alternates and fords 8.5.1 Defining the Principal triangle 8.5.2 Edge Reference Points

[Caspar1962-1] Caspar, D. L. D.; Klug, A. (1962). "Physical Principles in the Construction of Regular Viruses". Cold Spring Harb. Symp. Quant. Biol. 27: 1–24. doi:10.1101/sqb.1962.027.001.005. PMID 14019094.

[2] Coxeter, H.S.M. (1971). "Virus macromolecules and geodesic domes.". In Butcher, J. C. (ed.). A spectrum of mathematics. Oxford University Press. pp. 98–107.

[3] "Mesh Primitives", Blender Reference Manual, Version 2.77, retrieved 2016-06-11.

[4] "What is the difference between a UV Sphere and an Icosphere?". Blender Stack Exchange.

[5] 구면 모형, 페이지 150-159

[1]

[2]

[3]

[4]

[5]

Search