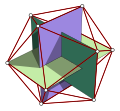
깎은 20면체

Truncated icosahedron
깎은 20면체
Truncatedicosahedron.jpg
(회전 모델을 보려면 여기를 클릭)
유형 아르키메데스의 입체
균일한 다면체
요소들 F = 32, E = 90, V = 60 (표준 = 2)
측면 나란히 12{5}+20{6}
콘웨이 표기법 tI
슐레플리 기호 t{3,5}
t0,1{3,5}
위토프 기호 2 5 3
콕서터 다이어그램 CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png
대칭군 Ih, H3, [5,3], (*532), 120 주문
로테이션 그룹 I, [5,3],+ (532), 주문 60
이면각 6-6: 138.189685°
6-5: 142.62°
레퍼런스 U25, C27, W9
특성. 반규칙 볼록
Polyhedron truncated 20 max.png
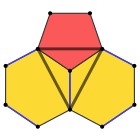유색인종		 Polyhedron truncated 20 vertfig.svg
5.6.6
(버텍스 그림)
Polyhedron truncated 20 dual max.png
펜타키스 12면체
(입체 다면체)		 Polyhedron truncated 20 net compact.svg
그물

기하학에서, 잘린 20면체는 아르키메데스의 고체이며, 32개의 면이 두 개 이상의 정다각형인 13개의 볼록한 등각 비프리스마틱 고체 중 하나이다.이러한 도형 중 삼각형이나 정사각형이 포함되지 않은 유일한 도형입니다.일반적으로, 잘라내는 정도는 지정이 없는 한 균일한 것으로 간주됩니다.

그것은 12개의 정오각형 면, 20개의 정육각형 면, 60개의 정점과 90개의 모서리를 가지고 있다.

그것은 오각형과 육각형 면을 포함하는 골드버그 다면체V GP(1,1) 또는 {5+,1,13}입니다.

이 지오메트리는 일반적으로 흰색 육각형과 검은색 펜타곤으로 패턴화된 축구공(축구공)과 관련이 있습니다.Buckminster Fuller가 개척한 건축물과 같은 측지학적 돔은 종종 이 구조에 기초한다.이것은 또한 풀러렌60 C("버키볼") 분자의 기하학과도 일치합니다.

이것은 세포 전이 쌍곡선 공간 채우기 테셀레이션, 비트런치 순서 5 12면체 벌집형에서 사용됩니다.

건설

이십면체

이 다면체는 12개의 정점이 잘린(잘려나간) 20면체로 구성될 수 있으며, 각 모서리의 3분의 1이 양쪽 끝에서 잘립니다.그러면 12개의 새로운 오각형 면이 생성되고 원래 20개의 삼각형 면은 일반 육각형으로 남습니다.따라서 모서리의 길이는 원래 모서리의 1/3입니다.또한 모양은 1440개의 [citation needed]대각선이 있습니다.

특성.

기하학과 그래프 이론에는 몇 가지 표준 다면체 특성이 있습니다.

데카르트 좌표

원점을 중심으로 한 잘린 20면체의 꼭지점에 대한 데카르트 좌표는 모두 다음과 같은 짝수 배열입니다.

(0, ±1, ±3°)
(±1, ±(2 + µ), ±2µ)
(±440, ±2, ±(2°C + 1))

여기서 =은(는) =1 + ≤ 5/2는 황금 평균입니다.원둘레는 φ9 10 + 10 954.956 이며 가장자리의 길이는 [1]2 입니다.

직교 투영

잘린 20면체에는 정점을 중심으로 두 가지 유형의 모서리와 두 가지 유형의 면(육각형과 오각형)이 있는 5개의 특수 직교 돌출부가 있습니다.마지막 두 개는 A와22 H 콕서터 평면에 해당합니다.

직교 투영
중심 꼭지점 엣지
5-6		 엣지
6-6		 얼굴
육각형		 얼굴
펜타곤
단단한 Polyhedron truncated 20 from blue max.png Polyhedron truncated 20 from yellow max.png Polyhedron truncated 20 from red max.png
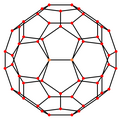와이어프레임 Dodecahedron t12 v.png Dodecahedron t12 e56.png Dodecahedron t12 e66.png Icosahedron t01 A2.png Icosahedron t01 H3.png
투사적
대칭		 [2] [2] [2] [6] [10]
듀얼 Dual dodecahedron t01 v.png Dual dodecahedron t01 e56.png Dual dodecahedron t01 e66.png Dual dodecahedron t01 A2.png Dual dodecahedron t01 H3.png

구면 타일링

잘린 20면체는 또한 구면 타일링으로 표현될 수 있으며 입체 투영을 통해 평면에 투영될 수 있습니다.이 투영법은 적합하며 각도는 보존되지만 면적이나 길이는 보존되지 않습니다.구면의 직선은 평면에 원형 호로 투영됩니다.

Uniform tiling 532-t12.png Truncated icosahedron stereographic projection pentagon.png
오각형 중심의		 Truncated icosahedron stereographic projection hexagon.png
육각형 중심의
맞춤법 투영법 입체 투영

치수

원래의 20면체로 그려진 상호 직교 황금 직사각형(절단 전)

잘린 20면체의 모서리 길이가 a인 경우, 외접구(모든 정점에서 잘린 20면체와 접촉하는 구)의 반지름은 다음과 같다.

여기서 θ는 황금비율입니다.

이 결과는 원래 20면체에 그려진 세 개의 직교 황금 직사각형 중 하나를 고려의 시작점으로 사용하면 쉽게 얻을 수 있습니다.중심을 연결하는 세그먼트와 공유 모서리로 연결된 정점 사이의 각도는 약 23.281446°입니다.

면적 및 볼륨

모서리 길이 a의 잘린 20면체의 면적 A와 부피 V는 다음과 같다.

단위 가장자리에서 표면적은 펜타곤의 경우 21, 육각의 경우 52이며, 함께 73(정다각형 영역 참조)이다.

잘린 20면체는 오일러 특성을 쉽게 보여줍니다.

32 + 60 − 90 = 2.

적용들

축구와 팀 핸드볼에서 사용되는 공은 아마도 일상 [2]생활에서 발견되는 잘린 20면체와 유사한 구면 다면체의 가장 잘 알려진 예일 것이다.공은 일반 펜타곤과 일반 헥사곤의 동일한 패턴으로 구성되지만, 내부 공기의 압력과 공의 탄성 때문에 더 구체적입니다.이 공 유형은 1970년에 월드컵에 도입되었습니다(2006년부터 이 상징적인 디자인은 대체 패턴으로 대체되었습니다).

축구장을 나타내는 영국 교통 표지판은 잘린 20면체 대신 균일하게 색상의 육각형 타일 부분을 사용해 축구공을 표현한다.이것은 수학자이자 코미디언인 매트 파커를 화나게 했고, 그는 영국 정부에 이 부호들을 기하학적으로 정확하게 바꿔달라고 청원하기 시작했다.그 청원은 결국 기각되었다.

지오데식 돔은 일반적으로 Buckminster [3]Fuller에 의해 널리 알려진 전 세계에서 발견된 구조물들과 함께 이 지오메트리의 삼각형 면을 기반으로 합니다.

이십면체의 변형은 1971년부터 1976년 사이에 폰티액 자동차 사업부에서 트랜스암과 [citation needed]그랑프리에서 사용한 벌집형 휠(폴리캐스트 소재로 제작)의 기초로 사용되었습니다.

이 모양은 또한 기폭장치와 팻맨 원자폭탄의 [4]폭발적 충격파에 초점을 맞추는 데 사용되는 렌즈의 구성이었다.

잘린 20면체는 또한 1985년에 발견된 원소 탄소의 동소체인 벅민스터 풀레렌(Flulerene) (C60) 또는 "버키볼" 분자의 모형으로 묘사될 수 있다.풋볼과 플라렌 분자의 직경은 각각 22cm, 약 0.71nm이므로 크기비는 31,000,000:1 이하이다.

대중 공예 문화에서는 20면체 패턴과 플라스틱, 스티로폼 또는 종이컵을 사용하여 큰 반짝이를 만들 수 있습니다.

예술에 있어서

관련 다면체

균일한 20면체 다면체군
대칭: [5,3], (*532) [5,3]+, (532)
Uniform polyhedron-53-t0.svg Uniform polyhedron-53-t01.svg Uniform polyhedron-53-t1.svg Uniform polyhedron-53-t12.svg Uniform polyhedron-53-t2.svg Uniform polyhedron-53-t02.png Uniform polyhedron-53-t012.png Uniform polyhedron-53-s012.png
CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png CDel node.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png CDel node h.pngCDel 5.pngCDel node h.pngCDel 3.pngCDel node h.png
{5,3} t{5,3} r{5,3} t{3,5} {3,5} rr{5,3} tr{5,3} sr {5,3}
이중에서 균일한 다면체
Icosahedron.jpg Triakisicosahedron.jpg Rhombictriacontahedron.jpg Pentakisdodecahedron.jpg Dodecahedron.jpg Deltoidalhexecontahedron.jpg Disdyakistriacontahedron.jpg Pentagonalhexecontahedronccw.jpg
V5.5.5 V3.10.10 V3.5.3.5 V5.6.6 V3.3.3.3 V3.4.5.4 V4.6.10 V3.3.3.5
*n32 잘린 타일링 대칭 돌연변이: n.6.6
Sym.
*n42
[n,3]		 구면 유클리드 작은 파라크 비콤팩트 쌍곡선
*232
[2,3]		 *332
[3,3]		 *432
[4,3]		 *532
[5,3]		 *632
[6,3]		 *732
[7,3]		 *832
[8,3]... 		*∞32
[∞,3]		 [12i, 3] [9i, 3] [6i, 3]
잘렸다
수치		 Hexagonal dihedron.svg Uniform tiling 332-t12.png Uniform tiling 432-t12.png Uniform tiling 532-t12.png Uniform tiling 63-t12.svg Truncated order-7 triangular tiling.svg H2-8-3-trunc-primal.svg H2 tiling 23i-6.png H2 tiling 23j12-6.png H2 tiling 23j9-6.png H2 tiling 23j-6.png
설정. 2.6.6 3.6.6 4.6.6 5.6.6 6.6.6 7.6.6 8.6.6 ∞.6.6 12i.6.6 9i.6.6 6i.6.6
n개
수치		 Hexagonal Hosohedron.svg Spherical triakis tetrahedron.png Spherical tetrakis hexahedron.png Spherical pentakis dodecahedron.png Uniform tiling 63-t2.svg Heptakis heptagonal tiling.svg H2-8-3-kis-dual.svg H2checkers 33i.png
설정. V2.6.6 V3.6.6 V4.6.6 V5.6.6 V6.6.6 V7.6.6 V8.6.6 V†.6.6 V12i.6.6 V9i.6.6 V6i.6.6

이 균일한 별 다면체와 하나의 정십면체 단면은 불균일하게 잘린 이코사면체 볼록한 선체를 가지고 있다.

잘린 정십면체 그래프

잘린 정십면체 그래프
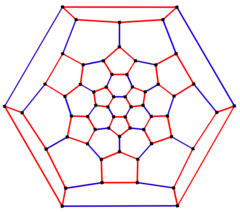Truncated icosahedral graph.png
6배 대칭 슐레겔도
꼭지점60
가장자리90
자기동형120
색수3
특성.입방체, 해밀턴, 정칙, 제로 대칭
그래프 및 매개 변수 표

그래프 이론의 수학 분야에서, 잘린 20면체 그래프는 아르키메데스의 고체 중 하나인 잘린 20면체의 꼭지점과 모서리의 그래프이다.60개의 꼭지점과 90개의 모서리가 있으며 입방체 아르키메데스 [5][6][7][8]그래프입니다.

맞춤법 투영법
Icosahedron t01 H3.png
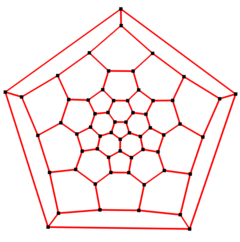5배 대칭		 Truncated icosahedral graph pentcenter.png
5배 슐레겔도

역사

피에로 델라 프란체스카의 저서 De quinque corposibus regular bus에 나오는 잘린 20면체 이미지

잘린 20면체는 아르키메데스에게 알려져 있었는데, 아르키메데스는 잃어버린 작품에서 13개의 아르키메데스 고형물을 분류했다.이 모양들에 대한 그의 연구는 알렉산드리아의 파푸스로부터 나온 것으로, 그는 단지 각각의 면의 수를 나열했을 뿐이다: 잘린 20면체의 경우, 12개의 5각형과 20개의 6각형.잘린 20면체의 첫 번째 이미지와 완전한 설명은 피에로 델라 프란체스카가 15세기 그의 책 De Quinque corpinibus regularbus에서 재발견한 것으로, 아르키메데스 다면체의 5개의 자른 부분들을 포함하고 있다.[9]레오나르도 다빈치가 1509년 루카 파치올리의 델라 프란체스카 책 표절 삽화에서 묘사한 것과 같은 형상이다.비록 알브레히트 뒤러가 다면체에 대한 그의 1525년 저서 Underweysung der Messung에 나열된 다른 아르키메데스의 고체에서 이 모양을 생략했지만, 그것에 대한 설명은 1538년에 출판된 그의 사후 논문에서 발견되었다.요하네스 케플러는 나중에 잘린 20면체를 포함한 13개의 아르키메데스 고체의 완전한 목록을 재발견하여 1609년 책인 하모니테스 [10]먼디에 포함시켰다.

「 」를 참조해 주세요.

메모들

  1. ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
  2. ^ Kotschick, Dieter (2006). "The Topology and Combinatorics of Soccer Balls". American Scientist. 94 (4): 350–357. doi:10.1511/2006.60.350.
  3. ^ Krebs, Albin (July 2, 1983). "R. Buckminster Fuller Dead; Futurist Built Geodesic Dome". The New York Times. New York, N.Y. p. 1. Retrieved 7 November 2021.
  4. ^ Rhodes, Richard (1996). Dark Sun: The Making of the Hydrogen Bomb. Touchstone Books. pp. 195. ISBN 0-684-82414-0.
  5. ^ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs. Oxford University Press. p. 268.
  6. ^ Weisstein, Eric W. "Truncated icosahedral graph". MathWorld.
  7. ^ Godsil, C. 및 Royle, G. 대수 그래프 이론 뉴욕: Springer-Verlag, 페이지 211, 2001
  8. ^ 코스탄트, B잘린 이십면체의 그래프와 갈로아의 마지막 글자.통지 Amer.수학, Soc. 42, 1995, 959-968 페이지 PDF
  9. ^ Katz, Eugene A. (2011). "Bridges between mathematics, natural sciences, architecture and art: case of fullerenes". Art, Science, and Technology: Interaction Between Three Cultures, Proceedings of the First International Conference. pp. 60–71.
  10. ^ Field, J. V. (1997). "Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler". Archive for History of Exact Sciences. 50 (3–4): 241–289. doi:10.1007/BF00374595. JSTOR 41134110. MR 1457069. S2CID 118516740.

레퍼런스

  • 윌리엄스, 로버트(1979년).그 기하학적 재단 자연 구조물의:소스 북 디자인도버 Publications, Inc.아이 에스비엔 0-486-23729-X.(섹션 3-9)
  • Cromwell, P. (1997). "Archimedean solids". Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468.

외부 링크

위키 낱말 사전, 자유 사전에들의 길이를 줄였다 20면체를 찾아 주세요.