콘웨이 다면체 표기법

기하학에서는 존 호튼 콘웨이가 발명하고 조지 W. 하트가 추진한 콘웨이 다면체 표기법은 다양한 접두사 연산에 의해 수정된 종자 다면체를 바탕으로 다면체를 기술하는 데 사용된다.^[1][2]

콘웨이와 하트는 케플러에 의해 정의된 잘림과 같은 연산자를 사용하여 같은 대칭의 관련 다면체를 구축하는 아이디어를 확장했다.예를 들어 tC는 잘린 입방체를 $나타내며{\displaystyle }$ t${\displaystyle }$(${\displaystyle C}$ ) ${\displaystyle$ t$(aC)}$로 구문 분석된 taC는 잘린 큐보타헤드론이다$.$가장 간단한 연산자 듀얼 스왑 정점 및 얼굴 요소. 예를 들어 듀얼 큐브는 8각형: dC=O.연속적으로 적용되는 이들 연산자는 많은 고차 다면체의 생성을 허용한다.콘웨이는 연산자를 abdegjkmost라고 정의했고, Hart는 r과 p를 추가했다.^[3]이후 구현에서는 추가 운영자를 명명했으며, 때로는 "확장" 운영자로 언급하기도 했다.^[4][5]콘웨이의 기본 작전은 플라토닉 고형물로부터 아르키메데스 고형물과 카탈루냐 고형물을 생성하기에 충분하다.일부 기본 연산은 다른 연산의 복합 재료로 만들 수 있다. 예를 들어, 두 번 적용된 암보는 확장 연산: aa = e, 암보 후 잘리면 베벨: ta = b.

다면체는 정점, 가장자리 및 얼굴이 어떻게 서로 연결되는지, 또는 기하학적으로 우주에 있는 원소의 배치 측면에서, 위상학적으로 연구될 수 있다.이러한 운영자의 서로 다른 구현은 기하학적으로 다르지만 위상적으로 동등한 다면체를 생성할 수 있다.이러한 위상학적으로 동등한 다면체들은 구에 다면체 그래프를 많이 내장시킨 것 중 하나로 생각할 수 있다.달리 명시되지 않는 한, 본 기사(및 일반적으로 콘웨이 운영자에 관한 문헌)에서 위상이 주요 관심사다.0속(즉, 지구상으로는 구와 동등한)을 가진 폴리헤드라는 모호성을 피하기 위해 표준적인 형태로 넣는 경우가 많다.

연산자

콘웨이의 표기법에서는 다면체에서의 연산을 오른쪽에서 왼쪽으로 함수와 같이 적용한다.For example, a cuboctahedron is an ambo cube,^[6] i.e. ${\displaystyle a(C)=aC}$, and a truncated cuboctahedron is ${\displaystyle t(a(C))=t(aC)=taC}$. Repeated application of an operator can be denoted with an exponent: j² = o.일반적으로 콘웨이 운영자는 서로 상통하지 않는다.

개별 연산자는 아래와 같이 기본 영역(또는 챔버)의 관점에서 시각화할 수 있다.각각의 오른쪽 삼각형은 기본적인 영역이다.각각의 하얀 방은 다른 방들의 회전된 버전이고, 각각의 색깔의 방도 그렇다.아치랄 연산자의 경우 색실(色室)은 백실(白室)의 반영이며, 모두 전이적이다.집단적 용어로, 아치랄 연산자는 dihedral 그룹 D에_n 대응하는데 여기서 n은 얼굴의 면의 수인 반면, chiral 연산자는 dihedral 그룹의 반사 대칭성이 결여된 순환 그룹 C에_n 대응한다.아치랄과 치랄 연산자를 각각 방향 보존 대칭(LOPSP)을 보존하는 국소 대칭 보존 연산(LSP)이라고도 한다.^[7][8][9]LSP는 국소 대칭을 보존하는 연산이 아니라 대칭을 보존하는 국소 연산으로 이해해야 한다.다시 말하지만 이것들은 기하학적 의미가 아니라 위상학적 의미에서 대칭이다: 정확한 각도와 가장자리 길이는 다를 수 있다.

$면$이 n ${\displaystyle n}$개인 면의 기본 도메인

3 (삼각형)	4 (제곱)	5 (펜타곤)	6 (헥사곤)
다면체 그룹의 기본 도메인.The groups are ${\displaystyle D_{3},D_{4},D_{5},D_{6}}$ for achiral polyhedra, and ${\displaystyle C_{3},C_{4},C_{5},C_{6}}$ for chiral polyhedra.

Hart는 다면체의 거울 이미지를 주는 반사 연산자 r을 소개했다.^[6]이것은 방향을 보존하지 않기 때문에 엄격하게 LOPSP가 아니다. 흰색과 빨간색 챔버를 교환함으로써 방향을 역전시킨다. r는 방향 외에 아치랄 다면체에 영향을 주지 않으며, rr = S는 원래의 다면체를 반환한다.오버라인은 연산자의 다른 키랄 형식을 나타내기 위해 사용될 수 있다: s = rsr.

d와 r을 제외하고 연산자의 구성으로 표현할 수 없는 경우, 연산은 되돌릴 수 없다.콘웨이의 원래 운영자의 대다수는 수정할 수 없다. 예외는 e, b, o, m이다.

행렬 표현

x	${\displaystyle {\begin{bmatrix}a&b&c\0&d&0\\a'&c'\end{bmatrix}=\mathbf{M} _{x}}}}}$
xd	${\displaystyle {\bematrix}c&a\0&d&0\\c&b'&a'\end{bmatrix}=\mathbf {M} _{d}}}$
dx	${\displaystyle {\begin{bmatrix}a'&b'&c'\0&d&0\\a&c\end{bmatrix}=\mathbf {M} _{x}}}}$
dxd	${\displaystyle {\begin}c'&b'&a'\\0&d&a\\c&d&a\end{bmatrix}=\mathbf {M}_{d}\mathbf {M} _{d}}}}$

이 글에 열거된 연산에 의해 생성된 다면체와 씨앗의 정점수, 가장자리, 면의 관계는 행렬 M ${\displaystyle {}_{}}$ ${\$로 표현할 수 있다$.$ x가 연산자일 때, $v{\displaystyle }$, ${\displaystyle e}$, ${\displaystyle f}$ ${\displaystytle v,e,f}$는 씨앗의 정점, 가장자리, 면(관련)이다$$.y) 및 $v{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$, ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$, ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$은(는) 결과의 정점, 가장자리 및 면이다.

${\displaystyle {\mathbf{M}}_{}}$ ${\displaystyle {}_{}}$ [${\displaystyle {}_{}}$v ${\displaystyle \begin{array}{}e\\ \end{array}}$ ${\displaystyle \begin{array}{}f\\ \end{array}}$ ${\displaystyle \begin{array}{}]\end{array}}$=${\displaystyle }$[ ${\displaystyle \begin{array}{c}v{}^{}\end{array}}$ ${\displaystyle \begin{array}{c}{\prime }^{}\end{array}}$ ${\displaystyle \begin{array}{c}e\\ {}^{}\end{array}}$ ${\displaystyle \begin{array}{c}{\prime }^{}\end{array}}$ ${\displaystyle \begin{array}{c}f\\ {}^{}]\end{array}}$ ${\$'\f$'\end{bmatrix$

두 연산자의 구성에 대한 행렬은 두 연산자의 행렬의 곱일 뿐이다.개별 연산자는 예를 들어 p와 l와 같은 행렬을 가질 수 있다.결과의 에지 카운트는 씨앗의 에지 카운트의 정수 배수 d: 이것을 인플레이션율 또는 에지 인자라고 한다.^[7]

가장 단순한 연산자, ID 연산자 S와 이중 연산자 d는 다음과 같은 간단한 행렬 형태를 가지고 있다.

MS)[100010001])나는 3{\displaystyle \mathbf{M}_{S}={\begin{bmatrix}1&, 0&, 0\\0&, 1&, 0\\0&, 0&, 1\end{bmatrix}}=\mathbf{나는}_{3}}, Md){\displaystyle \mathbf{M}_{d}={\begin{bmatrix}0&[001010100], 0&, 1\\0&, 1&, 0\.\1&, 0&, 0\end{bmatrix}}}

dd = S라는 두 개의 이중 연산자가 취소되며, M ${\displaystyle {}_{}}$ ${\$의 제곱이 ID 행렬이다.다른 연산자에 적용할 경우, 이중 연산자는 매트릭스의 수평 및 수직 반사에 해당한다.연산자는 연산자 x, xd(이중 연산자), dx( 연산자 이중), dxd( 연산자 겸용), dxd( 연산자 겸용)를 식별하여 (일부 형식이 동일할 경우) 4개(또는 그 이하)의 그룹으로 분류할 수 있다.이 글에서는 x에 대한 행렬만 주어지는데, 다른 것은 단순한 반사기 때문이다.

연산자수

각 물가상승률의 LSP 수는 물가상승률 1로 시작하는 2,${\displaystyle }$2, $2$, 4,${\displaystyle 6}$,${\displaystyle }$6,${\displaystyle 6}$, ${\displaystyle 20,}$ ${\displaystyle 28,}$ ${\displaystyle 58,}$ 82, ${\displaystyle ,}$ ${\$디스플레이스타일 2,2$,2,4,6,6,20,28,58,82,\cdots }$이다.그러나 모든 LSP가 반드시 3개의 연결 그래프를 형성하는 다면체를 생성하는 것은 아니며, 슈타이니츠의 정리의 결과로서 볼록한 종자로부터 볼록한 다면체를 반드시 생성하는 것은 아니다.각 물가상승률에 대한 3연결 LSP의 수는 $2{\displaystyle \mathrm{}}$,${\displaystyle 2}$,${\displaystyle 4}$,${\displaystyle 6}$,${\displaystyle }$4, ${\displaystyle 20,}$ ${\displaystyle 20,}$ ${\displaystyle 54,}$ ${\displaystyle 64,}$⋯ ${\디스플레이스타일$2$,2,2,4,4,4,20,20,54,64,\cdots }$이다$.$^[8]

원본 작업

엄밀히 말하면, 콘웨이가 시드(S), 니들(n), zip(z)를 포함하지 않았지만, 이중성에 의한 원래의 콘웨이 운영과 관련이 있어 여기에 포함된다.

여기서부터, 수술은 큐브 씨앗에 대해 시각화되어, 큐브 표면에 그려진다.파란 얼굴은 씨앗의 교차 모서리에, 분홍색 얼굴은 씨앗의 꼭지점 위에 놓여 있다.특히 키랄 연산자의 경우 정점의 정확한 위치에는 약간의 유연성이 있다.

오리지널 콘웨이 연산자

에지 계수	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	x	xd	dx	dxd	메모들
1	${\displaystyle {\bmatrix}1&0&0\\0&0&0\\\0&0&1\end{bmatrix}}}$	시드: S	듀얼: d		시드: dd = S	듀얼은 각 정점을 정점으로, 각 정점을 정점으로 대체한다.
2	${\displaystyle {\bmatrix}1&0&1\\0&2&0\\\0&1&0\end{bmatrix}}}$	가입: j		암보: a		조인은 4각형 얼굴을 만든다.Ambo는 도-4 정점을 생성하며, 정류 또는 그래프 이론에서 내적 그래프라고도 한다.[10]
3	${\displaystyle {\bmatrix}1&0&1\\0&3&0\\\0&0&0\end{bmatrix}$	키스:k	바늘: n	Zip: z	잘라내기: t	키스는 각각의 얼굴에 피라미드를 세우고, 아키화, 클라이토프, 응집,[11] 억양 또는 피라미드 증식이라고도 한다.자르는 다면체의 정점을 잘라내지만 원래 가장자리의 일부를 남긴다.[12]Zip은 비트러닝이라고도 불린다.
4	${\displaystyle {\bmatrix}1&1\0&1\0&4\\\0&0&0\end{bmatrix}}$	정형외과 : o = jyj		확장: e = aa
5	${\displaystyle {\bmatrix}1&2&1\0&5&0\\0&0&0\end{bmatrix}}$	자이로: g	gd = rgr	sd = rsr	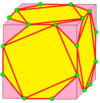스너브: s	치랄 연산자.스너브(지오메트리)를 참조하십시오.Hart와는 반대로 gd는 g: chiral 쌍이다.[3][13]
6	${\displaystyle {\bmatrix}1&1\0&1\0&6&0\\0&4&0\end{bmatrix}}}$	메타: m = kj		베벨: b = ta

씨앗들

어떤 다면체도 그 위에서 작전을 실행할 수 있는 한 씨앗의 역할을 할 수 있다.일반 종자에게 편지가 할당되었다.플라토닉 고형물은 그 이름의 첫 글자(테트라헤드론, 옥타헤드론, 큐브, 이코사헤드론, 도데카헤드론), n-곤의 프리즘(P_n), 항정신병(A_n), 큐폴래(U_n), 항시큐폴레(V_n), 피라미드(Y_n)로 표현된다.존슨 솔리드는 n=1의 경우 J로_n 참조할 수 있다.92.

5개의 플라톤 고형물은 모두 0 ~ 2개의 연산자를 가진 프리즘 발전기에서 생성될 수 있다.^[14]

일반 유클리드 틸링은 또한 씨앗으로 사용될 수 있다.

• Q = 쿼드릴 = 사각 타일링
• H = 헥스티유 = 육각형 타일링 = DΔ
• Δ = 델틸유 = 삼각 타일링 = dH

확장 작업

콘웨이의 원래 세트 이후에 만들어진 작전들이다.이름이 지정된 것보다 더 많은 작업이 존재한다는 점에 유의하십시오. 연산이 여기에 없다고 해서(또는 LSP 또는 LOPSP가 아님) 존재하지 않는 것은 아니다.단순화하기 위해 이 목록에는 수정할 수 없는 연산자만 포함된다. 다른 연산자는 연산자를 함께 구성하여 만들 수 있다.

IMT-2000 3GPP-reducable 확장 연산자

에지 계수	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	x	xd	dx	dxd	메모들
4	${\displaystyle {\bmatrix}1&#2&0\0&4\\\0&1&1\end{bmatrix}}$	챔퍼: c	cd = du	dc = ud	세분화: u	Chamfer는 l의 결합형이다.챔퍼(지오메트리)를 참조하십시오.
5	${\displaystyle {\bmatrix}1&#2&0\0&5\\\0&0&1\end{bmatrix}}$	프로펠러: p	dp = pd		dpd = p	치랄 연산자.프로펠러 조작자는 조지 하트에 의해 개발되었다.[15]
5	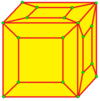${\displaystyle {\bmatrix}1&#2&0\0&5\\\0&0&1\end{bmatrix}}$	로프트: l	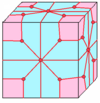ld	dl	굴레를 씌우다
6	${\displaystyle {\bmatrix}1&3&0\0&6\\\0&0&1\end{bmatrix}}$	퀸토: q	qd	dq	dqd.
6	${\displaystyle {\bmatrix}1&#2&0\0&6\\\0&3&1\end{bmatrix}}$	가입 레이스:L0	L0d	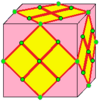dL0	dL0d	조인 표기법에 대한 설명은 아래를 참조하십시오.
7	${\displa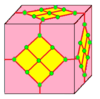ystyle {\bmatrix}1&#2&0\\0&7&0\\\0&4&1\end{bmatrix}}}$	레이스:L	LD	dL	DLD
7	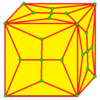${\displaystyle {\bmatrix}1&2&1\0&7&0\\0&4&0\end{bmatrix}}}$	말뚝:K	Kd	dK	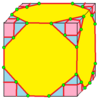dKd
7	${\displaystyle {\bmatrix}1&4&0\\0&7&0\\\0&1\end{bmatrix}}$	회전: w	wd = dv	vd = dw	Volute: v	치랄 연산자.
8	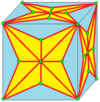${\displaystyle {\bmatrix}1&2&1\0&8&0\\0&0&0\end{bmatrix}}$	${\displaystyle \mathrm{조인-키스-키스}}$:${\displaystyle }$(${\displaystyle {}_{k\mathrm{}}}$ ) 0 ${\$0}}	${\displaystyle (kk)_{0}d}$	${\displaystyle d(kk)_{0}}$	${\displaystyle d(kk)_{0}d}$	때때로 J라는 이름이 붙기도 한다.[4]조인 표기법에 대한 설명은 아래를 참조하십시오.비조인형인 kk는 돌이킬 수 없는 것이 아니다.
10	${\display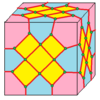style {\bmatrix}1&3&1\\0&10&0\\\0&6&0\end{bmatrix}}}$	X 십자형	엑스드	dX	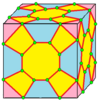dXd

인덱싱된 확장 작업

일부 기준에 따라 여러 연산자를 그룹화하거나 인덱스에 의해 동작이 수정될 수 있다.^[4]이들은_n x라는 첨자로 연산자로 기록된다.

확대

증강 작업은 원래 가장자리를 유지한다.그것들은 면의 어떤 독립적인 부분집합에 적용될 수도 있고, 원래의 가장자리를 제거하여 결합 형태로 변환될 수도 있다.콘웨이 표기법은 이러한 연산자에 대한 선택적 지수를 지원한다. 즉, 결합 양식의 경우 0 또는 영향을 받는 면이 몇 개인지의 경우 3 이상이다.예를 들어, kY₄₄=O: 정사각형 기반 피라미드를 취하고 다른 피라미드를 정사각형 베이스에 붙이면 8각형이 된다.

연산자	k	l	L	K	(kk)
x
x0	k0 = j	l0 = c	L0	K0 = jk	${\displaystyle (kk)_{0}}$
확대	피라미드	프리즘	항정신병

절단 연산자 t에도 지수 형식이 있으며_n, 이는 특정도의 정점만 잘린다는 것을 나타낸다.그것은 dkd에_n 해당한다.

확장 연산자 중 일부는 k_n, t_n 연산자와 함께 특수한 경우에 만들어질 수 있다.예를 들어 모따기 큐브인 cC는 tdaC₄, rhombic do데카헤드론, daC 또는 jC로 구성될 수 있으며, 도-4 정점이 잘려 있다.로프트 큐브인 lc는 tkc와₄ 같다.5진법 qD는 tdaaD₅, tdeD₅ 또는 todD₅, toD로 구성될 수 있으며, 도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-도-

메타/비벨

메타는 가운데와 가장자리를 따라 정점을, 베벨은 가운데, 시드 정점, 가장자리를 따라 정점을 추가한다.지수는 가장자리를 따라 정점 또는 면의 수를 더한 것이다.메타(비인덱스 형태)는 캔트런지(cantitruncation) 또는 옴니트런지(hunitruncation)라고도 한다.여기서 0은 확대 연산과 같은 것을 의미하지 않는다는 점에 유의하십시오. 즉, 가장자리를 따라 정점(또는 면)이 0으로 추가된다는 것을 의미한다.^[4]

메타/비벨 연산자

n	에지 계수	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	x	xd	dx	dxd
0	3	${\displaystyle {\bmatrix}1&0&1\\0&3&0\\\0&0&0\end{bmatrix}$	k = m0	n	z = b0	t
1	6	${\displaystyle {\bmatrix}1&1\0&1\0&6&0\\0&4&0\end{bmatrix}}}$	m = m1 = kj		b = b1 = ta
2	9	${\di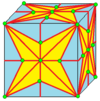splaystyle {\bmatrix}1&2&1\0&9&0\\0&6&0\end{bmatrix}}}$	m2	m2d	b2	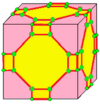b2d
3	12	${\displaystyle {\bmatrix}1&3&1\\0&12&0\\\0&8&0\end{bmatrix}}}$	m3	m3d	b3	b3d
n	3n+3	${\displaystyle {\bmatrix}1&n&1\\0&3n+3n+3&0\0&n+2&0\end{bmatrix}}}$	mn	mnd	bn	bnd

메디알

중심에서 각 시드 정점에 가장자리를 추가하지 않는다는 점을 제외하면 메디알은 메타와 같다.지수 1 형태는 콘웨이의 정형외과와 확장 연산자와 동일하다. 확장(expansion)은 확장과 확장(cantellation)이라고도 한다.o와 e는 아래에 설명된 자체 인덱싱된 양식을 가지고 있다는 점에 유의하십시오.또한 일부 구현에서는 1이 아닌 0에서 인덱싱을 시작한다는 점에 유의하십시오.^[4]

중간 연산자

n	가장자리 요소	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	x	xd	dx	dxd
1	4	${\displaystyle {\bmatrix}1&1\0&1\0&4\\\0&0&0\end{bmatrix}}$	M1 = o = jyj		e = aa
2	7	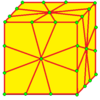${\displaystyle {\bmatrix}1&2&1\0&7&0\\0&4&0\end{bmatrix}}}$	중위수: M = M2	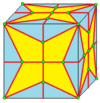md	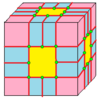dM	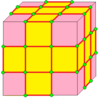dMd
n	3n+1	${\displaystyle {\bmatrix}1&n&1\\0&3n+1&0\0&n&0\end{bmatrix}}}$	Mn	mdn	dMn	dMnd

골드버그콕시터

골드버그-콕세터(GC) 콘웨이 운영자는 골드버그-콕세터 건설의 연장선인 두 무한 연산자 계열이다.^[16][17]GC 구조는 삼각 격자의 삼각형 부분 또는 사각 격자의 사각형 부분을 취하여 다면체의 각 면 위에 놓는 것으로 생각할 수 있다.이 구조는 삼각형이나 사각형의 챔버("마스터 폴리곤")를 식별하여 어떤 면으로도 확장할 수 있다.^[7]삼각형 계열의 연산자는 Goldberg Polyedra와 Geodesic Polyedra를 생산하는 데 사용될 수 있다: 공식은 Geodesic Polyedra와 Goldberg Polyedra 목록을 참조한다.

두 가문은 삼각형 GC 계열, c와_a,b u_a,b, 그리고 4각형 GC 계열, e와_a,b o이다_a,b.두 GC 제품군은 모두${\displaystyle \mathrm{two}}$ 1 ${\displaystyle a\geq$1}과 b${\displaystyle 0}$ 0$${\$displaystyle b\geq$0}의 두 정수로 지수화된다$.$그들은 많은 훌륭한 자질들을 가지고 있다.

• 그 가족의 지수는 복잡한 숫자에 걸쳐 특정한 유클리드 영역과 관계를 가진다: 삼각형 GC 계열의 아이젠슈타인 정수와 4각형 GC 계열의 가우스 정수.
• 같은 가족 내 xxd기둥과 dxd기둥의 운영자들이 서로 통근한다.

운영자는 3가지 등급으로 구분된다(예는 c로 작성되지만 4개 운영자 모두에게 적용).

• 클래스 I: $b{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle b=0$ 아키랄, 원래 가장자리를 보존한다.0 지수를 억제한 상태로 작성할 수 있다(예_a,0: c = c_a).
• $클래스{\displaystyle }$ II: ${\displaystyle a}$= b ${\displaystyle a=b}$. 또한 아치랄.c_a,a = cc로_a1,1 분해할 수 있음
• 클래스 III: 다른 모든 연산자.이것들은 치랄이고, c와_a,b c는_b,a 서로 치랄 쌍이다.

원래 콘웨이 작전 중 GC 계열에 속하지 않는 것은 g와 s(자이로와 스너브)뿐이다.메타(meta)와 베벨(m과 b)은 삼각형 계열의 연산자 1명과 사각형 계열의 연산자 1명으로 표현할 수 있다.

삼각형

삼각 골드버그-콕시터 연산자

a	b	클래스	에지 계수 T = a2 + ab + b2	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	마스터 삼각형	x	xd	dx	dxd
1	0	I	1	${\displaystyle {\bmatrix}1&0&0\\0&0&0\\\0&0&1\end{bmatrix}}}$		u1 = S	d		c1 = S
2	0	I	4	${\displaystyle {\bmatrix}1&#1&0\0&0&0\\\0&1\end{bmatrix}}$		u2 = u	dc	du	c2 = c
3	0	I	9	${\displaystyle {\bmatrix}1&2&1\0&9&0\\0&6&0\end{bmatrix}}}$		u3 = nn	nk	zt	c3 = zz
4	0	I	16	${\displaystyle {\bmatrix}1&5&0\\0&16&0\\\0&10&1\end{bmatrix}}}$		u4 = uu	ud = dcc	duuu = ccd	c4 = cc
5	0	I	25	${\displaystyle {\bmatrix}1&#8&0\\0&25&0\\\0&16&1\end{bmatrix}}}$		u5	u5d = dc5	du5 = c5d	c5
6	0	I	36	${\displaystyle {\bmatrix}1&11&1\\0&360\\0&24&0\end{bmatrix}}}$		u6 = unn	풀다	czt	u6 = czz
7	0	I	49	${\displaystyle {\bmatrix}1&16&0\0&49&0\\\0&32&1\end{bmatrix}}}$		u7 = u2,1u1,2 = vrv	vrvd = dwrw.	dvrv = wrwd	c7 = c2,1c1,2 = wrw
8	0	I	64	${\displaystyle {\bmatrix}1&21&0\\0&64&0\\\0&42&1\end{bmatrix}}}$		u8 = u3	u3d = dc3	du3 = c3d	c8 = c3
9	0	I	81	${\displaystyle {\bmatrix}1&26&1\\0&81&0\\\0&54&0\end{bmatrix}}}$		u9 = n4	n3k = kz3	tn3 = z3t	c9 = z4
1	1	II	3	${\displaystyle {\bmatrix}1&0&1\\0&3&0\\\0&0&0\end{bmatrix}$		u1,1 = n	k	t	c1,1 = z
2	1	III	7	${\displaystyle {\bmatrix}1&#2&0\\0&7&0\\\0&4&1\end{bmatrix}}}$		v = u2,1	vd = dw	dv = wd	w = c2,1
3	1	III	13	${\displaystyle {\bmatrix}1&4&0\0&13&0\\\0&8&1\end{bmatrix}}}$		u3,1	u3,1d = dc3,1	du3,1 = c3,1d	c3,1
3	2	III	19	${\displaystyle {\bmatrix}1&6&0\0&190\\\0&12&1\end{bmatrix}}$		u3,2	u3,2d = dc3,2	du3,2 = c3,2d	c3,2
4	3	III	37	${\displaystyle {\bmatrix}1&12&0\\0&37&0\\\0&24&1\end{bmatrix}}}$		u4,3	u4,3d = dc4,3	du4,3 = c4,3d	c4,3
5	4	III	61	${\displaystyle {\bmatrix}1&20&0\\0&61&0\\\0&40&1\end{bmatrix}}}$		u5,4	u5,4d = dc5,4	du5,4 = c5,4d	c5,4
6	5	III	91	${\displaystyle {\bmatrix}1&30&0\\0&91&0\\\0&60&1\end{bmatrix}}}$		u6,5 = u1,2u1,3	u6,5d = dc6,5	du6,5 = c6,5d	c6,5=c1,2c1,3
7	6	III	127	${\displaystyle {\bmatrix}1&42&0\0&#0&#0&#0\\0&84&1\end{bmatrix}}$		u7,6	u7,6d = dc7,6	du7,6 = c7,6d	c7,6
8	7	III	169	${\displaystyle {\bmatrix}1&56&0\0&#0&#0\\0&#1\end{bmatrix}}$		u8,7 = u3,12	u8,7d = dc8,7	du8,7 = c8,7d	c8,7 = c3,12
9	8	III	217	${\displaystyle {\bmatrix}1&72&0\0&217&0\\\0&#1\end{bmatrix}}$		u9,8 = u2,1u5,1	u9,8d = dc9,8	du9,8 = c9,8d	c9,8 = c2,1c5,1
$a\equiv b}$${\displaystyle \(\mathrm {mod} \ 3)}$		I, II 또는 III	$T\equiv 0\ }$${\displaystyle(\mathrm {mod} \ 3)}$	${\displaystyle {\begin{bmatrix}1>{\frac {T}{3}-1\\0>T&0\\0&{\frac {2}{3}T&0\end{bmatrix}}$	...	ua,b	ua,bd = dca,b	dua,b = ca,bd	ca,b
$\\displaystyle a\not \equiv b}$${\displaystyle \(\mathrm {mod} \ 3)}$		I 또는 III	$T\displaystyle T\equiv 1}$${\displaystyle \(\mathrm {mod} \ 3)}$	${\displaystyle {\begin{bmatrix}1&#{\frac {T-1}{3}&#0\0&#•T&0\\0&2{\frac {T-1}{3}&1\end{bmatrix}}}$	...	ua,b	ua,bd = dca,b	dua,b = ca,bd	ca,b

기본 숫자 이론에 따르면 $a$와 b의 모든 ${\displaystyle \mathrm{값}}$에 대해 T ${\displaystyle \not\equiv }$ 2 ${\displaystyle \text{(}m\mathrm{}}$ ${\displaystyle \mathrm{o}}$ d ${\displaystyle 3\mathrm{}}$) ${\displaystyle T\not \equiv 2\ (\mathrm$ {$mod} \ 3$

4각형

사각 골드버그-콕시터 연산자

a	b	클래스	에지 계수 T = a2 + b2	매트릭스 $M{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$	마스터 스퀘어	x	xd	dx	dxd
1	0	I	1	${\displaystyle {\bmatrix}1&0&0\\0&0&0\\\0&0&1\end{bmatrix}}}$		o1 = S	e1 = d		o1 = dd = S
2	0	I	4	${\displaystyle {\bmatrix}1&1\0&1\0&4\\\0&0&0\end{bmatrix}}$		o2 = o = j2		e2 = e = a2
3	0	I	9	${\displaystyle {\bmatrix}1&4&0\0&9&0\\\0&1\nd{bmatrix}}$		o3	e3		o3
4	0	I	16	${\displaystyle {\bmatrix}1&7&1\0&16&0\\0&8&0\end{bmatrix}}}$		o4 = oo = j4		e4 = ee = a4
5	0	I	25	${\displaystyle {\bmatrix}1&12&0\\0&25&0\\\0&12&1\end{bmatrix}}}$		o5 = o2,1o1,2 = prp	e5 = e2,1e1,2		o5= dprpd
6	0	I	36	${\displaystyle {\bmatrix}1&17&1\\0&360\\0&18&0\end{bmatrix}}}$		o6 = o2o3		e6 = e2e3
7	0	I	49	${\displaystyle {\bmatrix}1&24&0\\0&49&0\\\0&24&1\end{bmatrix}}}$		o7	e7		o7
8	0	I	64	${\displaystyle {\bmatrix}1&31&1\\0&64&0\\\0&32&0\end{bmatrix}}}$		o8 = o3 = j6		e8 = e3 = a6
9	0	I	81	${\displaystyle {\bmatrix}1&40&0\\0&81&0\\\0&40&1\end{bmatrix}}}$		o9 = o32	e9 = e32		o9
10	0	I	100	${\displaystyle {\bmatrix}1&49&1\\0&100&0\\\0&50&0\end{bmatrix}}}$		o10 = OOO2,11,2		e10 = ee2,1e1,2
1	1	II	2	${\displaystyle {\bmatrix}1&0&1\\0&2&0\\\0&1&0\end{bmatrix}}}$		o1,1 = j		e1,1 = a
2	2	II	8	${\displaystyle {\bmatrix}1&3&1\0&8&0\\0&4&0\end{bmatrix}}}$		o2,2 = j3		e2,2 = a3
1	2	III	5	${\displaystyle {\bmatrix}1&#2&0\0&5\\\0&0&1\end{bmatrix}}$		o1,2 = p	e1,2 = dp = pd		p
$a\equiv b}$${\displaystyle \(\mathrm {mod} \ 2)}$		I, II 또는 III	T 짝수	${\displaystyle {\begin{bmatrix}1&{\frac {T}{2}}-1\\0>T&0\\0&{\frac {T}{2}}&0\end{bmatrix}}}$	...	oa,b		ea,b
$\\displaystyle a\not \equiv b}$${\displaystyle \(\mathrm {mod} \ 2)}$		I 또는 III	T 홀수	${\displaystyle {\begin{bmatrix}1&#{\frac {T-1}{2}}&#0\0&#•T&0\\0&{\frac {T-1}{2}}&1\end{bmatrix}}$	...	oa,b	ea,b		oa,b

예

지질 다면체 및 골드버그 다면체 목록도 참조하십시오.

아르키메데스 및 카탈루냐 고형분

콘웨이의 원래 연산자 집합은 플라토닉 고형분을 씨앗으로 사용하여 아르키메데스 고형물과 카탈루냐 고형분을 모두 만들 수 있다. (r 연산자는 두 가지 키랄 형태를 모두 만들 필요가 없다는 점에 유의한다.)

• 아르키메데스
• 

  잘린 사면체
  tT

• 

  큐폭타헤드론
  aC = aaT

• 

  잘린 큐브
  tC

• 

  잘린 팔면체
  tO = bT

• 

  롬비큐옥타헤드론
  eC = a³T

• 

  잘린 칸옥타헤드론
  bC

• 

  정육면체를 잘라내다
  sc

• 

  이코시다데카헤드론
  AD

• 

  잘린 도두면체
  tD

• 

  잘린 이두면체
  TI

• 

  롬비코시도데카헤드론
  eD

• 

  잘린 이코시다데카헤드론
  bD

• 

  달팽이관
  sD&sI

• 카탈루냐 주
• 

  삼면체
  kT

• 

  롬빅 도데카헤드론
  jC

• 

  삼면체
  kO

• 

  테트라키스 육면체
  kC

• 

  델토이탈 이코시테트라헤드론
  oc

• 

  디디아키스 도데카헤드론
  mC

• 

  오각형 이코시테트라헤드론
  gC

• 

  롬빅 삼권면체
  jd

• 

  트리아키스 이코사면체
  KI

• 

  펜타키스 도데카헤드론
  kD

• 

  델토이탈 육면체
  oD

• 

  디디아키스 삼권면체
  md

• 

  오각형 육면체
  gD&gI

복합 연산자

잘린 이코사면체 tI = zD는 씨앗으로 사용되어 정점이나 얼굴 변환은 아니지만, 좀 더 시각적으로 쾌적한 다면체를 만들 수 있다.

• 

  tI=zD

• 

  앳아이

• 

  ttI

• 

  ztI

• 

  etI

• 

  BTI

• 

  StI

• 듀얼스
• 

  nI=kD

• 

  jtI

• 

  ntI

• 

  ktI

• 

  OTI

• 

  mtI

• 

  GTI

그 비행기에.

볼록한 각 균일 기울기는 콘웨이 연산자를 일반 기울기 Q, H, Δ에 적용하여 만들 수 있다.

• 

  사각 타일링
  Q=dQ

• 

  잘린 사각 타일링
  tQ

• 

  테트라키스 네모난 타일
  kQ

• 

  스너브 사각 타일링
  sQ

• 

  카이로 오각형 타일링
  gQ

• 

  육각 타일링
  H = Δ

• 

  삼헥사각 타일링
  aH = Δ

• 

  잘린 육각 타일링
  tH

• 

  Rhombitrihexangle tiling
  eH = Δ

• 

  잘린 3hexangel 타일링
  bH = BΔ

• 

  스너브삼각형 타일링
  sH = Δ

• 

  삼각 타일링
  Δ = dH

• 

  롬빌 타일링
  Δ = jH

• 

  트리아키스 삼각 타일링
  Δ

• 

  삼각 타일링
  Δ = oH

• 

  키스롬빌 타일링
  Δ = mH

• 

  플레어트 오각형 타일링
  Δ = gH

토러스에서

콘웨이 연산자는 여러 개의 구멍이 있는 토로이드성 다면체 및 다면체에도 적용할 수 있다.

• 

  1x1 일반 사각형 토러스, {4,4}_1,0

• 

  일반 4x4 제곱 토러스, {4,4}_4,0

• 

  tQ24×12가 torus에 투영됨

• 

  taQ24×12가 torus에 투영됨

• 

  actQ24×8이 torus에 투영됨

• 

  tH24×12가 torus에 투영됨

• 

  taH24×8이 torus에 투영됨

• 

  kH24×12가 torus에 투영됨

참고 항목

위키미디어 커먼즈에는 콘웨이 폴리헤드라 관련 미디어가 있다.

• 대칭면체
• 조노헤드론
• 슐레플리 기호

참조

외부 링크

• polyHégapisme: HTML5 캔버스에서 폴리헤드라를 생성하여 Conway 표기법을 입력으로 사용