그래프역학계

수학에서, 그래프 동적 시스템의 개념은 그래프나 네트워크에서 일어나는 광범위한 과정을 포착하는 데 사용될 수 있다.GDS의 수학적 및 계산적 분석에서 주요 주제는 구조 특성(예: 네트워크 연결성)과 그로 인해 발생하는 글로벌 역학을 연관시키는 것이다.

GDS에 대한 연구는 유한 그래프와 유한 상태 공간을 고려한다.이와 같이, 연구에는 일반적으로 차등 기하학보다는 그래프 이론, 조합론, 대수학, 동력학 등의 기법이 포함된다.원칙적으로 무한 그래프( $\mathbb {Z} ^{k}$ : Z $\mathbb {Z} ^{k}$ ${\$ ^{k $})$ 를 ${\mathb{Z}^{k}$ 통한 GDS와 무한 상태 공간(예: $\mathbb {R}$ {\ $displaystyle \mathb {R}})$ 을 $\mathb {R}$ 통한 GDS를 정의하고 연구할 수 있다.플레드 맵 래티스), 예를 들어 우를 참조하십시오.^[1]다음에서, 모든 것은 달리 명시되지 않는 한 암묵적으로 유한하다고 가정한다.

형식 정의

그래프 동적 시스템은 다음 구성 요소로 구성된다.

정점 집합 v[Y] = {1,2, ..., n}인 유한 그래프 Y.상황에 따라 그래프를 지시하거나 방향을 바꿀 수 있다.

유한 집합 K에서 가져온 Y의 각 꼭지점 v에 대한 상태_v x시스템 상태는 n-투플 x = (x₁₂, x, ... , x_n)이고, x[v]는 Y에서 v의 1-근접점(일부 고정된 순서)에 있는 정점과 관련된 상태로 구성된 튜플이다.

각 꼭지점 v에 대한 꼭지점 함수_v f.정점 함수는 Y에서 v의 1-근접과 관련된 상태를 기준으로 시간 t + 1의 정점 상태에 시간 t의 정점 v의 상태를 매핑한다.

개별 꼭지점 상태의ⁿ 매핑이ⁿ 수행되는 메커니즘을 명시하여 지도 F: K → K를 가진 이산 동적 시스템을 유도한다.

지도 F: Kⁿ → K가ⁿ 있는 동적 시스템과 연관된 위상 공간은 정점 집합 K와ⁿ 방향 에지(x, F(x))가 있는 유한 방향 그래프다.위상 공간의 구조는 그래프 Y, 정점 함수(f_i) _i및 업데이트 스키마의 속성에 의해 제어된다.이 분야의 연구는 시스템 구성 요소의 구조에 기초하여 위상 공간 특성을 유추하고자 한다.그 분석은 지역 대 지구적 성격을 가지고 있다.

일반 셀룰러 오토마타(GCA)

예를 들어, 업데이트 체계가 정점 함수를 동시에 적용하는 것으로 구성되면 일반화된 세포 자동 분류(CA)를 얻는다.이 경우 글로벌 맵 F: Kⁿ → K에ⁿ 의해 주어진다.

$F(x)_{v}=f_{v}(x[v])\;$

고전적 또는 표준적 세포 자동자산은 일반적으로 일반 그래프나 그리드에 걸쳐 정의되고 연구되며, 정점 함수는 일반적으로 동일하다고 가정하기 때문에 이 세분류를 일반화된 세포 자동자라 칭한다.

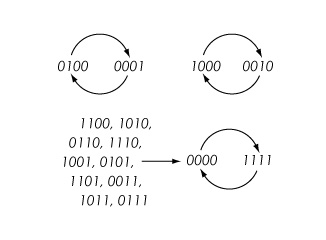
예: 가장자리가 {1,2}, {2,3}, {3,4}, {1,4}, {1,4}, {1,4}인 꼭지점 {1,2,3,4}에 있는₄ 원 그래프가 되도록 한다.K = {0,1}을(를) 각 꼭지점의 상태 공간으로 하고 함수 nor₃ : nor₃(x,y,z)로 정의한 K³ → K = (1 + x)(1 + y)(1 + z)로 모든 꼭지점 함수에 대한 산술모듈로 2를 사용하여 함수를 사용한다.그런 다음 시스템 상태(0,1,0,0)는 동기 업데이트를 사용하여 (0,0,0,0,1)로 매핑된다.모든 전환은 아래 위상 공간에 표시된다.

326

순차 동적 시스템(SDS)

If the vertex functions are applied asynchronously in the sequence specified by a word w = (w₁, w₂, ... , w_m) or permutation $\pi$ = ( $\pi _{1}$ , $\pi _{2},\dots ,\pi _{n}$ ) of v[Y] one obtains the class of Sequential dynamical systems (SDS).^[2]이 경우, 다음과 같은 방법으로 정점함수로 구성된 Y-로컬 맵 F를_i 도입하는 것이 편리하다.

F_{i}(x)=(x_{1},x_{2},\ldots,x_{i-1},f_{i}(x[i]),x_{i+1},\ldots,x_{n}\;

SDS 지도 F = [F_Y , w] : K → K는ⁿ 함수ⁿ 구성이다.

[F_{Y},w]=F_{w(m)}\circ F_{w(m-1)}\circdots \circ F_{w(2)\circdots \circdots \circus F_{w(1)}.

업데이트 순서가 순열인 경우, 이 점을 강조하기 위해 순열 SDS를 자주 언급한다.

예: 가장자리가 {1,2}, {2,3}, {3,4}, {1,4}, {1,4}, {1,4}인 꼭지점 {1,2,3,4}에 있는₄ 원 그래프가 되도록 한다.K={0,1}를 각 꼭지점의 상태 공간으로 하고, nor₃(x, y, z)로 정의한 K³ → K = (1 + x)(1 + y)(1 + y)(1 + z)로 모든 꼭지점 함수에 대해 산술모듈로 2를 사용하여 함수를 사용한다₃.업데이트 순서(1,2,3,4)를 사용하여 시스템 상태(0, 1, 0, 0)를 (0, 0, 1, 0)로 매핑한다.이 순차적 동적 시스템에 대한 모든 시스템 상태 전환은 아래 위상 공간에 표시된다.

326

확률적 그래프 역학 시스템

예를 들어, 애플리케이션의 관점에서 보면 GDS의 구성 요소 중 하나 이상이 확률적 요소를 포함하는 경우를 고려하는 것이 흥미롭다.동기부여 애플리케이션에는 완전히 이해되지 않은 프로세스(예: 세포 내의 역학)와 모든 실제 목적을 위한 특정 측면이 어떤 확률 분포에 따라 작용하는 것처럼 보이는 프로세스가 포함될 수 있다.또한 확률론적 근사를 고려하는 것이 타당할 정도로 설명이 복잡하거나 다루기 어려운 결정론적 원리에 의해 지배되는 응용 프로그램도 있다.

그래프 동적 시스템의 모든 요소는 여러 가지 방법으로 확률적으로 만들어질 수 있다.예를 들어 순차적 동적 시스템에서 업데이트 시퀀스는 확률적으로 만들어질 수 있다.각 반복 단계에서 해당 확률을 가진 업데이트 시퀀스의 주어진 분포에서 무작위로 w 업데이트 시퀀스를 선택할 수 있다.업데이트 시퀀스의 일치 확률 공간은 SDS 맵의 확률 공간을 유도한다.이와 관련하여 연구해야 할 자연적인 물체는 이 SDS 맵 컬렉션에 의해 유도된 상태 공간의 마르코프 체인이 있다.이 경우를 업데이트 시퀀스 확률적 GDS라고 하며, 예를 들어 특정 비율(예: 화학 반응), 병렬 계산/분산 이벤트 시뮬레이션에서의 동기화 및 나중에 설명된 계산 패러다임에서 "이벤트"가 무작위로 발생하는 프로세스에서 동기를 부여한다.

확률적 업데이트 순서의 이 특정 사례는 그러한 시스템에 대한 두 가지 일반적인 사실을 보여준다: 확률적 그래프 동적 시스템으로 전달될 때 일반적으로 (1) 마코프 체인에 대한 연구(GDS의 구성요소에 의해 관리되는 특정 구조 포함)와 (2) 결과 마코프 체인은 지수 n을 갖는 큰 경향이 있다.여러 나라확률론적 GDS 연구의 중심 목표는 축소된 모델을 도출할 수 있는 것이다.

정점 기능이 확률적인 경우, 즉 기능 확률적 GDS도 고려할 수 있다. 예를 들어, 무작위 부울 네트워크는 동기식 업데이트 체계를 사용하는 기능 확률적 GDS의 예로서 상태 공간이 K = {0, 1}인 경우를 들 수 있다.유한확률론적 세포자동화(PCA)는 기능 확률론적 GDS의 또 다른 예다. 원칙적으로 인터랙티브 입자 시스템(IPS)의 등급은 유한하고 무한한 PCA를 다루지만, 실제로 IPS에 관한 작업은 상태공간에 더 흥미로운 토폴로지를 도입할 수 있게 해주기 때문에 무한 사례에 크게 관련된다.

적용들

그래프 동적 시스템은 생물학적 네트워크나 전염병 같은 분산 시스템을 소셜 네트워크를 통해 포착하기 위한 자연적인 프레임워크를 구성하는데, 이 중 많은 시스템을 복잡한 시스템이라고 자주 언급한다.

참고 항목

참조

^ Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.
^ Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

추가 읽기

Macauley, Matthew; Mortveit, Henning S. (2009). "Cycle equivalence of graph dynamical systems". Nonlinearity. 22 (2): 421–436. arXiv:0802.4412. Bibcode:2009Nonli..22..421M. doi:10.1088/0951-7715/22/2/010.
Golubitsky, Martin; Stewart, Ian (2003). The Symmetry Perspective. Basel: Birkhauser. ISBN 0-8176-2171-7.

외부 링크

그래프 동적 시스템 – 헤닝 모르트베이트에 의한 상호작용 기반 시스템, 분석 및 시뮬레이션에 대한 수학 프레임워크

[wu-05-1] Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.

[Mortveit-08-2] Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

[1]

[2]

Search