해밍(7,4)

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "해밍(7,4) – 뉴스 · 신문 · 책 · 학자 · JSTOR(2019년 6월) (이 템플릿 메시지 삭제 방법과 시기 학습)

해밍(7,4)-코드
이름을 따서 명명됨	리처드 해밍
분류
유형	선형블록코드
블록 길이	7
메시지 길이	4
등급	4/7 ~ 0.571
거리	3
알파벳 크기	2
표기법	[7,4,3]-2코드
특성.
완벽한 암호
v t

코딩 이론에서 해밍(7,4)은 3개의 패리티 비트를 추가하여 4개의 데이터 비트를 7비트로 인코딩하는 선형 오류 수정 코드다. 해밍 코드의 대가족 구성원이지만 해밍 코드라는 용어는 리차드 W. 해밍이 1950년에 도입한 이 특정 코드를 가리키는 경우가 많다. 당시 해밍은 벨 전화 연구소에서 일하다가 오류가 발생하기 쉬운 펀치 카드 리더기에 좌절해 오류 수정 코드 작업에 착수했다.^[1]

해밍 코드는 메시지의 4개 데이터 비트마다 3개의 체크 비트를 추가한다. 해밍의 (7,4) 알고리즘은 모든 단일 비트 오류를 수정하거나, 모든 단일 비트 및 2비트 오류를 감지할 수 있다. 즉, 어떤 두 개의 정확한 암호어 사이의 최소 해밍 거리는 3이며, 수신된 단어가 송신자가 전송한 암호어로부터 최대 1개의 거리에 있으면 정확하게 해독할 수 있다. 이는 버스트 에러가 발생하지 않는 전송 매체 상황의 경우 해밍(7,4) 코드가 유효하다는 것을 의미한다(매체는 7비트 중 2비트를 플립하려면 극도로 시끄러워야 하기 때문이다).

양자정보에서 해밍(7,4)은 양자오류보정에 사용되는 CSS 코드의 일종인 스테인 코드의 베이스로 사용된다.

목표

해밍 코드의 목표는 데이터 비트나 패리티 비트의 단일 비트 오류를 감지하고 수정할 수 있도록 겹치는 패리티 비트 세트를 생성하는 것이다. 중복이 여러 개 생성될 수 있지만 일반적인 방법은 해밍 코드로 제시된다.

비트 #	1	2	3	4	5	6	7
전송 비트	${\displaystyle p_{1}.$	${\displaystyle p_{2}}:$	${\displaystyle d_{1}.$	${\displaystyle p_{3}}$	${\displaystyle d_{2}}:$	${\displaystyle d_{3}}$	${\displaystyle d_{4}}$
${\displaystyle p_{1}.$	네	아니요.	네	아니요.	네	아니요.	네
${\displaystyle p_{2}}:$	아니요.	네	네	아니요.	아니요.	네	네
${\displaystyle p_{3}}$	아니요.	아니요.	아니요.	네	네	네	네

이 표는 인코딩된 워드에서 전송된 비트를 포함하는 패리티 비트를 설명한다. 예를 들어, p는₂ 비트 2, 3, 6, 7에 균등 패리티를 제공한다. 칼럼을 읽어 어떤 전송 비트가 어떤 패리티 비트로 커버되는지 상세하게 기술한다. 예를 들어, d는₁₁ p와₂ p로 다루어지지만 p는₃ 아니다. 이 표는 다음 절의 패리티-체크 매트릭스(H)와 현저하게 유사하다.

또한 위 표의 패리티 열이 제거된 경우

	${\displaystyle d_{1}.$	${\displaystyle d_{2}}:$	${\displaystyle d_{3}}$	${\displaystyle d_{4}}$
${\displaystyle p_{1}.$	네	네	아니요.	네
${\displaystyle p_{2}}:$	네	아니요.	네	네
${\displaystyle p_{3}}$	아니요.	네	네	네

그러면 아래의 코드 생성기 매트릭스(G)의 1, 2, 4행과 유사한 점이 또한 명백해질 것이다.

따라서 패리티 비트 커버리지를 정확하게 선택하면 해밍 거리 1의 모든 오류를 감지하여 수정할 수 있는데, 해밍 코드를 사용하는 포인트다.

해밍 행렬

해밍 코드는 선형 코드이기 때문에 행렬을 통해 선형 대수 용어로 계산할 수 있다. 해밍 코드의 목적상, 코드 생성기 매트릭스 G와 패리티 체크 매트릭스 H:

${\displaystyle \mathbf {G^{T}}:={\begin{pmatrix}1&, 1&, 0&, 1\\1&, 0&, 1&, 1\\1&, 0&, 0&, 0\\0&, 1&, 1&, 1\\0&, 1&, 0&, 0\\0&, 0&, 1&, 0\\0&, 0&, 0&, 1\\\end{pmatrix}},\qquad\mathbf{H}:={\begin{pmatrix}1&, 0&, 1&, 0&, 1&, 0&, 1\\0&, 1&, 1&, 0&, 0&, 1&, 1\\0&, 0&, 0&, 1&, 1&, 1&, 1\\\end{pmatrix.}}.}$

위에서 언급한 바와 같이 G의 1, 2, 4행은 데이터 비트를 패리티 비트에 매핑할 때 친숙하게 보여야 한다.

• p₁₄ 커버 d, d₁, d₂
• p₂₄ 커버 d, d₁, d₃
• p₃₄ 커버 d, d₂, d₃

나머지 행(3, 5, 6, 7)은 데이터를 인코딩된 형태로 자신의 위치에 매핑하고 해당 행에는 1개만 있으므로 동일한 복사본이다. 사실 이 네 개의 행은 선형적으로 독립적이며 (우연이 아닌 설계에 의해) 아이덴티티 행렬을 형성한다.

또한 위에서 언급한 바와 같이 H의 3열은 친숙해야 한다. 이러한 행은 수신 엔드에서 신드롬 벡터를 계산하는데 사용되며, 신드롬 벡터가 null 벡터(모든 0)인 경우 수신된 단어는 오류가 없으며, 0이 아닌 경우 이 값은 어떤 비트가 플립되었는지 나타낸다.

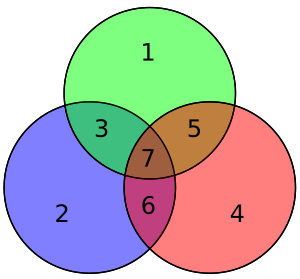
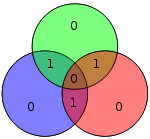
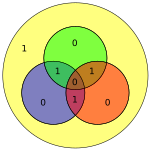
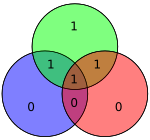
벡터 p로 조립된 4개의 데이터 비트는 Gp(즉, Gp)에 의해 사전 곱하여 전송되는 인코딩된 값을 산출하기 위해 modulo 2를 취한다. 원본 4개의 데이터 비트는 위의 데이터 비트 커버리지를 사용하여 짝수 패리티를 보장하기 위해 3개의 패리티 비트가 추가된 7비트("Hamming(7,4)"로 변환된다. 위의 첫 번째 표는 각 데이터와 패리티 비트를 최종 비트 위치(1 ~ 7)로 매핑하는 것을 보여주지만, 이는 Venn 다이어그램으로도 표시할 수 있다. 이 글의 첫 번째 다이어그램은 세 개의 원(패리티 비트당 하나씩)을 보여주고 각 패리티 비트가 포함하는 데이터 비트를 포함한다. 두 번째 다이어그램(오른쪽 표시)은 동일하지만, 대신 비트 위치가 표시된다.

이 섹션의 나머지 부분에서는 다음과 같은 4비트(칼럼 벡터로 표시)를 실행 예제로 사용한다.

${\displaystyle \mathbf {p} ={\pmatrix}d_{1}\\d_\d}\d_{4}\\end{pmatrix}={\pmatrix}1\0\\\1\end{pmatrix}}}={pmatrix}}}}}}}}}}}}$

채널 코딩

이 데이터를 전송한다고 가정합시다.1011 ( ) 시끄러운 통신 채널을 통해. 특히 오류 손상이 0이나 1을 선호하지 않는다는 뜻의 2진수 대칭 채널(오류를 발생시키는 경우 대칭)은 0이나 1을 선호하지 않는다. 또한 모든 소스 벡터는 장착 가능한 것으로 가정한다. 우리는 전송된 코드 워드 x를 결정하기 위해 G와 p의 제품을 modulo 2와 함께 가져간다.

${\displaystyle \mathbf {x} =\mathbf {G^{T}} \mathbf {p} ={\begin{pmatrix}1&1&0&1\\1&0&1&1\\1&0&0&0\\0&1&1&1\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\3\\1\\2\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}}$

라는 뜻이다. 0110011 전송하는 대신에 전송될 것이다. 1011.

곱셈을 염려하는 프로그래머는 결과의 각 행이 곱하기보다는 행과 컬럼이 비트 AND로 합쳐져 생기는 집합 비트의 모집단 카운트 중에서 가장 유의하지 않은 비트임을 관찰해야 한다.

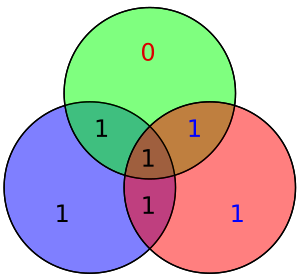
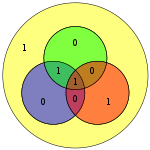
인접한 다이어그램에서 인코딩된 단어의 7비트를 각 위치에 삽입한다. 검사 결과 빨간색, 녹색 및 파란색 원의 비율이 다음과 같은 것이 분명하다.

• 빨간 원은 두 개의 1을 가지고 있다.
• 녹색 원은 두 개의 1을 가지고 있다.
• 파란색 원은 네 개의 1을 가지고 있다.

곧 보여질 것은, 전송 중에 비트를 플립할 경우, 2개 또는 3개 원의 패리티가 모두 부정확하게 되고, 이 세 원 모두의 패리티가 균등해야 한다는 것을 알고서(패리티 비트 중 하나라도) 에러링된 비트를 결정할 수 있다는 것이다.

패리티 조회

전송 중에 오류가 발생하지 않으면 수신된 코드 워드 r은 전송된 코드 워드 x:

${\displaystyle \mathbf {r} =\mathbf {x} }$

수신기는 H와 r을 곱해 신드롬 벡터 z를 얻는데, 이 벡터 z는 에러가 발생했는지, 발생했다면 어떤 코드 워드 비트가 발생했는지를 나타낸다. 이 곱셈을 수행하는 중(again, 항목 modulo 2):

${\displaystyle \mathbf {z} =\mathbf {H} \mathbf {r} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}}$

신드롬 z는 null 벡터(null vector)이므로 수신자는 오류가 발생하지 않았다고 단정할 수 있다. 이 결론은 데이터 벡터에 G를 곱하면 H의 커널인 벡터 서브공간으로 기초변화가 일어난다는 관측에 근거한다.전송 중에 아무 일도 일어나지 않는 한 r은 H의 커널에 남아 있고 곱셈은 null 벡터를 산출한다.

오류수정

그렇지 않으면 단일 비트 오류가 발생했다고 가정해 보십시오. 수학적으로 우리는 글을 쓸 수 있다.

${\displaystyle \mathbf {r} =\mathbf {x} +\mathbf {e} _{i}}$

modulo_i $2{\displaystyle {}_{}}$, ${\displaystyle {\mathrm{여기}}_{}}$서$$e는 i t h {\displaystyle $i_{th}$ 단위$$ 벡터, 즉 ${\displaystyle 1^{}}$부터 ${\displaystyle {\mathrm{계산}}^{}}$하는$$i t h {\$displaystyle$ i$^\{$th}}에 1이 있는 제로 벡터다.

${\displaystyle \mathbf {e} _{2}={\pmatrix}0\\\1\\0\\\0\\nd{pmatrix}}}}$

따라서 위의 표현은 i $t{\displaystyle {}^{}}$ ${\displaystyle h^{}}$ ${\$ 위치에$$ 단일 비트 오류를 나타낸다.

자, 이 벡터에 H를 곱하면:

${\displaystyle \mathbf {Hr} =\mathbf {H} \left(\mathbf {x} +\mathbf {e} _{i}\오른쪽)=\mathbf {Hx} +\mathbf {He} _{i}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$

x는 전송된 데이터이기 때문에 오류 없는 것이고, 그 결과 H와 x의 산물은 0이다. 그러므로

${\displaystyle \mathbf {Hx} +\mathbf {He} _{i}=\mathbf {0} +\mathbf {He} _{i}}$

$이제{\displaystyle {}^{}}$ i ${\displaystyle t^{}}$ ${\displaystyle h^{}}$ ${\$ 표준 기준$$ 벡터가 있는 H 제품은 H 열을 선택하는데, 우리는 이 H 열이 발생하는 곳에서 오류가 발생한다는 것을 알고 있다.

예를 들어, 비트 #5에 비트 오류를 도입했다고 가정합시다.

${\displaystyle \mathbf {r} =\mathbf {x} +\mathbf {e} _{5}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}+{\begin{pmatrix}0\\0\\0\\0\\1\\0\\0\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}}$

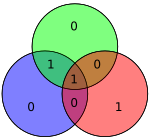
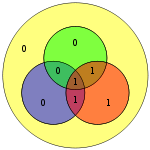
오른쪽의 다이어그램은 빨간색과 녹색 원 안에 비트 오류(파란색 텍스트로 표시)와 생성된 불량 패리티(빨간색 텍스트로 표시)를 나타낸다. 비트 오류는 빨간색, 녹색 및 파란색 원의 패리티를 계산하여 감지할 수 있다. 불량 패리티가 검출되면 불량 패리티 원만 겹치는 데이터 비트는 오류가 있는 비트다. 위의 예에서 빨간색과 녹색 원은 불량한 패리티를 가지고 있으므로 빨간색과 녹색의 교차점에 해당하는 비트는 파란색이 아닌 에러된 비트를 나타낸다.

지금

${\displaystyle \mathbf {z} =\mathbf {Hr} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}={\begin{pmatrix}3\\4\\3\end{pmatrix}}={\begin{pmatrix}1\\0\\1\end{pmatrix}}}$

H의 다섯 번째 열에 해당하는 것이기도 하다. 더욱이 사용된 일반 알고리즘(Hamming code#General algorithm 참조)은 101의 증후군이 5의 이항 값에 해당하도록 구성에서 의도적인 것이었으며, 이는 5번째 비트가 손상되었음을 나타낸다. 따라서, 비트 5에서 오류가 감지되었으며, 수정될 수 있다(단순히 값을 뒤집거나 부정).

${\displaystyle \mathbf {r} _{\text{r}}={\\pmatrix}0\\\1\\\\\\\\\\\\\\\\\nd{pmatrix}}={\pmatrix}0\\1\\1\\end{pmatrix}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

이 수정된 수신 값은 실제로 위에서 전송된 값 x와 일치한다.

디코딩

수신된 벡터가 무오류로 결정되거나 오류가 발생한 경우(제로 또는 1비트 오류만 가능하다고 가정) 수정되면 수신된 데이터를 원래의 4비트로 다시 디코딩해야 한다.

먼저 행렬 R:

${\displaystyle \mathbf {R} ={\begin{pmatrix}0&0&0&0&0&0&0&0&0&0&0&0&0&0&0&\\nd{pmatrix}}}}}$

그런 다음 수신된 값 p는_r Rr과 동일하다. 위의 실행 예제 사용

${\displaystyle \mathbf {p_{r}} ={\begin{pmatrix}0&0&1&0&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}}$

다중 비트 오류

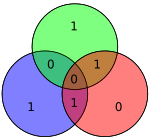
이 방법을 사용하여 단일 비트 오류만 수정할 수 있다는 것을 보여주는 것은 어렵지 않다. 또는 해밍 코드는 오류가 발생할 때마다 H 제품이 0이 아니라는 것만으로 싱글 비트 및 더블 비트 오류를 검출하는 데 사용할 수 있다. 인접한 다이어그램에서는 비트 4와 5가 뒤집혔다. 이는 패리티가 유효하지 않은 원(녹색)을 하나만 산출하지만 오류를 복구할 수 없다.

그러나 해밍(7,4)과 유사한 해밍 코드는 단일 비트 오류와 2비트 오류를 구분할 수 없다. 즉, 2비트 오류는 1비트 오류와 동일하게 나타난다. 2비트 오류에 대해 오류 보정을 수행하면 결과가 잘못된다.

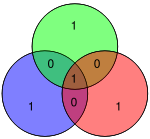
마찬가지로 해밍 코드는 임의의 3비트 오류를 감지하거나 복구할 수 없다. 도표를 생각해 보십시오. 녹색 원(빨간색)에 있는 비트가 1이면 패리티 검사에서 null 벡터가 반환되어 코드 워드에 오류가 없음을 나타냄.

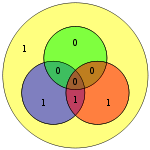
모든 암호

소스가 4비트에 불과하기 때문에 16개의 가능한 전송 단어만 있을 뿐이다. 추가 패리티 비트를 사용할 경우 8비트 값이 포함된다(7, 추가 패리티 비트가 있는 해밍(7,4) 코드 참조). (데이터 비트는 파란색으로 표시되고, 패리티 비트는 빨간색으로 표시되며, 추가 패리티 비트는 노란색으로 표시된다.)

데이터 ${\displaystyle({\color}d_{1},{\color {blue}d_{2}},{\color {blue}d_{3},{\color {blue}d_{4}}}}}}}}}}}}$	해밍(7,4)		추가 패리티 비트가 있는 해밍(7,4) (해밍(8,4))
	전송됨 ${\displaystyle({\color}p_{1},{\color {red}p_{2}},{\color {blue}d_{3}},{\color {blue}d_{3},{\color {blue}d_{4}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}})$	도표	전송됨 ${\displaystyle ({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}},{\color {green}p_{4}})}$	도표
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101
1010	1011010		10110100
0110	1100110		11001100
1110	0010110		00101101
0001	1101001		11010010
1001	0011001		00110011
0101	0100101		01001011
1101	1010101		10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110
1111	1111111		11111111

격자₇

해밍(7,4) 코드는 E₇ 격자와 밀접하게 연관되어 있으며, 사실, 그 이중 격자₇^∗ E(E와₇ 유사한 구조는 이중 코드[7,3,4]₂를 사용한다)를 구성하는 데 사용할 수 있다. 특히 모든 벡터 x in Z에⁷ x congruent (modulo 2)를 해밍(7,4), 코드 워드 (7,4)에 넣고 1/2로 리스케일링하면 격자 E가₇^∗ 된다.

${\displaystyle E_{7}^{*}={\tfrac {1}{\sqrt {2}}}\좌측\{x\in\\in \mathb {Z}^{7}:x{\bmod{2}\in [7,4,3]_{2}\right\}.}$

이것은 격자와 코드 사이의 보다 일반적인 관계의 특별한 예다. 예를 들어 패리티 비트의 추가에서 발생하는 확장(8,4)-해밍 코드는 E₈ 격자와도 관련이 있다. ^[2]

참조

외부 링크

• 해밍 코드의 프로그래밍 문제(7,4)