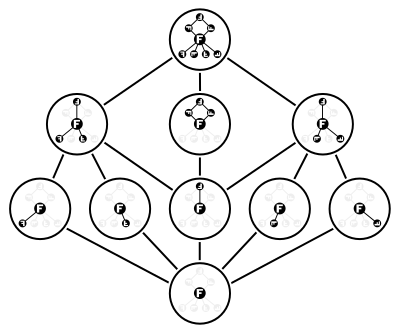
부분군 격자

수학에서 그룹 $G{\displaystyle }$ ${\displaystyle G}$의 부분군 격자는 $부분$ 순서 관계가 포함되도록 설정된 G ${\displaystyle G$의 부분군인 격자다.이 격자에서, 두 부분군의 결합은 그들의 결합에 의해 생성된 부분군이며, 두 부분군의 결합은 그들의 교차점이다.

예

2면체 그룹 Dih는₄ 10개의 하위 그룹을 가지고 있으며, 그 자체와 사소한 하위 그룹을 세고 있다.8개 그룹 요소 중 5개는 순서 2의 하위 그룹을 생성하며, 나머지 2개 비식별 요소는 모두 순서 4의 동일한 순환 하위 그룹을 생성한다.또한, 순서₂ 2 원소의 쌍에 의해 생성된 Z × Z 형식의₂ 두 개의 하위 그룹이 있다.이 10개의 부분군에 의해 형성된 격자는 그림에 나와 있다.

또한 이 예는 그룹의 모든 부분군의 격자가 일반적으로 모듈형 격자가 아님을 보여준다.실제로 이 특별한 격자는 금지된 "펜타곤" N을₅ 하위 격자로 포함하고 있다.

특성.

A ≤ C(C의 A 부분군)와 AB , C = A(B ∩ C)를 갖는 그룹의 A, B 및 C 하위군에 대해, 여기서 곱셈은 하위군의 산물이다.이 속성은 그룹의 모듈형 속성(Aschbacher 2000) 또는 (Dedekind's) 모듈형 법칙(Robinson 1996, Cohn 2000)으로 불려왔다.두 정규 부분군의 경우 제품이 실제로 두 개의 정규 부분군을 포함하는 가장 작은 부분군이기 때문에, 정규 부분군은 모듈형 격자를 형성한다.

래티스 정리는 집단의 부분군 격자와 그 인용구 사이의 갈루아 연결을 설정한다.

Zassenhaus 보조정리기는 부분군 격자 안의 인용문과 제품의 특정 조합 사이에 이형성을 제공한다.

일반적으로 모든 격자는 일부 집단의 부분군 격자 하위 격자 하위 격자 하위 격자에 대해 이형성이라는 점에서 부분군 격자 모양에 제한이 없다.또한, 모든 유한 격자는 일부 유한 집단의 부분군 격자 하위 격자 하위 격자 하위 격자와 이형성이 있다(Schmidt 1994, 페이지 9).

특성 격자

특정 속성을 가진 부분군은 격자를 형성하지만 다른 속성은 그렇지 않다.

• 정상 부분군은 항상 모듈형 격자를 형성한다.사실 격자가 모듈화됨을 보증하는 본질적인 속성은 부분군이 서로 통근하는 것, 즉 퀘이노말 부분군이라는 것이다.
• Nilpotent 정규 부분군은 격자를 형성하며, 이것은 피팅의 정리 내용물의 일부다.
• 일반적으로 모든 Fitting 클래스 F의 경우, 하위 정규 F 하위 그룹과 일반 F 하위 그룹이 모두 래치를 형성한다.여기에는 위와 같은 F와 함께 Nilpotent 그룹의 클래스가 포함되며, F와 같은 다른 예도 포함된다.집단의 종류는 이형성, 부정규격 부분군 및 부정규격 부분군의 생산물에서 닫히면 피팅 클래스라고 한다.
• 중심 부분군은 격자를 형성한다.

그러나 유한 부분군이나 비틀림 부분군은 격자를 형성하지 않는다. 예를 들어 자유 $제품{\displaystyle \mathbf{}}$ Z${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle Z\mathbf{}}$∗ Z${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle Z\mathbf{}}$\$displaystyle \mathbf {Z} /2\mathbf {Z} *\mathbf${Z} *\mathbf /$2\mathbf {Z}은$두 개의 비틀림 요소에 의해 생성되지만$$ 무한하며 무한하다.

정상 하위그룹이 모듈형 격자를 형성한다는 사실은 보다 일반적인 결과의 특별한 경우로서, 즉 어떤 몰트세프 품종(군집단이 예시인 경우)에서 합성의 격자는 모듈형(Kearnes & Kiss 2013)이라는 것이다.

부분군 격자별로 그룹 특성 지정

부분군의 격자에 관한 격자 이론적 정보는 때때로 외이스테인 오레(1937, 1938)의 연구로 거슬러 올라가는 생각인 원래의 집단에 대한 정보를 추론하는 데 사용될 수 있다.예를 들어, Ore가 증명했듯이, 집단의 격자가 분배적인 경우에만 집단은 국지적으로 순환한다.격자가 오름차순 체인 조건을 추가로 만족하면 그룹이 순환한다.

부분군 격자가 보완 격자인 집단을 보완집단(Zacher 1953)이라고 하며, 부분군 격자가 모듈형 격자인 집단을 이와사와 집단 또는 모듈형 집단(Iwasawa 1941)이라고 한다.이러한 유형의 격자-이론적 특성화는 해결 가능한 그룹과 완벽한 그룹(Suzuki 1951)에도 존재한다.

참조

• Aschbacher, M. (2000). Finite Group Theory. Cambridge University Press. p. 6. ISBN 978-0-521-78675-1.
• Baer, Reinhold (1939). "The significance of the system of subgroups for the structure of the group". American Journal of Mathematics. The Johns Hopkins University Press. 61 (1): 1–44. doi:10.2307/2371383. JSTOR 2371383.
• Cohn, Paul Moritz (2000). Classic algebra. Wiley. p. 248. ISBN 978-0-471-87731-8.
• Iwasawa, Kenkiti (1941), "Über die endlichen Gruppen und die Verbände ihrer Untergruppen", J. Fac. Sci. Imp. Univ. Tokyo. Sect. I., 4: 171–199, MR 0005721
• Kearnes, Keith; Kiss, Emil W. (2013). The Shape of Congruence Lattices. American Mathematical Soc. p. 3. ISBN 978-0-8218-8323-5.
• Ore, Øystein (1937). "Structures and group theory. I". Duke Mathematical Journal. 3 (2): 149–174. doi:10.1215/S0012-7094-37-00311-9. MR 1545977.
• Ore, Øystein (1938). "Structures and group theory. II". Duke Mathematical Journal. 4 (2): 247–269. doi:10.1215/S0012-7094-38-00419-3. hdl:10338.dmlcz/100155. MR 1546048.
• Robinson, Derek (1996). A Course in the Theory of Groups. Springer Science & Business Media. p. 15. ISBN 978-0-387-94461-6.
• Rottlaender, Ada (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen". Mathematische Zeitschrift. 28 (1): 641–653. doi:10.1007/BF01181188. S2CID 120596994.
• Schmidt, Roland (1994). Subgroup Lattices of Groups. Expositions in Math. Vol. 14. Walter de Gruyter. ISBN 978-3-11-011213-9. Ralph Freese의 Bull.AMS 33(4): 487–492.
• Suzuki, Michio (1951). "On the lattice of subgroups of finite groups". Transactions of the American Mathematical Society. American Mathematical Society. 70 (2): 345–371. doi:10.2307/1990375. JSTOR 1990375.
• Suzuki, Michio (1956). Structure of a Group and the Structure of its Lattice of Subgroups. Berlin: Springer Verlag.
• Yakovlev, B. V. (1974). "Conditions under which a lattice is isomorphic to a lattice of subgroups of a group". Algebra and Logic. 13 (6): 400–412. doi:10.1007/BF01462952. S2CID 119943975.
• Zacher, Giovanni (1953). "Caratterizzazione dei gruppi risolubili d'ordine finito complementati". Rendiconti del Seminario Matematico della Università di Padova. 22: 113–122. ISSN 0041-8994. MR 0057878.

외부 링크

• 부분군 격자의 PlanetMath 항목
• 예제: 대칭 그룹 S4의 부분군 격자