쌍곡선 운동(상대성)

쌍곡선 운동은 민코프스키 다이어그램에서 시각화할 수 있습니다. 민코프스키 다이어그램에서는 가속 입자의 움직임이

X(\

display

style X

)

축을

X

따릅니다

.각 쌍곡선은 식 (2)에서 x

c=1,\alpha =1

±

x=\pm c^{2}/\alpha

/

\eta =\alpha \tau /c

x=\pm c^{2}/\alpha

{\

displaystyle

x

=\pm

c

^{2}/\alpha }

\eta =\alpha \tau /c

\eta =\alpha \tau /c

=

c=1,\alpha =1

1

\eta =\alpha \tau /c

{\

display c= 1,\alpha

\eta =\alpha \tau /c

1

)에

c=1,\alpha =1

정의됩니다.

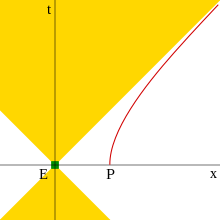
쌍곡선 운동은 특수 상대성 이론에서 일정한 적절한 가속도를 가진 물체의 운동이다.이것은 시공간을 통과하는 물체의 경로를 설명하는 방정식이 적절한 관성(비가속) 프레임을 나타내는 민코프스키 다이어그램에 그래프로 그려졌을 때 볼 수 있는 쌍곡선이기 때문에 쌍곡선 운동이라고 불립니다.이 동작에는 몇 가지 흥미로운 특징이 있는데,^[1] 그 중 다이어그램에서 결론을 내릴 수 있듯이 충분한 선두 출발이 주어지면 광자를 앞지를 수 있다는 것이다.

역사

헤르만 민코프스키(1908)는 세계선상의 점과 4가속도의 크기 사이의 관계와 "곡선 쌍곡선"(독일어: Krümungshyperbel)^[2]을 보여주었다.Born 강성의 맥락에서 Max Born(1909)은 그 후 "과잉 운동"이라는 용어를 만들었습니다(독일어:하이퍼벨베궁(Hyperbelbewegong)은 4가속도의 일정한 크기의 경우, 쌍곡선 운동 하전 입자에 대한 자세한 설명을 제공하고, 이에 대응하는 "하이퍼볼리쉬 베슐레우니테스 베주그 시스템"^[3]을 도입했다.보른의 공식은 Arnold Sommerfeld (1910)^[4]에 의해 단순화되고 확장되었다.초기 리뷰는 막스 폰 라우에(1911, 1921년)^[5] 또는 볼프강 파울리(1921년)^[6]의 교과서를 참조한다.Galeriu(2015)^[7] 또는 Gourgoulhon(2013)^[8] 및 가속(특수 상대성 이론) 참조#역사.

월드라인

입자의 적절한 $(\displaystyle\alpha)$ 는 $\alpha$ 입자가 하나의 관성 기준 프레임에서 다른 프레임으로 가속할 때 "느끼는" 가속도로 정의됩니다.적절한 가속도가 운동 라인에 평행하게 방향일 경우, 이는 특수 $a=du/dT$ 이론 a $a=du/dT$ $a=du/dT$ / $a=du/dT$ T $a=du/dT$ { $displaystyle$ a= $du/d$ }의 일반적인 3가속도와 관련이 있습니다. $T}$ 기준 $a=du/dT$

\alpha =\flac ^{3}a = flac {1} {\left(1-u^{2}/c^{2}\right} {\flac {du} {d}T}},

$u$ 서 $u$ {\ $displaystyle$ u $u$ }는 입자의 순간 속도, ${\$ {\ $displaystyle \gamma}$ 는 $\gamma$ 로렌츠 계수, $c$ {\ $displaystyle$ c $}$ 는 $c$ 빛의 속도, $T$ {\ $displaystyle$ T $}$ 는 $T$ 좌표 시간입니다.운동방정식을 풀면 $좌표시간$ T(\ $displaystyle$ T $)$ 와 $T$ $θ(\$ displaystyle \ $tau$ 로 표현될 수 있습니다.간소화를 위해 시간, 위치 및 속도의 모든 초기값을 0으로 설정할 수 있습니다.^[5]^[6]^[9]^[10]^[11]이렇게 하면 다음과 같습니다.

{array} {c} {\begin{aligned} u(T)&=frac {1+\sqrt {1+\leftfrac} {c}} {{2}}}}\&=c\tanh \left(\operatorname {arh} {arh} {arh} {\fright}\&=frac {c^{2}}{\alpha}}\left(\cosh \left(\operatorname {arsinh}\frac {alpha T}{c}\right)-1\right)\\c\flac(T)&=flac {c^{2}}{\alpha}}\ln \flac {1+\leftfrac {c}{c}}+{\flac {alpha T}{c}}\right}\flac {\flac {c}\flac {\flac}\fright}\&=parcfrac {c^{2}}{\alpha}}\operatorname {arsinh}{arsinh}{\end{aligned}}&{\begin{aligned}u(\tau)&=c\tanh {c}\\\\\x(\tau){c}{frac}{c}{c}}\\cT(\tau)&=synh {c^{2}}{\alpha}}{c}\sinh {frac {frac \alpha \frac }{c}\\\\end {aligned}}\end{array}}

(1)

$\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ + $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ / $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ α ) $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ - $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ / $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ 2 $\left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}$ ( \ $displaystyle \$ left ( $X$ + $c^$ { $2}$ / \ $alpha$ \ $right$ )^2 $} -$ c $^{2$ } $T^{2}=c^{4}/\alpha ^{2$ 시간 T의 쌍곡선 및 공간 위치 $변수$ X(\ $displaystyle$ X $X$ 입니다. 이 경우 가속 객체는 시간 $T=0$ $T=0$ $(\$ $displaystyle$ X $=0$ $T=0$ 에서 $X=0$ X $X=0$ $(\$ $displaystyle$ T $=0)$ 에 $X=0$ 합니다. 대신, 0과 다른 초기 공식이 있는 경우,그는 다음을 형성한다.^[12]^[13]^[14]

{\displaystyle{\scriptstyle{\begin{배열}(T)&, ={\frac{u_{0}\gamma(T}{\sqrt{1+\left({\frac{u_{0}일 경우 \gamma_{0}일 경우 +\alpha T}{c}}\right)^{2}}}}\quad \\&, =c\tanh \left\{\operatorname{arsinh}\left({\frac{u_{0}일 경우 \gamma_{0}일 경우 +\alpha T}{c}}\right)\right\}\\X(T)&, =X_{0}+{\frac{{2c^}}{\alpha}}\left({\sqrt{1+\left(.{\frac{u_{0}\gamma _{0}+\alpha T}{c}\right)^{2}-\gamma _{0}\right)\\&, =X_{0}+{\frac{{2c^}}{\alpha}}\left\{\cosh \left[\operatorname{arsinh}\left({\frac{u_{0}일 경우 \gamma_{0}일 경우 +\alpha T}{c}}\right)\right]-\gamma_{0}\right\}\\c\tau(T)&, =c\tau _{0}+{\frac{{2c^}}{\alpha}}\ln \left({\frac{{\sqrt{c^{2}+\left(u_{0}일 경우 \gamma_{0}일 경우 +\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}일 경우 \right)\gamma_{0}}}\r.밤))\&, =c\tau _{0}+{\frac{{2c^}}{\alpha}}\left\{\operatorname{arsinh}\left({\frac{u_{0}일 경우 \gamma_{0}일 경우 +\alpha T}{c}}\right)-\operatorname{artanh}\left({\frac{u_{0}}{c}}\right)\right\}\end{정렬}}&{\begin{정렬}(\tau)&, =c\tanh \left\{\operatorname{artanh}\left({\frac{u_{0}}{c}}\right)+{\frac{\alpha)}{c}}\right\}\\\\X(\tau)&.앰프, =X_{0}+{\fraC{c^{2}}{\alpha}}\left\{\cosh \left[\operatorname{artanh}\left({\frac{u_{0}}{c}}\right)+{\frac{\alpha \tau}{c}}\right]-\gamma_{0}\right\}\\\\cT(\tau)&, =c.T_{0}+{\frac{{2c^}}{\alpha}}\left\{\sinh \left[\operatorname{artanh}\left({\frac{u_{0}}{c}}\right)+{\frac{\alpha \tau}{c}}\right]-{\frac{u_{0}\gamma _{0}}{c}}\right\}\end{정렬}}년.end {array}}}}:

신속성

쌍곡선 운동의 세계선(앞으로 적절한 시간의 함수로 작성될 예정)은 몇 가지 방법으로 단순화할 수 있습니다.예를 들어, 표현은

X=frac {c^{2}}{\alpha }}\left(\cosh {\frac\frac}{c}-1\오른쪽)

$c^{2}/\alpha$ $c^{2}/\alpha$ / $c^{2}/\alpha$ α (\ $displaystyle c^{2$ }/\ $alpha$ })의 공간적 이동에 노출될 수 있습니다.

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

cosh

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

c

X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}

{

displaystyle

X =

snap frac

{ c^{

2}}

{\

alpha

}}\

cosh {frac {\

alpha \

frac

^[15]

관찰자가 $X=c^{2}/\alpha$ X $T=0$ $T=0$ $X=c^{2}/\alpha$ / $X=c^{2}/\alpha$ (\ $displaystyle$ X $=c^{2}/\alpha }$ 에 $X=c^{2}/\alpha$ 있는 시간 $T=0$ = $T=0$ 0 {\ $displaystyle$ T $=0$ 또한 x $x=c^{2}/\alpha$ $x=c^{2}/\alpha$ $x=c^{2}/\alpha$ α (\ $displaystyle$ x= $c^{2}/\alpha }$ 를 $x=c^{2}/\alpha$ $x=c^{2}/\alpha$ 하고 $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ = $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ u c u u u u u by by by by u u by by by by by by c c c by c c c c c by $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ = $\eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}$ by by by by by by by\ $frac {alpha \filename$ }{ $c$ ^[14] 쌍곡선 운동의 방정식은 다음과 같이 감소합니다^[4]^[16] $.$

cT=x\sinh \eta,\display X=x\cosh \eta

(2)

$X^{2}-c^{2}T^{2}=x^{2}$ $X^{2}-c^{2}T^{2}=x^{2}$ - c $X^{2}-c^{2}T^{2}=x^{2}$ $X^{2}-c^{2}T^{2}=x^{2}$ 2 $X^{2}-c^{2}T^{2}=x^{2}$ $X^{2}-c^{2}T^{2}=x^{2}$ 2 {\ $displaystyle$ X $^{2}-c^{$ } 사용 $T^{2}=x^{2$

쌍곡선 운동 하전 입자

출생(1909년),^[3] 소머펠트(1910년),^[4] 폰 라우에(1911년),^[5] 파울리(1921)^[6]는 또한 쌍곡선 ^[7]운동으로 하전 입자의 전자장에 대한 방정식을 공식화했다.이는 헤르만 본디 & 토마스 골드(^[17]1955년)와 풀턴 & 로를리히(1960년)^[18]^[19]에 의해 확대되었다.

디스플레이 스타일E_{\rho '}=&{\frac {left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime3}}\E_{z'}=&{\frac {-left(4e/\alpha ^{2}\right)1/\alpha ^2+rprime}2^{\rprime}2}2+t}2^{\prime}E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}=&{\frac(왼쪽(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime3}}\xi '=&{\prime rt { 1/alpha ^{2}+t^{\rho ^{\prime}^{\prime}^{\prime}) 2-{\prime}^{\prime}2-{\prime}2-}\prime}

이것은 논란이 되고^[20]^[21] 있는 질문, 영구 쌍곡선 운동에서의 전하가 방사되는지 여부, 그리고 이것이 등가 원리와 일치하는지 여부 - 비록 이상적인 상황에 관한 것일지라도, 영구 쌍곡선 운동은 불가능하기 때문에.Born(1909)이나 Pauli(1921)와 같은 초기 저자는 방사선이 발생하지 않는다고 주장한 반면, Bondi & Gold와^[17] Fulton & Rohrlich와^[18]^[19] 같은 후기 저자는 방사선이 실제로 발생한다는 것을 보여주었다.

적절한 기준 프레임

E를 통과하는 광 경로는 쌍곡선 운동에서 관찰자 P의 명백한 사건 지평선을 표시합니다.

쌍곡선 운동의 방정식 (2)에서 x $(\displaystyle$ x $)$ 는 $x$ 일정하고, radiity $\eta$ (\ $displaystyle \eta)$ 는 $\eta$ 가변적이었다.단,^[16] Sommerfeld가 지적한 바와 같이x를 $x$ $x$ 로 정의하면서 $θ$ \ $displaystyle$ $\eta$ 를 $\eta$ 일정하게 할 수 있습니다.즉, 방정식이 쌍곡 좌표 $(x,y,z,\eta )$ $(x,y,z,\eta )$ $)$ { $displaystyle(x,y,z,\eta)}$ 을 $(x,y,z,\eta )$ 가진 가속체의 동시 정지 형태를 나타내는 변환이 됩니다.

\displaystyle cT=x\sinh \eta,\display X=x\cosh \eta,\display Y=y,\quad Z=z}

이 변환에 의해 적정 시간은 하이퍼볼릭 가속 프레임의 시간이 된다.일반적으로 린들러 좌표(비슷한 변형을 코틀러-뮐러 좌표 또는 라스 좌표라고 함)라고 불리는 이러한 좌표는 페르미 좌표 또는 고유 좌표의 특수한 경우로 볼 수 있으며, 종종 언루 효과와 함께 사용됩니다.이러한 좌표를 사용하여 쌍곡선 운동 관측자는 어떠한 신호도 도달할 수 없는 명백한 사건 지평선을 가지고 있는 것으로 밝혀졌다.

특수 등각 변환

쌍곡선 운동에서 기준 프레임을 정의하는 덜 알려진 방법은 반전, 변환 및 다른 반전으로 구성된 특수 등각 변환을 사용하는 것입니다.이것은 민코프스키 공간의 게이지 변환으로 해석되지만, 일부 저자는 이를 가속도 변환으로 대체적으로 사용한다(중요한 과거 ^[22]조사는 카스트럽 참조).그것은 형태를 가지고 있다.

{\displaystyle X^{\mu } = flac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}}x^{2}}}}}:

$x^{\mu }=(t,x)$ μ $=$ ( $x^{\mu }=(t,x)$ , $x^{\mu }=(t,x)$ ) { $displaystyle$ x^ { \ $mu$ } $=$ ( t , $x$ $x^{\mu }=(t,x)$ ) $a^{\mu }=(0,-\alpha /2)$ } $x=0$ further further further further further further further further further by by by by $x=0$ $a^{\mu }=(0,-\alpha /2)$ 0 （ $displaystyle$ x $a^{\mu }=(0,-\alpha /2)$ $0$ $x=0$ $a^{\mu }=(0,-\alpha /2)$ the the the the the the $theifyingifyingifyingifyingifying$ ^[23] ifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifyingifying = ( 0 , - 、 $a^{\mu }=(0,-\alpha /2)$ , - $a^{\mu }=(0,-\alpha /2)$ / $setting$ / / / / / / / / / / / / / / / / / / / / / / / / $a^{\mu }=(0,-\alpha /2)$ the

T=paramfrac {t}{1-{\frac {1}{4}\alpha {}{2}},\param X=paramfrac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {2}^{2}\right)}}

그 쌍곡선(X1/α −)으로 2− T2=1/α 2{\displaystyle \left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}}. 그것은으로를 t=±(x+2/α){\displaystyle t=\pm(x+2/\alpha)}은 시간이 된에 풀턴&Rohrlich&Witten[23]발언이 사람에 떨어져 지내에서 이. 한계,Kastrup^[22](가속도 해석에 매우 비판적)은 이것이 이 해석의 이상한 결과 중 하나라고 말한다.

메모들

^ 미스너, 손 & 휠러 1973, 6장
^ Minkowski, Hermann (1909). "Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu Köln am 21. September 1908" [Wikisource translation: Space and Time]. Jahresbericht der Deutschen Mathematiker-Vereinigung. Leipzig.
^ ^a ^b Born, Max (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips" [Wikisource translation: The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909AnP...335....1B. doi:10.1002/andp.19093351102.
^ ^a ^b ^c Sommerfeld, Arnold (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Wikisource translation: On the Theory of Relativity II: Four-dimensional Vector Analysis]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910AnP...338..649S. doi:10.1002/andp.19103381402.
^ ^a ^b ^c 1911년 초판, 1913년 제2판, 1919년 제3판von Laue, M. (1921). Die Relativitätstheorie, Band 1 (fourth edition of "Das Relativitätsprinzip" ed.). Vieweg. pp. 89–90, 155–166..
^ ^a ^b ^c Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
영어:
^ ^a ^b Galeriu, C. (2017) [2015]. "Electric charge in hyperbolic motion: the early history". Archive for History of Exact Sciences. 71 (4): 1–16. arXiv:1509.02504. doi:10.1007/s00407-017-0191-x. S2CID 118510589.
^ Gourgoulhon, E. (2013). Special Relativity in General Frames: From Particles to Astrophysics. Springer. p. 396. ISBN 978-3642372766.
^ Møller, C. (1955). The theory of relativity. Oxford Clarendon Press. pp. 74–75.
^ Rindler, W. (1977). Essential Relativity. Springer. pp. 49–50. ISBN 354007970X.
^ PhysicalFAQ(2016), "상대론적 로켓", 외부 링크 참조
^ Gallant, J. (2012). Doing Physics with Scientific Notebook: A Problem Solving Approach. John Wiley & Sons. pp. 437–441. ISBN 978-0470665978.
^ Müller, T., King, A., & Adis, D. (2006). "A trip to the end of the universe and the twin "paradox"". American Journal of Physics. 76 (4): 360–373. arXiv:physics/0612126. Bibcode:2008AmJPh..76..360M. doi:10.1119/1.2830528. S2CID 42983285.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ ^a ^b Fraundorf, P. (2012). "A traveler-centered intro to kinematics": IV–B. arXiv:1206.2877. Bibcode:2012arXiv1206.2877F. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Pauli (p. 628)는 x $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ t a ch t $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ ${$ $displaystyle$ x $^{4$ }= $a\operatorname {ch}$ { $frac$ { $ct}$ {a $}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ 을 $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $a={\frac {c^{2}}{b}}$ 했다. $a={\frac {c^{2}}{b}}$ 서 a $=$ $a={\frac {c^{2}}{b}}$ b { $displaystyle a = c^{2$ }} { $b}}$ }
^ ^a ^b Sommerfeld(1910), 페이지 670-671은 x $l=r\sin(\varphi )$ $x=r\cos(\varphi )$ $l=ict$ $x=r\cos(\varphi )$ ( $x=r\cos(\varphi )$ \ $display$ $style$ x $= r$ \ $cos$ ( \ $varphi$ ) $l=r\sin(\varphi )$ } $l=r\sin(\varphi )$ $l=r\sin(\varphi )$ $=$ r $l=r\sin(\varphi )$ ( \ varphi )의 $x=r\cos(\varphi )$ $l=r\sin(\varphi )$ $l=r\sin(\varphi )$ 을 사용했으며, 상상의 $i\psi$ i $i\psi$ \ $display style$ i $\psi$ $=$ \ $sin$ $l=r\sin(\varphi )$ ( \ $varphi )$ $x=r\cos(\varphi )$ display $i\psi$ )는 l $l=ict$ ldisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay
^ ^a ^b Bondi, H., & Gold, T. (1955). "The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration". Proceedings of the Royal Society of London. 229 (1178): 416–424. Bibcode:1955RSPSA.229..416B. doi:10.1098/rspa.1955.0098. S2CID 121563673.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ ^a ^b Fulton, Thomas; Rohrlich, Fritz (1960). "Classical radiation from a uniformly accelerated charge". Annals of Physics. 9 (4): 499–517. Bibcode:1960AnPhy...9..499F. doi:10.1016/0003-4916(60)90105-6.
^ ^a ^b Rohrlich, Fritz (1963). "The principle of equivalence". Annals of Physics. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. doi:10.1016/0003-4916(63)90051-4.
^ Stephen Lyle (2008). Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle. Springer. ISBN 978-3540684770.
^ Øyvind Grøn (2012). "Review Article: Electrodynamics of Radiating Charges". Advances in Mathematical Physics. 2012: 528631. doi:10.1155/2012/528631.
^ ^a ^b Kastrup, H. A. (2008). "On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics". Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730. Bibcode:2008AnP...520..631K. doi:10.1002/andp.200810324. S2CID 12020510.
^ ^a ^b Fulton, T., Rohrlich, F., & Witten, L. (1962). "Physical consequences of a co-ordinate transformation to a uniformly accelerating frame". Il Nuovo Cimento. 26 (4): 652–671. Bibcode:1962NCim...26..652F. doi:10.1007/BF02781794. S2CID 121467786.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

레퍼런스

Leigh Page (Feb 1936). "A New Relativity. Paper I. Fundamental Principles and Transformations Between Accelerated Systems". Physical Review. 49 (3): 254–268. Bibcode:1936PhRv...49..254P. doi:10.1103/PhysRev.49.254.
Leigh Page & Norman I. Adams (Mar 1936). "A New Relativity. Paper II. Transformation of the Electromagnetic Field Between Accelerated Systems and the Force Equation". Physical Review. 49 (6): 466–469. Bibcode:1936PhRv...49..466P. doi:10.1103/PhysRev.49.466.
Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, Chapter 6, ISBN 0-7167-0344-0
Rindler Wolfgang (1960). "Hyperbolic Motion in Curved Space Time". Physical Review. 119 (6): 2082–2089. Bibcode:1960PhRv..119.2082R. doi:10.1103/PhysRev.119.2082.
Ludwik Silberstein(1914):상대성이론 190쪽
Naber, Gregory L., The Geometry of Minkowski Spacetime, Springer-Verlag, 1992, 뉴욕.ISBN 0-387-97848-8(하드커버), ISBN 0-486-43235-1(도버 페이퍼백판).페이지 58~60.

외부 링크

물리 FAQ: 상대론적 로켓
산술 페이지:가속 주행, 균일하게 가속되는 충전은 방사됩니까?

[1] 미스너, 손 & 휠러 1973, 6장

[2] Minkowski, Hermann (1909). "Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu Köln am 21. September 1908" [Wikisource translation: Space and Time]. Jahresbericht der Deutschen Mathematiker-Vereinigung. Leipzig.

[born-3] Born, Max (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips" [Wikisource translation: The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909AnP...335....1B. doi:10.1002/andp.19093351102.

[sommerfeld-4] Sommerfeld, Arnold (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Wikisource translation: On the Theory of Relativity II: Four-dimensional Vector Analysis]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910AnP...338..649S. doi:10.1002/andp.19103381402.

[laue-5] 1911년 초판, 1913년 제2판, 1919년 제3판von Laue, M. (1921). Die Relativitätstheorie, Band 1 (fourth edition of "Das Relativitätsprinzip" ed.). Vieweg. pp. 89–90, 155–166..

[pauli-6] Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
영어:

[Galeriu-7] Galeriu, C. (2017) [2015]. "Electric charge in hyperbolic motion: the early history". Archive for History of Exact Sciences. 71 (4): 1–16. arXiv:1509.02504. doi:10.1007/s00407-017-0191-x. S2CID 118510589.

[8] Gourgoulhon, E. (2013). Special Relativity in General Frames: From Particles to Astrophysics. Springer. p. 396. ISBN 978-3642372766.

[9] Møller, C. (1955). The theory of relativity. Oxford Clarendon Press. pp. 74–75.

[10] Rindler, W. (1977). Essential Relativity. Springer. pp. 49–50. ISBN 354007970X.

[11] PhysicalFAQ(2016), "상대론적 로켓", 외부 링크 참조

[12] Gallant, J. (2012). Doing Physics with Scientific Notebook: A Problem Solving Approach. John Wiley & Sons. pp. 437–441. ISBN 978-0470665978.

[13] Müller, T., King, A., & Adis, D. (2006). "A trip to the end of the universe and the twin "paradox"". American Journal of Physics. 76 (4): 360–373. arXiv:physics/0612126. Bibcode:2008AmJPh..76..360M. doi:10.1119/1.2830528. S2CID 42983285.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[fraundorf-14] Fraundorf, P. (2012). "A traveler-centered intro to kinematics": IV–B. arXiv:1206.2877. Bibcode:2012arXiv1206.2877F. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[15] Pauli (p. 628)는 x $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ t a ch t $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ ${$ $displaystyle$ x $^{4$ }= $a\operatorname {ch}$ { $frac$ { $ct}$ {a $}}$ $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ 을 $x^{4}=a\operatorname {ch} {\frac {ct}{a}}$ $a={\frac {c^{2}}{b}}$ 했다. $a={\frac {c^{2}}{b}}$ 서 a $=$ $a={\frac {c^{2}}{b}}$ b { $displaystyle a = c^{2$ }} { $b}}$ }

[sommerfeld2-16] Sommerfeld(1910), 페이지 670-671은 x $l=r\sin(\varphi )$ $x=r\cos(\varphi )$ $l=ict$ $x=r\cos(\varphi )$ ( $x=r\cos(\varphi )$ \ $display$ $style$ x $= r$ \ $cos$ ( \ $varphi$ ) $l=r\sin(\varphi )$ } $l=r\sin(\varphi )$ $l=r\sin(\varphi )$ $=$ r $l=r\sin(\varphi )$ ( \ varphi )의 $x=r\cos(\varphi )$ $l=r\sin(\varphi )$ $l=r\sin(\varphi )$ 을 사용했으며, 상상의 $i\psi$ i $i\psi$ \ $display style$ i $\psi$ $=$ \ $sin$ $l=r\sin(\varphi )$ ( \ $varphi )$ $x=r\cos(\varphi )$ display $i\psi$ )는 l $l=ict$ ldisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay

[Bondi-17] Bondi, H., & Gold, T. (1955). "The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration". Proceedings of the Royal Society of London. 229 (1178): 416–424. Bibcode:1955RSPSA.229..416B. doi:10.1098/rspa.1955.0098. S2CID 121563673.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[Fulton-18] Fulton, Thomas; Rohrlich, Fritz (1960). "Classical radiation from a uniformly accelerated charge". Annals of Physics. 9 (4): 499–517. Bibcode:1960AnPhy...9..499F. doi:10.1016/0003-4916(60)90105-6.

[Rohrlich-19] Rohrlich, Fritz (1963). "The principle of equivalence". Annals of Physics. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. doi:10.1016/0003-4916(63)90051-4.

[Lyle-20] Stephen Lyle (2008). Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle. Springer. ISBN 978-3540684770.

[Gron3-21] Øyvind Grøn (2012). "Review Article: Electrodynamics of Radiating Charges". Advances in Mathematical Physics. 2012: 528631. doi:10.1155/2012/528631.

[kastrup-22] Kastrup, H. A. (2008). "On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics". Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730. Bibcode:2008AnP...520..631K. doi:10.1002/andp.200810324. S2CID 12020510.

[Fulton2-23] Fulton, T., Rohrlich, F., & Witten, L. (1962). "Physical consequences of a co-ordinate transformation to a uniformly accelerating frame". Il Nuovo Cimento. 26 (4): 652–671. Bibcode:1962NCim...26..652F. doi:10.1007/BF02781794. S2CID 121467786.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

Search