적정가속

상대성 이론에서 적절한 가속도는^[1] 물체가 경험하는 물리적 가속도(즉, 가속도계에 의한 측정 가능한 가속도)이다. 따라서 측정 대상 물체에 대해 잠시 정지해 있는 자유 낙하 또는 관성 관측자에 상대적인 가속이다. 따라서 중력은 관성 관찰자에게 작용하기 때문에 적절한 가속도가 반드시 떨어져야 하기 때문에 중력은 적절한 가속을 유발하지 않는다. 관성 관측자는 항상 0의 적절한 가속도를 갖는다는 것이 골자다.

적절한 가속도는 좌표계 선택에 따라 달라지는 좌표 가속도와 대비된다(특수 상대성에서는 3 가속도 참조).

특수상대성이론의 표준 관성 좌표에서 단방향 운동에서 적절한 가속도는 조정 시간에 대한 적절한 속도의 변화율이다.

물체가 순간적으로 정지해 있는 관성 프레임에서 적절한 가속도 3벡터는 0시간 성분과 결합하여 물체의 4가속도를 산출하여 적절한 가속도의 로렌츠-인바리안을 만든다. 따라서 개념은 (i) 가속 좌표계, (ii) 상대론적 속도 및 (iii) 곡선 스페이스타임의 (iii)가 유용하다.

발사 후 가속로켓에서 또는 갠트리에 서 있는 로켓에서조차 적절한 가속도는 탑승자가 느끼는 가속도이며, 이 가속도는 차량이 전달하는 g-힘(힘이 아니라 가속도일 뿐 아니라 가속도일 뿐, 적절한 가속도에 대한 더 많은 논의를 위해 해당 기사를 참조)으로 설명된다.^[2] "중력의 가속" ("중력의 힘")은 어떤 상황에서도 적절한 가속도에 기여하지 않으며, 따라서 지상에 서 있는 관측자들이 느끼는 적절한 가속도는 중력의 "힘"이나 "가속"에 기인한 것이 아니라 지상의 기계적 힘에 기인한다. 지면을 제거하고 관찰자가 자유낙하를 허용하면 관찰자는 좌표 가속을 경험하지만 적절한 가속도는 경험하지 못하므로 g-힘은 경험하지 않는다. 일반적으로 그러한 낙하 또는 궤도에 있는 물체를 포함한 탄도 경로(관성 운동이라고도 함)에 있는 물체는 적절한 가속을 경험하지 않는다(중력장 내 관성 경로에 대한 작은 조력 가속을 무시함). 이 상태는 "무중력"("제로-g") 또는 "자유 낙하"로도 알려져 있으며 무중력 상태를 유발한다.

적절한 가속도는 물체의 적정^[3] 속도(단위 질량 당 순간)가 광도 c의 속도보다 훨씬 작을 경우 평탄한 시간(즉, 중력이 없는 경우)에 관성 좌표계에서 가속도를 조정하기 위해 감소한다. 그러한 상황에서만 좌표 가속이 g-힘으로 완전히 느껴진다(즉, 적절한 가속도, 측정 가능한 무게를 산출하는 가속도라고도 정의됨).

중력이 없지만 선택된 좌표계가 관성적이 아니라 관찰자(가속 로켓의 가속 기준 프레임 또는 원심분리기의 물체에 고정된 프레임 등)와 함께 가속되는 상황에서, 이러한 좌표계의 관측자가 느끼는 g-용기와 그에 상응하는 적절한 가속도는 다음과 같다. 그러한 시스템에서 무게에 저항하는 기계적 힘에 의해 발생한다. 결국 이 중량은 (지구 표면에서와 같이) 중력체와 관련하여 우주에 물체가 고정되어 있는 시스템에서 "중력의 힘"에 의해 생성된 무게와 같은 방식으로, 모든 가속 좌표계에 나타나는 가공의 힘 또는 "내력"에 의해 생성된다.

뉴턴의 법칙 F = m a를 통해 적절한 가속도를 갖는 좌표계의 정지 상태의 질량에 대한 적절한 가속을 유도하기 위해 계산되는 총(기계적) 힘을 적절한 힘이라고 한다. 위에서 본 바와 같이, 적절한 힘은 물체의 "작동 중량"(즉, 물체의 좌표계에서 스프링 스케일과 같은 장치에 의해 측정되는 무게)로 측정되는 반대되는 반응력과 같다. 따라서 물체에 대한 적절한 힘은 항상 측정된 무게와 동일하고 반대다.

예

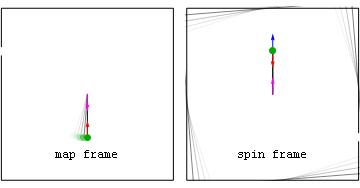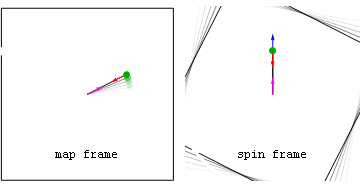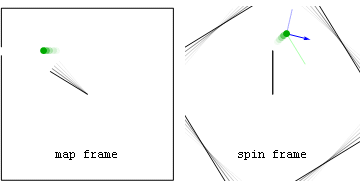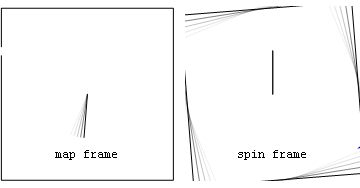
일정한 각도 속도로 회전하는 회전목마를 잡고 있을 때 관찰자는 핸드홀드와 관찰자의 손 사이의 상호 작용으로 인해 반경방향으로 (중심) 적절한 가속을 경험한다. 이것은 회전 좌표 프레임과 연관된 방사상 바깥쪽 기하학적 가속을 취소한다. (회전 프레임의 관점에서) 이 바깥쪽 가속도는 그들이 놓았을 때 좌표 가속이 되어, 그들이 0의 적절한 가속(지오데틱) 경로를 따라 날아가게 할 것이다. 물론 가속되지 않은 관찰자들은 그들의 틀에서 그들의 동등한 적절성과 조정 가속도가 그들이 놓아주었을 때 사라지는 것을 볼 뿐이다.

애니메이션: 회전목마 접지력 상실
회전목마에서 방출된 물체에 대한 적색(빨간색) 및 기하학적(파란색) 가속도의 지도 및 스핀 프레임 관점 지도 프레임 관점에서 보면 위험한 것은 접선 속도다. 스핀 프레임 관점에서 볼 때 위험은 그 대신 기하급수적인 가속도에 있을 수 있다.

마찬가지로 회전하지 않는 행성(및 실제 목적을 위해 지구)에 서 있는 관측자들은 신발 바닥에 지구가 발휘하는 정상적인 힘에 의해 상승하는 적절한 가속을 경험한다. 이것은 좌표계(일명 쉘프레임^[4])의 선택으로 인한 하향 기하급수적인 가속을 취소한다. 그러한 하향 가속도는 그들이 부주의로 절벽에서 떨어져 0의 적절한 가속도(지오데믹 또는 레인프레임) 궤도로 진입할 경우 좌표가 된다.

애니메이션: 절벽에서 굴러 떨어지는 공
절벽에서 굴러 떨어지는 물체에 적합한(빨간색) 가속도와 기하학적(파란색) 가속도의 비와 조개 프레임 관점. 참고: 빗방울의 관점이라기 보다는 공이 절벽 끝에 도달하는 것처럼 궤적이 위로 튀어나오는 트램펄린 점퍼에 가깝다. 쉘 프레임의 관점은 곡선 스페이스타임으로 인한 기하급수적인 가속으로부터 그들을 보호하기 위해 그들의 환경으로부터 조금씩 위로 올라가는 물리적 가속도에 의존하는 행성 거주자들에게 친숙할 수 있다. 처음에 그들에게 마이크로 중력 환경이 무섭게 보일 수 있는 것은 당연하다.

기하학적 가속도(아래 좌표계의 공변량 파생상품의 연결 용어로 인해)는 우리 존재의 모든 온스에 작용하는 반면, 적절한 가속도는 보통 외부 힘에 의해 발생한다. 물리학 입문 과정은 흔히 중력의 하향(기하학) 가속도를 질량 비례력에 의한 것으로 취급한다. 이것은 비가속 프레임의 부지런한 회피와 함께, 그들은 적절한 가속을 다루며 같은 것으로서 가속을 조정할 수 있게 한다.

심지어 물체가 평탄한 시간 동안 장기간 동안 정지 상태에서 일정한 적절한 가속도를 유지하는 경우에도, 나머지 프레임의 관측자들은 좌표 속도가 광속에 접근함에 따라 물체의 좌표 가속도가 감소하는 것을 볼 것이다. 그럼에도 불구하고 그 물체의 적절한 속도가 올라가는 속도는 일정하게 유지된다.

애니메이션: 고속 트립 위/아래
수직 방향의 적절한(빨간색) 가속도/감속도에 대한 지도 프레임 관점 및 좌표(녹색) 여기서 우리의 물체는 먼저 여행자 시계에서 2*c/α의 시간 동안 위쪽으로 가속하는데, 여기서 c는 광속이고 α는 적절한 가속도의 크기(빨간색)이다. 이 첫 번째 다리는 가속도의 크기가 약 1-gee일 경우 약 2년이 걸린다. 그런 다음 이 기간 두 번 동안 아래로 가속(처음에는 감속되었다가 가속)한 다음, 2*c/α 상승 감속하여 원래 높이로 되돌아간다. 좌표 가속도(녹색)는 이 항해의 저속 구간에서만 유의하다는 점에 유의하십시오.

따라서 적절한 가속도와 조정 가속도의^[5] 구별은 다양한 비뉴턴적 관점에서 가속 여행자의 경험을 추적할 수 있게 한다. 이러한 관점에는 가속 좌표계(캐러셀과 같은), 고속(적절한 속도와 조정 시간이 다른 경우) 및 곡면 스페이스타임(지구의 중력과 관련된 경우)이 포함된다.

클래식 어플리케이션

뉴턴 물리학의 관성 좌표계에서 저속에서는 적절한 가속도가 단순히 좌표 가속도 a=dx²/dt와² 같다. 그러나 위에서 검토한 바와 같이, 정지 상태에서 가속하는 자동차나 새총에서 돌멩이가 회전하는 것과 같은 가속 좌표계의 관점에서 세계를 기술하기 위해 (뉴턴의 조언에 반대) 선택한다면 좌표 가속과는 다르다. 만일 중력이 스페이스타임의 곡률에 의해 발생한다는 것을 인식하기로 선택한 경우(아래 참조), 적절한 가속도는 중력장의 좌표 가속도와 다르다.

예를 들어, 물리적 또는 적절한 가속도의 대상인_o 물체는 일정한 가속을_frame 거치는 좌표계의 관찰자에게 다음과 같이 보여진다.

${\displaystyle {\stackrel{}{a}}_{}}$→ ${\displaystyle c_{}}$= a →${\displaystyle {\stackrel{}{}}_{}{o}_{}{}_{}}$- a${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle f_{}}$ ${\displaystyle r_{}}$ ${\displaystyle e_{}}$ ${\$}={\$vec}-{o}-{\vec{a}_{frame$

따라서 객체가 프레임으로 가속하는 경우 프레임에 고정된 관찰자는 가속을 전혀 보지 못할 것이다.

애니메이션: 블록 간 주행
정지 신호에서 다음 신호로 주행하는 차량을 위한 물리적(빨간색) 및 기하학적(파란색) 가속도의 지도 및 차량 프레임 관점 이 그림에서 차량은 정지 신호 후 블록 중간까지 가속되며, 이때 운전자가 가속 페달에서 즉시 브레이크 위로 내려서 다음 멈춤을 취하도록 한다.

마찬가지로, 물리적 또는 적절한 가속을_o 거치는 물체는 각도 속도 Ω으로 회전하는 프레임에서 관측자에게 다음과 같이 좌표 가속도를 갖는다.

${\displaystyle {\vec {a}}_{rot}={\vec {a}}_{o}-{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})-2{\vec {\omega }}\times {\vec {v}}_{rot}-{\frac {d{\vec {\omega }}}{dt}}\times {\vec {$$r}}$ $.$

위의 방정식에서 오른쪽에는 세 개의 기하급수적인 가속 항이 있다. 첫번째"원심 가속도"용어는 레이디얼 위치 r이 아닌 개체의 속도의 두번째"코리올리 가속"용어는 회전 프레임 vrot의 물체의 속도만 위치에 달려 있으며 3"오일러 가속도"기간 위치와 프레임의 angu의 변경의 비율에만 달려 있습니다.l아 속도

뉴턴의 예: 정속 새총

질량이 없는 밧줄 위에서 회전한 후 방출된 돌과 관련된 가속도와 힘을 지도 및 회전 프레임 관점을 만드십시오. 돌 위의 힘은 두 프레임에서 보이는 내부 구심력(빨간색)과 스핀 프레임에서 보이는 기하학적(파란색) 힘을 포함한다. 돌이 풀리기 전에는 푸른 기하학적 힘이 순전히 원심력(방사적으로 바깥쪽을 가리키고 있음)인 반면, 해제 후 기하학적 힘은 원심력과 코리올리스 성분의 합이다. 스핀 프레임에서 해제된 후 원심성 구성 요소(연청색)는 항상 방사형이며, 코리올리스 구성 요소(녹색)는 항상 스핀 프레임 속도에 수직이다. 또한 두 프레임에서 볼 수 있는 것은 뉴턴의 세 번째 법칙 작용이 돌의 구심력에 대한 작용에 의해 발생하는 로프의 닻 지점(마젠타)에 가해지는 힘이다. 발사체 발사 전 돌을 방출하기 전에 다음의 움직임의 대체 분석은 방사 방향에서 작용하는 힘만 고려한다. 두 분석 모두 끈 장력 T=mv2/r을 예측한다. 예를 들어 슬링의 반경이 r=1m, 지도 프레임의 돌의 속도가 초속 v=25m, 돌의 질량 m=0.2kg이면 끈의 장력은 125뉴턴이 된다. 실행 전 맵 프레임 스토리 ${\displaystyle -T_{centripetal}=\Sigma F_{radial}=ma_{radial}=-m{\frac{v^{2}}{r}}}.}$ 여기서 그 돌은 반지름 r의 원형 경로를 따라갈 수 있도록 안쪽으로 계속 가속되는 것으로 보인다. aradial=v2/r의 내부 방사상 가속도는 단일 불균형 구심력 T에 의해 발생한다. 장력력이 불균형하다는 것은 이 틀에서 돌에 가해지는 원심력(방사선)의 힘이 0이라는 것을 의미한다. 출시 전 스핀 프레임 스토리 ${\displaystyle m{\frac{v^{2}}-T_{centripetal}=\Sigma F_{rot}=ma_{rot}=0.}$ 스핀 프레임 관점에서 돌이 내부 구심력(T)과 외부 원심력(mv2/r)의 균형을 경험한다고 말할 수 있는데, 이 힘은 그 프레임의 관점에서 전혀 가속이 되지 않는다. 구심력과 달리, 프레임에 의존하는 원심력은 당신의 모든 온스에 중력이 작용하는 것과 마찬가지로 원석의 모든 부분에 작용한다. 더욱이 원심력 크기는 돌의 질량에 비례하므로 가속을 일으킬 수 있다면 가속도는 질량 독립적일 것이다. 발사체 발사 후 돌이 풀린 후 스핀 프레임에서 구심력과 코리올리스 힘 모두 돌의 질량과는 독립적인 가속력으로 돌의 모든 부분에 분산된 방식으로 작용한다. 지도 프레임에서 비교했을 때, 해제 후 어떤 힘도 발사체에 작용하지 않는다.

이러한 각각의 경우에 물리적 또는 적절한 가속도는 좌표계 선택뿐만 아니라 물체에 작용하는 물리적 힘에 의해 영향을 받을 수 있기 때문에 좌표 가속도와 다르다. 물리적 힘(직접 접촉이나 정전기 끌어당김과 같은)에 의해 야기되지 않는 좌표 가속도의 구성요소는 (위의 뉴턴 사례와 같이) 다음과 같은 힘(i)으로 귀속된다. (iii) 물체의 모든 온스에 작용하며, (ii) 질량 독립 가속을 유발하며, (iii) 모든 관점에서 존재하지 않는다. 그러한 기하학적(또는 부적절한) 힘에는 코리올리 힘, 오일러 힘, g-강력, 원심력 그리고 (아래에서 보는 바와 같이) 중력 힘도 포함된다.

플랫 스페이스타임 슬라이스에서 보기

일정한 플랫 스페이스타임 슬라이스에서 가속을 조정하기 위한 적절한 가속도의 관계는 민코프스키의 플랫 스페이스 미터법 방정식(cd³)² = (cdt)² - (dx)에 따른다^[6].² 여기서 야드스틱과 동기화된 클럭의 단일 기준 프레임은 각각 지도 위치 x와 지도 시간 t를 정의하고, 여행 물체의 클럭은 적절한 시간 τ을 정의하며, 좌표 평균 무한 변화 앞에 있는 "d"를 정의한다. 이러한 관계는 확장된 지도 프레임이 동시성을 정의하는 관찰자의 유리한 지점에서만 가능하지만 "임의 속도 엔지니어링"의 다양한 문제를 다룰 수 있게 한다.

가속(1+1)D

단방향의 경우 즉, 물체의 가속도가 관찰자의 스페이스타임 슬라이스에서 그 속도에 평행하거나 반타렐일 때, 적절한 가속도 α와 좌표 가속도 a는 로렌츠 계수 γ γ α= througha를³ 통해 관련된다^[7]. 따라서 w=dx/dm의 적절한 속도 변화는 지도 시간 t에 대한 적절한 가속도의 필수 요소다. 상수 α의 경우 Δw=αΔt. 저속에서는 좌표 속도 및 좌표 가속 시간 지도 시간 사이의 잘 알려진 관계(예: Δv=AΔt)로 감소한다.

지속적인 단방향 적정 가속도의 경우, 로렌츠 인자 γ과 이동 거리 Δx 사이뿐만 아니라 빠른 속도 η과 경과된 적정 시간 Δτ 사이에 유사한 관계가 존재한다. 구체적으로 말하면:

${\displaystyle \alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}}}$,

여기서 다양한 속도 매개변수가 다음에 의해 관련된다.

${\displaystyle \eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}}\right)=\pm \cosh ^{-1}\left(\gamma \right)}$.

이 방정식들은 고속에서 가속된 여행의 결과를 설명한다. 예를 들어 "1gee" (10m/s² 또는 연간 약 1.0광년)에서 승객을 목적지까지 절반으로 가속시킨 다음, 나머지 절반 동안 "1gee"로 감속시켜 가능한 최단 시간에 A 지점에서 B 지점까지 지구와 같은 인공 중력을 제공할 수 있는 우주선을 상상해보자.^[8][9] Δx의 지도 거리의 경우,_AB 위의 첫 번째 방정식은 중간점 로렌츠 인자(단위 휴식 값에서 위)를 predicts_mid=1+α(Δx/_AB2)/c로² 예측한다. 따라서 여행자 시계의 왕복 시간은 Δτ = 4(c/α) cosh⁻¹(γ_mid)가 될 것이며, 그 동안 지도 시계에 걸리는 시간은 Δt = 4(c/α) sinh[cosh⁻¹_mid(()가 될 것이다.

이 상상의 우주선은 약 7.1년 동안 지속되는 프록시마 센타우리(지구 시계에서 약 12년), 약 40년 동안 지속되는 은하수의 중앙 블랙홀(지구 시계에서 약 5만4000년 경과), 약 57년(지구 시계에서 500만년 이상 경과)의 안드로메다 은하로의 왕복 여행을 제공할 수 있다. 불행하게도, 오른쪽 그림에 표시된 질량 비율을 시작하기 위한 최대 탑재량으로 설명했듯이, 몇 년 동안 1-지 가속을 유지하는 것은 말하기가 더 쉽다.

애니메이션: 별로 왕복 6.9 리웨이

6.9광년 떨어진 태양(노란색)과 가상의 별(시안) 사이의 적정 가속도(여행자 프레임의 빨간색 화살표)를 일정하게 1gee에서 왕복하는 지도와 여행자의 관점. 태양으로부터 4광년 떨어진 프록시마 센타우리(주황색)는 왼쪽 위쪽으로 주황색으로 표시된다. 각 관점에서 1년은 약 2초마다 또는 100/17.4 프레임마다 경과해야 한다. 이 왕복선박의 각 왕복선박은 지구상에 주둔하고 있는 동료들의 절반밖에 되지 않을 것이다. 이건 시간적 확장이야 다른 차이점으로는 여행자 틀에서 볼 수 있는 공동 움직이는 별들 사이의 거리 변화가 있다. 이것은 작용의 길이 수축이다. 지도 프레임에서 볼 수 있는 좌표 가속도(녹색)는 각 발사 전후 연도에만 의미가 있는 반면, 여행자가 느끼는 적정 가속도(빨간색)는 항해 내내 의미가 크다. 또한 각 발사 지점에서 시작되었지만 발사 후 0.886 맵에서 시작된 광 신호의 흔적도 참고하십시오. 이 맥박은 항해 중간 지점에서 여행자에게 도달하여 감속을 시작하도록 상기시킨다. 지도 틀에서 프록시마 센타우리(Proxima Centauri)는 목적지 별보다 먼저 반전의 맥박을 보지만, 여행자 틀에서는 그 반전이 사실이다. 이것은 행동에서 상대적인 동시성이다. 그럼에도 불구하고 두 관찰자는 시간과 유사한 세계선을 따라 사건의 순서에 동의한다.

곡선 스페이스타임에

일반 상대성 언어에서, 물체의 가속도 4벡터 A(규모가 적절한 가속도)의 구성요소는 적절한 시간에 관한 공변량 파생상품 D를 통한 4-속도 요소와 관련이 있다.

${\displaystyle A^{\lambda }}={\frac {DU^{\lambda }}}}{d\lambda }}}}}{d\lambda }}}}}}}}\ma ^{}{\mu \mu }U^{}{}{}}}}}{{{{{}}}}}}}u }}}}}}}{nu^{nu }}}}}}}{nu }}}}}}$

여기서 U는 물체의 4폭으로 되어 있으며, Ⅱ는 좌표계의 64 연결 계수나 크리스토펠 기호를 나타낸다. 그리스어 첨자는 시간 축의 경우 0, 공간 좌표 축의 경우 1-3 등 4개의 가능한 값을 사용하고 반복 지수를 사용하여 해당 지수의 모든 값에 대한 합계를 표시한다는 점에 유의하십시오. 적절한 가속도가 0인 궤도를 지오데틱스라고 한다.

이 4개의 방정식 집합의 좌측(시간과 3개의 공간과 같은 지수 값에 대해 각각 하나씩)은 객체가 정지해 있는 참조 또는 장부 기록 좌표계의 vantage 지점에서 볼 수 있는 null 시간 구성요소와 결합된 객체의 적절한 가속도 3 벡터다. 오른쪽의 첫 번째 항은 여행자 시계에서 단위 시간 τ 당 물체의 4-속도 U의 시간 유사(에너지/mc) 및 공간 유사(모멘텀/m) 구성요소의 변화 속도를 나열한다.

저속에서는 공간과 같은 구성요소가 좌표 가속도를 나타내기 때문에 오른쪽의 첫 번째 항에 대해 해결합시다. 더 일반적으로, 첫 번째 항이 0이 되면 개체의 좌표 가속도는 0이 된다. 이건...

${\displaystyle {\frac {dU^{\lambda }}{d\tau }}=A^{\lambda }-\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }}$.

따라서 위의 처음 두 애니메이션에서 예시했듯이 좌표 가속은 오른쪽 끝에 있는 연결(또는 기하학적 가속) 용어에 의해 적절한 가속이 정확하게 취소될 때마다 0이 된다.^[10] 주의: 이 용어는 반복 지수 μ와 μ는 허용되는 4개 값의 모든 쌍에 걸쳐 합친 관례에 따라 계산되기 때문에 16개의 개별 속도 및 위치 종속 항의 합계가 될 수 있다.

힘 및 등가성

위의 방정식은 힘과 동등성 원리에 대한 일부 관점도 제공한다. 시간 단위의 시간(초)과 수직 축을 따라 거리 단위의 공간을 설명하기 위해 메트릭(예를 들어 지구 위치 확인 시스템이 정보를 제공하는 것과 같은 로컬 로렌츠 테트라드^[5])에 대한 로컬 장부 좌표를^[4] 고려한다. 만약 우리가 위의 방정식을 여행 물체의 휴식 질량 m으로 곱하고 로렌츠 인자 γ = dt/d³으로 나눈다면, 공간 같은 성분은 측정법을 설명하는 데 사용된 좌표의 관점에서 그 물체에 대한 운동량 변화 속도를 표현한다.

이것은 차례로 가속력과 힘의 적절하고 기하학적인 구성 요소 때문에 부품으로 분해될 수 있다. 시간 유사 성분을 광속 c로 더 곱하고 좌표 속도를 v = dx/dt로 정의하면 에너지 변화율에 대한 표현도 얻을 수 있다.

${\displaystyle {\frac {dE}{dt}}={\vec {v}}\cdot {\frac {d{\vec {p}}}{dt}}}$ (timelike) and ${\displaystyle {\frac {d{\vec {p}}}{dt}}=\Sigma {\vec {f_{o}}}+\Sigma {\vec {f_{g}}}=m$$({\vec{a_{o}}+{\vec {a_{g}}}})($공간적).

여기서 a는_o 적절한 힘에 의한 가속이고 a는_g 기본적으로 우리의 좌표계 선택 때문에 물체에 적용되는 기하학적 가속이다. 저속에서는 이러한 가속도가 결합하여 a=dx²/dt와² 같은 좌표 가속도를 생성하는 반면, 어떤_o 속도에서 단방향 이동의 경우 a의_g 크기는 위의 절에서와 같이 적절한 가속도 α이다³. 일반적으로 이러한 가속도와 힘을 표현하는 것은 복잡할 수 있다.

그럼에도 불구하고 우리가 위의 연결 계수(ECU) 용어를 기하학적 힘의 관점에서 설명하기 위해 이 분류를 사용한다면, 좌표계의 관점에서 물체의 움직임(적어도 저속에서의)은 국소 뉴턴어로 볼 수 있다. 이것은 이미 원심력과 중력을 가진 일반적인 관행이다. 따라서 동등성 원리는 가속 좌표계 및 그 이상으로 뉴턴 법칙의 국부적 유용성을 확장한다.

행성의 표면 거주자

구형 행성이나 항성의 중심에서 고정 반경으로 고정된 저속 관측기의 경우 좌표 가속도_shell a는 a_o by의 적절한 가속도와 거의 관련이 있다.

${\displaystyle {\vec{a}_{shell}={\vec {a}_{o}-{\sqrt {\\frac {r-r_{s}}}{\frac {GM}{r^{2}}}{\hat {r}}}}}}}}}}}}}$

행성이나 별의 슈바르츠실트 반지름 r_s=2GM/c². 우리의 조개관찰자의 반지름이 슈바르츠실트 반지름에 가까워질 때, 행성이나 별의 슈바르츠실트 반지름이 떨어지지 않도록 하기 위해 필요한_o 적절한 가속은 견딜 수 없게 된다.

한편 r>>>r에_s 대해서는 GMm/r만이² 아래쪽으로 가속되는 것을 방지하기 위해 적절한 상승력이 필요하다. 지구 표면에서 이것은 다음과 같이 된다.

${\displaystyle {\vec{a}_{shell}={\vec {a}_{o}-g{\hat{r}}}}$

여기서 g는 중력에 의한 9.8m/s의² 하방 가속도이며,${\displaystyle \stackrel{}{}}r{\displaystyle \stackrel{}{}}$^ ${\$는 중력체 중심에서 방사상으로 바깥쪽으로 향하는 단위 벡터다$$. 따라서 여기서 mg의 외적인 적절한 힘이 아래쪽으로 가속되는 것을 막아야 한다.

4벡터 파생

이 조의 시간 간격 방정식은 단일 계산에서 적절한 가속도와 좌표 가속도 사이의 모든 편차를 다룰 수 있도록 한다. 예를 들어 Christoffel 기호를 계산해 봅시다.^[11]

${\displaystyle \left({\begin{배열}{llll}\left\{\Gamma_{tt}^{t},\Gamma _{tr}^{t},\Gamma _{t\theta}^{t},\Gamma _{t\phi}^{t}\right\}&\left\{\Gamma_{rt}^{t},\Gamma _{rr}^{t},\Gamma _{r\theta}^{t},\Gamma _{r\phi}^{t}\right\}&\left\{\Gamma_{\theta지}^{t},\Gamma _{r\theta}^{t},\Gamma _{\theta\theta}^{t},\Gamma _{\theta \phi}^{t}\right\.}&\left\{\Gamma_{\phi지}^{t},\Gamma _{r\phi}^{t},\Gamma _{\phi \theta}^{t},\Gamma _{\phi \phi}^{t}\right\}\\\left\{\Gamma_{tt}^{r},\Gamma _{tr}^{r},\Gamma _{t\theta}^{r},\Gamma _{t\phi}^{r}\right\}&\left\{\Gamma_{rt}^{r},\Gamma _{rr}^{r},\Gamma _{r\theta}^{r},\Gamma _{r\phi}^{r}\right\}&\left\{\Gamma_{\theta지}^{r},\Gamma _{r\theta}^{r}.,\Gamma _{\theta\theta}^{r},\Gamma _{\theta \phi}^{r}\right\}&\left\{\Gamma_{\phi지}^{r},\Gamma _{r\phi}^{r},\Gamma _{\phi \theta}^{r},\Gamma _{\phi \phi}^{r}\right\}\\\left\{\Gamma_{tt}^{\theta},\Gamma _{tr}^{\theta},\Gamma _{t\theta}^{\theta},\Gamma _{t\phi}^{\theta}\right\}&\left\{\Gamma_{rt}^{\theta},\Gamma _{rr}^{\theta},\Gamm.는 또{r\th에타}^{\theta},\Gamma _{r\phi}^{\theta}\right\}&\left\{\Gamma_{\theta지}^{\theta},\Gamma _{r\theta}^{\theta},\Gamma _{\theta\theta}^{\theta},\Gamma _{\theta \phi}^{\theta}\right\}&\left\{\Gamma_{\phi지}^{\theta},\Gamma _{r\phi}^{\theta},\Gamma _{\phi \theta}^{\theta},\Gamma _{\phi \phi}^{\theta}\right\}\\\left\{\Gamma_{.tt}^{\ph나는};\left\{\Gamma_{rt}^{\phi},\Gamma _{rr}^{\phi},\Gamma _{r\theta}^{\phi},\Gamma _{r\phi}^{\phi}\right\}&\left\{\Gamma_{\theta지}^{\phi},\Gamma _{r\theta}^{\phi},\Gamma _{\theta\theta}^{\phi},\Gamma _{\theta \phi}^{\phi}\right\}&\left\{\Gam _{tr}^{\phi},\Gamma _{t\theta}^{\phi},\Gamma _{t\phi}^{\phi}\right\}및 ,\Gamma.엄마 _{\phi지}^{\phi }}\감마 _{\pi r}^{\pi }}}\감마 _{\phi }^{\phi }{\phi }^{\phi }}}\marray}\rig}\right}}\right}}}}}}}}\rigma _}}}}}}}}}}}}}}\rigma)}}}}}}}}}}}}}}}}}}}}}}}}"$

멀리 조정된 슈바르츠실트 메트릭(c d³)² = (1-r_s/r)(c dt)² - (1-r_s/r)dr² - r dθ²² - (r sin θ)² d d에 대해², 여기서 r은_s 슈바르츠실트 반경 2GM/c이다². 결과적인 계수 배열은 다음과 같다.

${\displaystyle \left({\begin{array}{llll}\left\{0,{\frac {r_{s}}{2r(r-r_{s})}},0,0$\right\}&\left\{{\frac{r_{s}}{2r(r-r_{s})}},0,0,0\right\}&\{0,0,0,0\}&, \ᆯ\\\left\ᆰc^ᆱ(r-r_{s})}{2r^{3}}},0,0,0\right\}&\left\{0,{\frac{r_{s}}{2r(r_{s}-r)}},0,0\right\}&\{0,0,r_{s}-r,0\}&\left\{0,0,0,(r_{s}-r)\sin ^{2}\theta \right\}\\\{0,0,0,0\}&, \left\{0,0,{\frac{1}{r}},0\right\}&\left\{0,{년.frac{1}{r}},0,0\right\}&){0,0,0$,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,{\frac {1}{r}}\right\}&\{0,0,0,\cot(\theta )\}&\left\{0,{\frac {1}{r}},\cot \theta ,0\right\}\end{array}}\right)}$.

이로부터 좌표 가속도를 0으로 설정하여 적절한 가속도를 요구하면 고정 물체의 기하학적 가속을 취소할 수 있다. ${\displaystyle A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,GM/r^{2},0,0\}}$. This does not solve the problem yet, since Schwarzschild coordinates in curved spacetime are book-keeper coordinates^[4] but not those of a local observer. The magnitude of the above proper acceleration 4-vector, namely ${\displaystyle \alpha ={\sqrt {1/(1-r_{s}/r)}}GM/r^{2}}$, is however precisely what we want i.e. the upward frame-invariant proper acceleration needed to counteract the downward geometric acceleration felt by dwellers on the 행성의 표면

위의 Christoffel 기호 세트의 특별한 경우는 위의 r_s 또는 M을 0으로 설정하여 얻은 평면 구면 좌표 세트다.

{0,0,0,1r}{0,0,0, 침대 ⁡ θ}{0,1r, 침대⁡ θ, 0}){\displaystyle \left({\begin{배열}{llll}\left\{0,0,0,0\right\}&, \left\{0,0,0,0\right\}&, \{0,0,0,0\}&, \{0,0,0,0\}\\\left\{0,0,0,0\right\}&, \left\{0,0,0,0\right\}&, \{0,0,-r,0\}&, \left\{0,0,0,-r\sin ^{2}\theta \right\}\\\{0,0,0,0\}&amp을 말한다.\left\{0,0,{\frac{1}{r}},$0\right\}&\left\{0,{\frac {1}{r}},0,0\right\}&\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}&\left\{0,0,0,{\frac {1}{r}}\right\}&\{0,0,0,\cot \theta \}&\left\{0,{\frac {1}{r}},\cot \theta ,0\right\}\end{array}}\right)}$.

이를 통해 for=π/π/2 적도에서 등각 속도 Ω=dφ/dτ로 움직이는 물체의 원심 기하학적 가속을 취소하는 데 필요한 구심적 적정 가속도를 얻을 수 있다. dd/ddr 및 ddr/dr.zero의 경우에 대해 위와 같은 4벡터 합을 형성하면 위에 주어진 회전 운동을 위한 고전적인 가속도에 지나지 않는다. ${\displaystyle A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,-r(d\phi /d\tau )^{2},0,0\}}$ so that a_o=ω²r. 코리올리 효과는 또한 이러한 연결 계수에도 존재하며, 이와 유사하게 좌표-프레임 기하학적으로 발생한다.

참고 항목

• 가속도: 속도 변화
• 적정 속도: 특수 상대성에서의 질량 당 운동량, 4-속도 중 우주와 같은 성분으로 구성된다.
• 적절한 기준 프레임(평평한 스페이스타임): 특수 상대성에서의 가속된 기준 프레임(Minkowski 공간)
• 가공력: 질량 시간 기하급수적인 가속도의 한 가지 이름
• 4벡터: 공간과 시간 사이의 연결을 명시적으로 만들기
• 운동학: 시간에 따라 위치가 변화하는 방법을 연구하기 위해
• 균일 가속도: 좌표 가속도 고정 유지

각주

외부 링크

• Spacetime Physics 초판의 발췌문 및 Edwin F가 게시한 기타 자료. 테일러
• 크리스토펠 상징을 계산하기 위한 매스매티카 프로그램을 포함한 제임스 하틀의 중력책 페이지.
• 앤드류 해밀턴의 노트와 지역 테트라드와 함께 일하기 위한 프로그램들은 볼더 주 콜로라도에 있다.